JAC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7

Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.7

Question 1.
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
Solution:
Let the age of Ani be x years and the age of Biju be y years.
Then, from the given,
x – y = 3 ………….(1)
or y – x = 3 ………(2)
Dharam is twice as old as Ani.
∴ Age of Dharam = 2x years
Biju is twice as old as his sister Cathy. Hence, the age of Cathy is half the age of Biju.
∴ Age of Cathy = \(\frac{y}{2}\) years
Naturally, Dharam is older than Cathy by 30 years.
2x – \(\frac{y}{2}\) = 30
∴ 4x – y = 60 ………..(3)
1. We solve equation (1) and equation (3).
Subtracting equation (1) from equation (3),
we get
(4x – y) – (x – y) = 60 – 3
∴ 3x = 57
∴ x = 19
Substituting x = 19 in equation (1), we get
19 – y = 3
∴ 19 – 3 = y
∴ y = 16
Hence, the age of Ani is 19 years and the age of Biju is 16 years.

2. We now solve equation (2) and equation (3). Adding equations (2) and (3), we get
(y – x) + (4x – y) = 3 + 60
∴ 3x = 63
∴ x = 21
Substituting x = 21 in equation (2), we get
∴ y – 21 = 3
∴ y = 24
Hence, the age of Ani is 21 years and the age of Biju is 24 years.
Thus, the ages of Ani and Biju are 19 years and 16 years respectively or 21 years and 24 years respectively.

Question 2.
One says, “Give me a hundred, friend! I shall then become twice as rich as you.” The other replies, “If you give me ten, I shall be six times as rich as you.” Tell me what is the amount of their (respective) capital? (From the Bijaganita of Bhaskara II) [Hint: x + 100 = 2(y – 100), y + 10 = 6(x – 10)].
Solution:
Let the amount with the first person (say A) be ₹ x and the amount with the second person (say B) be ₹ y.
If B gives ₹ 100 to A. then A will have ₹(x + 100) and B will have ₹(y – 100).
Then, from the first condition, we get
x + 100 = 2(y – 100)
∴ x + 100 = 2y – 200
∴ x – 2y = -300 ………..(1)
If A gives ₹ 10 to B, then A will have ₹(x – 10) and B will have ₹(y + 10).
Then, from the second condition, we get
y + 10 = 6(x – 10)
∴ y + 10 = 6x – 60
∴ 10 + 60 = 6x – y
∴ 6x – y = 70 ………..(2)
Multiplying equation (2) by 2, we get
12x – 2y = 140 ………..(3)
Subtracting equation (1) from equation (3),
we get
(12x – 2y) – (x – 2y) = 140 – (-300)
∴ 11x = 440
∴ x = 40
Substituting x = 40 in equation (1), we get
40 – 2y = -300
∴ 40 + 300 = 2y
∴ 2y = 340
∴ y = 170
Thus, the first person has got ₹ 40 and the second person has got ₹ 170.

Question 3.
A train covered a certain distance at a uniform speed. If the train would have. been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Solution:
Let the regular uniform speed of the train be x km/h and regular time taken by the train be y hours. Then, the total distance of the journey = speed × time = xy km.
Now, according to the first information, the new speed = (x + 10) km/h and new time = (y – 2) hours. Then, speed × time = distance gives
(x + 10) (y – 2) = xy
∴ xy – 2x + 10y – 20 = xy
∴ -2x + 10y = 20 …………..(1)
Again, according to the second condition. the new speed = (x – 10) km/h and new time = (y + 3) hours.
Then, (x – 10) (y + 3) = xy
∴ xy + 3x – 10y – 30 = xy
∴ 3x – 10y = 30 …………..(2)
Adding equations (1) and (2), we get
(-2x + 10y) + (3x – 10y) = 20 + 30
∴ x = 50
Substituting x = 50 in equation (1), we get
-2(50) + 10y = 20
∴ -100 + 10y = 20
∴ 10y = 120
∴ y = 12
Now, the total distance covered by the train = xy = 50 × 12 = 600 km.
Thus, the distance covered by the train is 600 km.

Question 4.
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
Solution:
Let the number of students in each row be x and the number of rows be y. Then total number of students = xy.
From the first condition, number of students in each row = x + 3 and the number of rows = y – 1.
∴ (x + 3)(y – 1) = xy
∴ xy – x + 3y – 3 = xy
∴ -x + 3y = 3 …………..(1)
From the second condition, number of students in each row = x – 3 and the number of rows = y + 2.
∴ (x – 3) (y + 2) = xy
∴ xy + 2x – 3y – 6 = xy
∴ 2x – 3y = 6 ……….. (2)
Adding equations (1) and (2), we get
(-x + 3y) + (2x – 3y) = 3 + 6
∴ x = 9
Substituting x = 9 in equation (1), we get
-9 + 3y = 3
∴ 3y = 12
∴ y = 4
Now, total number of students = xy = 9 × 4 = 36. Thus, the number of students in the class is 36.

Question 5.
In a ΔABC, ∠C = 3∠B = 2 (A + B). Find the three angles.
Solution:
In ΔABC, we have
∠A + ∠B + ∠C = 180°
∴ ∠A + ∠B + 3∠B = 180° (∵ ∠C = 3∠B)
∴ ZA + 4∠B = 180° …………..(1)
Again, ∠A + ∠B + ∠C = 180°
∠A + ∠B + 2(∠A + ∠B) = 180° (∵ ∠C = 2 (∠A + ∠B))
∴ 3(∠A + ∠B) = 180°
∴ ∠A + ∠B = 60° ……….(2)
Subtracting equation (2) from equation (1),
we get
(∠A + 4∠B) – (∠A + ∠B) = 180° – 60°
∴ 3∠B = 120°
∴ ∠B = 40°
Substituting ∠B = 40° in equation (2), we get
∠A + 40° = 60°
∴ ∠A = 20°
Substituting ∠B = 40° in ∠C = 3∠B, we get
∠C = 3(40°)
∴ ∠C = 120°
Thus, in ΔABC, ∠A = 20°; ∠B = 40°; ∠C = 120°
Note: Replacing ∠A + ∠B = \(\frac{\angle \mathrm{C}}{2}\) in ∠A + ∠B + ∠C = 180°, we get a simple equation in one variable is \(\frac{3}{2}\)∠C = 180°.
After solving it for ∠C, ∠B and ∠A can be found easily.

Question 6.
Draw the graphs of the equations 5x – y = 5 and 3x – y = 3. Determine the co-ordinates of the vertices of the triangle formed by these lines and the y-axis.
Solution:
5x – y = 5 gives y = 5x – 5

x	1	2
y	0	5

3x – y = 3 gives y = 3x – 3

x	1	2
y	0	3

Now, we draw the graphs of both the equations.

From the graph, we observe that the co-ordinates of the vertices of the triangle formed by the graphs of 5x – y = 5 and 3x – y = 3 and the y-axis are (1, 0), (0, -3) and (0, -5).

Question 7.
Solve the following pair of linear equations:
1. px + qy = p – q
qx – py = p + q
2. ax + by = c
bx + ay = 1 + c
3. \(\frac{x}{a}-\frac{y}{b}=0\)
ax + by = a² + b²
4. (a – b)x + (a + b) y = a² – 2ab – b²
(a + b) (x + y) = a² + b²
5. 152x – 378y = -74
-378x + 152y = -604
Solution:
1. px + qy = p – q ……….(1)
qx – py = p + q ……….(2)
Multiplying equation (1) by p and equation (2) by q, we get
p²x + pqy = p² -pq ……….(3)
q²x – pqy = pq + q² ……….(4)
Adding equations (3) and (4), we get
(p²x + pqy) + (q²x – pqy) = (p² – pq) + (pq + q²)
∴ x(p² + q²) = p² + q²
∴ x = 1
Substituting x = 1 in equation (1), we get
p(1) + qy = p – q
∴ qy = -q
∴ y = -1
Thus, the solution of the given pair of linear equations is x = 1, y = -1.

2. ax + by = c ……….(1)
bx + ay = 1 + c ……….(2)
Multiplying equation (1) by a and equation (2) by b, we get
a²x + aby = ac ……….(3)
b²x + aby = b + bc ……….(4)
Subtracting equation (4) from equation (3), we get
(a²x + aby) – (b²x + aby) = ac – (b + bc)
x(a² – b²) = ac – b – bc
x = \(\frac{c(a-b)-b}{a^2-b^2}\)
Substituting x = \(\frac{c(a-b)-b}{a^2-b^2}\) in equation (1), we get

Thus, the solution of the given pair of linear equations is
x = \(\frac{c(a-b)-b}{a^2-b^2}\), y = \(\frac{c(a-b)+a}{a^2-b^2}\)

3. \(\frac{x}{a}-\frac{y}{b}=0\) ……….(1)
ax + by = a² + b² ……….(2)
From equation (1), we get
\(\frac{x}{a}=\frac{y}{b}\)
y = \(\frac{b}{a}\)x
Substituting y = \(\frac{b}{a}\)x in equation (2), we get

Substituting x = a in y = \(\frac{b}{a}\)x, we get
y = \(\frac{b}{a}\)(a)
∴ y = b
Thus, the solution of the given pair of linear equations is x = a, y = b.

4. (a – b)x + (a + b)y = a² – 2ab – b² ……….(1)
(a + b) (x + y) = a² + b²
∴ (a + b)x + (a + b)y = a² + b² ……….(2)
Subtracting equation (1) from equation (2), we get
[(a + b)x + (a + b)y] – [(a – b)x + (a + b)y] = (a² + b²) – (a² – 2ab – b²)
∴ x(a + b – a + b) = a² + b² – a² + 2ab + b²
∴ x (2b) = 2ab + 2b²
∴ x = \(\frac{2 b(a+b)}{2 b}\)
∴ x = a + b
Substituting x = a + b in equation (1), we get
(a – b)(a + b) + (a + b)y = a² – 2ab – b²
∴ a² – b² + (a + b) y = a² – 2ab – b²
∴ (a + b)y = -2ab
∴ y = \(-\frac{2 a b}{a+b}\)
Thus, the solution of the given pair of linear equations is x = a + b, y = \(-\frac{2 a b}{a+b}\)

5. 152x – 378y = -74 ……….(1)
-378x + 152y = -604 ……….(2)
Adding equations (1) and (2), we get
-226x – 226y = -678
∴ x + y = 3 (Dividing by -226) ……….(3)
Subtracting equation (2) from equation (1),
we get
(152x – 378y) – (-378x + 152y) = (-74) – (-604)
∴ 530x – 530y = 530
x – y = 1 (Dividing by 530) ……….(4)
Adding equations (3) and (4), we get
2x = 4
∴ x = 2
Substituting x = 2 in equation (3), we get 2 + y = 3
∴ y = 1
Thus, the solution of the given pair of linear equations is x = 2, y = 1.

Question 8.
ABCD is a cyclic quadrilateral (See the given figure). Find the angles of the cyclic quadrilateral.

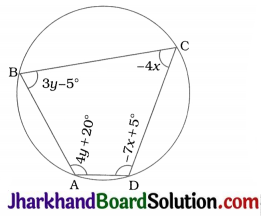
Solution:
ABCD is a cyclic quadrilateral.
∠A + ∠C = 180° and ∠B + ∠D = 180°
∠A + ∠C = 180° gives 4y + 20° – 4x = 180°
∴ 4y – 4x = 160
∴ y – x = 40° (Dividing by 4) …………..(1)
∠B + ∠D = 180° gives 3y – 5° – 7x + 5° = 180°
∴ 3y – 7x = 180° …………..(2)
From equation (1), we get y = x + 40°
Substituting y = x + 40° in equation (2), we get
3(x + 40°) – 7x = 180°
∴ 3x + 120° – 7x = 180°
∴ -4x = 60°
∴ x = -15°
Substituting x = -15° in equation (1), we get
y – (-15) = 40°
∴ y + 15° = 40°
∴ y = 25°
Now, ∠A = 4y + 20° = 4(25°) + 20° = 120°,
∠B = 3y – 5° = 3 (25°) – 5° = 70°,
∠C = -4x = -4(-15) = 60° and
∠D = -7x + 5° = -7(-15°) + 5° = 110°
Thus, in the given cyclic quadrilateral ABCD.
∠A = 120°, ∠B = 70°, ∠C = 60°, ∠D = 110°.