Class 10

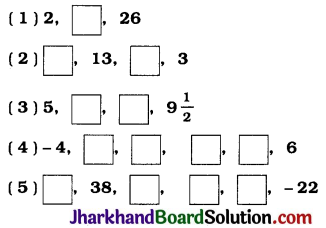
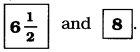Jharkhand Board JAC Class 10 Sanskrit Solutions व्याकरणम् समास: Questions and Answers, Notes Pdf.

JAC Board Class 10th Sanskrit व्याकरणम् समास:

समासशब्दस्य व्युत्पत्तिः – सम् उपसर्गपूर्वकात् असुँ (अस्) धातोः घनि प्रत्यये कृते ‘समासः’ इति शब्दो निष्पद्यते। अस्य अर्थः संक्षिप्तीकरणमिति अस्ति। (‘सम्’ उपसर्गपूर्वक ‘अस्’ धातु से ‘धजि’ प्रत्यय करने पर ‘समास’ शब्द निष्पन्न होता है। इसका अर्थ ‘संक्षिप्तीकरण’ है।)

समासस्य परिभाषा – समसनं समासः अथवा अनेकपदानाम् एकपदीभवनं समासः अर्थात् यदा अनेकपदानि मिलित्वा एकपदं जायन्ते तदा सः समासः इति कथ्यते। यथा – सीतायाः पति = सीतापतिः। अत्र सीतायाः पतिः इति पदद्वयं मिलित्वा एकपदं (सीतापतिः) जातम् अतः अयमेव समासः अस्ति। (संक्षिप्तीकरण समास है अथवा अनेक पदों का एक पद होना समास है। अर्थात् जब अनेक पद मिलकर एक पद निर्मित करते (बनाते) हैं, तब वह समास कहा जाता है। जैसे- सीतायाः पतिः (सीता का पति)= सीतापतिः। यहाँ “सीतायाः पतिः” ये दो पद मिलकर एक पद (सीतापतिः) बना। अत: यह ही समास है।)

समासे जाते अर्थे किमपि परिवर्तनं न भवति। योऽर्थः ‘सीतायाः पतिः’ इत्सस्य विग्रहवाक्यस्य अस्ति सः एव अर्थः ‘सीतापतिः’ इत्यस्य समस्तशब्दस्य अस्ति। (समास बनने पर अर्थ में कोई भी परिवर्तन नहीं होता है जो अर्थ ‘सीतायाः पतिः’ इस विग्रहवाक्य का है वह ही अर्थ ‘सीतापतिः’ इस समस्त शब्द का है।)

पूर्वोत्तरविभक्तिलोपः – सीतायाः पतिः = सीतापतिः। अस्मिन् विग्रहे सीतायाः इत्यत्र षष्ठीविभक्तिः, पतिः इत्यत्र प्रथमाविभक्तिश्च श्रूयेते। समासे कृते अनयोः द्वयोरपि विभक्तयोः लोपो भवति। तत्पश्चात् ‘सीतापति’ इति समस्तशब्दात् पुनरपि प्रथमाविभक्तिः क्रियते इत्येव सर्वत्र अवगन्तव्यम्। (सीतायाः पतिः = सीतापतिः। इस विग्रह में ‘सीतायाः’ इसमें षष्ठी विभक्ति है, ‘पतिः’ इसमें प्रथमाविभक्ति सुनाई देती है। समास करने पर इन दोनों विभक्तियों का लोप होता है। तत्पश्चात् ‘सीतापति’ इस समस्त शब्द से पुनः प्रथमा विभक्ति की जाती है जिसे सभी जगह अर्थात् सम्पूर्ण समस्त शब्द में जानना चाहिए।)

समासयुक्तः शब्दः समस्तपदं कथ्यते। यथा- ‘सीतापतिः’ इति समस्तपदम्। समस्तशब्दस्य अर्थं बोधयितुं यद् वाक्यम् उच्यते तद्वाक्यं विग्रहः इति कथ्यते। यथा सीतायाः पतिः इति वाक्यं विग्रहः अस्ति। (समासयुक्त शब्द समस्त पद कहा जाता है। जैसे ‘सीतापतिः’ यह समस्तपद है। समस्त शब्द का अर्थ जानने के लिए जो वाक्य बोला जाता है वह वाक्य ‘विग्रह’ कहा जाता है। जैसे- ‘सीतायाः पतिः’ यह वाक्य विग्रह है।)

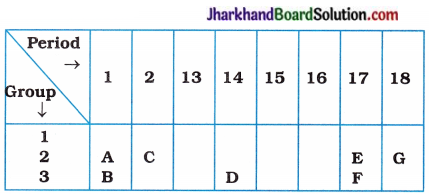
समासस्यभेदाः – संस्कृतभाषायां समासस्य मुख्यरूपेण चत्वारः भेदाः सन्ति। समासे प्रायशः वे पदे भवतः- पूर्वपदम् उत्तरपदम् व। पदस्य अर्थः पदार्थः भवति। यस्य पदार्थस्य प्रधानता भवति तदनुरूपेण एव समासस्य संज्ञा अपि भवति। यथा प्रायेण पूर्वपदार्थप्रधानः अव्ययीभावः भवति। प्रायेण उत्तरपदार्थप्रधानः तत्पुरुषः भवति। तत्पुरुषस्य भेदः कर्मधारयः भवति। कर्मधारस्य भेद द्विगु भवति। प्रायेण अन्यपदार्थप्रधान बहुव्रीहिः भवति। प्रायेण उभयपदार्थप्रधानः द्वन्द्वः भवति। एवं समासस्य सामान्यरूपेण षड्भेदाः भवन्ति। (संस्कृतभाषा में समास के मुख्य रूप से चार भेद हैं। समास में प्राय: दो पद होते हैं पूर्वपद और उत्तरपद। पद का अर्थ पदार्थ होता है। जिस पदार्थ की प्रधानता होती है उसी के अनुसार ही समास की संज्ञा (नाम) भी होती है। जैसे प्रायः पूर्व पदार्थ प्रधान ‘अव्ययीभाव’ होता है। प्रायः उत्तर पदार्थ प्रधान ‘तत्पुरुष’ होता है। तत्पुरुष का भेद कर्मधारय होता है। कर्मधारय का भेद ‘द्विगु’ होता है। प्रायः अन्य पदार्थ प्रधान ‘बहुव्रीहि’ होता है। प्रायः उभयपदार्थ प्रधान ‘द्वन्द्व’ होता है। इस प्रकार सामान्य रूप से समास के छ: भेद होते हैं।)

1. अव्ययीभावसमासः

यदा विभक्ति, समीप-इत्यादिषु अर्थेषु वर्तमानम् अव्ययपदं सुबन्तेन सह नित्यं समस्यते तदा असौ अव्ययीभावसमासो भवति। अथवा इदमत्र अवगन्तव्यम्- (जब विभक्ति, समीप-इत्यादि अर्थों में वर्तमान अव्यय पद सुबन्त के साथ नित्य समास होता है तब यह अव्ययीभाव समास होता है। अथवा इसको इस प्रकार जानना चाहिए-)

1. अस्य समासस्य प्रथमशब्दः अव्ययं द्वितीयश्च संज्ञाशब्दो भवति। (इस समास का प्रथम शब्द अव्यय और द्वितीय संज्ञा शब्द होता है।)
2. अव्ययशब्दार्थस्य अर्थात् पूर्वपदार्थस्य प्रधानता भवति। (अव्यय शब्द के अर्थ की अर्थात् पूर्व पदार्थ की प्रधानता होती है।)
3. समासस्य पदद्वयं मिलित्वा अव्ययं भवति। (समास के दो पद मिलकर अव्यय होता है।)
4. अव्ययीभावसमासः नपुंसकलिङ्गस्य एकवचन भवति। यथा – (अव्ययीभाव समास नपुंसकलिङ्ग के एकवचन में होता है।)
ध्यातव्यम् – (अ) “यथा विभक्ति, समीप-इत्यादिषु” से तात्पर्य है –
1. विभक्ति
2. समीप
3. समृद्धि
4. समृद्धि का नाश
5. अभाव
6. नाश
7. अनुचित
8. शब्द की अभिव्यक्ति
9. पश्चात्
10. यथा
11. क्रमश:
12. एकदम
13. समानता
14. सम्पत्ति
15. सम्पूर्णता
16. अन्त तक।

इन सोलह में वर्तमान अव्यय का सुबन्त के साथ नित्य समास होता है।

(ब) नित्यसमास – प्रायः जिस समास का विग्रह न हो उसे ‘नित्यसमास’ कहते हैं। अथवा प्रायः जिसका अपने पदों से विग्रह नहीं होता अर्थात् जिन शब्दों का समास हुआ हो उन शब्दों के द्वारा जिसका विग्रह न हो, वह ‘नित्यसमास’ होता है।

अन्य उदाहरणानि –

अव्ययपदम् ‘उप’, अव्ययस्यार्थ = समीपम् (प्रथम पद में षष्ठी विभक्ति)

अव्ययपदम् ‘अनु’, अव्ययस्यार्थ = पश्चात्, योग्यम् (प्रथम पद में षष्ठी विभक्ति)

अव्ययपदम् ‘प्रति’, अव्ययस्यार्थ = वीप्सा अर्थे (उत्तर पद को दो बार, प्रथम पद में द्वितीया/सप्तमी विभक्ति)

अव्ययपदम् ‘निर्’, अव्ययस्यार्थ = अभावार्थे (प्रथम पद में षष्ठी विभक्ति)

अव्ययपदम् ‘यथा’, अव्ययस्यार्थ = अनतिक्रम्य

अव्ययपदम् ‘स’, अव्ययस्यार्थ = सहितम् (प्रथम पद में तृतीया विभक्ति)

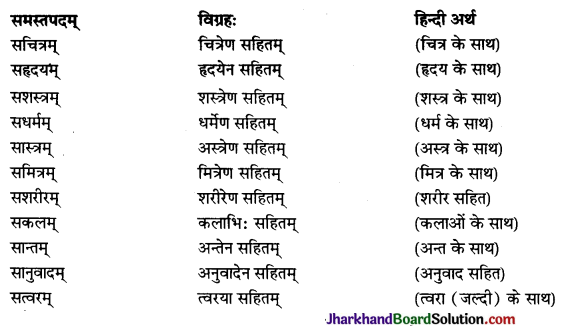
2. कर्मधारयसमासः

यदा तत्पुरुषसमासस्य द्वयोः पदयोः एकविभक्तिः अर्थात् समानविभक्तिः भवति तदा सः समानाधिकरणः तत्पुरुषसमासः कथ्यते। अयमेव समासः कर्मधारयः इति नाम्ना ज्ञायते। अस्मिन् समासे साधारणतया पूर्वपदं विशेषणम् उत्तरपदञ्च विशेष्यं भवति। यथा- नीलम् कमलम् = नीलकमलम्।।

1. अस्मिन् उदाहरणे नीलम् कमलम् इति द्वयोः पदयोः समानविभक्तिः अर्थात् प्रथमा विभक्तिः अस्ति। 2. अत्र नीलम् इति पदं विशेषणम् कमलम् इति पदञ्च विशेष्यम्। अत एव अयं कर्मधारयः समासः अस्ति।

(कर्मधारय समास – जब तत्पुरुष समास के दोनों में एक विभक्ति अर्थात् समान विभक्ति होती है तब वह समानाधिकरण तत्पुरुष समास कहा जाता है। यही समास ‘कर्मधारय’ इस नाम से जाना जाता है। इस समास में साधारणतया पूर्व पद विशेषण और उत्तरपद विशेष्य होता है जैसे-नीलम् कमलम् नीलकमलम्।।

1. इस उदाहरण में “नीलम् कमलम्” इन दो पदों में समान विभक्ति है। अर्थात् प्रथमा विभक्ति है।
2. यहाँ ‘नीलम्’ यह पद विशेषण और ‘कमलम्’ यह पद विशेष्य है। इसलिए यह कर्मधारय समास है।) इसके उदाहरण निम्नलिखित हैं –

1. विशेषण – विशेष्य कर्मधारयः –

2. उपमानोपमेय कर्मधारयः –

3. उपमानोत्तरपद कर्मधारयः –

4. अवधारणपूर्वपद कर्मधारयः –

विशेषणं विशेष्येण समस्यते। अत्र अवधारणार्थं द्योतयितुं विग्रहवाक्ये विशेषणात् परम् ‘एव’ शब्दः प्रयुज्यते।
यथा –

अन्यानि उदाहराणि

3. द्विगु समासः –

1. ‘संख्यापूर्वो द्विगुः’ इति पाणिनीयसूत्रानुसारं यदा कर्मधारयसमासस्य पूर्वपदं संख्यावाची उत्तरपदञ्च संज्ञावाची भवति तदा सः ‘द्विगुसमासः’ कथ्यते।
2. अयं समासः प्रायः समूहार्थे भवति।
3. समस्तपदं सामान्यतया नपुंसकलिङ्गस्य एकवचने अथवा स्त्रीलिङ्गस्य एकवचने भवति।
4. अस्य विग्रहे षष्ठीविभक्तेः प्रयोगः क्रियते। यथा –

द्विगु समास – 1. “संख्यापूर्वो द्विगुः” इस पाणिनीय सूत्रानुसार जब कर्मधारय समास का पूर्वपद संख्यावाची और उत्तरपद संज्ञावाची होता है तब वह द्विगु समास कहा जाता है।
2. यह समास प्रायः समूह के अर्थ में होता है।
3. समस्त पद सामान्यतया नपुंसकलिङ्ग के एकवचन में अथवा स्त्रीलिङ्ग के एकवचन में होता है। 4. इसके विग्रह में षष्ठी विभक्ति का प्रयोग किया जाता है। जैसे –

कुत्रचित् द्विगुसमासः स्त्रीलिङ्गे अपि भवति यथा- (कहीं द्विगु समास स्त्रीलिंग भी होते हैं। जैसे-)

4. बहुव्रीहिसमासः

समासे यदा अन्यपदार्थस्य प्रधानता भवति तदा सः बहुव्रीहिसमासः कथ्यते। अर्थात् अस्मिन् समासे न तु पूर्वपदार्थस्य प्रधानता भवति न हि उत्तरपदार्थस्य प्रत्युतः द्वौ अपि पदार्थो मिलित्वा अन्यपदार्थस्य बोधं कारयतः। समस्तपदस्य प्रयोगः अन्यपदार्थस्य विशेषणरूपेण भवति। यथा – ‘पीतम्’ ‘अम्बर’ यस्य सः= पीताम्बरः (विष्णुः)।
अत्र पीतम् तथा च अम्बरम् इत्यनयोः पदयोः अर्थस्य प्रधानता नास्ति अर्थात् ‘पीला वस्त्र’ इत्यर्थस्य ग्रहणं न भवति प्रत्युत उभौ पदार्थों तु मिलित्वा अन्यपदार्थस्य अर्थात् ‘विष्णुः’ इत्यस्य बोधं कारयतः अर्थात् पीताम्बरः इति समस्तपदस्यार्थः “विष्णुः’ अस्ति अत एव अत्र बहुव्रीहिसमासः अस्ति।
अस्य अन्यानि उदाहरणानि अधोलिखितानि सन्ति। यथा –

(बहुव्रीहिसमास – समास. में जब अन्य पदार्थ की प्रधानता होती है तब वह बहुव्रीहि समास कहा जाता है। अर्थात् इस समास में न तो पूर्व पदार्थ की प्रधानता होती है न ही उत्तर पदार्थ की बल्कि दोनों ही पदार्थ मिलकर अन्य पदार्थ का बोध कराते हैं। समस्त पद का प्रयोग अन्य पदार्थ के विशेषण रूप से होता है। जैसे- ‘पीतम्’ ‘अम्बर’ यस्य सः = पीताम्बरः (विष्णुः)।

यहाँ पर ‘पीतम्’ और वैसे ही ‘अम्बर’ इन पदों के अर्थ की प्रधानता नहीं है अर्थात् ‘पीला वस्त्र’ इस अर्थ का ग्रहण नहीं होता है अपितु दोनों पदार्थ मिलकर अन्य पदार्थ का अर्थात् ‘विष्णुः’ इसका बोध कराते हैं अर्थात् ‘पीताम्बरः’ इस समस्तपद का अर्थ ‘विष्णुः’ है अतः यहाँ बहुव्रीहि समास है।

इसके अन्य उदाहरण निम्नलिखित हैं। जैसे-)

समानाधिकरण-बहुव्रीहिः- यदा समासस्य पूर्वोत्तरपदयोः समानविभक्तिः (प्रथमा विभक्तिः) भवति तदा सः समानाधिकरणबहुव्रीहिः भवति। यथा- (जब समास के पूर्व पद और उत्तरपद में समान विभक्ति (प्रथमा विभक्ति) होती है तब वह समानाधिकरण बहुव्रीहि होता है। जैसे-)

व्यधिकरण-बहुव्रीहिः – यदा समासस्य पूर्वोत्तरपदयोः भिन्न-विभक्तिः भवति तदा सः व्यधिकरणबहुव्रीहिः भवति। यथा-(जब समास के पूर्व पद और उत्तर पद में अलग-अलग विभक्ति होती है तब वह ‘व्यधिकरण बहुव्रीहि’ समास होता है। जैसे-)

तुल्ययोगे बहुव्रीहिः – अत्र सह शब्दस्य तृतीयान्तपदेन सह समासो भवति। यथा –
(तुल्ययोगे बहुव्रीहि- यहाँ ‘सह’ शब्द का तृतीया विभक्ति पद के साथ समास होता है। जैसे-)

1. पुत्रेण सहितः (पुत्र के सहित) = संपुत्रः
2. बान्धवैः सहितः (बन्धुओं के सहित) = सबान्धवः
3. विनयेन सह विद्यानम् (विनय के साथ विद्या को) = सविनयम्
4. आदरेण सह विद्यमानम् (आदर के साथ विद्यमान) = सादरम्
5. पत्या सह वर्तमानः (पत्नी के साथ वर्तमान) = सपत्नीक (वसिष्ठः)

उपमानवाचकबहुव्रीहिः

1. चन्द्रः इव मुखं यस्या सा (चन्द्रमा के समान मुख है जिसका वह (स्त्री)) = चन्द्रमुखी
2. पाषाणवत् हृदयं यस्य सः (पाषाण के समान है हृदय जिसका वह) = पाषाणहृदयः

5. द्वन्द्वसमासः

द्वन्द्वसमासे परस्परं साकांक्षयोः पदयोः मध्ये ‘च’ आगच्छति, अतएव द्वन्द्वसमासः उभयपदार्थप्रधानः भवति। यथा-धर्म: च अर्थ: च-धर्मार्थो। अत्र पूर्वपदं ‘धर्मः’ उत्तरपदम् च ‘अर्थः’, अनयोः द्वयोः अपि प्रधानता अस्ति। द्वन्द्वसमासे समस्तपदं प्रायशः द्विवचने बहुवचने वा भवति। यथा –

(द्वन्द्व समासः – द्वन्द्व समास में परस्पर साभिप्राय पदों के मध्य के ‘च’ आता है; इसलिए द्वन्द्व समास उभयपदार्थ प्रधान होता है। जैसे – “धर्मः च अर्थ: च – धर्मार्थो। यहाँ पूर्व पद ‘धर्म’ और उत्तरपद ‘अर्थ:’ इन दोनों (पदों) की ही प्रधानता है। द्वन्द्व समास में समस्तपद प्रायः द्विवचन अथवा बहुवचन में होता है। जैसे-)

समाहार (समूहः) इत्यस्य अर्थे द्वन्द्वसमासस्य प्रायेण नपुंसकलिङ्ग एकवचनें प्रयोगः भवति। यथा (समाहार (समूह) के अर्थ में द्वन्द्व समास का प्रायः नपुंसकलिङ्ग में प्रयोग होता है। जैसे-)

अन्यानि उदाहरणानि

अभ्यासः

प्रश्न 1.
अधोलिखित प्रश्नानाम् उचित विकल्पं चित्वा लिखत –
1. अव्ययीभावसमासस्य उदाहरणम् अस्ति –
(अ) पीताम्बरः
(ब) नीलकमलम्
(स) यथाशक्ति
(द) त्रिलोकी
उत्तरम् :
(स) यथाशक्ति

2. अव्ययीभाव-समासस्य उदाहरणम् अस्ति –
(अ) महापुरुषः
(ब) चतुर्युगम्
(स) उपकृष्णम्
(द) प्राप्तोदकः
उत्तरम् :
(स) उपकृष्णम्

3. कर्मधारयसमासस्य उदाहरणम् अस्ति –
(अ) पीताम्बरम्
(ब) पीताम्बरः
(स) निर्मक्षिकम्
(द) पञ्चपात्रम्
उत्तरम् :
(अ) पीताम्बरम्

4. द्वन्द्वसमासस्य उदाहरणम् अस्ति –
(अ) दशाननः
(ब) दशपात्रम्
(स) वाक्त्वचम्
(द) महापुरुषः
उत्तरम् :
(स) वाक्त्वचम्

5. ‘सोद्वेगम्’ इति पदस्य विग्रहः स्यात् –
(अ) उद्वेगेन सहितम्
(ब) उद्वेगात् सहितम्
(स) उद्वेगस्य सहित
(द) उद्वेगेन सविधम्
उत्तरम् :
(अ) उद्वेगेन सहितम्

6. ‘दुभिक्षम्’ इति पदस्य विग्रहः अस्ति –
(अ) कष्टेन भिक्षा
(ब) भिक्षायाः अभावः
(स) भिक्षायाः व्यर्द्धिः
(द) न भिक्षा
उत्तरम् :
(ब) भिक्षायाः अभावः

7. ‘सचेष्टम्’ इति पदस्य विग्रहोऽस्ति –
(अ) सद् चेष्टा
(ब) चेष्टया सहितम्
(स) चेष्टायाः समृद्धि
(द) चेष्टोपेतः
उत्तरम् :
(ब) चेष्टया सहितम्

8. ‘प्रत्यक्षम्’ इति पदस्य विग्रहोऽस्ति –
(अ) अक्षम् प्रति
(ब) अक्षम् अक्षम्
(स) अक्षस्य प्रति
(द) अक्षस्य सम्मुखे
उत्तरम् :
(अ) अक्षम् प्रति

9. ‘सहर्षम्’ इति पदस्य विग्रहोऽस्ति –
(अ) हर्षेण सहितम्
(ब) हर्षेण युगपतु
(स) हर्षम् सह
(द) हर्षस्य सहितम्।
उत्तरम् :
(अ) हर्षेण सहितम्

10. ‘रसेन सहितम्’ इति समासविग्रहस्य समस्तपद अस्ति –
(अ) सरसम्
(ब) सहरसम्
(स) सरोसम्
(द) सरस
उत्तरम् :
(अ) सरसम्

11. ‘रथस्य समीपम्’ इति समासविग्रहस्य समस्तपद अस्ति –
(अ) सरथम्
(ब) उपरथम्
(स) रथरयम्
(द) रथोपरि
उत्तरम् :
(ब) उपरथम्

12. “त्रिंशतस्य समीपम्’ इति समासविग्रहस्य समस्तपद अस्ति –
(अ) उपत्रिंशतम्
(ब) सत्रिंशतम्
(स) त्रिंशतम्
(द) अनुत्रिंशतम्
उत्तरम् :
(अ) उपत्रिंशतम्

13. ‘भरणस्य व्यद्धिः’ इति समासविग्रहस्य समस्तपद अस्ति –
(अ) दुर्भरम्
(ब) निर्भरम्
(स) आत्मनिर्भरम्
(द) समनिर्भरम्
उत्तरम् :
(अ) दुर्भरम्

14. ‘दिनं दिनम्’ इति समासविग्रहस्य समस्तपद अस्ति –
(अ) अनुदिनम्
(ब) सुदिनम्
(स) प्रतिदिनम्
(द) दिनंदिनम्
उत्तरम् :
(अ) अनुदिनम्

प्रश्न 2.
प्रदत्तेषु उत्तरेषु यद् उत्तरं शुद्धम् अस्ति, तत् चीयताम् (दिये गये उत्तरों में से जो उत्तर शुद्ध है, उसे चुनिए)।
1. (i) यथासमयं कार्यं कुरु। (समय पर कार्य करो)
(अ) समयेन अनतिक्रम्य
(ब) समयः अनतिक्रम्य
(स) समयम् अनतिक्रम्य
उत्तरम् :
(स) समयम् अनतिक्रम्य।

(ii) सीतारामौ वनम् अगच्छताम्। (सीता और राम वन को गए।)
(अ) सीता च रामः च
(ब) सीते च रामौ च
(स) सीता च रामश्च च
उत्तरम् :
(अ) सीता च रामः च।

(iii) मुनयः कन्दं च मूलं च फलं च खादन्ति। (मुनि कन्द, मूल और फल खाते हैं।)
(अ) कन्दमूलफलानि
(ब) कन्दमूलफलाः
(स) कन्दमूलफलः
उत्तरम् :
(अ) कन्दमूलफलानि।

(iv) स चन्द्रमुखी अस्ति। (वह चन्द्रमुखी है।)
(अ) चन्द्र इव मुखं यस्य सः
(ब) चन्द्र इव मुखं यस्याः सा
(स) चन्द्र इव मुखम्
उत्तरम् :
(ब) चन्द्र इव मुखं यस्याः सा।

2. (i) अतिथे: पाणिपादम् प्रक्षालयति। (अतिथि के हाथ-पैर धोता है।)
(अ) पाणि च पादः च
(ब) पाणिम् च पादम् च
(स) पाणी च पादौ च
उत्तरम् :
(अ) पाणी च पादौ च।

(ii) स प्रतिवर्षम् गङ्गास्नानाय गच्छति। (वह प्रतिवर्ष गंगा-स्नान के लिए जाता है।)
(अ) वर्ष-वर्षम्
(ब) वर्ष:-वर्षः
(स) वर्षे-वर्षे
उत्तरम् :
(अ) वर्ष-वर्षम्।

(ii) सर्वदा असि त्वम्। (सब कुछ देने वाली हो तुम।)
(अ) सर्वं ददाति इति
(ब) सर्व ददाति या सा
(स) सर्वं ददति या सा
उत्तरम् :
(स) सर्वं ददाति या सा।

(iv) उपग्रामं विद्यालयः स्थितः। (गाँव के पास विद्यालय स्थित है।)
(अ) ग्रामस्य समीपम्
(ब) ग्रामं प्रति
(स) ग्रामस्य पश्चात्।
उत्तरम् :
(अ) ग्रामस्य समीपम्।

3. (i) मधुरदुग्धं कस्मै न रोचते ? (मीठा दूध किसको अच्छा नहीं लगता?)
(अ) मधुरं दुग्धं यस्मिन तत्
(ब) मधुरं दुग्धम्
(स) मधुरः दुग्धः
उत्तरम् :
(ब) मधुरं दुग्धम्।

(ii) पितरौ पुत्रस्य उन्नतिं दृष्ट्वा प्रसीदतः। (माता-पिता पुत्र की उन्नति को देखकर प्रसन्न होते हैं।)
(अ) माता च पिता च
(ब) मातरौ च पितरौ च
(स) मातृ च पितृ च
उत्तरम् :
(अ) माता च पिता च।

(iii) पीतम् अम्बरं धारयति। (पीला वस्त्र धारण करता है।)
(अ) पीतम्बरम्
(ब) पीतमाम्बरम्
(स) पीताम्बरम्।
उत्तरम् :
(स) पीताम्बरम्।

(iv) तत्रैका रम्या वाटिका विद्यते। (वहाँ एक रम्य वाटिका है।)
(अ) रम्यावाटिका
(ब) रम्यवाटिका
(स) रम्यं वाटिका
उत्तरम् :
(ब) रम्यवाटिका।

प्रश्न 3.
प्रकोष्ठात् उचितं विकल्पं चित्वा रिक्त स्थानं पूरयत –
1. सैनिका नृपस्य रथस्य पश्चात् ………………….. धावति। (अनुरथम्/प्रतिरथम्)
2. सः नगरस्य समीपे …………………… निवसति। (सनगरम्/उपनगरम्)
3. बालकाय सचित्रम् ……. पुस्तकं रोचते। (चित्रेण सहितम्/चित्रस्य सहितम्)
4. पुण्यः क्षणं क्षणं ……. क्षयति। (प्रतिक्षणम्/अनुक्षणम्)
5. योग्यताम् अनतिक्रम्य …………. कार्यं दीयताम्। (अनुयोग्यताम्/यथायोग्यम्)
उत्तरम् :
1. अनुरथम्
2. उपनगरम्
3. चित्रेण सहितम्
4. प्रतिक्षणम्
5. यथायोग्यम्।

प्रश्न 4.
निम्नलिखितपदानां समासविग्रहः कर्तव्यः –
1. घनश्यामः – ………………
2. प्रतिदिनम् – …………………
3. छत्रोपानहम् – ………………….
4. विद्याधनम् – …………………..
5. अधिहरि –
उत्तरम् :
1. घन इव श्यामः
2. दिनं दिनं प्रति
3. छत्रं च उपाहनम् च
4. विद्या एव धनम्
5. हरौ इति

प्रश्न 5.
निम्नलिखितपदानां समासविग्रहं कृत्वा समासस्य नामापि लेखनीयम् –

उत्तरम् :
1. सुन्दरः बालकः इति (कर्मधारयसमासः)
2. चतुर्णा युगानां समाहारः सा (द्विगुसमासः)
3. पुरुषः व्याघ्रः इव (कर्मधारयसमासः)
4. रूपस्य योग्यम् (अव्ययीभावसमासः)
5. घन इव श्यामः इति (कर्मधारयसमास:)
6. शिरः च ग्रीवा च (द्वन्द्वसमासः)

प्रश्न 6.
निम्नलिखित विग्रह वाक्यानां समासः करणीय –
1. श्वेतं वस्त्रम्
2. मुखं कमलम् इव
3. रूपस्य योग्यम्
4. उन्नतः वृक्षः
उत्तरम् :
1. श्वेतवस्त्रम्
2. कमलमुखम्
3. अनुरूपम्
4. उन्नतवृक्षः

प्रश्न 7.
‘क’- खण्ड ‘ख’- खण्डेन सह योजयत।
क खण्डः – ख खण्डः
1. अव्ययीभावसमासः – उपवनम्
2. द्वन्द्वसमासः – कुसुमकोमलम्
3. कर्मधारयसमासः – हरिहरौ।
उत्तरम् :
क खण्ड – ख खण्ड
1. अव्ययीभावसमासः – उपवनम्
2. द्वन्द्वसमासः – हरिहरौ
3. कर्मधारयसमासः – कुसुमकोमलम्

प्रश्न 8.
अधोलिखित वाक्येषु रेखांकित समस्तपदानां विग्रहं अथवा विग्रह पदानां समासं कृत्वा समासस्य नामपि लिखत –
(i) नीलकमलं विना सर: न शोभते।
(ii) सः प्रतिदिनं देवालयं गच्छति।
(ii) पत्रं च पुष्पं च समर्पयामि।
उत्तरम् :
(i) नील कमलं – नीलं च तत् कमलम् (नीला है जो कमल) (कर्मधारय)
(ii) प्रतिदिनं – दिनं दिनम (दिन-दिन) (अव्ययीभाव)
(iii) पत्रं च पुष्पं च – पत्रपुष्पौ (पत्र-पुष्प) (द्वन्द्व)।

प्रश्न 9.
अधोलिखित वाक्येषु रेखांकित समस्तपदानां विग्रहं अथवा विग्रह पदानां समासं कृत्वा समासस्य नामपि लिखत –
(i) श्रमिकः यथाशक्ति कार्य करोति।
(ii) उद्याने कृष्णसर्प निवसति।
(iii) अत्र शिवः केशवश्च स्तः।
उत्तरम् :
(i) यथाशक्ति – शक्तिम् अनतिक्रम्य (शक्ति के अनुसार) (अव्ययीभाव)
(ii) कृष्णसर्पः – कृष्णः च असौ सर्पः (काला है जो सर्प) (कर्मधारय)
(iii) शिवः केशवश्च – शिवकेशवौ (शिव और केशव) (द्वन्द्व समास)।

प्रश्न 10.
अधोलिखित वाक्येषु रेखांकित समस्तपदानां विग्रहं अथवा विग्रह पदानां समासं कृत्वा समासस्य नामपि लिखत –
(i) मम पुत्रस्य नाम घनश्यामः अस्ति।
(ii) अहं पार्वती च परमेश्वरं वन्दे।
(iii) इदं स्थानं निर्जलम् अस्ति।।
उत्तरम् :
(i) घनश्यामः – घन इव श्यामः (बादल के समान काला) (कर्मधारय)
(ii). पार्वती च परमेश्वरं च – पार्वतीपरमेश्वरौ (पार्वती और शिव) (द्वन्द्व समास)
(iii) निर्जलम् – जलस्य अभाव: (जल का अभाव) (अव्ययीभाव समास)।

प्रश्न 11.
अधोलिखितवाक्येषु स्थूलांकित समस्त पदानां विग्रहम् अथवा विग्रहपदानां समासं कृत्वा समासस्य नामापि लिखत।
1. (i) महानगरमध्ये चलदनिशं कालायसचक्रम्। (महानगर के मध्य दिनरात लौहचक्र चलता है।)
उत्तरम :
महत् च तत् नगरम् (महान् नगर)। कर्मधारय

(ii) दुर्दान्तैर्दशनैरमुना स्थान्नैव जनग्रसनम्। (विकरालै दाँतों द्वारा इससे लोगों का ग्रास न हो।)
उत्तरम् :
दुर्दान्तदशनैः (विकराल दाँत)। कर्मधारय

(iii) कज्जलमलिनं धूमं मुञ्चति। (काजल के समान मैली धुआँ छोड़ती है।)
उत्तरम् :
कज्जलम् इव मलिनम् (काजल की तरह मैली)। कर्मधारय

2. (i) यानानां हि अनन्ताः पंक्तयः। (यानों की अनन्त पंक्तियाँ हैं।)
उत्तरम् :
अनन्तपङ्क्तयः (अनन्त पंक्तियाँ) कर्मधारय

(ii) कुत्सितवस्तु मिश्रितं भक्ष्यम् (भोजन खराब वस्तु-मिश्रित है।)
उत्तरम् :
कुवस्तु (बुरी वस्तु)। कर्मधारय

(iii) समलंधरातलम् (मैला धरातल)।
उत्तरम् :
मलेन सहितम् (मैल सहित)। अव्ययीभाव

3. (i) न हि निर्मलं जलम् (शुद्ध जल नहीं है।)
उत्तरम् :
निर्मलजलम् (शुद्ध जल)। कर्मधारय

(ii) एकान्ते कान्तारे क्षणमपि मे स्यात् सञ्चरणम। (एकान पन में क्षणभर मेरा चलना हो।)
उत्तरम् :
एकान्तकान्तारे (एकान्त वन में)। कर्मधारय

(iii) हरिततरूणां ललितलतानां माला रमणीया। (हरे वृक्षों और सुन्दर लताओं की माला रमणीय है।)
उत्तरम् :
हरितः च असौ तरुः तेषां च। कर्मधारय

4. (i) नवमालिका रसालं मिलिता (नई माल्लिका आम से मिली।)
उत्तरम् :
नवा मालिका (नई माला)। कर्मधारय

(ii) जीवनमरणं नो कामये। (जीना मरना नहीं चाहता)
उत्तरम् :
जीवनम् च मरणम् च। द्वन्द्व

(iii) ततस्तया वृद्धदासी साभिप्रायमवलोकिता। (तब उसने बुढ़िया दासी को सप्रयोजन देखा।)
उत्तरम् :
वृद्धा दासी (बूढ़ी नौकरानी)। कर्मधारय

5. (i) कृष्णाङ्गारान अपि तदर्थिभ्यः प्रेषितवती।
(कोयलों को भी उनके चाहने वालों को भेज दिया।)
उत्तरम् :
कृष्णान् अङ्गाराम् (काले अंगारे)। कर्मधारय

(ii) घृतेनसहितं भोजनं च तस्मै दत्तवती। (घी सहित भोजन उसे दिया।)
उत्तरम् :
सघृतम् (घृत सहित)। अव्ययीभाव

(iii) सव्यवधानं न चारित्रलोपाय।
(रुकावट सहित चरित्र को लोप नहीं करता।)
उत्तरम् :
व्यवधानेन सहितम् (रुकावट सहित)। अव्ययीभाव

6. (i) सूर्यचन्द्रयोः को वा भवतोवरास्य कर्ता ?
(सूर्यचन्द्र में कौनसा आपके वंश का कर्ता है ?)
उत्तरम् :
सूर्यस्य च चन्द्रस्य च/सूर्यः च चन्द्रः च तयोः च। (सूर्य और चन्द्र) द्वन्द्वसमास

(ii) एवम् अधिक्षिपतिनिरनुक्रोशस्य पुत्रौ। (इस प्रकार से फटकारती है- ‘निर्दयी के पुत्रो !)
उत्तरम् :
पुत्रः च पुत्रः च। द्वन्द्व
(i) श्रमक्लम पिपासोष्ण – शीतादीनां सहिष्णुता।
(श्रम की थकावट, प्यास गर्मी शीत आदि की सहनशीलता)
उत्तरम् :
पिपासा च उष्णं च (प्यास और गर्मी) द्वन्द्व

7. (i) वयोरूपगुणैः हीनमपि कुर्यात्सुदर्शनम्।
(आयु रूप गुणों से हीन को भी सुन्दर बनाता है।)
उत्तरम् :
वयः च रूपं च गुणः च तैः च (आयु और रूप और गुणों से) द्वन्द्व

(ii) स च शीते वसन्ते च तेषां पथ्यतमः स्मृतः। द्वन्द्व
(और वह शीत और वसन्त में उनका सबसे अधिक हितकर कहलाता है।)
उत्तरम् :
शीतिवसन्तयोः (सर्दी और वसन्त में) द्वन्द्व

(iii) सर्वेष्वृतुष्वहरहः (सभी ऋतुओं में दिन पर दिन)
उत्तरम् :
अहन् च अहन च। (दिन और दिन) द्वन्द्व

8. (i) सर्वेष्वृतुष्वहरहः (सभी ऋतुओं में)
उत्तरम् :
सर्वऋतुषु। सर्वर्तुषु। (सभी ऋतुओं में) कर्मधारय

(ii) वयोवलशरीराणि देशकालाशनानि च। (आयु-बल-शरीर-देश-काल और भोजन)
उत्तरम् :
देशः च काल: च अशनम् च। (देश और समय और भोजन) द्वन्द्व

(iii) मार्गे गहनकानने सा एकं व्याघ्रं ददर्श। (मार्ग में गहन वन में उसने एक बाघ देखा।)
उत्तरम् :
गहने कानने (गहन वन में) कर्मधारय

9. (i) निजगले बदध्वा चल सत्वरम। (अपने गले में बाँधकर शीघ्र चल)
उत्तरम् :
त्वरेण सहितम् (जल्दी के साथ) अव्ययीभाव

(ii) शृगालेन सहितं पुनरायान्तं ….. (सियार सहित फिर आते हुए को….)
उत्तरम् :
सशृगालम् (सियार सहित) अव्ययीभाव

(ii) बुद्धिर्बलवती तन्वि सर्वकार्येषु सर्वदा। (हे तन्वि ! सभी कार्यों में सदैव बुद्धि बलवती होती है।)
उत्तरम् :
सर्वेषु कार्येषु (सभी कार्यों में) कर्मधारय

10. (i) हयाश्च नागाश्च वहन्ति बोधिता। (घोड़े और हाथी बताने पर वहन करते हैं।)
उत्तरम् :
हयनागाः (घोड़े और हाथी) द्वन्द्व

(ii) अनुक्तमप्यूहति पंडितोजनः। (विद्वान् बिना कहे समझ लेते हैं।)
उत्तरम् :
पण्डितजनः (विद्वान् लोग) कर्मधारय

(iii) यथास्थितः काष्ठगतो हि वह्निः। (जिस प्रकार से काठ में स्थित अग्नि।)
उत्तरम् :
स्थितिम् अनतिक्रम्य। (जिस प्रकार से स्थित) अव्ययीभाव

11. (i) सेवितव्यो महावृक्षः (महावृक्ष की सेवा करनी चाहिए।)
उत्तरम् :
महान् च असौ वृक्षः। (महान् है जो वृक्ष) कर्मधारय

(ii) सम्पत्तौ च विपत्तौ च महतामेकरूपता। (सुख और आपत्ति में महापुरुष समान होते हैं।)
उत्तरम् :
सम्पत्तिविपत्तिषु। (संपत्ति और विपत्ति में)। द्वन्द्व

(iii) धरायाः महत्कम्पनं जातम्। (धरती का महान् कम्पन हो गया।)
उत्तरम् :
महाकम्पनम् (अत्यधिक कम्पन) कर्मधारय

12. (i) बृहत्यः पाषाण शिलाः (बड़ी पत्थर की शिला)
उत्तरम् :
बृहत्पाषाणशिलाः। (बड़ी पत्थर की शिला)। कर्मधारय

(ii) राजानं यथेष्टमभ्यनन्दत् (राजा को इच्छानुसार अभिनन्दन किया।)
उत्तरम् :
इष्टम् अनतिक्रम्य (इच्छानुसार) अव्ययीभाव

(iii) तस्य तारस्वरेण प्रबुद्धाः ग्रामवासिनः। (उसके उच्च स्वर से ग्रामीण जाग गये।)
उत्तरम् :
तारेण स्वरेण (जोर की आवाज से) कर्मधारय

13. (i) हयाश्च नागाश्च वहन्ति बोधिताः (शिक्षित घोड़े और हाथी ढोते हैं।)
उत्तरम् :
हयनागाः (घोड़े और हाथियों) द्वन्द्व समास

14. (i) सः चक्रेण सह गच्छति। (वह चक्र के साथ जाता है।)
उत्तरम् :
सचक्रम् (चक्र के साथ) द्वन्द्व समास

प्रश्न 12.
स्थूलपदेषु समासम् अथवा विग्रहम् कृत्वा उत्तरपुस्तिकायाम् लिखत –
(स्थूलपदों में समास अथवा समास विग्रह करके उत्तर-पुस्तिका में लिखिए।)

1. (i) मधुरवचनम् एव वदेत्। (मधुर वचन ही बोलना चाहिए।)
उत्तरम् :
मधुरम् च तत्
वचनम्। (मधुर है जो वचन।)

(ii) महावीरः सदैव कीर्तिं लभते। (महावीर सदैव कीर्ति को प्राप्त करता है।)
उत्तरम् :
महान् च असौ वीरः। महान् वीरः (महान वीर।)

(ii) सूपकारः भोजनं पचति। (रसोइया भोजन पकाता है।)
उत्तरम् :
सूपं करोति इति। (सूप/दाल बनाता है।)

(iv) रामः मृगस्य पश्चात् धावति। (राम मृग के पीछे दौड़ता है।)
उत्तरम् :
अनुमृगम् (मृग के पीछे।)

2. (i) विद्यालयस्य वार्षिक: महोत्सवः अस्ति। (विद्यालय का वार्षिक महोत्सव है।)
उत्तरम् :
महान् उत्सवः (महान् च असौ उत्सवः च।)

(ii) यथेष्टं भोजनं कुरु। (इच्छित भोजन कर।)
उत्तरम् :
इष्टम् अनतिक्रम्य (इच्छा का अतिक्रमण न करके।)

(iii) सः उन्नतवृक्षम् आरोहति। (वह ऊँचे वृक्ष पर चढ़ता है।)
उत्तरम् :
उन्नतं वृक्षम् (ऊँचा पेड़।)

(iv) कृष्णमेघः वर्षति। (काला बादल बरसता है।)
उत्तरम् :
कृष्णम् मेघम् (काला मेघ।)।

3. (i) छात्रौ किं पठतः ? (दो छात्र क्या पढ़ते हैं ?)
उत्तरम् :
छात्रः च छात्रः च (छात्र और छात्र)।

(i) महापुरुषः येन गतः स पन्थः। (महापुरुष जिससे गया, वही उचित मार्ग है।)
उत्तरम् :
महान् पुरुषः (महान् च असौ पुरुषः।)।

(iii) राधा चतुरा बाला अस्ति। (राधा चतुर बालिका है।)
उत्तरम् :
चतुरबाला (चतुर नारी/बालिका)।

(iv) मधुरवचनं विना भाषणं व्यर्थम् एव अस्ति। (मधुरवचन के बिना भाषण बेकार ही है।)
उत्तरम् :
मधुरम् वचनम् (मीठे वचन)।

4. (i) सा विधिम् अनतिक्रम्य गणितं शिक्षते। (वह विधि का त्याग किए बिना गणित पढ़ाती है।)
उत्तरम् :
यथाविधि (विधि से)।

(i) काकः कृष्णः पिकः कृष्णः को भेदः पिककाकयोः ?
(कौआ काला कोयल काली, कोयलं और कौए में क्या भेद ?)
उत्तरम् :
पिकः च काकः च तयोः। (कोयल और कौआ उनमें)।

(iii) सरोवरे नीलानि कमलानि शोभन्ते। (सरोवर में नीले कमल शोभा देते हैं।)
उत्तरम् :
नील कमलानि। (नीले कमल।)

(iv) राजा अपि नीलोत्पलम् इव चक्षुः उत्पाट्य याचकाय समर्पितवान्।
(राजा ने भी नीलकमल की तरह नेत्र को उखाड़ कर याचक के लिए समर्पित कर दिया।)
उत्तरम् :
नीलम् उत्पलम् इव। (नीले कमल के समान)।

5. (i) सः अपि तत् नेत्रं यथास्थानम् अस्थापयत्।
(उसने भी उस नेत्र को यथास्थान स्थापित कर दिया।)
उत्तरम् :
स्थानम् अनतिक्रम्य। (उचित स्थान पर)।

(i) वृद्धान् उपसेवितुं शीलं यस्य सः राजा याचकाय द्वितीयमपि नेत्रं दत्तवान्।
(वृद्धों की सेवा करने का शील है, जिसका, उस राजा ने याचक के लिए दूसरा नेत्र भी दे दिया।)
उत्तरम् : वृद्धोपसेवी (वृद्धों की सेवा करने वाला)।

(iii) को भेदः पिकः च काकः च तयोः ? (कोयल और कौए में क्या भेद है ?)
उत्तरम् :
पिककाकयोः (कोयल और कौए में)।

(iv) प्रत्येकम् अयनस्य अवधिः षण्मासाः। (प्रत्येक अयन की अवधि छः माह होती है।)
उत्तरम् :
एकम् एकम् (हरेक)।

6. (i) अनेन वचसा प्रतिहतम् अन्तःकरणं यस्य सः अचिन्तयत्। (इस वचन से आहत हुए हृदय वाले उसने सोचा।)
उत्तरम् :
प्रतिहतान्त:करणः (आहत हृदय वाले ने)।

(ii) अनुद्वेगकरं वाक्यं सत्यं प्रियहितं च यत्।
(उद्विग्नता पैदा न करने वाले वाक्य सत्य, प्रिय और हितकर होते हैं।)
उत्तरम् :
प्रियम् हितम् च (प्रिय और हितकर)।

(iii) नीलोत्पलम् इव एकं चक्षुः समर्पितवान्। (नीलकमल की तरह एक नेत्र को सौंप दिया।)
उत्तरम् :
नीलम् उत्पलम्। (नीलकमल)।

(iv) सर्वं ददाति सर्वदाऽस्माकं सन्निधिं क्रियात्। (सब कुछ देती है जो सदा, वह हमारी सन्निधि)
उत्तरम् :
सर्वदा (सब देने वाली)

7. (i) माता च पिता च आगच्छतः। (माता और पिता आते हैं।)
उत्तरम् :
मातापितरौ/पितरौ (माता-पिता)।

(ii) सः पीतम् अम्बरम् धारयति। (वह पीला वस्त्र धारण करता है।)
उत्तरम् :
पीताम्बरम् (पीला वस्त्र)।

(i) नीलकमलम् विना सरः न शोभते। (नीलकमल के बिना सरोवर शोभा नहीं देता।)
उत्तरम् :
नीलम् कमलम् (नीला कमल)।

(iv) त्वं शक्तिम् अनतिक्रम्य परिश्रमं करोषि। (तुम शक्ति के अनुसार परिश्रम करते हो।)
उत्तरम् :
यथाशक्ति (शक्ति के अनुसार)।

8. (i) रामः च लक्ष्मणः च विश्वामित्रस्य शिष्यौ आस्ताम्। (राम और लक्ष्मण विश्वामित्र के शिष्य थे।)
उत्तरम् :
रामलक्ष्मणौ (राम-लक्ष्मण)।।

(ii) अयं संसार: मरणशीलः अस्ति। (यह संसार मरणशील है।)
उत्तरम् :
मरणं शीलं यस्य सः (मरने में ही जिसका शील है।)

(ii) सरोवरे नीलकमलानि शोभन्ते। (सरोवर में नीलकमल शोभा देते हैं।)
उत्तरम् :
नीलानि कमलानिः (नीले कमल)।

(iv) कथमत्र मते च उन्नते च विषमे मार्गे क्रीडथ?
(कैसे यहाँ नीचे और ऊँचे विषम मार्ग में खेल रहे हो?)
उत्तरम् :
नतोन्नते (नीचे-ऊँचे में)

9. (i) दुष्टा बुद्धिः यस्य सः सद्वचनानि तिरस्कृत्य प्राचलत्।
(दुष्ट है बुद्धि जिसकी वह अच्छे वचनों का तिरस्कार करके चल पड़ा।)
उत्तरम् :
दुष्टबुद्धिः (दुष्ट बुद्धि वाला)।

(ii) सर्वेषामेव महत्त्वं विद्यते यथासमयम्। (यथासमय सभी का महत्त्व है।)
उत्तरम् :
समयम् अनतिक्रम्य (समय के अनुसार)।

(ii) ततः युधिष्ठिरार्जुनौ श्रीकृष्णेन सह रथारोहणं नाटयतः।
(तब युधिष्ठिर और अर्जुन श्रीकृष्ण के साथ रथ पर चढ़ने का अभिनय करते हैं।)
उत्तरम् :
युधिष्ठिरः च अर्जुनः च। (युधिष्ठिर और अर्जुन)।

(iv) अये! कथं श्रीकृष्णार्जुनौ युधिष्ठिरश्च। (अरे! कैसे श्रीकृष्ण और अर्जुन और युधिष्ठिर।)
उत्तरम् :
श्रीकृष्णः च अर्जुनः च (श्रीकृष्ण और अर्जुन)।

10. (i) तौ पाणी च पादौ च प्रक्षालयतः। (वे दोनों हाथ और पैर धोते हैं।)
उत्तरम् :
पाणिपादम् (हाथ-पैर)।

(ii) सः प्रतिदिनं दानं करोति स्म। (वह प्रतिदिन दान करता था।)
उत्तरम् :
दिनं दिनम् प्रति (रोजाना)।

(iii) सः प्रजाभ्यः धनधान्यं दातुं दानशाला: अकारयत्।
(उसने प्रजाओं के लिए धन-धान्य देने के लिए दानशालाएँ बनवायीं।)
उत्तरम् :
धनं च धान्यं च (धन और अन्न)

(iv) ततः युधिष्ठिरार्जुनौ श्रीकृष्णेन सह रथारोहणं नाटयतः।
(तब युधिष्ठिर और अर्जुन श्रीकृष्ण के साथ रथारोहण का अभिनय करते हैं।)
उत्तरम् :
युधिष्ठिरः च अर्जुनः च (युधिष्ठिर और अर्जुन)

11. (i) किं चपलबालकेभ्यः भीषणानाम् अस्त्राणाम् प्रदानम् उचितम् ?
(क्या चपल बालकों को भीषण अस्त्रों का देना उचित है ?)
उत्तरम् :
भीषणास्त्राणाम् (भयंकर अस्त्रों का)।

(ii) सर्वेषामेव महत्त्वं विद्यते यथासमयम्। (समय के अनुसार सभी का महत्त्व होता है।)
उत्तरम् :
समयम् अनतिक्रम्य। (समय के अनुसार)।

(iii) नीलमुत्पलं यस्मिन् तत् सरः सुन्दरम्। (नीला कमल है जिसमें, वह तालाब सुन्दर है।)
उत्तरम् :
नीलोत्पलम् (नील कमल वाला)।

प्रश्न 13.
अधोलिखित प्रश्नानाम् उत्तराणि दत्तानि। एतेषु उत्तरेषु समासं समास-विग्रहं वा कृत्वा उत्तरपुस्तिकायां लिखत। (निम्नलिखित प्रश्नों के उत्तर दिए हुए हैं। इन उत्तरों में समास अथवा समास-विग्रह करके उत्तर पुस्तिका में लिखिए।)
1. (i) भगवन् ! किम् उपादेयम् ? (गुरुवचनम्)
(ii) को गुरुः ? (अधिगततत्त्वः)
(iii) अहः च निशा च कः ध्यातव्यः ? (ईश्वरः)
(iv) को पूज्यौ ? (मातापितरौ)
उत्तराणि :
(i) गुरोः वचनम्
(ii) अधिगतं तत्त्वं येन सः
(iii) अहर्निशम्
(iv) माता च पिता च।

2. (i) अत्र केषां वाटिका अस्ति ? (पुष्याणां वाटिका)
(ii) उद्याने मधुर कण्ठेन को कूजतः ? (पिकमयूरी)
(iii) वाटिकायां कीदृशानि पुष्पाणि सन्ति ? (पीतपुष्पाणि)
(iv) अत्र कः वसति ? (पुण्यात्मा)
उत्तराणि :
(i) पुष्पवाटिका
(ii) पिकः च मयूरः च
(iii) पीतानि पुष्पाणि
(iv) पुण्यः आत्मा यस्य सः।

Jharkhand Board JAC Class 10 Science Important Questions Chapter 5 Periodic Classification of Elements Important Questions and Answers.

JAC Board Class 10 Science Important Questions Chapter 5 Periodic Classification of Elements

Additional Questions and Answers

Question 1.
Answer the following questions in short:
(1) From the following elements :
20^Ca, 3^Li, 11^Na, 10^Ne
(a) Select the element which has two shells, both of which are completely filled with electrons.
(b) Select two elements of the same group.
Answer:
(a) Element in which two shells are completely filled with electrons is 10^Ne (2, 8).
(b) Two elements of the same group are 3^Li(2, 1) and 11^Na (2, 8, 1).

(2) Answer the following questions [for an element having atomic number 17] :
(a) Name the element.
(b) In which period will you find this element?
(c) To which group of the periodic table does this element belong?
(d) State the electronic configuration of the element.
Answer:
(a) Chlorine
(b) Third period
(c) Group 17
(d) Electronic configuration : 2, 8, 7

(3) An element X (atomic number 17) reacts with an element Y (atomic number 20) to form a divalent halide.
(a) What is the position of elements X and Y in the periodic table?
(b) What will be the nature of oxide of element Y? Identify the nature of bonding in the compound formed.
Answer:
Element X is a non-metal while element Y is a metal.
Molecular formula of dihalide is YX₂.
(a)

Position	Element X	Element Y
In a group	17	2
In a period	3	4

(b) Basic oxide : YO
Nature of the bond : Ionic

(4) Two elements M and N belong to the same period of the modern periodic table and are in group I and group II respectively. Compare their following properties:
(a) Atomic size
(b) Metallic character
(c) Valency of oxides
(d) Molecular formula of their chlorides
Answer:
(a) Element ‘M’ has larger atomic size than that of ‘N’.
(b) Element ‘M’ possess more metallic? character than that of ‘N’.
(c) Group I : Valency : 1
Group II : Valency : 2
(d) MCl, MCl₂

(5) A part of the periodic table has been shown below :

Answer the following questions on the basis of position of elements in the above table:
(a) Which element is a noble gas? Give reason.
(b) Which element is most electronegative? Give reason.
(c) Write the electronic configuration of B and E.
Answer:
(a Element G is a noble gas, because it is present in group 18 and has zero valency.
(b) Element E is the most electronegative element due to its small size and greater tendency to gain electrons.
(c) Electronic configuration of ‘B’ = 2,8, 1 Electronic configuration of ‘E’ = 2, 7

(6) The positions of elements A, B, C, D, E, F, G and H in their respective groups are as follows :

Group	1	2	13	14	15	16	17	18
Element	A	B	C	D	E	F	G	H

Answer the following questions:
(a) Which elements have the largest and smallest atomic size?
(b) Which elements have the valency 3 and 0 respectively?
Answer:
(a) Largest atomic size : A
Smallest atomic size : G
(b) Valency 3 : Element C
Valency O : Element H

(7) Consider the part of periodic table given below and answer the following questions :

(i) State the most reactive metal.
(ii) How many shells does element d have?
(iii) Identify the element having valency 2.
(iv) Write the number of electrons in the valence shell of j.
(v) Out of h and i, which element is more non-metallic in nature?
(vi) Out of e and h, which element possess large atomic size?
Answer:
(i) d
(ii) 4
(iii) e and g
(iv) 2
(v) h
(vi) e

(8)

Using the above table, answer the following questions:
(i) Which element will form only covalent compounds?
(ii) Which element is a metal with valency 3?
(iii) Which element is a non-metal with valency 3?
(iv) Out of D and E, which one has a bigger atomic size?
(v) Write common name for the family of elements, C and F.
Answer:
(i) E
(ii) D
(iii) B
(iv) D
(v) Inert gases or noble gases

Question 2.
Distinguish between the following :
(1) Elements of a group and Elements of a period
Answer:

Elements of a group	Elements of a period
1. The atomic number of elements increases on moving down the group.	1. The atomic number of elements increases on moving from left to right along a period.
2. All the elements in a group have same number of valence electrons.	2. The number of valence electrons of the elements in a period increases.
3. The chemical reactivity of elements in a group are same or identical.	3. The chemical reactivity of elements in a period are not identical.
4. The atomic radius and metallic character increase on moving down the group.	4. The atomic radius and metallic character decrease on moving from left to right along a period.

(2) Mendeleev’s periodic table and the Modern periodic table
Answer:

Mendeleev’s periodic table	Modern periodic table
1. Mendeleev’s periodic table consists of seven periods and eight groups.	1. Modern periodic table consists of seven periods and eighteen groups.
2. Transition elements are not separated in the Mendeleev’s periodic table.	2. Transition elements are placed in a separate groups in the modern periodic table.
3. In Mendeleev’s periodic table, elements are arranged in increasing order of their atomic masses.	3. In the modern periodic table, elements are arranged in increasing order of their atomic numbers.
4. Period number and group number of an element cannot be predicted.	4. Period number and group number of an element can be determined easily.
5. Mendeleev’s periodic table has descripancies and limitations.	5. Modern periodic table is almost errorless.
6. Periodicity in the properties of elements cannot be explained.	6. Periodicity in the properties of elements can be explained.

(3) Metallic elements and Non-metallic elements
Answer:

Metallic elements	Non-metallic elements
1. They are electropositive elements.	1. They are electronegative elements.
2. Metals have tendency of losing the electrons during the bond formation process.	2. Non-metals have tendency of gaining the electrons during the bond formation process.
3. Oxides of metals are basic.	3. Oxides of non-metals are acidic.
4. Metals possess 1, 2 or 3 electrons in their respective valence shells.	4. Non-metals possess 5, 6 or 7 electrons in their respective valence shells.

Question 3.
Give scientific reasons for the following statements:
(1) Dobereiner’s triads could not arrange all the elements known at that time.
Answer:
In Dobereiner’s triads, three elements were arranged in the order of increasing atomic masses of elements in which the atomic mass of the middle element is the average of the atomic masses of the other two elements.

Dobereiner could identify triads from the elements known at that time was only a coincidence. Thus, this classification of elements into triads could not be applied to all the elements known at that time.

(2) Newlands’ law of octaves could not classify all the elements known at that time.
Answer:
Newlands’ law of octaves was applicable upto calcium. After calcium, every eighth element s did not possess properties similar to that of the first element.

• Newlands’ assumed that only 56 elements existed s in nature.
• Newlands’ law of octaves was found correct only to lighter elements.
• Thus, all the elements could not be classified s by the Newlands’ law of octaves.

(3) No fixed position can be assigned to hydrogen in the periodic table.
Answer:
Electronic configuration of hydrogen resembles with alkali metals.

• Like alkali metals, hydrogen combines with halogens, oxygen and sulphur to form compounds having similar formulae.
• Hydrogen also resembles halogens as it exists in the form of diatomic molecules.
• Hydrogen combines with metals and non-metals to form ionic and covalent bonds respectively.
• Thus, hydrogen cannot be assigned fixed position in the periodic table.

(4) The atomic size decreases in a period on moving from left to right.
Answer:
As moving from left to right in a period, the atomic number of elements increases by 1.

• As atomic number increases, nuclear charge also increases.
• Due to this increased nuclear charge, the electrons are attracted strongly towards the nucleus and hence the atomic size decreases.

(5) On moving down in a group, the atomic radii of elements increases gradually.
Answer:
On moving down in a group, the atomic number of element increases.

• A new shell of electrons is added with increase in atomic numbers of elements.
• Thus, the distance between the valence shell and nucleus increases and atomic size increases down the group inspite of the increase in nuclear charge.

Objective Questions and Answers

Question 1.
Answer the following questions in one word:

1. How many elements are known till date?
2. How many amongst the known elements are naturally occurring?
3. In which two types the elements were classified in early attempts?
4. By which name the law proposed by Dobereiner is known?
5. How many elements were classified by Dobereiner’s triads?
6. Cl, X and I are the elements of Dobereiner’s triad, then what would be the element X?
7. Name the elements Newlands started and ended the classification of elements.
8. With what Newlands’ law of octaves was compared?
9. Name the element having similar property with lithium in Newlands’ law of octaves.
10. Which element possess similar property with boron in Newlands’ law of octaves?
11. Name two elements which were placed in the same slot in Newlands’ octaves.
12. How many elements were known when Mendeleev started the classification of elements?
13. Name two elements which formed compound on which Mendeleev had concentrated.
14. What are the vertical columns and the horizontal rows called in Mendeleev’s periodic table?
15. Which Sanskrit prefix was used by Mendeleev in the naming of elements which were not discovered at that time?
16. Which element was not placed in Mendeleev’s periodic table properly?
17. Which scientist proposed tire ‘periodic law’ for the modern periodic table?
18. Write the number of elements present in first, third and fourth period in the modern periodic table.
19. State the number of elements present in sixth period of the modern periodic table.
20. How many groups are present in the modern periodic table?
21. How many elements exist as gases in the modern periodic table?
22. By what names the elements of group I are known in the modern periodic table?
23. By which formula the maximum number of electrons that can be accommodated in a shell determines?
24. Write the valency of an element having atomic number 13.
25. Name the elements in the modern periodic table having lowest and highest atomic radii.
26. State the radius of a hydrogen atom.

Answer:

1. 118
2. 98
3. Metals and non-metals
4. Law of Triads
5. 9
6. Br
7. Hydrogen and thorium
8. Indian musical notes
9. Sodium
10. Aluminium
11. Cobalt and nickel
12. 63
13. Hydrogen and oxygen
14. Groups and periods
15. Eka
16. Hydrogen
17. Henry Moseley
18. 2, 8, 18
19. 32
20. 18
21. 11
22. Alkali metals
23. 2n²
24. 3
25. He and Fr
26. 39

Question 2.
Define :
(1) Isotopes
Answer:
Atoms of the same element having same atomic number but different atomic masses are known as isotopes.

(2) Periodic properties
Answer:
Properties of the elements which are periodic function of their electronic configuration and are repeated after definite interval of atomic numbers.
OR
Properties which show the regular gradation in the same group (moving from top to bottom) or along a period (moving from left to right) are known as periodic properties.

(3) Valency
Answer:
The valency is the combining capacity of an atom of an element to acquire noble gas configuration.

(4) Atomic radius
Answer:
The distance between the centre of the nucleus and the outermost shell of an isolated atom is called atomic radius.

(5) Metalloids (Semi-metal)
Answer:
Elements which possess intermediate properties of both metals and non-metals are called metalloids or semi-metals.

Question 3.
Fill in the blanks :

1. Lithium, sodium and …………………. are the members of Dobereiner’s triad.
2. Newlands’ law of octaves is applicable for …………………. elements.
3. According to Newlands, …………………. elements occur in nature.
4. Mendeleev named scandium as ………………….
5. The element known as eka-silicon is ………………….
6. The position of cobalt in Mendeleev’s periodic table is prior to ………………….
7. If the valency of an element is 2, then it lies in group ………………….
8. The electronic configuration of an element is 2, 8, 3, then it is an element of …………………. period.
9. In the modern periodic table, noble gases are placed in group ………………….
10. Modern periodic table consists of …………………. periods and …………………. groups.
11. Position of …………………. in the periodic table is controversial.
12. The valency of noble gases is ………………….
13. On moving down in any group, the metallic character of the elements ………………….
14. Oxides of non-metallic elements are …………………. in nature.
15. Oxides of …………………. elements are basic in nature.

Answer:

1. potassium
2. lighter
3. 56
4. eka-boron
5. germanium
6. nickel
7. 2
8. third
9. 18
10. 7, 18
11. hydrogen
12. zero
13. increases
14. acidic
15. metallic

Question 4.
State whether the following statements are true or false:

1. At present, naturally occurring elements are 98.
2. The atomic masses of elements form a Dobereiner’s triad are 14 u, 31 u and 74.9 u respectively.
3. Calcium, strontium and barium form a Dobereiner’s triad.
4. According to the Newlands’ law of octaves, every eighth element had properties similar to that of the first element.
5. Sodium is the eighth element after lithium.
6. Oxygen is the eighth element after sulphur.
7. Phosphorus is tire eighth element after nitrogen.
8. Dobereiner’s triads are observed in Newlands’ octaves.
9. Mendeleev’s periodic law was based on atomic number of element.
10. Molecular formula of oxide of barium is BaO.
11. Mendeleev named gallium for eka-silicon.
12. An element having atomic number 3.5 can be placed between Be and B.
13. There are three valence electrons present in the elements of group I.
14. Electrons are filled in K, L and M shells in the elements of the third period.
15. Each period starts with the filling of electrons in a new shell.

Answer:

1. True
2. False
3. True
4. True
5. True
6. False
7. False
8. True
9. False
10. True
11. False
12. False
13. False
14. True
15. True

Question 5.
Match the following properly :
(1)

Column I	Column II
1. Dobereiner	a. Law of octaves
2. Newlands	b. Periodic law
3. Mendeleev	c. Modern periodic table
4. Henry Moseley	d. Law of triads

Answer:
(1-d), (2-a), (3- b), (4 – c).

(2)

Column I	Column II
1. Li, Na, K	a. Metalloids
2. S, E Cl	b. Noble gases
3. B, Si, Ge	c. Non-metallic elements
4. He, Ne, Ar	d. Metallic elements

Answer:
(1-d), (2-c), (3-a), (4-b).

Question 6.
Draw the following graphs :
1. Draw the graph of Atomic radii → Atomic numbers for the elements of second period.
Answer:

2. Draw the graph of Atomic radii → Atomic numbers for the alkali metal elements.
Answer:

Question 7.
Which one of the following depict the correct representation of atomic radius of an atom?

Answer:
(ii) and (iii)

Question 8.
(A) Choose the correct option from those given below each question:
1. For which of the following element, Mendeleev didn’t left gap in his periodic table?
A. Gallium
B. Beryllium
C. Germanium
D. Scandium
Answer:
B. Beryllium

2. Newlands’ law of octaves was found to be applicable upto …………………
A. nickel
B. cobalt
C. phosphorus
D. calcium
Answer:
D. calcium

3. According to Mendeleev’s periodic law, the elements were arranged in the periodic table in the order of…
A. increasing atomic number.
B. decreasing atomic number.
C. increasing atomic masses.
D. decreasing atomic masses.
Answer:
C. increasing atomic masses.

4. The elements Si, B and Ge are …………………
A. metallic elements
B. non-metals
C. metalloids
D. metal, non-metal and metalloid respectively
Answer:
C. metalloids

5. In Mendeleev’s periodic table, gaps were left for the elements to be discovered later. Which of the following elements found a place in the periodic table later?
A. Be
B. Ge
C. Si
D. Se
Answer:
B. Ge

6. The three imaginary elements X, Y and Z represent a Dobereiner’s triad. If the atomic mass of element X is 14 u and that of element Y is 46 u, then the atomic mass of element Z will be …………………
A. 28
B. 60
C. 78
D. 72
[Hint: According to the law of Dobereiner’s triad,
Atomic mass of Y

Answer:
C. 78

7. The atomic numbers of four elements R Q, R and S are 6, 8, 14 and 16 respectively. Out of these, the element known as metalloid is ……….
A. P
B. Q
C. R
D. S
[Hint: Elements in which generally four? electrons are present in outermost shell are called metalloids.]
Answer:
C. R

8. Which of the following statements is correct with regard to the classification of elements?
A. Elements in modern periodic table are arranged on the basis of increasing atomic masses.
B. Elements in modern periodic table are arranged on the basis of decreasing atomic numbers.
C. In modern periodic table, the element nickel of lower atomic mass is kept before the element cobalt of higher atomic mass.
D. In modern periodic table, the isotopes of chlorine having different atomic masses are kept in the same group.
Answer:
D. In modern periodic table, the isotopes of chlorine having different atomic masses are kept in the same group.

9. Which of the following statements about the modern periodic table is correct?
A. It has 18 horizontal rows known as periods.
B. It has 8 vertical columns known as periods.
C. It has 18 vertical columns known as groups.
D. It has 7 horizontal rows known as groups.
Answer:
B. It has 8 vertical columns known as periods.

10. An element X forms an oxide X₂O₃. In which : group of Mendeleev’s periodic table is this element placed?
A. Group II
B. Group III
C. Group V
D. Group VIII
Answer:
B. Group III

11. Who proposed the ‘Modern periodic law’ for the modern periodic table?
A. Dobereiner
B. Newlands
C. Henry Moseley
D. Mendeleev
Answer:
C. Henry Moseley

12. Which fundamental particle forms the real basis for the modern classification of elements?
A. Proton
B. Electron
C. Neutron
D. Nucleon
Answer:
A. Proton

13. Which of the following is not correct about the trends when going from left to right across the periods of the periodic table?
A. The elements become more non-metallic in nature.
B. The number of valence electrons increases.
C. The atoms lose their electrons easily.
D. The oxides become more acidic.
Answer:
C. The atoms lose their electrons easily.

14. The electronic configuration of the atom of an element X is 2, 8, 4. In modern periodic table, the element X is placed in
A. Group 2
B. Group 14
C. Group 4
D. Group 8
Answer:
B. Group 14

15. The atomic number of an element is 20. In modern periodic table, this element is placed in ……………..
A. 2nd period
B. 3rd period
C. 1st period
D. 4th period
Answer:
D. 4th period

16. The elements A, B, C, D and E have atomic numbers of 2, 3, 7, 10 and 18 respectively. The elements which belong to the same period of the periodic table are
A. A, B, C
B. B, C, D
C. A, D, E
D. B. D, E
Answer:
B. B, C, D

17. The elements A, B, C, D and E have atomic numbers 9, 11, 17, 12 and 13 respectively. The pair of elements which belong to the same group of the periodic table is ……………..
A. A and B
B. B and D
C. D and E
D. A and C
Answer:
D. A and C

18. Which of the following element would lose an electron easily?
A. Mg
B. Na
C. K
D. Ca
Answer:
C. K

19. Which of the following element will gain an electron easily?
A. Na
B. F
C. Mg
D. Al
Answer:
B. F

20. Where would you place the element with electronic configuration 2, 8 in the modern periodic table?
A. Group 8
B. Group 2
C. Group 18
D. Group 10
Answer:
C. Group 18

21. An element which is an essential constituent of all organic compounds belong to ……………..
A. Group 4
B. Group 10
C. Group 16
D. Group 14
Answer:
D. Group 14

22. Which of the following is the valence shell for the elements of second period of the modern periodic table?
A. M-shell
B. K-shell
C. N-shell
D. L-shell
Answer:
D. L-shell

23. The element which has the maximum number of valence electrons is ……………..
A. 15^P
B. 11^Na
C. 14^Si
D. 13^Al
Answer:
A. 15^P

24. The correct increasing order of the atomic radii of the elements oxygen, fluorine and nitrogen is ……………..
A. O, F, N
B. N, F, O
C. O, N, F
D. F, O, N
Answer:
D. F, O, N

25. Which one of the following does not increase while moving down the group of the periodic table?
A. Atomic radius
B. Metallic character
C. Valence electrons
D. Basicity of oxides
Answer:
C. Valence electrons

(B) Choose more than one correct options from those given below each question:
1. Mention the drawbacks of Mendeleev’s periodic table.
A. Position of hydrogen
B. Position of isotopes
C. Arrangement of Noble gases
D. Arrangement of more than one elements in the same slot.
Answer:
A, B, C, D

2. Which of the following increase while moving down the group 17 elements?
A. Atomic radius
B. Valence electrons
C. Metallic character
D. Acidity of oxides
Answer:
A, C

3. Which of the following statements are correct for modern periodic table?
A. New elements can be easily arranged.
B. Predictions of properties of the elements become easy.
C. The elements have been divided into metals and non-metals by the thick zig-zag line running diagonally across the periodic table.
D. Atomic volume of elements decreases on moving down in the group.
Answer:
A, B, C

4. The electronic configuration of the atom of an element is 2, 8, 7. In this reference, which of the following statements are correct?
A. This element belong to group 17.
B. This element has a tendency to gain one electron.
C. This element belongs to fourth period.
D. The element fluorine is placed above this element.
Answer:
A, B, D

(C) In each of the following questions, a statement of Assertion A is given, followed by a Reason R. Read the statements carefully and choose the correct option as under:
A. Assertion A and reason R are true, and reason R is the correct explanation of assertion A.
B. Assertion A and reason R are true, but reason R is not the correct explanation of assertion A.
C. Assertion A is corret but reason R is false.
D. Assertion A is false but reason R is true.
1. Assertion A: The position of hydrogen in modern periodic table is a matter of controversy.
Reason R : The properties of hydrogen resembles with the properties of alkali metals and halogens.
Answer:
A. Assertion A and reason R are true, and reason R is the correct explanation of assertion A.

2. Assertion A: In the modern periodic table, metallic character of elements increases on moving down the group.
Reason R: In the modern periodic table, the elements are arranged in order of their increasing atomic masses.
Answer:
C. Assertion A is corret but reason R is false.

3. Assertion A : Newlands arranged the then known elements in order of musical notes.
Reason R: According to Newlands, proton is responsible for the arrangement of elements in the periodic table.
Answer:
C. Assertion A is corret but reason R is false.

4. Assertion A : Chemical reactivity of the element of group 18 is very less.
Reason R : Their outermost shell is completely filled with electrons.
Answer:
A. Assertion A and reason R are true, and reason R is the correct explanation of assertion A.

Value Based Questions With Answers

Question 1.
Six elements of periodic table A, B, C, D, E and F have atomic numbers of 2, 12, 20, S 18, 4 and 10 respectively (where A, B, C,? D, E and F are not the chemical symbols of s these elements). Based on this information, answer the following questions :
(1) Which of these elements belong to the same groups of the periodic table? Why?
(2) Which of these elements belong to the same periods of the periodic table? Why?
(3) Which of these elements are (i) metals and (ii) non-metals?
(4) Which of these elements are chemically (i) reactive and (ii) unreactive?
(5) What values are indicated in a student in answering the above questions?
Answer:
First of all, write the electronic configurations? of all the given six elements as follows :

Element	Atomic number	Electronic configuration
		K	L	M	N
A	2	2
B	12	2	8	2
C	20	2	8	8	2
D	18	2	2	8
E	4	2	8
F	10	2	8

(1) (i) Elements B, C and E belong to the s group 2 of the periodic table because all of them have an equal number of valence electrons equal to 2.

(ii) Elements A, D and F also belong to the group 18 because they are all inert gases having completely filled outermost electron shells with 8 valence electrons.

(2) (i) Element B (2, 8, 2) and element D (2, 8, 8) belong to the third period because they both have 3 electron shells – K, L and M each.

(ii) Element E (2, 2) and element F (2, 8) belong to the second period because they both have 2 electron shells – K and L each.

(3) (i) Elements B, C and E belonging to group 2 are metals.
(ii) Elements A, D and F belonging to group 18 are non-metals (noble gases).

(4) (i) Elements B, C and E of group 2 are chemically reactive elements.
(ii) Elements A, D and F of group 18 are chemically unreactive elements.

(5) Answering these questions by a student are indicating awareness towards modern periodic classification of the elements and ability to apply his knowledge in solving the related questions.

Question 2.
In his periodic table, Mendeleev arranged all the then known 63 elements in the order of increasing atomic masses in horizontal rows but in such a way that elements having similar properties came directly under one another in the same vertical column. In the classification of the then known elements, Mendeleev was guided mainly by two factors.

In order to make sure that the elements having similar properties fall in the same vertical column, Mendeleev left some gaps in his periodic table. Though leaving gaps in the periodic table was considered to be a drawback of his classification of elements at that time but Mendeleev was firm on his decision.
Answer the following questions:
(1) What are the horizontal rows of Mendeleev’s periodic table known as? How many horizontal rows of elements were there in Mendeleev’s periodic table?

(2) What are the vertical columns of Mendeleev’s periodic table known as? How many vertical columns were there? in Mendeleev’s periodic table?

(3) What were the similar properties used by Mendeleev to classify the then known elements into vertical columns?

(4) What were the two main guiding factors for Mendeleev in the classification of the then known elements?

(5) For what purpose were some gaps left by Mendeleev in his periodic table? Does the modern periodic table also have the 5 gaps left by Mendeleev?

(6) What values were displayed by Mendeleev in presenting his classification of elements?
Answer:
(1) The horizontal rows of elements in the Mendeleev’s periodic table are called periods. There were seven periods in s Mendeleev’s periodic table.

(2) The vertical columns of Mendeleev’s periodic table are called groups. There were eight groups in Mendeleev’s periodic s table.

(3) The similar properties used by Mendeleev to classify the elements into vertical columns were the similar formulae of S their oxides and hydrides.

(4) The two main guiding factors for Mendeleev in the classification of the then known elements were

• increasing t order of atomic masses
• grouping together the elements having similar properties.

(5) These gaps were left for the elements which had not been discovered at that time. He thought that these elements would be discovered later in future. The modern periodic table does not have any gaps.

(6) The various values displayed by Mendeleev were-

• self-confidence
• courage
• foresight
• prophecy.

Question 3.
There are three elements X, Y and Z having atomic numbers of 6, 16 and 19 respectively. Based on this information, Het has been asked to answer the following questions :
(1) In which group of the periodic table would you expect to find (i) element X (ii) element Y and (iii) element Z?
(2) Which two elements will form ionic bonds? Why?
(3) What will be the formula of ionic compound formed?
(4) Which two elements will form covalent bonds? Why?
(5) What will be the formula of covalent compound formed?
(6) What values are displayed by Het in answering the above questions?
Answer:
In order to answer these questions, Het first wrote down the electronic configurations of the elements X, Y and Z by using their atomic numbers, as follows :

Element	Atomic number	Electronic configuration
		K	L	M	N
X	6	2	4
Y	16	2	8	6
Z	19	2	8	8	1

(1) (i) Element X has 4 valence electrons in its atom, so it will be placed in group 4 + 10 = 14 of the modern periodic table.
(ii) Element Y has 6 valence electrons in its atom, so it will be placed in group 6 + 10 = 16 of the modern periodic table.
(iii) Element Z has 1 valence electron in its atom, so it will be placed in group 1 of the modern periodic table.

(2) An ionic bond is formed between a metal element and a non-metal element. Here, the elements Z and Y will combine to form ionic bond.

(3) The element Z has 1 valence electron, so its valency is +1 (after losing this electron). The element Y need two electrons to complete its octet. So, element Y will gain two electrons and form Y^2- ion. Here, two Z⁺ ions will combine with one Y^-2 ion, so that the formula of ionic compound formed will be Z₂Y.

(4) A covalent bond is formed between two non-metallic elements. Here, element X of group 14 is a non-metal and element Y of group 16 is also a non-metal. Therefore, the elements X and Y will combine together to form covalent bonds.

(5) The element X has 4 valence electrons, so its valency is 4. The element Y has 6 valence electrons, so its valency is 2. So, one atom of element X will combine with two atoms of element Y to form a covalent compound having the formula XY₂.

(6) The values displayed by Het in answering these questions are (1) knowledge of modern classification of elements, and (2) understanding of periodic table.

Practical Skill Based Questions With Answers

Question 1.
Complete the following cross-word puzzle :

Across:
(1) An element with atomic number 12.
(3) Metal used in making cans and member of group 14.
(4) A lustrous non-metal which has 7 electrons ; in its outermost shell.

Down:
(2) Highly reactive and soft metal which imparts yellow colour when subjected to flame and is kept in kerosene.
(5) The first element of second period.
(6) An element which is used in making fluorescent bulbs and is second member of group 18 in the modern periodic table.
(7) A radioactive element which is the last member of halogen family.
(8) Metal which is an important constituent of steel and forms rust when exposed to moist air.
(9) The first metalloid in modern periodic table whose fibres are used in making bullet-proof vests.
Answer:

Question 2.
In this ladder, symbols of elements are jumbled up.
(a) Rearrange these symbols of elements in the increasing order of their atomic numbers in the periodic table.
(b) Arrange them in the order of their group also.

Answer:
(a) H, He, Li, Be, B, C, N, O, F, Ne, Na, Mg, Al, Si, E S, Cl, Ar, K, Ca.
(b)

Group	Elements
1	H, Li, Na, K
2	Be, Mg, Ca
13	B, Al
14	C, Si
15	N, P
16	O, S
17	F, Cl
18	He, Ne, Ar

Memory Map

Jharkhand Board JAC Class 10 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.3

Take π = \(\frac{22}{7}\), unless stated otherwise.

Question 1.
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Solution:
R = 4.2, r = 6
Volume of the cylinder = Volume of the melted sphere
πr²h = \(\frac{4}{3}\)πR³
3πr²h = 4πR³
h = \(\frac{4 \pi \mathrm{R}^3}{3 \pi \mathrm{r}^2}\)
= \(\frac{4 \times 4.2 \times 4.2 \times 4.2}{3 \times 6 \times 6}\)
= 4 × 1.4 × 0.7 × 0.7
= 5.6 × 0.49
= 2.744 cm.
Height of the cylinder = 2.74 cm.

Question 2.
Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
Solution:
r₁ = 6 cm, r₂ = 8 cm, r₃ = 10 cm.
Let the radius of the resulting sphere be r cm.
Its volume = \(\frac{4}{3}\)πR³
Volume of the resulting sphere = Volume of the sphere of radius r₁ + Volume of the sphere of radius r₂ + Volume of the sphere of radius r₃

Radius of the resulting sphere = 12 cm.

Question 3.
A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Solution:

Question 4.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4m to form an embankment. Find the height of the embankment.
Solution:
Volume of the earth got by digging the well = πr²h
= \(\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times 14\)
= 99 cm.
R = 1.5 + 4
r = 1.5

Area of the circular embankment around the well = πR² – πr²
= π[(5.5)² – (1.5)²]
= π(5.5 + 1.5) (5.5 – 1.5)
= π(7) (4).

Question 5.
A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Solution:
Volume of ice cream in the cylindrical container =

Alternative Method:
Number of cones will be = \(\frac{\text { Volume of cylinder }}{\text { Volume of cone }}\)
For the cylinder part,
Radius = \(\frac{12}{2}\) = 6 cm, Height = 15 cm
∴ Volume of cylinder = π × r² × h = 540π
For the cone part,
Radius of conical part = \(\frac{6}{2}\) = 3 cm, Height = 12 cm
Radius of hemispherical part = \(\frac{6}{2}\) = 3 cm
Now,
Volume of cone = Volume of conical part + Volume of hemispherical part
\(\left(\frac{1}{3}\right)\) × π × r² × h + \(\left(\frac{2}{3}\right)\) × π × r³
= 36π + 18π
= 54π.
∴ Number of cones = \(\frac{540 \pi}{54 \pi}\) = 10

Question 6.
How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?
Solution:

Question 7.
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Solution:

Volume of sand in the bucket = πr²h
= π × 18 × 18 × 32 cc.
Volume of the conical heap of sand = \(\frac{1}{3}\)πr²h
\(\frac{1}{3}\)πr²h = π × 18 × 18 × 32
πr²h = 3 × π × 18 × 18 × 32
πr² × 24 = 3 × π × 18 × 18 × 32
r² = \(\frac{3 \times \pi \times 18 \times 18 \times 32}{\pi \times 24}\)
r² = 18² × 2²
r = 18 × 2 = \(\frac{72}{2}\) = 36 cm.
l² = h² + r²
= (24)² + (36)²
= (24 × 24) + (36 × 36)
= (2 × 12 × 12 × 2) + (3 × 12 × 12 × 3)
= 12² (4 + 9)
= 12² × 13
l = 12\(\sqrt{13}\) cm.

Question 8.
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Solution:
Quantity of water flowing in the canal in 1 hour = lbh
l = 10 km, b = 6 m, h = 1.5 m
10 × 1000 × 6 × 1.5 cubic metres.
The area this water can irrigate in 1 hour if 8 cm of standing water is needed
= \(\frac{10 \times 1000 \times 6 \times 1.5}{0.08}\)
8 cm = 0.08 mm
Area needed to irrigate in 30 mins. or \(\frac{1}{2}\) hr.

Question 9.
A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
Solution:
d = 20 cm, r = 10 cm = \(\frac{10}{100}\) = 0.1 mt, h = 3 km = 3 × 1000 m.
Volume of water that comes out of the pipe of diameter 20 cm
= πr²h
= π × 0.1 × 0.1 × 3000
= π × 30 cm.
In 1 hr. (60 mins.), volume of water that flows into the tank = π × 30
In 1 minute = \(\frac{\pi \times 30}{60}=\frac{\pi}{2}\) cm.
Volume of the cylindrical tank = πr²h = π × 5 × 5 × 2. d = 10, r = 5
\(\frac{\pi}{2}\) cubic metres of water will be filled in 1 minute
π × 5 × 5 × 2……. \(\frac{\pi \times 5 \times 5 \times 2 \times 2}{\pi}\) = 100 mins.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Exercise 8.1

Question 1.
In ΔABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A, (ii) sin C, cos C.
Solution :

(i) sin A, cos A
AC² = AB² + BC²
= 24² + 7² = 576 + 49
= 625
∴ AC = 25

Question 2.
In the figure, find tan P – cot R.
Solution :

QR² = PR² – PQ² = 13² – 12²
= 169 – 144 = 25.
∴ QR = 5.
tan P = \(\frac{\mathrm{QR}}{\mathrm{PQ}}=\frac{5}{12}\)
cot R = \(\frac{\mathrm{QR}}{\mathrm{QP}}=\frac{5}{12}\)
∴ tan P – cot R = \(\frac{5}{12}=\frac{5}{12}\) = 0

Question 3.
If sin A = \(\frac{3}{4}\), calculate cos A and tan A.
Solution:

Given, sin A = \(\frac{3}{4}\) ⇒ \(\frac{P}{H}\) = \(\frac{3}{4}\)
Let P = 3k and H = 4k.
In right angled ΔABC,
P² + B² = H² (By Pythagoras theorem)
⇒ (3k)² + B² = (4k)²
⇒ 9k² + B² = 16k²
⇒ B² = 16k² – 9k² = 7k²
∴ B = +k\(\sqrt{7}\) (∵ Base cannot be -ve)

Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:

Given, 15 cot A = 8 ⇒ cot A = \(\frac{8}{15}\)
\(\frac{\mathrm{B}}{\mathrm{P}}=\frac{8}{15}\)
B = 8k and P = 15 k
In right angled ΔABC, H² = B² + P² (By Pythagoras theorem)
= (8k)² + (15k)²
= 64k² + 225k²
= 289k²
∴ H = 17k (∵ Side cannot be -ve)
Now, sin A = \(\frac{\mathrm{P}}{\mathrm{H}}=\frac{15 \mathrm{k}}{17 \mathrm{k}}=\frac{15}{17}\)
sec A = \(\frac{\mathrm{H}}{\mathrm{B}}=\frac{17 \mathrm{k}}{8 \mathrm{k}}=\frac{17}{8}\)

Question 5.
Given sec θ = \(\frac{13}{12}\), calculate all other trigonometric ratios.
Solution :

sec θ = \(\frac{1}{cos θ}\)
sec θ . cos θ = 1
\(\frac{13}{12} \times \frac{12}{13}\) = 1
AB² = AC² – BC²
= 13² – 12²
= 169 – 144
= 25
AB = \(\sqrt{25}\) = 5

Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution :

cos A = \(\frac{AC}{AB}\)
cos B = \(\frac{BC}{AB}\)
cos A = cos B
\(\frac{AC}{AB}=\frac{BC}{AB}\)
∴ AC = BC
∴ \(\hat{A}\) = \(\hat{B}\) (∵ Angles opposite to equal sides are also equal)

Question 7.
If cot θ = \(\frac{7}{8}\), evaluate: (i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\) (ii) cot² θ
Solution :

AC² = AB² + BC²
= 7² + 8²
= 49 + 64 = 113
AC = \(\sqrt{113}\)

(ii) cot² θ = (cot θ)²
= (\(\frac{7}{8}\))² = \(\frac{49}{64}\)
Given cot θ = \(\frac{7}{8}\)

Question 8.
If 3 cot A = 4, check whether \(\frac{1-\tan ^2 A}{1+\tan ^2 A}\) = cos² A – sin² A or not.
Solution :

3 cot A = 4
cot A = \(\frac{4}{3}\)
AC² = AB² + BC²
= 4² + 3²
= 16 + 9
= 25
AC = \(\sqrt{25}\) = 5

Question 9.
In triangle ABC, right-angled at B, if tan A = find the value of :
(i) sin A cos C + cos A sin C,
(ii) cos A cos C – sin A sin C.
Solution :
(i) sin A cos C + cos A sin C

(ii) cos A . cos C – sin A . sin C
\(\frac{AB}{AC} \cdot \frac{BC}{AC}\) – \(\frac{BC}{AC} \cdot \frac{AB}{AC}\)

Question 10.
In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:
PR + QR = 25
QR = 25 – PR
PQ² + QR² = PR²
(5)² + (25 – PR)² = PR²
25 + (625 – 50PR + PR²) = PR²
650 – 50PR = PR² – PR² = 0
– 50PR = – 650
PR = \(\frac{-650}{-50}\) = 13.
PR = 13, QR = 25 – PR = 25 – 13 = 12, PQ = 5.

Question 11.
State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = \(\frac{12}{5}\) for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = \(\frac{4}{3}\) for some angle θ.
Solution :
(i) False, because the value of tan A increases from 0 to ∞. Also, tan 45° = 1.
(ii) True, because the value of sec A increases from 1 to ∞.
(iii) False, cos A is the abbreviation used for the cosine of angle A.
(iv) False, because cot A is one symbol. We cannot separate cot and A.
(v) False, because the value of sin θ always lies between 0 and 1. Here, sin θ = \(\frac{4}{3}\) which is greater than 1. So, it is not possible.

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 3 दो चरों वाले रखिक समीकरण का युग्म Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 3 दो चरों वाले रखिक समीकरण का युग्म

लघुत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
एक कक्षा में विद्यार्थियों को पंक्तियों में खड़ा किया जाता है। यदि एक पंक्ति में एक विद्यार्थी को अतिरिक्त खड़ा किया जाए तो पंक्तियों की संख्या 2 कम हो जाती है और यदि एक पंक्ति में एक विद्यार्थी कम खड़ा किया जाय तो पंक्तियों की संख्या 3 बढ़ जाती है। कक्षा कुल विद्यार्थियों की संख्या ज्ञात कीजिए।
हल :
माना कि मूल पंक्तियों की संख्या x है तथा मूलतः प्रत्येक पंक्ति में y विद्यार्थी खड़े किये जाते हैं।
विद्यार्थियों की कुल संख्या = x × y = xy
अब यदि एक पंक्ति में i विद्यार्थी अतिरिक्त खड़ा किया जाये तो एक पंक्ति में विद्यार्थियों की संख्या (y + 1) हो जायेगी तथा दिये गये प्रतिबन्ध से पंक्तियों की संख्या (x – 2) हो जायेगी।
अतः विद्यार्थियों की कुल संख्या
= (y + 1) (x – 2)
∴ (y + 1) (x – 2) = x × y
⇒ xy – 2y + x – 2 = xy
⇒ x – 2y = 2 ……..(1)
पुन: एक पंक्ति में एक विद्यार्थी कम खड़ा किया जाता है तो एक पंक्ति में विद्यार्थियों की संख्या (y – 1) होगी तथा प्रश्न में दिये गये प्रतिबन्ध के अनुसार पंक्तियों की संख्या (x + 3) हो जायेगी।
अतः विद्यार्थियों की कुल संख्या
= (y – 1) (x + 3)
∴ (y – 1) (x + 3) = xy
⇒ xy + 3y – x – 3 = xy
⇒ 3y – x – 3 = 0
⇒ x – 3y = – 3 ……..(2)
समीकरण (1) में से (2) को घटाने पर,

समीकरण (1) में y का मान रखने पर,
x – 2 × 5 = 2
⇒ x = 2 + 10
∴ x = 12
कक्षा में विद्यार्थियों की कुल संख्या = (xy)
= 12 × 5 = 60.

प्रश्न 2.
k का मान ज्ञात कीजिए ताकि निम्न समीकरण युग्म का कोई हल नहीं हो
(3k + 1)x + 3y – 2 = 0
(k² + 1)x + (k – 2)y – 5 = 0
हल :
दिए गए समीकरण युग्म का कोई हल नहीं होने के लिए प्रतिबन्ध

k = – 1 के लिए निम्न वक्तव्य सही है-
\(\frac{3}{k-2}\) ≠ \(\frac{2}{5}\)
अतः दिए गए समीकरण का कोई हल नहीं होगा। यदि k = – 1 है।

प्रश्न 3.
अशोक ने एक टेस्ट में 65 अंक अर्जित किए, जब उसे प्रत्येक सही उत्तर पर 5 अंक मिले तथा प्रत्येक गलत उत्तर पर 2 अंक की कटौती की गई। यदि उसे सही उत्तर पर 3 अंक मिलते तथा प्रत्येक गलत उत्तर पर 1 अंक कटता, तो अशोक 40 अंक अर्जित करता। इस समस्या को बीजगणितीय रूप में व्यक्त कर ग्राफ विधि से हल कीजिए। टेस्ट में कुल कितने प्रश्न थे ?
हल :
माना अशोक द्वारा सही हल किये गये प्रश्नों की संख्या = x
गलत हल किये गये प्रश्नों की संख्या = y
बीज गणितीय निरूपण – पहली शर्त के अनुसार,
⇒ 5x – 2y = 65 …….(1)
दूसरी शर्त के अनुसार,
3x – y = 40 ……………(2)
ज्यामितीय निरुपण – समी. (1) से
5x – 2y = 65
x = \(\frac{65+2 y}{5}\)
y = – 5 रखने पर, x = \(\frac{65-10}{5}=\frac{55}{5}\) = 11
y = 0 रखने पर, x = \(\frac{65-0}{5}=\frac{65}{5}\) = 13
y = 5 रखने पर, x = \(\frac{65+10}{5}=\frac{75}{5}\) = 15
सारणी – I

x	11	13	15
y	-5	0	5

समी. (2) से
3x – y = 40
x = \(\frac{40+y}{3}\)
y = – 7 रखने पर x = \(\frac{40-7}{3}=\frac{33}{3}\) = 11
y = 2 रखने पर x = \(\frac{40+2}{3}=\frac{42}{3}\) = 14
y = 5 रखने पर y = \(\frac{40+5}{3}=\frac{45}{3}\) = 15

सारणी – II

x	11	14	15
y	-7	2	5

आलेख से स्पष्ट है कि दिए गए समीकरण युग्म की दो सरल रेखाऐं बिन्दु (10, 5) पर काटती है।
x = 10, y = 5
टेस्ट में प्रश्नों की संख्या
= 10 + 5 = 15.

प्रश्न 4.
x तथा y के लिए हल कीजिए-
27x + 31y = 85.
31x + 27y = 89.
हल :
दी गयी समीकरणं है-
27x + 31y = 85 ………….(1)
31x + 27y = 89 ………….(2)
समीकरण (1) तथा (2) को जोड़ने पर,

x का मान समीकरण (3) में रखने पर
2 + y = 3
⇒ y = 3 – 2 = 1
अतः x = 2 तथा y = 1 समीकरणों के अद्वितीय हल हैं।

प्रश्न 5.
एक तालाब को दो पाइपों द्वारा भरने में 12 घंटे लगते हैं। यदि बड़े व्यास वाले पाइप को 4 घन्टे तथा छोटे व्यास वाले पाइप को 9 घंटे प्रयोग किया जाता है तो तालाब का आधा भाग भरा जाता है। बताइये कितने समय में तालाब प्रत्येक पाइप द्वारा अलग-अलग भरा जायेगा।
हल :
माना बड़े व्यास वाला पाइप तालाब को x घंटे में तथा छोटे व्यास वाला पाइप y घंटे में भरता है।
∴ बड़े व्यास वाले पाइप द्वारा 1 घंटे में भस गया भाग = \(\frac{1}{x}\)
बड़े व्यास वाले पाइप द्वारा 4 घंटे भरा गया भाग = \(\frac{4}{x}\)
छोटे व्यास वाले पाइप द्वारा 1 घंटे में भरा गया भाग = \(\frac{1}{y}\)
छोटे व्यास वाले पाइप द्वारा 9 घंटे में भरा गया भाग = \(\frac{9}{y}\)
प्रश्नानुसार, \(\frac{4}{x}=\frac{9}{y}\) = \(\frac{1}{2}\) ……….(1)
और यदि दोनों पाइपों से तालाब 12 घंटे में भरा जाता है।
∴ \(\frac{12}{x}=\frac{12}{y}\) = 1 ……….(2)
माना कि \(\frac{1}{x}\) = a तथा \(\frac{1}{y}\) = b यह मान समीकरण (1) तथा (2) में रखने पर
4a + 9b = \(\frac{1}{2}\) ……….(3)
12a + 12b = 1 ……….(4)
समीकरण (3) को 3 से गुणा करके इसमें से समीकरण (4) को घटाने पर

अतः बड़े व्यास वाला पाइप 20 घन्टे तथा छोटे व्यास वाला पाइप 30 घंटे लेगा।

प्रश्न 6.
7 रबड़ और 5 पेन्सिलों का कुल मूल्य ₹ 58 है, जबकि 5 रबड़ और 6 पेन्सिलों का कुल मूल्य ₹ 56 है। इस समस्या को बीजगणितीय रूप में व्यक्त कर ग्राफ विधि से हल कीजिए ।
हल :
माना 1 रबड़ का मूल्य ₹ x तथा एक पेन्सिल का मूल्य ₹ y है।
प्रश्नानुसार,
∴ 7x + 5y = 58
तथा 5 रबड़ और 6 पेन्सिलों का कुल मूल्य = ₹ 56
⇒ 7x + 5y = 56
बीजगणितीय निरूपण
7x + 5y = 58 ……(1)
5x + 6y = 56 …….(2)
ज्यामितीय निरूपण:
समीकरण (1) से,
7x + 5y = 58
⇒ 5y = 58 – 7x
⇒ y = \(\frac{58-7 x}{5}\)
x = 4 रखने पर, y = \(\frac{58-7 \times 4}{5}=\frac{58-28}{5}\) = 6
x = – 1 रखने पर y = \(\frac{58-7 \times(-1)}{5}=\frac{58+7}{5}\) = 13
सारणी – I

x	11	13
y	-5	0

समीकरण (2) से
5x + 6y = 56
⇒ 6у = 56 – 5x
⇒ y = \(\frac{56-5 x}{6}\)
x = – 2 रखने पर, y = \(\frac{56-5 \times(-2)}{6}=\frac{56+10}{6}\)
y = 11
x = 4 रखने पर y = \(\frac{56-5 \times 4}{6}=\frac{56-20}{6}\) = 6

सारणी – II

x	11	13
y	-5	0

सारणी I और सारणी II से प्राप्त x और y के मानों का आलेखन करने पर हमें निम्न आलेख प्राप्त होता है।

आलेख से स्पष्ट है कि दोनों रैखिक समीकरणों से प्राप्त सरल रेखाएँ बिन्दु P(4, 6) पर प्रतिच्छेदित होती हैं।
∴ x = 4 तथा y = 6
अतः एक रबड़ का मूल्य = ₹ 4 तथा एक पेन्सिल का मूल्य = ₹ 6

प्रश्न 7.
अभ्यास पुस्तिका और 3 पेन्सिलों का कुल मूल्य 17 रूपए है, जबकि 3 अभ्यास पुस्तिका और 4 पेन्सिलों का कुल मूल्य 24 रूपए है। इस समस्या को बीजगणितीय रूप में व्यक्त कर ग्राफ विधि से हल कीजिए।
हल :
माना एक अभ्यास पुस्तिका का मूल्य ₹ x तथा एक पेन्सिल का मूल्य ₹ y है।
प्रश्नानुसार,
2 अभ्यास पुस्तिका और 3 पेन्सिलों का मूल्य = ₹ 17
⇒ 2x + 3y = 17
3 अभ्यास पुस्तिका और 4 पेन्सिलों का मूल्य 3x + 4y = ₹ 24
⇒ 3x + 4y = 24
बीजगणितीय निरूपण :
2x + 3y = 17 …….(1)
3x + 4y = 24 …….(2)
ज्यामितीय निरूपण :
समीकरण (1) से,
2x + 3y = 17
⇒ 3y = 17 – 2x
⇒ y = \(\frac{17-2 x}{3}\)
x = 1 रखने पर, y = \(\frac{17-2 \times 1}{3}=\frac{15}{3}\) = 5
x = 4 रखने पर, y = \(\frac{17-2 \times 4}{3}=\frac{9}{3}\) = 3
x = 7 रखने पर, y = \(\frac{17-2 \times 57}{3}=\frac{3}{3}\) = 1
सारणी – I

x	11	13	15
y	-5	0	5

समीकरण (2) से,
3x + 4y = 24
⇒ 4y = 24 – 3x
⇒ y = \(\frac{24-3 x}{4}\)
x = 0 रखने पर y = \(\frac{24-3 \times 0}{4}=\frac{24}{4}\) = 6
x = 4 रखने पर y = \(\frac{24-3 \times 4}{4}=\frac{12}{4}\) = 3
x = 8 रखने पर y = \(\frac{24-3 \times 8}{4}=\frac{0}{4}\) = 0

सारणी – II

x	11	13	15
y	-5	0	5

सारणी I और सारणी II से प्राप्त x और y के मानों का आलेखन करने पर हमें निम्न आलेख प्राप्त होता है :

आलेख से स्पष्ट है कि दोनों रैखिक समीकरणों से प्राप्त सरल रेखाएँ बिन्दु (4, 3) पर प्रतिच्छेद करती हैं।
∴ x = 4 तथा y = 3
अतः एक पुस्तिका का मूल्य = ₹ 4
तथा एक पेन्सिल का मूल्य = ₹ 3

प्रश्न 8.
एक रेलगाड़ी एक निश्चित दूरी एक समान चाल से तय करती है। यदि यह रेलगाड़ी 6 किमी / घंटा तेज चाल से चलती तो यह निश्चित समय से 4 घंटे कम लेती तथा यदि 6 किमी / घंटा धीमी चाल से चलती तो यह निश्चित समय से 6 घंटे अधिक लेती। यात्रा की निश्चित दूरी ज्ञात कीजिए।
हल :
माना रेलगाड़ी की चाल x किमी / घंटा तथा लिया गया समय y घंटे हैं।
∴ रेलगाड़ी द्वारा तय की गई दूरी = चाल × समय = x × y = xy किमी
तेज चलने पर रेलगाड़ी की चाल = (x + 6) किमी / घंटा
रेलगाड़ी द्वारा लिया गया समय = (y – 4) घंटे
अब, दूरी = (x + 6) (y – 4)
⇒ xy = xy – 4x + 6y – 24
⇒ 4x – 6y = – 24 ………..(1)
धीमी गति से चलने पर रेलगाड़ी की चाल = (x – 6) किमी / घंटा
समय = (y + 6) घंटे
अब, दूरी = चाल × समय
⇒ xy = (x – 6) × (y + 6)
⇒ xy = xy + 6x – 6y – 36
⇒ – 6x + 6y = – 36 ………..(2)
समीकरण (1) और समीकरण (2) को जोड़ने पर

समीकरण (1) में x = 30 रखने पर
4 × 30 – 6y = 24
⇒ – 6y = – 24 – 120
⇒ y = \(\frac{-144}{-6}\) = 24
अत: रेलगाड़ी की चाल = 30 किमी / घंटा
रेलगाड़ी द्वारा लिया गया समय = 24 घंटे
तथा रेलगाड़ी द्वारा तय की गई दूरी = 30 × 24
= 720 किमी

प्रश्न 9.
दो संपूरक कोणों में से बड़े कोण का मान छोटे कोण के मान से 18° अधिक है। दोनों कणों के मान ज्ञात कीजिए ।
हल :
माना दिए गए कोण A तथा B हैं।
दिए है,
∠A = ∠B + 18° ………(i)
∵ ∠A व B संपूरक कोण हैं,
∴ ∠A + ∠B = 180°
[∵ संपूरक कोणों का योग 180° होता है]
समीकरण (i) से,
∠B + 18° + ∠B = 180°
2∠B = 162°
∠B = 81°
∴ अभीष्ठ ∠A = 81° + 18° = 99°
अतः अभीष्ट कोण 99° तथा 81° होगे।

प्रश्न 10.
सुमित की आयु उसके बेटे की आयु की तीन गुनी है। पाँच वर्षा के बाद, उसकी आयु अपने बेटे की आयु की ढ़ाई गुना हो जाएगी। इस समय सुमित की आयु कितने वर्ष है?
हल :
माना सुमित की वर्तमान आयु x वर्ष तथा उसके पुत्र की वर्तमान आयु y वर्ष है।
प्रश्नानुसार, x = 3y ………(i)
पाँच वर्ष बाद, सुमीत की आयु = (x + 5)
पाँच वर्ष बाद, पुत्र की आयु = (y + 5)
प्रश्नानुसार, x + 5 = 2\(\frac{1}{2}\)(y + 5) …………(ii)
समीकरण (i) का मान समीकरण (ii) में रखने पर,
3y + 5 = \(\frac{5}{2}\)(y + 5)
3y + 5 = \(\frac{5y}{2}=\frac{25}{2}\)
3y – \(\frac{5y}{2}\) = \(\frac{25}{2}\) – 5
\(\frac{6 y-5 y}{2}=\frac{25-10}{2}\)
\(\frac{y}{2}=\frac{15}{2}\)
समीकरण (i) से,
y = 15 वर्ष
x = 3 × 15 = 45 वर्ष
अतः सुमित की वर्तमान आयु 45 वर्ष तथा उसके पुत्र की वर्तमान आयु 15 वर्ष है।

प्रश्न 11.
एक पिता की आयु अपने दो बच्चों की आयु के योग के तीन गुने के समान है। 5 वर्ष के पश्चात् उसकी आयु बच्चों की आयु के योग के दुगुने के समान होगी। पिता की वर्तमान आयु ज्ञात कीजिए।
हल :
माना, पिता की वर्तमान आयु x वर्ष है तथा उसके दोनों बच्चों की वर्तमान आयु का योग y वर्ष है।
प्रश्नानुसार,
x = 3y …………….(i)
पाँच वर्ष बाद, पिता की आयु = x + 5
पाँच वर्ष बाद पुत्रों की आयु = (y + 5 + 5)
प्रश्नानुसर,
x + 5 = 2 (y + 5 + 5)
x + 5 = 2 ( y + 10 ) …………(ii)
x = 3y, समीकरण (ii) में रखने पर,
3y + 5 = 2y + 20
y = 15 वर्ष
अब, y = 15 समीकरण (i) में रखने पर,
x = 3 × 15
x = 45 वर्ष
अतः पिता की वर्तमान आयु 45 वर्ष है।

प्रश्न 12.
एक भिन्न \(\frac{1}{3}\) हो जाती है, अब उसके अंश से 2 घटाया जाता है, और \(\frac{1}{2}\) वह हो जाती है, जब हर में से 1 घटाया जाए। वह भिन्न ज्ञात कीजिए।
हल :
मान कि भिन्न \(\frac{x}{y}\) है
प्रश्नानुसार, \(\frac{x-2}{y}\) = \(\frac{1}{3}\) …………(i)
तथा \(\frac{x}{y-1}\) = \(\frac{1}{2}\)
⇒ 2x = y – 1
⇒ 2x + 1 = y …………(ii)
समीकरण (i) में y = 2x + 1, रखने पर,
\(\frac{x-2}{2 x+1}=\frac{1}{3}\)
3x – 6 = 2x + 1
x = 7
अब, समीकरण (ii) में x = 7 रखने पर,
y = 2 × 7 + 1
y = 15
अतः अभीष्ट भिन्न \(\frac{7}{15}\) है।

प्रश्न 13.
5 पेंसिलों तथा 7 पेनों का कुल मूल्य ₹ 250 है जबकि 7 पेंसिलों तथा 5 पेनों का कुल मूल्य ₹ 302 है। एक पेंसिल तथा एक पेन का मूल्य ज्ञात कीजिए।
हल :
माना एक पेंसिल का मूल्य ₹ तथा एक पेन का मूल्य ₹ y है।
प्रश्नानुसार,
5x + 7y = 250 ……..(1)
7x + 5y = 302 ………(2)
समीकरण (1) को 5 से तथा समीकरण (2) को 7 से गुणा करने पर
25x + 35y = 1250 ……..(3)
49x + 35y = 2114 ……..(4)
समीकरण (4) में समीकरण (3) घटाने पर

समीकरण (1) में x = 36 रखने पर,
5 × 36 + 7y = 250
7y = 250 – 180
y = \(\frac{70}{7}\) = 10
अत: एक पेंसिल का मूल्य = ₹ 36
तथा एक पेन का मूल्य = ₹ 10

प्रश्न 14.
निम्नलिखित समीकरण युग्म को व्रज-गुणन विधि से हल कीजिए:
x – 3y – 7 = 0
3x – 5y – 15 = 0
हल :
दिया गया समीकरण युग्म
x – 3y – 7 = 0
3x – 5y – 15 = 0
व्रज गुणन विधि से,

तथा \(\frac{y}{-6}=\frac{1}{4}\) ⇒ y = \(\frac{-6}{4}=\frac{-3}{2}\)
अत: x = \(\frac{5}{2}\) और y = \(\frac{-3}{2}\)

प्रश्न 15.
दो संख्याओं का अन्तर 26 है तथा बड़ी संख्या, छोटी संख्या के तीन गुने से 4 अधिक है। संख्याएँ ज्ञात कीजिए।
हल :
माना दो संख्याएँ x और y हैं। यहाँ x > y है।
प्रश्नानुसार x – y = 26 ………(i)
तथा x = 3y +4 ………..(ii)
समीकरण (ii) x = 3y + 4 समीकरण (i) में रखने पर
3y + 4 – y = 26
⇒ 2y = 26 – 4
⇒ y = \(\frac{22}{2}\) = 11
समीकरण (i) में y = 11 रखने पर,
x – 11 = 26
⇒ x = 26 + 11 = 37
अत: संख्याएँ 37 और 11 हैं।

प्रश्न 16.
x और y के मान ज्ञात कीजिए :
\(\frac{2}{x}+\frac{3}{y}\) = 13
\(\frac{5}{x}-\frac{4}{y}\) = – 2
हल :
माना \(\frac{1}{x}\) = a तथा \(\frac{1}{y}\) = b, तब दिए गए समीकरण निम्न प्रकार से होगे :
2a + 3b = 13 …………(i)
5a – 4b = – 2 …………(ii)
समीकरण (i) को 4 से तथा (ii) को उसे गुणा करके जोड़ने पर,
8a + 12b = 52
15a – 12b = – 6
23a = 46
⇒ a = \(\frac{46}{23}\) = 2
समीकरण (i) में a = 2 रखने पर,
2 × 2 + 3b = 13
⇒ 3b = 13 – 4 = 9
⇒ b = \(\frac{9}{3}\) = 3
अब a = \(\frac{1}{x}\) ⇒ \(\frac{1}{x}\) = 2 ⇒ x = \(\frac{1}{2}\)
और b = \(\frac{1}{y}\) ⇒ \(\frac{1}{y}\) = 3 ⇒ y = \(\frac{1}{3}\)
अतः x = \(\frac{1}{2}\) तथा y = \(\frac{1}{3}\)

प्रश्न 17.
k के किन मानों (किस मान) के लिए निम्न समीकरणों के युग्म का एक अद्वितीय हल है :
x + 2y = 5 और 3x + ky + 15 = 0
हल :
दिया है, समीकरण युग्मः
x + 2y = 5
और 3x + ky + 15 = 0
दिए गए समीकरणों के युग्म की समीकरणों a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से तुलना करने पर,
a₁ = 1, b₁ = 2, c = – 5, a₂ = 3, b₂ = k, c₂ = 15
∵ दिए गए युग्म का एक अद्वितीय हल है,
∴ \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\)
अर्थात् \(\frac{1}{3}\) ≠ \(\frac{2}{k}\)
k ≠ 6
अत: 6 के अतिरिक्त, k के प्रत्येक मान के लिए दिए हुए समीकरणों के युग्म का एक अद्वितीय हल होगा।

प्रश्न 18.
c का मान कीजिए, यदि समीकरण निकाय cx + 3y + (3 – c) = 0, 12x + cy – c = 0 के अपरिमित रूप से अनेक हल हैं।
हल :
दिए गए समीकरण हैं :
cx + 3y + (3 – c) = 0
तथा 12x + cy – c = 0
दिए गए समीकरण युग्म की समीकरण युग्म a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से तुलना करने पर,
a₁ = c, b₁ = 3, c₁ = 3 – c
तथा a₂ = 12, b₂ = c, c₂ = – c
रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होने के लिए शर्त:

प्रश्न 19.
K का मान ज्ञात कीजिए यदि समीकरण निकाय 2x + 3y = 7, (k + 1) x + (2k – 1) y = 4k + 1 के अपरिमित रूप से अनेक हल हैं।
हल :
दिए गए समीकरणों का निकाय है:
2x + 3y = 7
तथा (k + 1) x + (2k – 1)y = 4k + 1
जहाँ, a₁ = 2, b₁ = 3, तथा c₁ = – 7
और a₂ = (k + 1), b₂ = (2k – 1) तथा c₂ = – (4k + 1)
रैखिक समीकरणों के युग्म के अपरिमित रूप में अनेक हल होने के लिए शर्त

⇒ 4k – 2 = 3k + 3
4k – 3k = 3 + 2
k = 5
तथा 12k + 3 = 14k – 7
12k – 14k = – 7 – 3
– 2k = – 10
k = 5
अतः k = 5 है।

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क)

1. दो चरों वाले रैखिक समीकरण का आलेख सदैव एक ………………. रेखा को निरूपित करता है।
2. वह समीकरण युग्म जिसका हल अद्वितीय होता है, रैखिक समीकरणों का ………….. युग्म कहलाता है।
3. वह समीकरण युग्म जिसका कोई हल नहीं है, रैखिक समीकरणों का ………………… युग्म कहलाता है।
4. k का वह मान जिसके लिए समीकरण निकाय x + 2y = 3 तथा 5x + ky = 7 का कोई हल नहीं है, है ……………..
5. ………………… विधि में दोनों समीकरणों के दो चरों में से एक चर के गुणांक के समान करके विलुप्त कर दूसरे चर का मान ज्ञात करते हैं।

हल :

1. सरल,
2. संगत,
3. असंगत,
4. 10 या ± \(\frac{14}{3}\)
5. विलोपन

निम्न कथनों में सत्य / असत्य बताइए :

प्रश्न (ख)

1. दो चरों वाले रैखिक समीकरण का आलेख सदैव एक सरल रेखा को निरूपित करता है।
2. x और y के मानों से सम्बद्ध कोई भी युग्म जो दोनों समीकरणों को सन्तुष्ट करता हो, युग्म का शून्यक कहलाता है।
3. प्रतिच्छेदी रेखाओं के अनन्त हल होते हैं।
4. संपाती रेखाओं का केवल एक हल होता है।
5. समांतर रेखाओं का निकाय असंगत होता है।

हल :

1. सत्य,
2. सत्य,
3. असत्य,
4. असत्य,
5. सत्य

(ग) बहुविकल्पीय प्रश्न :

प्रश्न 1.
k का वह मान जिसके लिए समीकरण निकाय x + y – 4 = 0 तथा 2x + ky = 3 का कोई हल नहीं है, है:
(A) – 2
(B) ≠ 2
(C) 3
(D) 2
हल :
दिया है, निकाय का कोई हल नहीं है।

अत: सही विकल्प (D) है।

प्रश्न 2.
K का वह मान जिनके लिए रैखिक समीकरण युग्म kx + y = k² तथा x + ky = 1 के अपरिमित रूप से अनेक हल हैं, है:
(A) ± 1
(B) 1
(C) – 1
(D) 2
हल :
अपरिमित रूप से अनेक हल के लिए शर्त :

अतः सही विकल्प (A) है।

प्रश्न 3.
k का वहमान जिसके लिए रैखिक समीकरण निकाय x + 2y = 3, 5x + ky + 7 = 0 असंगत है, है :
(A) \(\frac{-14}{3}\)
(B) \(\frac{2}{5}\)
(C) 5
(D) 10
हल :
रैखिक समीकरण निकाय के लिए अंसगत होने के लिए शर्त्त :

अत: सही विकल्प (D) है।

प्रश्न 4.
रैखिक समीकरणों y = 0 तथा y = – 6 के युग्म का एक:
(A) अद्वितीय हल है
(B) कोई हल नहीं है
(C) अनेक हल हैं
(D) सिर्फ एक हल (0, 0) है
हल :
सही विकल्प (B) है।

प्रश्न 5.
रैखिक समीकरणों \(\frac{3 x}{2}+\frac{5 y}{3}\) = 7 तथा 9x + 10y = 10 का युग्म :
(A) संगत है
(B) असंगत है
(C) संगत है तथा सिर्फ एक हल है।
(D) संगत है तथा अनेक हल हैं
हल :

अतः सही विकल्प (B) है।

प्रश्न 6.
k का मान जिसके लिए समीकरण 3x – y + 8 = 0 तथा 6x + ky = – 16 संपाती रेखाओं को व्यक्त करें, है:
(A) –\(\frac{1}{2}\)
(B) \(\frac{1}{2}\)
(C) 2
(D) – 2
हल :
∵ संपाती रेखाओं के लिए शर्त :

अत: सही विकल्प (D) है।

प्रश्न 7.
यदि रैखिक समीकरणों का कोई युग्म संगत हो, तो इसके आलेख की रेखाएँ होंगी :
(A) समांतर
(B) सदैव संपाती
(C) प्रतिच्छेदी या संपाती
(D) सदैव प्रतिच्छेदी
हल :
सही विकल्प (C) है।

प्रश्न 8.
समीकरण x = a और y = b का युग्म आलेखीय रूप से वे रेखाएँ निरूपित करता है, जो :
(A) समांतर हैं-
(B) (b, a) पर प्रतिच्छेद करती हैं।
(C) संपाती हैं
(D) (a, b) पर प्रतिच्छेद करती हैं
हल :
सही विकल्प (D) हैं।

प्रश्न 9.
आश्रित रैखिक समीकरणों के युग्म का एक समीकरण – 5x + 7 = 2 है। दूसरा समीकरण हो सकता है –
(A) 10x + 14y + 4 = 0
(B) – 10x – 14y + 4 = 0
(C) – 10x + 14y + 4 = 0
(D) 10x – 14y = – 4
हल :
सही विकल्प (D) है।

प्रश्न 10.
मेरी आयु पुत्र की आयु की तिगुनी है। 13 वर्ष बाद मेरी आयु पुत्र की आयु की दुगुनी रह जाएगी। मेरी और मेरे पुत्र की आयु बताइए-
(A) 39 वर्ष, 13 वर्ष
(B) 45 वर्ष, 15 वर्ष
(C) 30 वर्ष, 10 वर्ष
(D) 36 वर्ष, 12 वर्ष ।
हल :
मान लीजिए मेरी आयु (वर्षो में) x और मेरे पुत्र की आयु (वर्षो में) y है ।
प्रश्नानुसार, x = 3y ⇒ x – 3y = 0 … (i)
और x + 13 = 2(y + 13)
अर्थात् x – 2y = 26 – 13
⇒ x – 2y – 13 = 0
वज्रगुणन द्वारा समी. (i) व (ii) को हल करने पर

अर्थात् मेरी आयु 39 वर्ष और मेरे पुत्र की आयु 13 वर्ष है।
अत: सही विकल्प (A) है।

प्रश्न 11.
दो अंकों वाली संख्या के अंकों का योगफल 7 है। अंकों का क्रम उलट देने पर प्राप्त संख्या पहली संख्या से 9 अधिक है। वह संख्या ज्ञात कीजिए :
(A) 43
(B) 34
(C) 52
(D) 25
हल :
मान लीजिए दी हुई संख्या में दहाई अंक x और इकाई अंक y है। तब
दी हुई संख्या = 10x + y
अंकों का क्रम उलटने पर संख्या = 10y + x
प्रश्नानुसार, x + y = 7 ⇒ x + y – 7 = 0 ………….(i)
और (10x + y) + 9 = 10y + x
और 9x – 9y + 9 = 0
या x – y + 1 = 0 ……(ii)
समी. (i) व (ii) को वज्रगुणन द्वारा हल करने पर,

अतः अभीष्ट संख्या = 10x + y = 10 × 3 + 4 = 30 + 4 = 34 है।
सही विकल्प (B) है।

प्रश्न 12.
एक लड़के की आयु अभी अपनी माता की आयु की एक तिहाई है। यदि माता की वर्तमान आयु x वर्ष है तो 12 वर्ष बाद लड़के की आयु होगी :
(A) \(\frac{x}{3}\) + 12
(B) \(\frac{x+12}{3}\)
(C) x + 4
(D) \(\frac{x}{3}\) – 12
हल :
यहाँ माता की वर्तमान आयु = x वर्ष
माना पुत्र की वर्तमान आयु = y वर्ष
लेकिन प्रश्नानुसार, y = x × \(\frac{1}{3}\)
y = \(\frac{x}{3}\)
पुत्र की 12 वर्ष पश्चात् आयु = (y + 12) वर्ष
y = \(\frac{x}{3}\) रखने पर
अतः 12 वर्ष बाद लड़के की आयु = \(\frac{x}{3}\) + 12
सही विकल्प (A) है।

प्रश्न 13.
C के किस मान के लिए समीकरण युग्म Cx – y = 2 तथा 6x – 2y = 3 के अनन्त हल हैं:
(A) 3
(B) – 3
(C) – 12
(D) कोई मान नहीं
हल :
समीकरण युग्म को निम्न प्रकार लिखा जा सकता है :
Cx – y – 2 = 0 ……………(i)
तथा 6x – 2y – 3 = 0 ……………(ii)
समीकरण युग्म के अनन्त हल के लिए प्रतिबन्ध

अत: विकल्प (D) सही है।

प्रश्न 14.
k के किस मान के लिए समीकरण युग्म 4x – 3y = 9, 2x + ky = 11 का कोई हल नहीं है-
(A) \(\frac{9}{11}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{-3}{2}\)
(D) \(\frac{-2}{3}\)
हल :
दिया गया समीकरण युग्म है :
4x – 3y – 9 = 0, 2x + ky – 11 = 0
कोई हल न होने के लिए प्रतिबन्ध

⇒ k = \(\frac{-3}{2}\) या k ≠ \(\frac{-11}{3}\)
अतः k = \(\frac{-3}{2}\)
अत: सही विकल्प (C) है।

प्रश्न 15.
यदि समीकरणों 5x + 2y = 16 और 3x + \(\frac{6}{5}\)y = 2 का हल होगा :
(A) संगत
(B) असंगत
(C) दोनों (A) और (B)
(D) इनमें से कोई नहीं।
हल :
दिए गए समीकरण युग्म की निम्न प्रकार से भी लिख सकते हैं-
5x + 2y – 16 = 0 ……….(i)
15x + 6y – 10 = 0 ……….(ii)

अतः दिए गए समीकरण युग्म का कोई हल नहीं है। दिया गया समीकरण युग्म असंगत है ।
सही विकल्प (B) है।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Exercise 8.4

Question 1.
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution :
(i) We know that, cosec²A = 1 + cot² A ⇒ cosec A = \(\sqrt{1+\cot ^2 \mathrm{~A}}\)

Question 2.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution :
(i) sin A sin² A + cos² A = 1
sin² A = 1 – cos² A

Question 3.
Evaluate:
(i) \(\frac{\sin ^2 63^{\circ}+\sin ^2 27^{\circ}}{\cos ^2 17^{\circ}+\cos ^2 73^{\circ}}\)
(ii) sin 25° cos 65° + cos 25° sin 65°.
Solution :
(i) \(\frac{\sin ^2 63^{\circ}+\sin ^2 27^{\circ}}{\cos ^2 17^{\circ}+\cos ^2 73^{\circ}}\)
sin (90 – θ) = cos θ
sin (90 – 27°) = cos 27°
sin 63° = cos 27°
sin² 63 = cos² 27°

cos (90 – θ) = sin θ
cos (90° – 73°) = sin 73°
cos (17°) = sin 73°
cos² 17° = sin² 73°

(ii) sin 25° cos 65° + cos 25° sin 65°
sin (90° – θ) = cos θ
sin (90° – 25°) = cos 25°
sin (90° – 65°) = cos 65°
sin 25° = cos 65°

cos (90° – θ) = sin θ
cos (90° – 65°) = sin 65°
cos 25° = sin 65°

sin 25° = cos 65°
cos 65° . cos 65° + sin 65° . sin 65°
∴ cos² 65 + sin² 65 = 1

Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec² A – 9 tan² A=
(A) 1
(B) 9
(C) 8
(D) 0
Solution :
9 sec² A – 9 tan² A
9(1 + tan² A) – 9 tan² A
9 + 9 tan² A – 9 tan² A = 9.
∴ 9 sec² A – 9 tan² A = 9.

(ii) (1 + tan θ + sec θ) (1 + cot 0 – cosec θ) =
(A) 0
(B) 1
(C) 2
(D) – 1
Solution :

(iii) (sec A + tan A) (1 – sin A) =
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
Solution :

(iv) \(\frac{1+\tan ^2 A}{1+\cot ^2 A}\) =
(A) sec² A
(B) – 1
(C) cot² A
(D) tan² A
Solution :

Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
Solution :

(viii) (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A.

LHS = sin² A + cosec² A + 2 sin A cosec A + cos² A + sec² A + 2 cos A sec A [∵ (a + b)² = a² + b² + 2ab]
= (sin² A + cos² A) + (1 + cot² A) + 2 sin A . \(\frac{1}{sin A}\) + (1 + tan² A) + 2 cos A . \(\frac{1}{cos A}\) (∵ 1 + cot² A = cosec² A and sec² A = 1 + tan² A)
= 1 + 1 + cot² A + 2 + 1 + tan² A + 2 (∵ sin² A + cos² A = 1)
= 7 + tan² A + cot² A = RHS.

(ix) (cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\)
Solution :
[Hint: Simplify LHS and RHS separately].
LHS = (cosec A – sin A) (sec A – cos A)

Jharkhand Board JAC Class 10 Maths Solutions Chapter 11 Constructions Ex 11.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 11 Constructions Exercise 11.1

In each of the following, give the justification of the construction also:

Question 1.
Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Solution :

Steps of construction:
1. Draw the line segment AB = 7.6 cm.
2. At A, below AB, make an angle BAx = 30°.
3. At B, above AB, make an angle ABy = 30°.
B\(\hat{A}\)x = A\(\hat{B}\)y = 30°
These are alternate angles. ∴ Ax || By.
4. With a convenient radius cut off five equal parts
AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ in Ax.
5. With the same radius cut off eight equal parts.
BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇ = B₇B₈.
6. Join A₅B₈. Let it cut AB at C.
AC : CB = 5 : 8.

In ΔACA₅ and CBB₈
1. A\(\hat{C}\)A₅ = B\(\hat{C}\)B₈ (V.O.A.)
2. C\(\hat{A}\)A₅ = A\(\hat{B}\)B₈ (Alternate angles)
3. C\(\hat{A}\)₅A = B\(\hat{B}\)₈C (Alternate angles)
Δs are equiangular.
∴\(\frac{\mathrm{AA}_5}{\mathrm{BB}_8}=\frac{\mathrm{CA}_5}{\mathrm{AB}_8}=\frac{\mathrm{CA}}{\mathrm{BC}}\)
∴ \(\frac{\mathrm{CA}}{\mathrm{BC}}=\frac{\mathrm{AA}_5}{\mathrm{BB}_8}=\frac{5}{8}\)

Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac{2}{3}\) of the corresponding sides of the first triangle.
Solution :

Steps of construction:

1. Construct ΔABC given AB = 4 cm, BC = 5 cm, AC = cm.
2. At B, make an acute angle CBx.
3. Divide Bx into three equal parts with a convenient radius.
4. Join B₃C.
5. From B₂ draw a parallel to B₃C.
6. Let it cut BC at C’.
7. At C’ make angle A’C’B = ACB.

Join A’C’.
∴ ΔABC ||| A’BC’.

In ΔABC and ΔA’BC’,
1.A\(\hat{B}\)C = A’\(\hat{B}\)C’ (Common angle)
2. A\(\hat{C}\)B = A’\(\hat{C’}\)B (Corresponding angles)
3. B\(\hat{A}\)C = B\(\hat{A’}\)C’ (Remaining angles)
Δs are equiangular.
∴ \(\frac{\mathrm{AC}}{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}=\frac{\mathrm{AB}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}=\frac{\mathrm{BC}}{\mathrm{BC} \mathrm{C}^{\prime}}\) = \(\frac{3}{2}\) ∴ [latex]\frac{BC’}{BC}=\frac{2}{3}[/latex]

Question 3.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are \(\frac{7}{5}\) of the corresponding sides of the first triangle.
Solution :
Steps of construction:

1. Construct a triangle ABC given BC= 7 cm, AB = 5 cm, AC = 6 cm.
2. At B, below BC, make an acute angle CBx.
3. With a convenient radius cut off seven equal parts BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇.
4. Join B₅C.
5. From B₁ draw a parallel to B₅C to cut BC produced at C’.
6. At C’ draw a parallel to CA to meet BA produced at A’.

A’BC’ is the required triangle.
In ΔABC and ΔA’BC’

Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1\(\frac{1}{2}\) times the corresponding sides of the isosceles triangle.
Solution :

Steps of construction:

1. Draw a line segment BC = 8 cm.
2. Draw its perpendicular bisector.
3. Cut off DA = 4 cm. (altitude given)
4. Join AB and AC. ABC is the required triangle.
5. At B, below BC, draw an acute angle CBx.
6. With a convenient radius cut off three equal parts BB₁ = B₁B₂ = B₂B₃.
7. Join B₂C.
8. At B₃ draw a parallel to B₂C to meet BC extended at C’.
9. At C’ draw a parallel to CA to meet BA produced at A’.
10. Join A’C’. A’BC’ is the required triangle similar to ΔABC.

In ΔA’BC’ and ABC
1. A’\(\hat{B}\)C’ = A\(\hat{B}\)C (Common angle)
2. B\(\hat{A}\)‘C’ = B\(\hat{A}\)C (Corresponding angles)
3. A’\(\hat{C}\)‘B = A\(\hat{C}\)B
Δs are equiangular.
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{\mathrm{BC}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}\)
\(\frac{BC’}{BC}\) = \(\frac{3}{2}\)
BC = 8 cm, BC’ = 8 × \(\frac{3}{2}\) = 12 cm.
BA = CA = 5.6 cm ∴ A’B = A’C’ = 5.6 × \(\frac{3}{2}\) = 8.4 cm.

Question 5.
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are \(\frac{3}{4}\) of the corresponding sides of the triangle ABC.
Solution :

Steps of construction:

1. Construct ΔABC given BC = 6 cm, AB = 5 cm, A\(\hat{B}\)C = 60°.
2. At B, below BC, make an acute angle CBx.
3. In Bx cut off four equal parts BB₁ = B₁B₂ = B₂B₃ = B₃B₄
4. Join B₄C.
5. From B₃ draw a parallel to B₄C to meet BC at C’.
6. At C’ draw a parallel to CA to meet CA at A’.

A’BC’ is the required triangle similar to ΔABC.
In Δs A’BC’ and ABC

Question 6.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are \(\frac{4}{3}\) times the corresponding sides of ΔABC.
Solution :

\(\hat{A}\) + \(\hat{B}\) + \(\hat{C}\) = 180°
\(\hat{A}\) + \(\hat{B}\) = 150° (105° + 45°)
∴ \(\hat{C}\) = 30°
Steps of construction:
1. In ΔABC, BC = 7 cm.
\(\hat{B}\) = 45°, \(\hat{C}\) = 105°
∴ \(\hat{A}\) = 180° – 45° – 105°
= 180° – 150° = 30°.
Construct ΔABC given BC = 7 cm, \(\hat{B}\) = 45°, \(\hat{C}\) = 30°.
2. At B draw an acute angle CBx.
3. In Bx cut off four equal parts BB₁ = B₁B₂ = B₂B₃ = B₃B₄ with a convenient radius.
4. Join B₃C.
5. At B₄ draw a parallel to B₃C to meet BC produced at C’.
6. At C’ make angle of 30° equal to A\(\hat{C}\)B. Let it meet BA produced at A’.
A’BC’ is the required triangle similar to ΔABC.
In ΔC’BB₄ CB₃ || C’B₄

Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are \(\frac{5}{3}\) times the corresponding sides of the given triangle.
Solution :

BC’ = \(\frac{5}{3}\) × BC = \(\frac{5}{3}\) × 3 = 5 cm
BA’= \(\frac{5}{3}\) × 4 = \(\frac{20}{3}\) = 6.6 cm
A’C’ = \(\frac{5}{3}\) × 5 = \(\frac{25}{3}\) = 8.3 cm.

Steps of construction:

1. Construct ΔABC given BC= 3 cm, \(\hat{B}\) = 90°, BA = 4 cm.
2. At B, make an acute angle CBx.
3. Cut off five equal parts BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ along Bx with a convenient radius.
4. Join B₃C.
5. At B₅ draw a parallel to B₃C to meet BC produced at C’.
6. At C’ draw a parallel to CA to meet BA produced at A’.

A’BC’ is the required triangle similar to ΔABC.
BC’ : BC = BB₅ = BB₃
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_5}{\mathrm{BB}_3}\) = \(\frac{5}{3}\)

In Δs A’BC’ and ABC
1. A’\(\hat{B}\)C’ = A\(\hat{B}\)C = 90°
2. B\(\hat{A}\)‘C’ = B\(\hat{A}\)C (Corresponding angles)
3. B\(\hat{C}\)‘A’ = B\(\hat{C}\)A
Δs are equiangular.
∴ \(\frac{A’C’}{AC}\) = \(\frac{BC’}{BC}\) = \(\frac{BA’}{BA}\) = \(\frac{5}{3}\)

Students should go through these JAC Class 10 Maths Notes Chapter 15 प्रायिकता will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 15 प्रायिकता

भूमिका :
कक्षा IX में हमने किसी घटना के प्रायोगिक या अनुभाविक प्रायिकता के बारे में अध्ययन किया था। स्मरण करें जिस प्रायिकता का अनुमापन हम वास्तविक प्रयोगों के परिणामों तथा घटनाओं के घटित होने की पर्याप्त रिकार्डिंग के आधार पर करते हैं, उस प्रायिकता को प्रायोगिक या आनुभाविक प्रायिकता कहते हैं।

प्रायिता-एक सैद्धान्तिक दृष्टिकोण :
उदाहरण के लिए-जब हम एक सिक्का उछालें तो यह समतल पर गिरेगा। यह एक क्रिया या प्रयोग है जिससे दो परिणाम प्राप्त हो सकते हैं-चित (अशोक वाला) तल दिखायी दे अथवा पट (दूसरा तल) दिखायी दे ये दो सम्भव घटनाएँ (Events) हैं।
(i) इस प्रकार हम देखते हैं कि सिक्का उछालने के किसी प्रयोग में कुल सम्भावित घटनाएँ दो हैं चित गिरने की सम्भावना 2 घटनाओं में से 1 है और पट गिरने की सम्भावना भी उतनी ही है। तब गणित की भाषा में हम कहते हैं कि सिक्के के चित गिरने की प्रायिकता \(\frac{1}{2}\) है। सिक्के के पट गिरने की भी प्रायिकता \(\frac{1}{2}\) है।

(ii) किसी चुनाव में A, B, C, D चार उम्मीदवार खड़े हैं, तब सफल प्रत्याशी के चुनाव की कुल 4 सम्भावनाएँ हैं, क्योंकि चारों प्रत्याशियों में से कोई भी सफल हो सकता है, तब प्रत्याशी A की सफलता की सम्भावना 4 में से 1 है।
हम गणित की भाषा में कह सकते हैं कि प्रत्याशी A की सफलता की प्रायिकता \(\frac{1}{4}\) है; शेष प्रत्याशियों B, C व D की सफलता की भी प्रायिकता उतनी ही है। यहाँ हम कह सकते हैं कि किसी प्रत्याशी की असफलता की प्रायिकता है क्योंकि एक प्रत्याशी के सफल होने की दशा में शेष 3 के असफल होने की घटना अवश्य घटित होगी।

(iii) ताश की गड्डी में से पत्ता खींचिए। इसके लाल होने की प्रायिकता पर विचार कीजिए। कुल 52 पत्तों की गड्डी में 26 लाल और 26 काले पत्ते होंगे, तब पत्ते के लाल होने की प्रायिकता \(\frac{26}{52}\) या \(\frac{1}{2}\) है। खींचे गए पत्ते के लाल न होने की भी प्रायिकता \(\frac{26}{52}\)या \(\frac{1}{2}\) ही है।
→ प्रायिकता (Probability) : जब किसी घटना के घटित होने की सम्भावना संख्यात्मक रूप में व्यक्त की जाती है तो उसे प्रायिकता कहते हैं।

→ प्रयोग (Experiment) : वह विधि जिसके द्वारा हमें किसी प्रेक्षण का परिणाम प्राप्त होता है प्रयोग कहलाता है।

→ परिणाम (Outcome) : किसी प्रयोग के विशिष्ट निष्कर्ष को परिणाम कहते हैं।

→ यादृच्छया प्रयोग (Random Experiment) : ऐसे प्रयोग जिनके निश्चित परिणाम नहीं हों यादृच्छया प्रयोग कहलाते हैं।

→ अभिप्रयोग (Trial) : किसी भी यादृच्छिक प्रयोग को करने की प्रक्रिया को एक अभिप्रयोग (trial) कहते है।

→ पूरक घटनाएँ (Complimentary events) : यदि ‘E’ किसी घटना के घटित होने की प्रायिकता है तथा ‘E नहीं’ न घटित होने की प्रायिकता है तब E और ‘E नहीं’ पूरक घटनाएँ कहलाती हैं।
∴ P(E) + P(E नहीं) = 1.

→ मिश्रित घटनाएँ (Compound events ) : किसी यादृच्छिक प्रयोग से जुड़ी ऐसी घटनाएँ जो दो या दो से अधिक प्रारम्भिक घटनाओं के मिश्रण से प्राप्त होती हैं, मिश्रित घटनाएँ कहलाती हैं।

→ अनुकूल प्रारंभिक घटना (Favourable elementary event) एक ऐसी प्रारम्भिक घटना जो किसी मिश्रित घटना के अनुकूल हो अनुकूल प्रारम्भिक घटना कहते हैं।

→ पासा (Dice or die) : एक छोटा घन जिसके पृष्ठों पर 1 से 6 तक संख्याएँ लिखी हों पासा कहलाता है। प्रायिकता एक सैद्धान्तिक दृष्टिकोण

→ यादृच्छया उछाल (Random toss) : किसी सिक्के को बिना किसी पक्षपात (bias) या रुकावट के स्वतन्त्रता पूर्वक गिरने दिया जाता है तो उसे यादृच्छया उछाल कहते हैं।

→ समप्रायिक (Equally likely) जब किसी यादृच्छया प्रयोग में किसी घटना E के सभी परिणामों के प्राप्त होने की सम्भावना समान होती है तो यह परिणाम समप्रायिक कहलाते हैं।
जैसे- किसी सिक्के को उछालने में चित या पट आना अथवा पाँसे की उछाल में पासे पर अंकित अंकों में से कोई अंक प्राप्त होने की घटना समप्रायिक घटनाएँ हैं।

→ सैद्धान्तिक प्रायिकता (Theoretical Probability) किसी प्रयोग में यदि एक घटना E घटित होती है और यह कल्पना करने पर प्रयोग में घटना E के सभी परिणाम बिल्कुल एक हों तो.

इस प्रकार से अवकलित प्रायिकता को सैद्धान्तिक प्रायिकता कहते हैं।

→ प्रारम्भिक घटना (Elementary event) : वह घटना है जिसका केवल एक ही परिणाम है। किसी पासे को उछालने पर 5 प्राप्त होना प्रारम्भिक घटना है क्योंकि 5 प्राप्त होने का केवल एक ही परिणाम है।
परन्तु विषम या सम संख्या प्राप्त होना प्रारम्भिक घटना नहीं है क्योंकि विषम संख्या प्राप्त होने की घटना के 1, 3, 5 तीन परिणाम हैं। ऐसे ही सम संख्या या 5 से छोटी संख्या प्राप्त होने की घटना भी प्रारम्भिक घटना नहीं है क्योंकि इनके परिणाम 1 से अधिक हैं।
किसी प्रयोग की सभी प्रारम्भिक घटनाओं की प्राथकिताओं का योग होता है।

→ असम्भव घटना (Impossible event) : ऐसी घटना जिसकी प्रायिकता शून्य होती है अर्थात् उस घटना का घटित होना असम्भव हो तो उस घटना को असम्भव घटना (Impossible Event) कहते हैं।
किसी पासे की उछाल में “6 से बड़ा अंक प्राप्त होने की घटना” असम्भव घटना है।

→ निश्चित घटना (Sure event) यदि किसी घटना की प्रायिकता हो तो उस घटना को निश्चित घटना (Sure event) कहते हैं।
जैसे-किसी पासे की फेंक में 7 से छोटी संख्या प्राप्त होने की घटना के सभी परिणाम 1, 2, 3, 4, 5, 6 सम्भव हैं। यह एक निश्चित घटना है।

→ घटना (E) घटित नहीं हो : इसे E1 या \(\bar{E}\) से व्यक्त करते हैं तथा घटना को “E नहीं” से जाना जाता है। यदि किसी घटना की प्रायिकता सदैव शून्य के बराबर या उससे अधिक तथा के बराबर या उससे कम होती है।
0 ≤ P(E) ≤ 1

ताश के पत्ते (Playing Cards) :
ताश की गड्डी में कुल पत्तों की संख्या = 52
कुल पत्ते 4 समूहों में विभाजित होते हैं-
(1) हुकुम (Spades), (2) पान (Hearts), (3) ईट (Diamonds), (4) चिड़ी (Clubs)

प्रत्येक समूह में तेरह पत्ते होते हैं अर्थात्
हुकुम के 13, पान के 13, ईंट के 13 और चिड़ी के 13 पत्ते होते हैं।
काले रंग के पत्ते : हुकुम 13 व चिड़ी 13 = कुल 26
लाल रंग के पत्ते : पान 13 व ईंट 13 = कुल 26
प्रत्येक समूह में इक्का (ace), बादशाह (king), बेगम (queen) और गुलाम (jack) उच्च क्रम के पत्ते होते हैं। इक्का (ace) पहले क्रम का पत्ता है और बादशाह (king), बेगम (queen) तथा गुलाम (jack) फेस पत्ते (face cards) कहलाते हैं।

ध्यान देने योग्य बिन्दु :

उक्त प्रकार से अवकलित प्रायिकता को सैद्धान्तिक प्रायिकता कहते हैं।
→ किसी प्रयोग की सभी प्रारम्भिक घटनाओं की प्रायिकता का योग 1 है। यह व्यापक रूप में भी सत्य है।
→ व्यापक रूप में किसी घटना E के लिए सत्य है कि P(\(\bar{E}\)) = 1 – P(E)
→ एक निश्चित या निर्धारित घटना की प्रायिकता 1 होती है।
→ एक असम्भव घटना की प्रायिकता 0 होती है।
→ घटना E की प्रायिकता एक ऐसी संख्या है, कि (PE)
0 ≤ P(E) ≤ 1
→ किसी भी घटना E के लिए P(E) + P(\(\bar{E}\)) = 1 होता है।
जहाँ \(\bar{E}\) घटना ‘E नहीं’ को व्यक्त करता है। E और \(\bar{E}\) पूरक घटनाएँ कहलाती हैं।
→ एक असम्भव घटना की प्रायिकता 0 (या 0%) होती है। जैसे-सूर्य के कभी अस्त नहीं होने की प्रायिकता 0 है।

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 15 प्रायिकता Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 15 प्रायिकता

लघुत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
किसी प्रयोग की सभी प्रारम्भिक घटनाओं की प्रायिकताओं का योग लिखिए।
हल:
किसी प्रयोग की सभी प्रारम्भिक घटनाओं की प्रायिकताओं का योग 1 होता है।

प्रश्न 2.
एक थैले में 3 लाल और 5 काली गेंदें हैं। इस थैले में से एक गेंद यादृच्छया निकाली जाती है। इसकी प्रायिकता क्या है कि गेंद काली नहीं है ?
हल:
थैले में गेंदों की कुल संख्या = 3 लाल + 5 काली = 8
∴ कुल सम्भव परिणाम = 8
काली गेंद न होने की घटना के अनुकूल परिणामों की संख्या = 3
∴ गेंद काली न होने की प्रायिकता = \(\frac{3}{8}\)

प्रश्न 3.
दो पासों को एक साथ फेंका जाता है। इसकी प्रायिकता क्या है कि दोनों पासों पर आने वाली संख्याओं का योग 7 है।
हल:
जब दो पासों को एक साथ फेंका जाता है तब सम्भावित परिणामों की संख्या = 6 × 6 = 36
दोनों पासों पर आने वाली ऐसी संख्याएँ जिनका योग 7 है :
(1, 6), (2, 5), (3, 4), (4, 3), (5, 2) और (6, 1)
∴ अनुकूल परिणामों की संख्या = 6
दोनों पासों पर आने वाली संख्याओं का योग 7 की प्रायिकता = \(\frac{6}{36}=\frac{1}{6}\)

प्रश्न 4.
52 पत्तों की अच्छी प्रकार से फेंटी गई ताश की एक गड्डी में से यादृच्छया एक पत्ता निकाला गया। प्रायिकता ज्ञात कीजिए कि निकाला गया पत्ता-
(i) लाल रंग का बादशाह है।
(ii) एक बेगम अथवा गुलाम है।
हल:
ताश की गड्डी में 52 पत्ते होते हैं तथा एक पत्ता 52 तरीकों से निकाला जा सकता है।
∴ कुल सम्भावित परिणामों की संख्या = 52
(i) माना कि लाल रंग का बादशाह होने की घटनां R है।
अतः घटना (R) के अनुकूल परिणामों की संख्या = 2
P(R) = \(\frac{2}{52}=\frac{1}{26}\)

(ii) माना कि एक गुलाम अथवा बेगम होने की घटना A है।
∴ घटना (A) के अनुकूल परिणामों की संख्या = 8
∴ P(A) = \(\frac{8}{52}=\frac{2}{13}\)
अत: (I) P(R) = \(\frac{1}{26}\), (ii) P(A) = \(\frac{2}{13}\)

प्रश्न 5.
52 पत्तों की ताश की एक गड्डी में से सभी बादशाह, बेगम तथा इक्के निकाल दिए गए। शेष बचे पत्तों को भली प्रकार फेंटने के पश्चात् उनमें से एक पत्ता निकाला गया। प्रायिकता ज्ञात कीजिए कि निकाला पत्ता-
(i) एक काले रंग का तस्वीर वाला पत्ता है।
(ii) एक लाल रंग का पत्ता है।
हल:
ताश की गड्डी में कुल पत्तों की संख्या = 52
बादशाह, बेगम तथा इक्के के पत्तों की संख्या = 12
बादशाह, बेगम तथा इक्के के पत्तों को निकालने के बाद शेष बचे पत्तों की संख्या 52 – 12 = 40
∴ कुल सम्भव परिणामों की संख्या = 40
(i) माना कि निकाले गए पत्ते की काले रंग के तस्वीर वाले पत्ते होने की घटना ‘A’ है।
40 पत्तों में काले रंग के तस्वीर वाले पत्तों की संख्या = 2
∴ घटना (A) के अनुकूल परिणामों की संख्या = 2
⇒ P(A) = \(\frac{2}{40}=\frac{1}{20}\)

(ii) माना कि निकाले गए पत्ते की लाल रंग का होने की घटना ‘B’ है।
लाल रंग के पत्तों की संख्या = 20
∴ घटना (B) के अनुकूल परिणामों की संख्या = 20
⇒ P(B) = \(\frac{20}{40}=\frac{1}{2}\)
अत: (i) P(A) = \(\frac{1}{20}\)
(ii) P(B) = \(\frac{1}{2}\)

प्रश्न 6.
एक पेटी में 30 डिस्क हैं, जिन पर 1 से 30 तक संख्याएँ अंकित हैं। यदि इस पेटी में से एक डिस्क यादृच्छया निकाली जाती है तो इसकी प्रायिकता ज्ञात कीजिए कि इस डिस्क पर अंकित होगी-
(i) दो अंकों की एक संख्या
(ii) एक पूर्ण वर्ग संख्या
हल:
दिया है : पेटी में कुल डिस्क = 30
(i) 30 डिस्क में से दो अंकों की संख्याएँ हो सकती हैं-
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30
दो अंकों की डिस्क के अनुकूल परिणाम = 21 डिस्क संभावित परिणाम = 30
अतः यादृच्छया दो अंकों की एक संख्या होने की प्रायिकता

(ii) एक पूर्ण वर्ग संख्या = 4, 9, 16, 25
अनुकूल परिणाम = 4
संभावित परिणाम = 30
अतः यादृच्छया एक पूर्ण वर्ग संख्या होने की प्रायिकता = \(\frac{4}{30}=\frac{2}{15}\)

प्रश्न 7.
अच्छी तरह से फेंटी गई एक ताश की गड्डी से एक पत्ता यादृच्छया निकाला गया। प्रायिकता ज्ञात कीजिए कि निकाला गया पत्ता-
(i) हुकुम का पत्ता है या एक इक्का है
(ii) एक काले रंग का बादशाह है
(iii) न तो गुलाम है तथा न ही बादशाह है
(iv) या तो बादशाह हैं या बेगम है
हल:
कुल पत्तों की संख्या = 52
(i) हुकुम और इक्का के पत्तों की संख्या 13 + 3 = 16
हुकुम और इक्का के निकलने की प्रायिकता = \(\frac{16}{52}=\frac{4}{13}\)
(ii) गड्डी में काले रंग का बादशाह = 2
काले रंग के बादशाह की प्रायिकता = \(\frac{2}{52}=\frac{1}{26}\)
(iii) गुलाम और बादशाह के पत्तों की संख्या = 4 + 4 = 8
एक गड्डी में न तो गुलाम है तथा न ही बादशाह के पत्तों की संख्या = 52 – 8 = 44
न गुलाम न बादशाह होने की प्रायिकता = \(\frac{44}{52}=\frac{11}{13}\)
(iv) एक गड्डी में बादशाह और बेगम के पत्तों की संख्या = 4 + 4 = 8
या तो बादशाह या बेगम होने की प्रायिकता = \(\frac{8}{52}=\frac{2}{13}\)

प्रश्न 8.
दो भिन्न पासों को एक साथ उछाला गया दोनों पासों के ऊपरी तलों पर आई संख्याओं का गुणनफल 6 आने की प्रायिकता ज्ञात कीजिए।
हल:
जब दोनों पासों को एक साथ फेंका जाता है तो संभावित परिणामों की संख्या 6 × 6 = 36
दोनों पासों पर संख्याओं का गुणनफल 6 प्राप्त होने की अनुकूल स्थितियाँ = (1, 6), (6, 1), (2, 3), (3, 2)
दोनों पासों का गुणनफल 6 होने के अनुकूल परिणामों की संख्या = 4
अभीष्ट परिणाम = \(\frac{4}{36}=\frac{1}{9}\)

प्रश्न 9.
एक जार में केवल लाल, नीली तथा नारंगी रंग की गेंदें हैं। यादृच्छया एक लाल रंग की गेंद के निकालने की प्रायिकता \(\frac{1}{4}\) है। इसी प्रकार उसी जार से यादृच्छया एक नीली गेंद निकालने की प्रायिकता \(\frac{1}{3}\) है। यदि नारंगी की कुल गेंदें 10 हैं, तो बताइए कि जार में कुल कितनी गेंदें हैं।
हल:
माना लाल, नीली तथा नारंगी गेंद निकालने की प्रायिकता क्रमश: E₁, E₂, E₃ है।
हम जानते हैं,
P(E₁) = \(\frac{1}{4}\)
P(E₂) = \(\frac{1}{3}\)
P(E₃) = 1 – PE₂ – PE₁
P(E₃) = \(1-\frac{1}{3}-\frac{1}{4}\)
P(E₃) = \(\frac{5}{12}\)
हमयह भी जानते हैं कि

कुल गेदों की संख्या = \(\frac{120}{5}\) = 24
अतः जार में गेंदों की कुल संख्या = 24 है।

प्रश्न 10.
एक जार में केवल नीले, काले तथा हरे कंचे हैं। इस जार में से यादृच्छया एक नीले कंचे के निकालने की प्रायिकता \(\frac{1}{5}\) है तथा उसी जार में से एक काले कंधे के यादृच्छयता निकालने की प्रायिकता \(\frac{1}{4}\) है। यदि जार में 11 हरे रंग के कंचे हैं, तो जार में कुल कंचों की संख्या ज्ञात कीजिए।
हल:
दिया है,
जार से नीले कंचे निकालने की प्रायिकता P(x) = \(\frac{1}{5}\)
जार से काले कंचे निकालने की प्रायिकता P(y) = \(\frac{1}{4}\)
जार में हरे कंचों की कुल संख्या = 11
माना, जार से हरे कंचे निकालने की प्रायिकता P(z) है।
अतः P(x) + P(y) + P(z) = 1

प्रश्न 11.
एक पिग्गी बैंक में, ₹ 1 के सौ सिक्के, ₹ 2 के 25 सिक्के, फू 5 के 15 सिक्के और ₹ 10 के दस सिक्के हैं। यदि पिग्गी बैंक को हिलाकर उल्टा करने पर कोई एक सिक्का गिरने के परिणाम समप्रायिक हैं, तो इसकी क्या प्रायिकता है कि वह गिरा हुआ सिक्का :
(i) ₹ 2 का होगा ?
(ii) ₹ 5 का होगा ?
हल:
कुल सम्भव परिणामों की संख्या = 100 + 25 + 15 + 10 = 150
(i) अनुकूल परिणामों की संख्या = 25
∴ ₹ 2 का सिक्का गिरने की प्रायिकता = \(\frac{25}{150}=\frac{1}{6}\)
(ii) अनुकूल परिणामों की संख्या = 15
∴ ₹ 5 का सिक्का गिरने की प्रायिकता = \(\frac{15}{150}=\frac{1}{10}\)

प्रश्न 12.
एक डिब्बे में 7 लाल कंचे, 10 सफेद कंचे और 5 हरे कंचे हैं। इस डिब्बे में से एक कंचा यादृच्छया निकाला जाता है। इसकी प्रायिकता क्या है कि निकाला गया कंचा (i) लाल नहीं है? (ii) सफेद है ? (iii) हरा है?
हल:
कुल सम्भव परिणामों की संख्या = 7 + 10 + 5 = 22
(i) अनुकूल परिणामों की संख्या = 7
लाल कंचे के निकलने की प्रायिकता = \(\frac{7}{22}\)
∴ लाल कंचे के न निकलने की प्रायिकता = \(1-\frac{7}{22}\)
= \(\frac{22-7}{22}=\frac{15}{22}\)
(ii) अनुकूल परिणामों की संख्या = 10
सफेद कंचे के निकलने की प्रायिकता = \(\frac{10}{22}=\frac{5}{11}\)
(iii) अनुकूल परिणामों की संख्या = 5
हरे कंचे के निकलने की प्रायिकता = \(\frac{5}{22}\)

प्रश्न 13.
दो विभिन्न पासों को एक साथ उछाला गया। निम्न के आने की प्रायिकता ज्ञात कीजिए :
(i) एक द्विक आना।
(ii) दोनों पासों पर आई संख्याओं का योग 10 आना।
हल:
दो पासों को एक साथ उछालने पर आने वाले कुल परिणाम = 36
(i) एक द्विक आने के संभावित परिणाम = [(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)]
कुल सम्भावित परिणामों की संख्या = 6
P (एक द्विक आना) = संभावित परिणाम / कुल परिणाम
= \(\frac{6}{36}=\frac{1}{6}\)
(ii) संख्याओं का योग 10 आने के संभावित परिणाम = [(4, 6), (5, 5) (6, 4)]
कुल संभावित परिणामों की संख्या = 5
P (योग 10) = संभावित परिणाम / कुल परिणाम
= \(\frac{6}{36}=\frac{1}{12}\)

प्रश्न 14.
1 से 100 के बीच की संख्याओं में से यादृच्छया एक संख्या चुनी गई। प्रायिकता ज्ञात कीजिए कि यह संख्या
(i) 8 से भाज्य है।
(ii) 8 से भाज्य नहीं है।
हल:
1 और 100 के बीच आने वाली कुल संख्या = 98
(i) 8 से भाज्य संख्या
= {(8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96}
कुल संभावित परिणामों की संख्या = 12
P(8 से भाज्य संख्या) = संभावित परिणाम / कुल परिणाम
= \(\frac{12}{98}=\frac{6}{49}\)

(ii) P(8 से अभाज्य संख्या)
\(P \bar{E}\) = 1 – P(E)
= 1 – \(\frac{6}{49}\) = \(\frac{43}{49}\)

प्रश्न 15.
एक थेले में 5 लाल गेंदे तथा कुछ नीली गेंदे हैं। यदि थैले में से यादृच्छया एक नीली गेंद निकालने की प्रायिकता, एक लाल गेंद के निकलने की प्रायिकता की तीन गुना है, तो थैले में नीली गेंदों की संख्या ज्ञात ‘कीजिए।
हल:
थैले में लाल गेंदों की संख्या = 5
माना थैले में नीली गेंदों की संख्या x है।
∴ थैले में से एक लाल गेंद निकालने की प्रायिकता = \(\frac{5}{x+5}\)
तथा थैले में से एक नीली गेंद निकालने की प्रायिकता = \(\frac{x}{x+5}\)
प्रश्नानुसार, \(\frac{x}{x+5}=3 \times \frac{5}{x+5}\)
⇒ \(\frac{x}{x+5}=\frac{15}{x+5}\)
⇒ x = 15
अतः थैले में नीली गेंदों की संख्या = 15

प्रश्न 16.
किसी यादृच्छया लिए गए वर्ष के नवम्बर मास में 5 रविवार होने की प्रायिकता ज्ञात कीजिए।
हल:
यादृच्छया लिए गए वर्ष के नवम्बर मास में 4 पूर्ण सप्ताह तथा 2 अन्य दिन होते हैं।
ये दो अन्य दिन निम्न में से कोई भी हो सकते हैं:
(सोम, मंगल), (मंगल, बुध), (बुध, गुरु), (गुरु, शुक्र), (शुक्ल, शनि), (शनि, रवि), (रवि, सोम)
पाँच रविवार होने के लिए अनुकूल परिणाम (शनि, रवि) तथा (रवि सोम)
अत: वांछित प्रायिकता = \(\frac{2}{7}\) ₹

प्रश्न 17.
तीन बच्चों वाले एक परिवारों में, कम-से-कम दो लड़के होने की प्रायिकता ज्ञात कीजिए।
हल:
तीन बच्चों वाले परिवारों में बच्चों के होने के परिणाम निम्नलिखित हैं :
{BBB, BBG, BGB, GBB, GGB, GBG, BGG, GGG}
कुल सम्भव परिणामों की संख्या = 8
कम-से-कम दो लड़के होने के अनुकूल परिणाम = {BBB, BBG BGB, GBB}
अनुकूल परिणामों की संख्या = 4
∴ कम से कम दो लड़के होने की प्रायिकता = \(\frac{4}{8}=\frac{1}{2}\)

वस्तुनिष्ठ प्रश्न :

(क) रिक्त स्थानों की पूर्ति कीजिए :
1. यदि P(E’) ‘नहीं की’ प्रायिकता 0.95 है, तो P(E) की प्रायिकता …………… होगी।
2. एक सिक्के को एक बार उछाला जाता है। इसे पट नहीं आने की प्रायिकता …………… है।
3. एक निश्चित घटने वाली घटना की प्रायिकता ……………. होती है।
4. अंग्रेजी वर्णमाला में से एक अक्षर यदृच्छया चुने जाने पर उसके व्यंजक होने की प्रायिकता ……………… है।
5. यदि किसी के जीतने की प्रायिकता 0.07 है तो उसके हारने की प्रायिकता …………….. है।
उत्तर:
1. 0.05,
2. \(\frac{1}{2}\)
3. 1
4. \(\frac{21}{26}\)
5. 0.93

(ख) निम्न में सत्य / असत्य बताइए :
1. एक पासा एक बार उछाले जाने पर 3 से छोटी संख्या प्राप्त करने की प्रायिकता \(\frac{1}{3}\) है।
2. 52 पत्तों की एक गड्डी में से एक लाल रंग के बादशाह आने की प्रायिकता \(\frac{1}{26}\) है।
3. यदि कल वर्षा होने की प्रायिकता 0.85 है, तो वर्षा न होने की प्रायिकता 0.58 है।
4. दो पासों को एक साथ फेंकने पर दोनों पासों पर संख्याओं का योग 13 आने की प्रायिकता \(\frac{2}{13}\) है।
5. यदि पासों के एक युग्म को एक बार उछाला गया, तो योगफल 8 आने की प्रायिकता \(\frac{5}{36}\) है।
उत्तर:
1. सत्य,
2. सत्य,
3. असत्य,
4. असत्य,
5. सत्य

बहुविकल्पीय प्रश्न :

प्रश्न 1.
एक थैले में 3 लाल, 5 काली तथा 7 सफेद गेंदे हैं। इस थैले में से एक गेंद को यादृच्छया निकाला जाता है। निकाली गई गेंद काली नहीं है, इसकी प्रायिकता है :
(A) \(\frac{1}{3}\)
(B) \(\frac{9}{15}\)
(C) \(\frac{5}{10}\)
(D) \(\frac{2}{3}\)
हल:
कुल गेंदे, n(S) = 3 + 5 + 7 = 15
अनुकूल परिणामों की संख्या = 5
∴ एक काली गेंद निकलने की प्रायिकता

अत: सही विकल्प (D) है।

प्रश्न 2.
संख्याओं 1, 2, 3, ……. 15 से यादृच्छया 4 का एक गुणज चुने जाने की प्रायिकता है:
(A) \(\frac{4}{15}\)
(B) \(\frac{2}{15}\)
(C) \(\frac{1}{15}\)
(D) \(\frac{1}{5}\)
हल:
कुल परिणाम की संख्या = 5
अनुकूल परिणाम = {4, 8, 12}
अनुकूल परिणामों की संख्या = 3
∴ 4 का गुणज चुने जाने की प्रायिकता = \(\frac{3}{15}=\frac{1}{5}\)
सही विकल्प (D) है।

प्रश्न 3.
दो सिक्के एक साथ उछाले गए। अधिक से अधिक एक चित आने की प्रायिकता है:
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{3}{4}\)
हल:
सम्भव परिणाम = {HT, HH, TH, TT}
कुल सम्भव परिणामों की संख्या = 4
अनुकूल परिणाम = {HT, TH}
अनुकूल परिणामों की संख्या = 2
अधिक से अधिक एक चित आने की प्रायिकता = \(\frac{2}{4}=\frac{1}{2}\)
सही विकल्प (B) है।

प्रश्न 4.
अच्छी प्रकार से फेंटी गई 52 पत्तों की ताश की गड्डी में से एक पत्ता यदृच्छया निकाला गया है। एक गुलाम के आने की प्रायिकता क्या है?
(A) \(\frac{3}{26}\)
(B) \(\frac{1}{52}\)
(C) \(\frac{1}{13}\)
(D) \(\frac{3}{52}\)
हल:
कुल सम्भव परिणामों की संख्या = 52
अनूकूल परिणामों की संख्या = 4
∴ गुलाम के आने की प्रायिकता = \(\frac{4}{52}=\frac{1}{13}\)
सही विकल्प (C) है।

प्रश्न 5.
किसी असम्भव घटना के होने की प्रायिकता है:
(A) 1
(B) \(\frac{3}{4}\)
(C) परिभाषित नहीं
(D) 0
हल:
सही विकल्प (D) हैं।

प्रश्न 6.
52 ताशों की एक गड्डी में से एक ताश निकाला जाता है। इसके लाल रंग का मुख कार्ड होने की प्रायिकता है :
(A) \(\frac{3}{26}\)
(B) \(\frac{1}{52}\)
(C) \(\frac{1}{13}\)
(D) \(\frac{3}{52}\)
हल:
ताश की गड्डी में कार्डों की कुल संख्या = 52
∴ कुल सम्भव परिणामों की संख्या = 52
लाल रंग के मुख कार्डों की संख्या = 6
∴ घटना के अनुकूल परिणामों की संख्या = 6
ताश की गड्डी में मुख कार्ड होने की प्रायिकता = \(\frac{6}{52}=\frac{3}{26}\)
अत: सही विकल्प (A) है।

प्रश्न 7.
52 ताशों की एक गड्डी में से एक कार्ड निकाला जाता है। कार्ड का ईंट का इक्का न होना घटना E है। E के अनुकूल परिणामों की संख्या है:
(A) 4
(B) 13
(C) 48
(D) 51
हल:
गड्डी में ताशों की कुल संख्या = 52
ताश की गड्डी में से एक कार्ड निकाला जाता है।
कार्ड का ईंट का इक्का न होना घटना E है।
∴ E के अनुकूल परिणामों की संख्या = 52 – 1 = 51
अत: सही विकल्प (D) है।

प्रश्न 8.
कोई लड़की यह परिकलित करती है कि उसके द्वारा एक लाटरी में प्रथम पुरुस्कार जीतने की प्रायिकता 0.08 है। यदि 6000 टिकट बेचे गए हैं तो उस लड़की ने कितने टिकट खरीदे हैं ?
(A) 40
(B) 240
(C) 480
(D) 750
हल:
बेचे गए टिकटों की संख्या = 6000
∴ कुल सम्भव परिणामों की संख्या = 6000
माना कि लड़की द्वारा खरीदे गए टिकटों की संख्या = x
∴ घटना के अनुकूल परिणामों की संख्या = x
प्रथम पुरुस्कार जीतने की प्रायिकता

⇒ x = 0.08 × 6000
⇒ x = 480
अत: सही विकल्प (C) है।

प्रश्न 9.
ताश की गड्डी में एक काले रंग के गुलाम न होने की प्रायिकता होगी :
(A) \(\frac{1}{26}\)
(B) \(\frac{3}{4}\)
(C) \(\frac{11}{52}\)
(D) \(\frac{25}{26}\)
हल:
ताश की गड्डी में कुल पत्तों की संख्या = 52
अतः कुल सम्भावित परिणामों की संख्या = 52
ताश की गड्डी में काले रंग के गुलाम (हुकम, चिढ़ी) होने के अनुकूल परिणामों की संख्या = 2
ताश की गड्डी में काले रंग के गुलाम होने की प्रायिकता = \(\frac{2}{52}=\frac{1}{26}\)
ताश की गड्डी में काले रंग के गुलाम न होने की प्रायिकता = \(1-\frac{1}{26}=\frac{25}{26}\)
अत: सही विकल्प (D) है।

प्रश्न 10.
एक थैले में कार्ड हैं जिन पर 2, 3, 4, …, 11 संख्याएँ अंकित हैं। थैले में से यादृच्छया एक कार्ड निकाला गया है। निकाले गए कार्ड पर एक अभाज्य संख्या होने की प्रायिकता है:
(A) \(\frac{1}{2}\)
(B) \(\frac{2}{5}\)
(C) \(\frac{3}{10}\)
(D) \(\frac{5}{9}\)
हल: थैले में कार्डों पर अंकित संख्याएँ हैं :
2, 3, 4, ………., 11
थैले में कार्डों की संख्या = 10
कार्डों पर अंकित अभाज्य संख्याएँ हैं :
2, 3, 5, 7, 11
कार्ड पर एक अभाज्य संख्या होने के अनुकूल परिणामों की संख्या = 5
∴ कार्ड पर एक अभाज्य संख्या होने की प्रायिकता = \(\frac{5}{10}=\frac{1}{2}\)
अतः सही विकल्प (A) है।

प्रश्न 11.
एक बक्से में कार्ड हैं जिन पर 6 से 50 तक की संख्याएँ अंकित हैं। बक्से में से यादृच्छया एक कार्ड निकाला गया। इस कार्ड पर अंकित संख्या के एक पूर्ण वर्ग होने की प्रायिकता है:
(A) \(\frac{1}{45}\)
(B) \(\frac{2}{15}\)
(C) \(\frac{1}{9}\)
(D) \(\frac{4}{45}\)
हल:
बक्से में कार्डों पर 6 से 50 तक की संख्याएँ अंकित हैं।
कुल सम्भव परिणामों की संख्या = 45
कार्डों पर अंकित पूर्ण वर्ग संख्याएँ हैं:
9, 16, 25, 36, 49
कार्ड पर पूर्ण वर्ग संख्या होने के अनुकूल परिणामों की संख्या = 5
कार्ड पर पूर्ण वर्ग संख्या होने की प्रायिकता = \(\frac{5}{45}=\frac{1}{9}\)
अतः सही विकल्प (C) है।

प्रश्न 12.
एक पासे को एक बार फेंका जाता है। एक विषम संख्या के आने की प्रायिकता है :
(A) 1
(B) \(\frac{1}{9}\)
(C) \(\frac{4}{6}\)
(D) \(\frac{2}{6}\)
हल:
एक पासे को एक बार फेंका जाता है तो पासे के पृष्ठों पर आने वाली संख्याएँ हैं :
{1, 2, 3, 4, 5, 6}
∴ सम्भव परिणामों की संख्या = 6
तथा अभाज्य संख्याएँ हैं : {1, 3, 5}
अभाज्य संख्या आने के अनुकूल परिणामों की संख्या = 3
अभाज्य संख्या आने की प्रायिकता = \(\frac{3}{6}=\frac{1}{2}\)
अतः सही विकल्प (B) है।

प्रश्न 13.
किसी स्कूल में पाँच सदन A, B, C, D और E हैं। किसी कक्षा में 23 विद्यार्थी हैं, जिनमें से 4 सदन A से, 8 सदन B से, 5 सदन C से 2 सदन D से तथा शेष सदन E से हैं। इनमें से एक विद्यार्थी को कक्षा का मॉनीटर बनाने के लिए चुना जाता है। चुने गए इस विद्यार्थी के सदनों A, B और C से न होने की प्रायिकता है :
(A) \(\frac{4}{23}\)
(B) \(\frac{6}{23}\)
(C) \(\frac{8}{23}\)
(D) \(\frac{17}{23}\)
हल:
कक्षा में विद्यार्थियों की कुल संख्या = 23
सदन A, B तथा C में विद्यार्थियों की संख्या का योग = 4 + 8 + 5 = 17
कुल सम्भव परिणामों की संख्या = 23
घटना के अनुकूल परिणामों की संख्या = 17
विद्यार्थी के सदनों A, B और C से होने की प्रायिकता = \(\frac{17}{23}\)
विद्यार्थी के सदनों A, B और C से न होने की प्रायिकता = \(1-\frac{17}{23}=\frac{6}{23}\)
अतः सही विकल्प (B) है।

प्रश्न 14.
यदि दो पासों को एक साथ फेंका जाता है तो दोनों पाँसों पर एक ही संख्या प्राप्त होने की प्रायिकता होगी :
(A) \(\frac{1}{6}\)
(B) \(\frac{5}{6}\)
(C) \(\frac{1}{36}\)
(D) इनमें से कोई नहीं
हल:
जब दोनों पासों को एक साथ फेंका जाता है तो सम्भावित परिणामों की संख्या = 6 × 6= 36
दोनों पाँसों पर एक जैसी संख्या प्राप्त होने की अनुकूल स्थितियाँ
(1, 1); (2, 2); (3, 3); (4, 4); (5, 5); (6, 6)
दोनों पासों पर एक जैसी संख्या प्राप्त होने के अनुकूल परिणामों की संख्या = 6
अभीष्ट प्रायिकता = \(\frac{6}{36}=\frac{1}{6}\)
अंत: सही विकल्प (A) है।

प्रश्न 15.
इसकी प्रायिकता कि यादृच्छिक रूप से चुने गए एक ऐसे वर्ष में, जो अधिवर्ष (leap year) न हो 53 रविवार हों, निम्नलिखित हैं :
(A) \(\frac{1}{7}\)
(B) \(\frac{2}{7}\)
(C) \(\frac{3}{7}\)
(D) \(\frac{5}{7}\)
हल:
एक साधारण वर्ष (Non leap year) में 365 दिन होते हैं।
365 दिन में 52 सप्ताह व 1 दिन होते हैं।
अर्थात् 365 दिन में 52 सप्ताह में 52 रविवार होंगे जो 1 दिन बचा है। वह निम्न में से एक हो सकता है।
रविवार, सोमवार, मंगलवार, बुधवार, गुरूवार, शुक्रवार, शनिवार
∴कुल सम्भव परिणामों की संख्या = 7
रविवार आने की घटना के अनुकूल परिणामों की संख्या = 1
रविवार होने की प्रायिकता = \(\frac{1}{7}\)
अत: सही विकल्प (A) है।

Jharkhand Board JAC Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Exercise 8.1

Question 1.
Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan² 45° + cos² 30° – sin² 60°

Solution :
(i) sin 60° cos 30° + sin 30° cos 60°
\(\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}\) + \(\frac{1}{2} \times \frac{1}{2}\)
\(\frac{3}{4}+\frac{1}{4}\) = 1

(ii) 2 tan² 45° + cos² 30° – sin² 60°
2(tan 45)² + (cos 30)² – (sin 60)²
2(1)² + (\(\frac{\sqrt{3}}{2}\))² – (\(\frac{\sqrt{3}}{2}\))² = 2

Question 2.
Choose the correct option and justify your choice:
(i) \(\frac{2 \tan 30^{\circ}}{1+\tan ^2 30^{\circ}}\)
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sin 30°
Solution :

(ii) \(\frac{1-\tan ^2 45^{\circ}}{1+\tan ^2 45^{\circ}}\) =
(A) tan 90°
(B) 1
(C) sin 45°
(D) 0
Solution :
\(\frac{1-(-1)^2}{1+(1)^2}=\frac{0}{2}\) = 0

(iii) sin 2A = 2 sin A is true when A =
(A) 0°
(B) 30°
(C) 45°
(D) 60°
Solution :
sin 2A = sin 0° = 0
2 sin A = 2 sin 0° = 2(0) = 0.

(iv) \(\frac{2 \tan 30^{\circ}}{1-\tan ^2 30^{\circ}}\) =
(A) cos 60°
(B) sin 60°
(C) tan 60°
(D) sin 30°
Solution :

Question 3.
If tan (A + B) = \(\sqrt{3}\) and tan (A – B) = \(\frac{1}{\sqrt{3}}\), 0° < A + B ≤ 90°; A > B, find A and B.
Solution :
tan(A + B) = \(\sqrt{3}\)
tan 60° = \(\sqrt{3}\)
∴ A + B = 60°
tan (A – B) = \(\frac{1}{\sqrt{3}}\)
tan 30° = \(\frac{1}{\sqrt{3}}\)
∴ A – B = 30°
∴ \(\hat{\mathbf{A}}\) = 45°, \(\hat{\mathbf{B}}\) = 15°

A + B = 60°
45 + B = 60°
B = 60 – 45 = 15
∴ B = 15°

Question 4.
State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Solution :
i) Let A = 30°, B = 60°.
sin 30° = \(\frac{1}{2}\)
sin 30 + sin 60°
sin (A + B) = sin 90° = 1
sin 60° = \(\frac{\sqrt{3}}{2}\)
\(\frac{1}{2}+\frac{\sqrt{3}}{2}\) = \(\frac{1+\sqrt{3}}{2}\)
sin (A+B) sin A + sin B
False.

iv) [θ = 0] sin 0 = 0
cos 0 = 1

θ = 30° sin 30° = \(\frac{1}{2}\)
cos 30° = \(\frac{\sqrt{3}}{2}\)

θ = 45° sin 45° = \(\frac{1}{\sqrt{2}}\)
cos 45° = \(\frac{1}{\sqrt{2}}\)

θ = 60° sin 60° = \(\frac{\sqrt{3}}{2}\)
cos 60° = \(\frac{1}{2}\)

θ = 90° sin 90° = 1
cos 90° = 0
False, because it is true only for θ = 45°.

(v) cot A = \(\frac{cos A}{sin A}\) . cot 0° = \(\frac{cos 0°}{sin 0°}\) = \(\frac{1}{0}\) = Undefined. True.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 5 Arithmetic Progressions Ex 5.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 5 Arithmetic Progressions Exercise 5.2

Question 1.
Fill in the blanks in the following table, given that a is the first term, d the common difference and a, the nth term of the AP:

Solution:
1. Here, a = 7, d = 3, n = 8 and a_n is to be found.
We have a_n = a + (n – 1)d
a₈ = 7 + (8 – 1) 3 = 7 + 21 = 28

2. Here, a = -18, n = 10, a_n = a₁₀ = 0 and d is to be found.
a_n = a + (n – 1)d
∴ 0 = – 18 + (10 – 1)d
∴ 18 = 9d ∴ d = 2

3. Here, d = -3, n = 18, a_n = a₁₈ = -5 and a is to be found.
an = a + (n – 1)d
∴ -5 = a + (18 – 1)(-3)
∴ -5 = a – 51
∴ a = 51 – 5 ∴ a = 46

4. Here, a = -18.9, d = 2.5, a_n = 3.6 and n is to be found.
a_n = a + (n – 1)d
∴ 3.6 = – 18.9 + (n – 1)(2.5)
∴ 22.5 = 2.5 (n – 1)
∴ (n – 1) = \(\frac{22.5}{2.5}\)
∴ n – 1 = 9 ∴ n = 10

5. Here, a = 3.5, d = 0, n = 105 and a_n is to be found.
a_n = a + (n – 1) d
∴ a₁₀₅ = 3.5 + (105 – 1) (0)
∴ a₁₀₅ = 3.5

Question 2.
Choose the correct choice in the following and justify:
1. 30th term of the AP: 10, 7, 4, ……, is
(A) 97
(B) 77
(C) -77
(D) -87
2. 11th term of the AP: -3, –\(\frac{1}{2}\), 2, ….. is
(A) 28
(B) 22
(C) -38
(D) -48\(\frac{1}{2}\)
Solution:
1. For the given AP 10, 7, 4,… a = 10,
d = 7 – 10 = -3 and n = 30
a_n = a + (n – 1)d
∴ a₃₀ = 10 + (30 – 1) (-3)
∴ a₃₀ = 10 – 87
∴ a₃₀ = -77
Thus, the correct choice is (C) -77.

2. For the given AP -3, –\(\frac{1}{2}\), 2, ….., a = -3.
d = –\(\frac{1}{2}\) – (-3) = 2\(\frac{1}{2}\) = \(\frac{5}{2}\) and n = 11.
a_n = a + (n – 1)d
∴ a₁₁ = -3 + (11 – 1)(\(\frac{5}{2}\))
∴ a₁₁ = – 3 + 25
∴ a₁₁ = 22
Thus, the correct choice is (B) 22.

Question 3.
In the following APs, find the missing terms in the boxes:

Solution:
For the given AP, first term = a = 2 and third term = a + 2d = 26.
a = 2 and a + 2d = 26 gives d = 12.
Then, second term = a + d = 2 + 12 = 14
Thus, the missing term in the box is

2. For the given AP,
second term = a + d = 13 …….(1)
fourth term = a + 3d = 3 …….(2)
Solving equations (1) and (2) we get d = -5 and a = 18.
Now, first term = a = 18 and third term = a + 2d
= 18 + 2(-5) = 8.
Thus, the missing terms in the boxes are

Alternative Method:
Let the terms of the given AP be a₁, a₂, a₃, a₄.
Here, a₂ = 13 and a₄ = 3.
Now, a₄ – a₃ = a₃ – a₂ = d
∴ 3 – a₃ = a₃ – 13
∴ 2a₃ = 16
∴ a₃ = 8
Again, a₂ – a₁ = a₃ – a₂
∴ 13 – a₁ = 8 – 13
∴ 13 – a₁ = -5
∴ a₁ = 18
Thus, the missing terms in the boxes are

3. For the given AP
first term a = 5 ……….(1)
fourth term = a + 3d = 9\(\frac{1}{2}\) ……….(2)
From equations (1) and (2), we get a = 5 and d = 1\(\frac{1}{2}\).
Now, second term = a + d = 5 + 1\(\frac{1}{2}\) = 6\(\frac{1}{2}\)
and third term = a + 2d = 5 + 2 (1\(\frac{1}{2}\)) = 8
Thus, the missing terms in the boxes are

4. For the given AP
first term a = -4 ……….(1)
sixth term = a + 5d = 6 ……….(2)
From equations (1) and (2), we get
a = -4 and d = 2
Now, second term = a + d(-4) + 2 = -2,
third term = a + 2d = (-4) + 2 (2) = 0.
fourth term = a + 3d = (-4) + 3(2) = 2 and
fifth term = a + 4d = (-4) + 4(2) = 4.
Thus, the missing terms in the boxes are

5. For the given AP,
second term = a + d = 38 ……….(1)
sixth term = a + 5d = -22 ……….(2)
Solving equations (1) and (2), we get
d = -15 and a = 53.
Now, first term = a = 53,
third term = a + 2d = 53 + 2(-15) = 23,
fourth term = a + 3d = 53 + 3(-15) = 8 and
fifth term = a + 4d = 53 + 4(-15) = -7.
Thus, the missing terms in the boxes are

Question 4.
Which term of the AP: 3, 8, 13, 18, … is 78 ?
Solution:
Suppose nth term of the AP 3, 8, 13, 18, … is 78.
Here, a = 3, d = 8 – 3 = 5, a_n = 78 and n is to be found.
a_n = a + (n – 1)d
∴ 78 = 3 + (n – 1)5
∴ 75 = 5 (n-1)
∴ 15 = n – 1 ∴ n = 16
Thus, the 16th term of the AP 3, 8, 13, 18, …….., is 78.

Question 5.
Find the number of terms in each of the following APs:
1. 7, 13, 19, …….., 205
2. 18, 15\(\frac{1}{2}\), 13, ……., -47
Solution:
1. For the given finite AP 7, 13, 19, ….. 205, a = 7, d = 13 – 76 and last term l = 205.
Let us consider that the last term is the nth term.
a_n = a + (n – 1)d
∴ 205 = 7 + (n – 1)6
∴ 198 = 6 (n – 1)
∴ n – 1 = 33
∴ n = 34
Thus, there are 34 terms in the given finite AP.

2. For the given finite AP 18, 15\(\frac{1}{2}\), 13….. -47, a = 18, d = 15\(\frac{1}{2}\) – 18 = -2\(\frac{1}{2}\) = –\(\frac{5}{2}\) and last term l = -47.
Let us consider that the last term is the nth term.
a_n = a + (n – 1) d
∴ -47 = 18 + (n-1) (-\(\frac{5}{2}\))
∴ -65 = –\(\frac{5}{2}\)(n – 1)
∴ n – 1 = 26
∴ n = 27
Thus, there are 27 terms in the given finite AP.

Question 6.
Check whether -150 is a term of the AP: 11, 8, 5, 2…
Solution:
If possible, let -150 be the nth term of the AP 11, 8, 5, 2,…
Here, a = 11; d = 8 – 11 = -3 and a_n = -150.
a_n = a + (n – 1)d
∴ -150 = 11 + (n – 1)(-3)
∴ -161 = -3 (n – 1)
∴ n – 1 = \(\frac{161}{3}\)
∴ n = \(\frac{164}{3}\)
∴ But n must be positive integer for an AP.
Hence, -150 cannot be a term of the AP 11, 8, 5, 2…..

Question 7.
Find the 31st term of an AP whose 11th term is 38 and the 16th term is 73.
Solution:
For any AP, a_n = a + (n – 1)d.
a₁₁ = a + 10 d
∴ a + 10 d = 38 ………(1)
∴ a₁₆ = a + 15d
∴ a + 15d = 73 ………(2)
Solving equations (1) and (2), we get
d = 7 and a = -32.
Now, 31st term = a₃₁ = a + 30d
= -32 + 30(7)
= -32 + 210
= 178
Thus, the 31st term of the given AP is 178.
Note: d = \(\frac{a_{16}-a_{11}}{16-11}=\frac{73-38}{5}=\frac{35}{5}=7\) can also be used.

Question 8.
An AP consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term.
Solution:
The given finite AP has 50 terms, hence its last term is a₅₀.
So, a₃ = 12 and a₅₀ = 106.
Now, a_n = a + (n – 1)d.
That gives, a₃ = a + 2d = 12 ………(1)
and a₅₀ = a + 49d = 106 ………(2)
Solving equations (1) and (2), we get
d = 2 and a = 8.
Now, 29th term = a₂₉ = a + 28d
∴ a₂₉ = 8 + 28 (2)
∴ a₂₉ = 64
Thus, the 29th term of the given AP is 64.

Question 9.
If the 3rd and the 9th terms of an AP are 4 and -8 respectively, which term of this AP is zero?
Solution:
For the given AP, a₃ = 4 and a9 = -8
We know, a_n = a + (n – 1)d.
∴ a₃ = a + 2d = 4 ………(1)
and a₉ = a + 8d = -8 ………(2)
Solving equations (1) and (2), we get
d = -2 and a = 8.
Now, let nth term of the AP be 0.
a_n = a + (n – 1)d
∴ 0 = 8 + (n – 1) (-2)
∴ 2(n – 1) = 8
∴ n – 1 = 4
∴ n = 5
Thus, the 5th term of the given AP is zero.

Question 10.
The 17th term of an AP exceeds its 10th term by 7. Find the common difference.
Solution:
For the given AP,
a₁₇ + 16d = a + 9d + 7a [∵ a_n = a + (n – 1) d]
∴ 7d = 7
∴ d = 1.
Thus, the common difference of the given AP is 1.

Question 11.
Which term of the AP:3, 15, 27, 39, …….. will be 132 more than its 54th term?
Solution:
For the given AP 3, 15, 27, 39, …….., a = 3
and d = 15 – 3 = 12.
Suppose nth term of the AP is 132 more than its 54th term.
∴ a_n = a₅₄ + 132
∴ a + (n – 1)d = a + 53d + 132
∴ 3 + (n – 1) (12) = 3 + 53(12) + 132
∴ 12(n – 1) = 12 (53 + 11)
∴ 12(n – 1) = 12 × 64
∴ n – 1 = 64
∴ n = 65
Thus, the 65th term of the given AP is 132 more than its 54th term.

Question 12.
Two APs have the same common difference. The difference between their 100th terms is 100, what is the difference between their 1000th terms?
Solution:
Let the first term of two given APs be a₁ and a₂ respectively and let the same common difference be d.
Also, let a₁ > a₂
Then, 100th term of the first AP = a₁ + 99d
(a_n = a + (n – 1)d)
100th term of the second AP = a₂ + 99d.
The difference between their 100th terms is 100.
∴ (a₁ + 99d) – (a₂ + 99d) = 100 (a₁ > a₂)
∴ a₁ – a₂ = 100 ……(1)
Now, 1000th term of the first AP = a₁ + 999d
1000th term of the second AP = a₂ + 999d.
Then, the difference between their 1000th terms
= (a₁ + 999d) – (a₂ + 999d)
= a₁ – a₂
= 100 (by (1))
Thus, the difference between the 1000th terms of the two APs is 100.

Question 13.
How many three digit numbers are divisible by 7?
Solution:
The list of three digit numbers divisible by 7 is as below:
105, 112, 119, …….., 987, 994.
These numbers form a finite AP with a = 105, d = 112 – 105 = 7 and last term l = 994.
Suppose the last term of the AP is its nth term.
∴ l = a_n
∴ 994 = a + (n – 1)d
∴ 994 = 105 + (n – 1)7
∴ 7(n – 1) = 889
∴ n – 1 = 127
∴ n = 128
Hence, there are 128 terms in the AP.
Hence, 128 three digit numbers are divisible by 7.

Question 14.
How many multiples of 4 lie between 10 and 250?
Solution:
The multiples of 4 lying between 10 and 250 give rise to following finite AP:
12, 16, 20, ….., 244, 248.
Here, a = 12, d = 16 – 12 = 4 and last term l = 248.
If the last term is the nth term of the AP then l = a_n.
∴ l = a + (n – 1) d
∴ 248 = 12 + (n – 1)4
∴ 236 = 4 (n – 1)
∴ n – 1 = 59
∴ n = 60
Thus, there are 60 terms in the AP.
Thus, 60 multiples of 4 lie between 10 and 250.

Question 15.
For what value of n, are the nth terms of two APs 63, 65, 67, …… and 3, 10, 17,… equal?
Solution:
For the first AP 63, 65, 67, ….., a = 63, d = 65 – 63 = 2.
Then, nth term of the first AP a is given by a_n = a + (n – 1)d = 63 + (n – 1)(2).
For the second AP 3, 10, 17, ……, A = 3, D = 10 – 3 = 7.
Then, nth term of the second AP An is given by
A_n = A + (n – 1) D = 3 + (n – 1) (7).
Now, a_n = A_n
∴ 63 + (n – 1) (2) = 3 + (n – 1)(7)
∴ 63 – 3 = (n – 1)(7 – 2)
∴ 60 = 5(n – 1)
∴ n – 1 = 12
∴ n = 13
Thus, for n = 13, the nth term of two given APs are equal.

Question 16.
Determine the AP whose third term is 16 and the 7th term exceeds the 5th term by 12.
Solution:
For the given AP a₃ = 16 and a₇ = a₅ + 12.
For any AP, a_n = a + (n – 1) d.
∴ a + 2d = 16 and a + 6d = a + 4d + 12
a + 6d = a + 4d + 12 gives 2d = 12,
i.e., d = 6.
Substituting d = 6 in a + 2d = 16, we get a = 4.
Then, the required AP is 4, 4 + 6, 4 + 2 (6), 4 + 3(6), …..
Hence, the required AP is 4, 10, 16, 22, ……

Question 17.
Find the 20th term from the last term of the AP: 3, 8, 13, ….., 253.
Solution:
For the given finite AP 3, 8, 13, …., 253,
a = 3, d = 8 – 3 = 5 and last term l = 253.
Let the last term be its nth term.
∴ l = a_n
∴ l = a + (n – 1)d
∴ 253 = 3 + (n – 1)(5)
∴ 250 = 5 (n – 1)
∴ n – 1 = 50
∴ n = 51
Thus, there are in all 51 terms in the AP.
Now, the 20th term from the last term is (51 – 20 + 1)th term = 32nd term from the beginning.
a₃₂ = a + 31d
∴ a₃₂ = 3 + 31(5)
∴ a₃₂ = 158
Thus, the 20th term from the last term is 158.

Question 18.
The sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and 10th terms is 44. Find the first three terms of the AP.
Solution:
For any AP, a_n = a + (n – 1) d.
a₄ = a + 3d, a₈ = a + 7d, a₆ = a + 5d and a₁₀ = a + 9d.
Now, a₄ + a₈ = 24 (Given)
∴ (a + 3d) + (a + 7d) = 24
∴ 2a + 10d = 24
∴ a + 5d = 12 ……..(1)
Again, a₆ + a₁₀ = 44 (Given)
∴ (a + 5d) + (a + 9d) = 44
∴ 2a + 14d = 44
∴ a + 7d = 22 …….(2)
Solving equations (1) and (2), we get d = 5 and a = -13.
Then, a₂ = a + d = 13 + (5) = -8 and
a₃ = a + 2d = -13 + 2(5) = -3.
Thus, the first three terms of the AP are -13, 8, 3.

Question 19.
Subba Rao started work in 1995 at an annual salary of ₹ 5,000 and received an increment of ₹ 200 each year. In which year did his income reach ₹ 7,000?
Solution:
Subba Rao’s income in first year = ₹ 5,000
His income in second year = ₹ 5,000 + ₹ 200
= ₹ 5200
His income in third year = ₹ 5200 + ₹ 200
= ₹ 5400
and so on.
These numbers of his income (in rupees) form the AP 5000, 5200, 5400, …….
Here, a = 5000; d = 5200 – 5000 = 200;
a_n = 7000 and n is to be found.
a_n = a + (n – 1)d
∴ 7000 = 5000 + (n – 1)(200)
∴ 2000 = 200(n – 1)
∴ n – 1 = 10
∴ n = 11
Thus, Subba Rao’s income will reach ₹ 7000 in 11th year, i.e., in the year 2005.

Question 20.
Ramkali saved ₹ 5 in the first week of a year and then increased her weekly savings by ₹ 1.75. If in the nth week, her weekly savings become ₹ 20.75, find n.
Solution:
Ramkali’s savings in first week = ₹ 5
her savings in second week = ₹ 5 + ₹ 1.75
= ₹ 6.75,
her savings in third week = ₹ 6.75 + ₹ 1.75
= ₹ 8.50.
and so on.
Thus, the weekly savings (in rupees) of Ramkalt form the AP 5, 6.75, 8.50, …..
Here, a = 5; d = 6.75 – 5 = 1.75; a_n = 20.75 and n is to be found.
a_n = a + (n – 1)d
∴ 20.75 = 5 + (n – 1)(1.75)
∴ 1.75(n – 1) = 15.75
∴ n – 1 = 9
∴ n = 10
Thus, if Ramkali’s weekly savings is ₹ 20.75 in nth week, then n = 10.