Class 9

JAC Board Class 9th Social Science Solutions Economics Chapter 3 Poverty as a Challenge

JAC Class 9th Economics Poverty as a Challenge InText Questions and Answers

Page No. 32

Question 1.
Why do different countries use different poverty lines?
Answer:
Different countries use different poverty lines because what is necessary to satisfy basic needs is different at different times and in different countries. Each country uses an imaginary line that is considered appropriate for its existing level of development and its accepted minimum social norms.

Question 2.
What do you think would be the “minimum necessary level” in your locality?
Answer:
The “minimum necessary level” in our locality would be ₹5000 per month per head.

Page No. 33

Table 3.1 Estimates of Poverty in India

Poverty Ratio (%)				Number of Poor (in million)
Year	Rural	Urban	Total	Rural	Urban	Combined
1993-94	50.7	32	45	329	75	404
2004-05	42	26	37	326	81	407
2009-10	34	21	30	278	76	355
2011-12	26	14	22	217	53	270

(Source Economic Survey 2017-18.)

Question 1.
Even if poverty ratio declined between 1993-94 and 2004-05, why did the number of poor remain at about 407 million?
Answer:
Though poverty ratio declined between 1993-94 and 2004-05, the number of poor remained at about 407 million due to population explosion during this period.

Question 2.
Are the dynamics of poverty reduction the same in rural and urban India?
Answer:
No, the dynamics of poverty reduction are not the same in rural and urban India.

Page. No. 35

Observe some of the poor families around you and try to find the following:
Question 1.
Which social and economic group do they belong to?
Answer:
They belong to scheduled castes and scheduled tribes and some are daily wages labourers.

Question 2.
Who are the earning members in the family?
Answer:
Both males and females are the earning members in the family.

Question 3.
What is the condition of the old people in the family?
Answer:
The condition of the old people in the family is very bad. They are treated as a burden on the family.

Question 4.
Are all the children (boys and girls) attending schools?
Answer:
No, all the children (boys and girls) are not attending schools. Only some boys are attending schools while girls are made to sit at home.

Page. No. 36

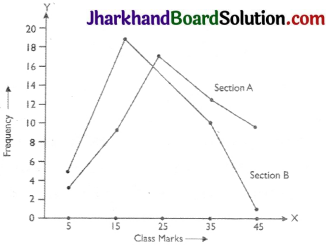
Graph 3.2 : Poverty Ratio in Selected Indian States (As per 2011 census)

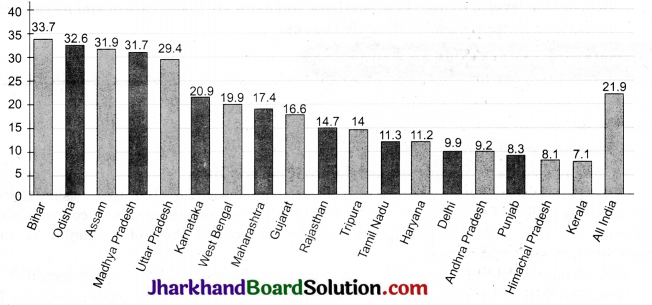
[Source Economic Survey 2017-18

Study the Graph 3.2 and do the following:
Question 1.
Identify the three states where the poverty ratio is the highest.
Answer:

1. Bihar.
2. Odisha.
3. Assam.

Question 2.
Identify the three states where poverty ratio is the lowest.
Answer:

1. Kerela.
2. Himachal Pradesh.
3. Punjab.

Page. No. 36

Graph 3.4 Number of the poor by region ($ 1.90 per day) in millions

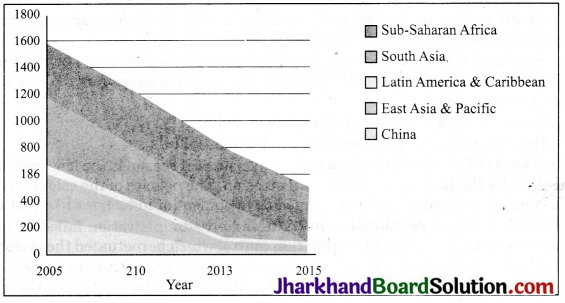
(Source Poverty and Equity Database: Word Bank (http://databank.worldbank.org/data/ reports. aspx?source=poverty-and-equity-database)

Study the Graph 3.4 and do the following:
Question 1.
Identify the areas of the world, where poverty ratios have declined.
Answer:
Poverty ratios have declined in:

1. East Asia and Pacific,
2. China,
3. Sub-Saharan Africa,
4. South Asia.

Question 2.
Identify the area of the globe which has the largest concentration of the poor.
Answer:
East Asia and the Pacific has the largest concentration of the poor.

JAC Class 9th Economics Poverty as a Challenge Textbook Questions and Answers  

Question 1.
Describe how the poverty line is estimated in India?
Answer:
A common method used to measure poverty is based on the income or consumption levels. A minimum level of food requirement, clothing, footwear, fuel and light, educational anu medical requirement, etc. are determined for subsistence while determining the poverty line in India. These physical quantities are multiplied by their prices in rupees.

The present formula for food requirement while estimating the poverty line is based on the desired calorie requirement. The accepted average calorie requirement in India is 2400 calories per person per day in rural areas and 2100 calories per person per day in urban areas.

Question 2.
Do you think that present methodology of poverty estimation is appropriate?
Answer:
No, we do not think that the present methodology of poverty estimation is appropriate. The present methodology of poverty estimation takes into consideration income and consumption level only. That is insufficient criterion. According to social scientists, poverty should be a looked at through some other indicators. These indicators may be lack of general resistance due to continuous malnutrition, lack of access to healthcare, lack of job opportunities, lack of access to safe drinking water and sanitation, etc. Poverty should also be viewed on the basis of social exclusion and vulnerability.

Question 3.
Describe poverty trends in India since 1973.
Answer:
There has been a substantial decline in poverty ratios in India. It was about 55 per cent in 1973-74, which reduced to 37 per cent in 2004-05. Although, the percentage of people living under poverty declined in the earlier two decades, i.e., 1973-1993, the number of poor declined from 407 million in 2004-05 to 270 million in 2011-12 with an average decline of 2.2 percentage points during 2004-05 to 2011-12.

The proportion of people below poverty line further came down to about 22 per cent in 2011-12. If the trend continues, people below poverty line may came down to less than 20 per cent in the next few years.

Question 4.
Discuss the major reasons for poverty in India.
Answer:
The major reasons for poverty in India are as follows:
1. Low level of Economic Development:
One historical reason is the low level of economic development under the British colonial administration. The policies of the colonial government ruined traditional handicrafts and discouraged development of industries like textiles.

2. Failure of Indian Administration:
The Indian administration failed at two fronts :
(i) Promotion of economic growth,
(ii) Population control which perpetuated the cycle of poverty.

3. Lack of Employment:
With the extension of irrigation and the advents of Green Revolution, many job opportunities were created in the agricultural sector but the effects were limited to some parts of India. The industries, both in the public and private sector did provide some jobs. But there were not enough to absorb all the job seekers.

4. Huge Income Inequalities:
This is one of the major reasons of poverty in India. Unequal distribution of land and other resources increases income inequalities.

Question 5.
Identify the social and economic groups which are most vulnerable to poverty in India.
Answer:
1. Social Groups:
The social groups more vulnerable to poverty are the scheduled caste and scheduled tribe households. These are not allowed to avail the facilities given to others due to the prevailing caste system. This leads to poverty.

2. Economic Groups:
The economic groups vulnerable to poverty are the rural agricultural labourer households and the urban casual labourer households. The rural agricultural labourers have no land of their own and are thus not able to earn enough to meet their daily needs, and hence remain poor.

Question 6.
Give an account of inter-state disparities of poverty in India.
Answer:
A major aspect of poverty in India is that the proportion of poor people is not the same in every state. The success rate of reducing poverty varies from state to state. Recent estimates show while the all India Head Count Ratio (HCR) was 21.9 per cent in 2011-12 states like Madhya Pradesh, Assam, Uttar Pardesh, Bihar and Odisha had higher poverty levels than the all, India poverty level. Bihar and Odisha continue to be the two poorest states with poverty ratios of 33.7 and 32.6 per cent respectively.

Along with rural poverty, urban poverty is also high in Odisha, Madhya Pradesh, Bihar and Uttar Pradesh. In comparison, there has been a significant decline in poverty in Kerala, Maharashtra, Andhra Pradesh, Tamil Nadu, Gujarat and West Bengal.

States like Punjab and Haryana have traditionally succeeded in reducing poverty with the help of high agricultural growth rates. Kerala with the help of human resource development, West Bengal with land reform measures, Andhra Pradesh and Tamil Nadu with Public distribution of food grains have been successful in reducing poverty levels.

Question 7.
Describe global poverty trends.
Answer:
The proportion of people in developing countries living in extreme economic poverty has fallen from 36 per cent in 1990 to 10 per cent in 2015. Although, there has been a substantial reduction in global poverty, it is marked with great regional differences.

Poverty declined substantially in China and South-East Asian countries as a result of rapid economic growth and massive investments in human resource development. Number of poor in China has come down from 88.3 per cent in 1981 to 14.7% per cent in 2008, and to 0.7 percent in 2015.

In the countries of South Asia (India, Pakistan, Sri Lanka, Nepal, Bangladesh, Bhutan), the decline has also been rapid-34 percent in 2005 to 16.2 percent in 2013. In Sub-Saharan Africa, poverty in fact declined from 51 per cent in 2005 to 41 per cent in 2015. In Latin America, the ratio of poverty has also declined from 10 percent in 2005 to 4 percent in 2015. Poverty has also resurfaced in some of the former socialist countries like Russia where officially it was non-existent earlier.

Question 8.
Describe the current government strategy of poverty allevaition.
Answer:
Removal of poverty has been one of the major objectives of Indian developmental strategy. The current anti-poverty strategy of the government is based broadly on two planks:
1. Promotion of Economic Growth:
Over a period of thirty years lasting upto the early eighties, there was little per capita income growth and not much reduction in poverty. Official poverty estimates which were about 45 percent in the early 1950s remained the same even in the early eighties.

Since the eighties, India’s economic growth has been one of the fastest in the world. The growth rate jumped from the average of about 3.5 per cent a year in the 1970s to about 6 per cent during the 1980s and 1990s. The higher growth rates have helped significantly in the reduction of poverty.

Therefore, it is becoming clear that there is a strong link between economic growth and poverty reduction. Economic growth widens opportunities and provides the resources needed to invest in human development. However, the poor may not be able to take direct advantage of the opportunities created by economic growth. Moreover, growth in the agriculture sector is much below the expectations.

2. Targetted Anti-poverty Programmes:
There is a clear need for targetted anti-poverty programmes. The government has implemented several anti- poverty schemes to eradicate poverty; Some of these are as follows :
(a) National Rural Employment Guarantee Act (NREG), 2005
(b) Prime Minister Rozgar Yojana (PMRY), 1993
(c) Rural Employment Generation Programme (REGP), 1995
(d) Swamajayanti Gram Swarozgar Yojana (SGSY), 1999
(e) Pradhan Mantri Gramodaya Yojana (PMGY), 2000
(f) Antyodaya Anna Yojana (AAY), 2000

Question 9.
Answer the following questions briefly:
1. What do you understand by human poverty?
Answer:
Human poverty is a concept that goes beyond the limited view of poverty as lack of income. It refers to the denial of political, economic and social opportunities to an individual, needed to maintain a reasonable standard of living. Illiteracy, lack of job opportunities, lack of access to proper healthcare and sanitation, caste and gender discrimination, etc are all components of human poverty.

2. Who are the poorest of the poor?
Answer:
Women, elderly people and female infants are the poorest of the poor in society Women, elderly people and the girl child are systematically denied equal access to the resources available in the family. That is why they are considered as the poorest of the poor.

3. What are the main features the National Rural Employment Guarantee Act, 2005?
Answer:
National Rural Employment Guarantee Act, 2005 was passed in September 2005.

Its main features are as under:

1. The Act provides 100 days assured employment every year to every rural household.
2. One-third of the proposed jobs would be reserved for women.
3. Under the programme, if an applicant is not provided employment within fifteen days he/she will be entitled to get daily unemployment allowance.
4. The central government and state governments will establish National Employment Guarantee Funds and State Employment Guarantee Funds respectively.

JAC Class 9 Social Science Solutions

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 12 Heron’s Formula Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 12 Heron’s Formula

Question 1.
The area of a triangle is 30 cm². Find the base if the altitude exceeds the base by 7 cm.

Solution :
Let base BC = x cm
Then altitude = (x + 7) cm
Area of ΔABC = \(\frac {1}{2}\) × base × height
⇒ 30 = \(\frac {1}{2}\)(x)(x + 7)
⇒ 60 = x² + 7x
⇒ x² + 7x – 60 = 0
⇒ x² + 12x – 5x – 60 = 0
⇒ x(x + 12) – 5(x + 12) = 0
⇒ (x – 5)(x + 12) = 0
⇒ x = 5 or x = -12+
⇒ x = 5 [∵ x ≠ -12]
∴ Base (x) = 5 cm and
Altitude = x + 7 = 5 + 7 = 12 cm.

Question 2.
The cost of turfing a triangular field at the rate of ₹ 45 per 100 m² is ₹ 900. Find the height, if double the base of the triangle is 5 times the height.
Solution :
Let the height of triangular field be h metres.
It is given that 2 × (base) = 5 × (Height)
∴ Base = \(\frac {5}{2}\) h
Area = \(\frac {1}{2}\) × Base × Height
Area = \(\frac {1}{2}\) × \(\frac {5}{2}\)h × h = \(\frac {5}{4}\)h²m² …………(i)
∴ Cost of turfing the field is ₹ 45 per 100m²
∴ Area = Total cost / Rate per sq.m
= \(\frac{900}{45 / 100}=\frac{90000}{45}\)
= 2000 m² …………(ii)
From (i) and (ii), we get
\(\frac {5}{4}\)h² = 2000
⇒ 5h² = 8000
⇒ h² = 1600
⇒ h = 40 m
∴ Height of the triangular field is 40 m.

Question 3.
From a point in the interior of an equilateral triangle, perpendicular drawn to the three sides are 8 cm, 10 cm and 11 cm respectively. Find the area of the triangle.

Solution :
Let each side of the equilateral ΔABC = x cm,
From an interior point O, OD, OE and OF perpendiculars be drawn to BC, AC and AB respectively.
It is given that OD = 11 cm, OE = 8 cm and OF = 10 cm.
Join OA, OB and OC.
Area of ΔABC = Area of ΔOBC + Area of ΔOCA + Area of ΔOAB
= \(\frac {1}{2}\) × 11 + \(\frac {1}{2}\) × 8 + \(\frac {1}{2}\) × 10 = \(\frac {29}{2}\) × cm²
But, area of an equilateral triangle, whose each side is x = \(\frac{\sqrt{3}}{4}\) x²cm²
Therefore,
\(\frac{\sqrt{3}}{4}\) x² = \(\frac {29}{2}\)x
∴ x = \(\frac{4 \times 29}{2 \times \sqrt{3}}=\frac{58}{\sqrt{3}}\) cm
∴ Area of ΔABC
= \(\frac{29}{2} \times \frac{58}{\sqrt{3}}\) cm² = \(\frac{\sqrt{841}}{1.73}\)cm²
∴ Area of ΔABC = 486.1 cm²

Question 4.
The difference between the sides at right angles in a right-angled triangle is 14 cm. The area of the triangle is 120 cm². Calculate the perimeter of the triangle.
Solution :
Let the sides containing the right angle be x cm and (x – 14) cm.
Then, its area = [\(\frac {1}{2}\).x. (x – 14)] cm²
But, area = 120 cm² [Given]
∴ \(\frac {1}{2}\)x (x – 14) = 120
⇒ x² – 14x – 240 = 0
⇒ x² – 24x + 10x – 240 = 0
⇒ x(x – 24) + 10 (x – 24) = 0
⇒ (x – 24) (x + 10) = 0
⇒ x = 24 [Neglecting x = -10]
∴ One side = 24 cm,
other side = (24 – 14) cm = 10 cm
Hypotenuse
= \(\sqrt{(24)^2+(10)^2}\) cm
= \(\sqrt{576+100}\) cm
= \(\sqrt{676}\) cm = 26 cm.
∴ Perimeter of the triangle
= (24 + 10 + 26) cm = 60 cm.

Question 5.
Find the percentage increase in the area of a triangle if its each side is doubled.
Solution :
Let a, b, c be the sides of the given triangle and s be its semi-perimeter
∴ s = \(\frac {1}{2}\)(a + b + c) …………(i)
The sides of the new triangle are 2a, 2b and 2c. Let s’ be its semi-perimeter.
∴ s’ = (2a + 2b + 2c)
= a + b + c = 2s [Using (i)]
Let Δ = Area of given triangle
Δ = \(\sqrt{s(s-a)(s-b)(s-c)}\) …….(ii)
And, Δ’ = Area of new triangle
Δ’ = \(\sqrt{s^{\prime}\left(s^{\prime}-2 a\right)\left(s^{\prime}-2 b\right)\left(s^{\prime}-2 c\right)}\)
= \(\sqrt{2 s(2 s-2 a)(2 s-2 b)(2 s-2 c)}\)
= \(\sqrt{16 s(s-a)(s-b)(s-c)}\)
Δ’ = 4Δ
∴ Increase in the area of the triangle
= Δ’ – Δ = 4Δ – Δ = 3Δ
∴ % increase in area = (\(\frac {3Δ}{Δ}\) × 100)%
= 300%

Multiple Choice Questions

Question 1.
The area of the field ABGFEA is:

(a) 7225 m²
(b) 7230 m²
(c) 7235 m²
(d) 7240 m²
Solution :
(a) 7225 m²

Question 2.
Area of shaded portion as shown in the figure is:

(a) 12 m²
(b) 13 m²
(c) 14 m²
(d) 15 m²
Solution :
(a) 12 m²

Question 3.
The lengths of four sides and a diagonal of the given quadrilateral are indicated in the diagram. If A denotes the area of quadrilateral in cm², then A is

(a) 12\(\sqrt{6}\) sq. unit
(b) 6 sq. unit
(c) 6\(\sqrt{6}\) sq. unit
(d) \(\sqrt{6}\) sq. unit
Solution :
(a) 12\(\sqrt{6}\) sq. unit

Question 4.
If the sides of a triangle are doubled, then its area:
(a) Remains the same
(b) Becomes doubled
(c) Becomes three times
(d) Becomes four times
Solution :
(d) Becomes four times

Question 5.
Inside a triangular garden there is a flower bed in the form of a similar triangle. Around the flower bed runs a uniform path of such a width that the side of the garden are double of the corresponding sides of the flower bed. The areas of the path and the flower bed are in the ratio:
(a) 1 : 1
(b) 1 : 2
(c) 1 : 3
(d) 3 : 1
Solution :
(d) 3 : 1

JAC Board Class 9th Social Science Important Questions Civics Chapter 1 What is Democracy? Why Democracy?

I. Objective Type Questions

1. Democracy is a form of government in which the rulers are elected by:
(a) the people
(b) rich people
(c) the king
(d) all of the above.
Answer:
(a) the people

2. In which year, General Pervez Musharraf held a referendum which granted him five years’ extension as a President?
(a) 2005
(b) 2008
(c) 2002
(d)2010.
Answer:
(c) 2002

3. Since its independence in, Mexico holds elections after every six years to elect its President.
(a) 1938
(b) 1930
(c) 1935
(d) 1947.
Answer:
(b) 1930

4. Which form of government requires all citizens to take part in politics ?
(a) Democracy
(b) Monarchy
(c) Dictatorship
(d) None of these.
Answer:
(a) Democracy

5. Democracy is better than other forms of government because:
(a) people are given opportunities to participate directly in government
(b) democratic governments prepare annual budget
(c) it is a more accountable form of government
(d) none of the above.
Answer:
(c) it is a more accountable form of government

II. Very Short Answer Type Questions

Question 1.
State the definition of democracy given by Abraham Lincoln.
Answer:
Abraham Lincoln, the President of the United States from 1861 to 1865, defined democracy as “Government of the people, for the people and by the people.”

Question 2.
From which Greek word democracy has been derived?
Answer:
Democracy has been derived from the Greek word ‘Democratia’.

Question 3.
What do you mean by the term ‘Democracy’?
Answer:
The term democracy is derived from two Greek words ‘Demos’ which means people and ‘Kratia’ ‘meaning the government. Thus, Democracy means “Rule by the people”.

Question 4.
Which Pakistani general led a military coup in October 1999?
Answer:
The Pakistani general who led a military coup in October 1999 was General Pervez Musharaf.

Question 5.
What was the designation taken by General Pervez Musharraf for himself when he overthrew the democratic government of Pakistan in 1999?
Answer:
General Pervez Musharraf declared himself the chief executive of Pakistan when he overthrew the democratic government of Pakistan in 1999.

Question 6.
What is a Referendum?
Answer:
A Referendum is a vote in which the electorate can express a view on a particular issue of public policy.

Question 7.
With what motive did General Pervez Musharraf issue a ‘legal framework order’ in August 2002?
Answer:
The motive was to ensure that he had the ultimate power to decide how he wanted Pakistan to be ruled.

Question 8.
Mention one of the important features of democracy.
Answer:
One important feature of democracy is that the final decision-making power rests with those elected by the people.

Question 9.
What is the name of the Chinese parliament?
Answer:
The name of the Chinese parliament is Quanguo Renmin Daibiuo Dahui (National People’s Congress).

Question 10.
Which party always forms the government in China?
Answer:
The Communist Party of China always forms the government in China.

Question 11.
When did Mexico get independence?
Answer:
Mexico got independence in 1930.

Question 12.
From 1930, which country holds elections after every six years and which has never been under a military or dictator rule?
Answer:
Mexico.

Question 13.
What is the name of famous political party of Mexico?
Answer:
The famous political party of Mexico is Institutional Revolutionary Party (PRI).

Question 14.
Despite having an elected parliament and government under the monarchy and military rule, why can’t they be called democracy?
Answer:
Because the elected Parliament is nominal. Real power rests in the hands of those people, whom the people have not chosen.

Question 15.
Who should have the final decision-making power in a democracy?
Answer:
The power to make the final decisions in a democracy should be in the hands of the elected representatives by the people.

Question 16.
What do you understand by political equality?
Answer:
Political equality means that each adult citizen must have one vote and each vote must have one value.

Question 17.
When did Zimbabwe get independence?
Answer:
Zimbabwe gained independence inl980.

Question 18.
Which party of Zimbabwe led the struggle for independence?
Answer:
ZANU-PF.

Question 19.
What does the example of Zimbabew tell us?
Answer:
The example of Zimbabew shows that popular approval of the rulers is necessary in a democracy.

Question 20.
Within what limits does a democratic government govern?
Answer:
A democratic government rules within limits set by constitutional law and citizens’ rights.

Question 21.
State any two characteristics of democracy.
Answer:

1. Rulers elected by the people take all the major decisions.
2. Elections offer a choice and fair opportunity to the people to change the current rulers.

Question 22.
Give any two arguments against democracy.
Answer:

1. Leaders keep changing in a democracy. This leads to instability.
2. Democracy leads to corruption.

Question 23.
Give any two arguments for democracy.
Answer:

1. It is a more accountable form of government.
2. It improves the quality of decision-making.

Question 24.
Which governance system is based on the principle of political equality?
Answer:
Democratic governance is based on the principle of political equality.

Question 25.
Mention any four challenges to Democracy.
Answer:

1. Economic Inequalities,
2. Social Inequalities,
3. Leadership and Political Parties,
4. Power-play in ‘Elections’.

III. Short Answer Type Questions

Question 1.
How did Musharraf establish his rule in Pakistan?
Answer:
General Pervez Musharraf led a military coup in Pakistan in October 1999. He over-threw a democratically-elected government and declared himself the chief executive of the country. Later, he changed his designation to President. In 2002, he held a refrendum in the country that granted him a five-year extension.

In August, 2002, he issued a legal framework order that amended the constitution of Pakistan. According to this order, the President can dismiss the national or provincial assemblies. After passing the ‘legal framework order’ elections were held to the national and state assemblies. But the final power was in the hands of military officers and General Musharraf. Elected representatives had only some powers.

Question 2.
“In Pakistan people elect their representatives to the national and provincial assemblies but still it cannot be called a democratic country.” Give reasons.
Answer:
In Pakistan, General Parvez Musharraf led a military coup against a democratically- elected government. The work of the civilian cabinet was supervised by a National Security Council which was dominated by military officers. Though, at present, Pakistan has a democratic government under the leadership of Imran Khan, but the government is still a tool in the hands of Pakistani Army and ISI.

Question 3.
“In China, elections are regularly held after 5 years for electing the country’s Parliament, but still it cannot be called a democratic country.” Give reasons.
Answer:
In China, elections are regularly held after every five years for electing the country’s Parliament. Before contesting elections, a candidate needs the approval of theChinese Communist Party. Only those who are the members of the Chinese Communist Party or eight smaller parties allied to it are allowed to contest elections. The government is always formed by the Communist Party. Therefore, China cannot be called a democratic country.

Question 4.
‘Since its independence in 1930, Mexico holds elections after every six years to elect its President. The country has never been under a military or dictator’s rule but still it cannot be called a democratic country’. Give reasons.
Answer:
Since its independence in 1930, Mexico holds elections after every 6 years. The country has never been under a dictator or military ruler. But until 2000 every election was won by a party called PRI (Institutional Revolutionary Party). Opposition parties did contest elections, but never managed to win. The government used all its machinery to win elections.

All those who were employed in goverment offices had to attend its party meeting. Teachers of government schools used to force parents to vote for the PRI. Media used to work under the influence of the government. The PRI spent a large sum of money in the campaign for its condidates. Thus, due to lack of free and fair elections, Mexico cannot be called a democratic country.

Question 5.
Why are Saudi Arabia, Estonia and China non-democratic countries though they declare themselves as democracies ? State one reason for each of the countries.
Answer:
One major demand of democracy is ‘universal adult franchise’, i.e., the right to vote for every adult citizen. But in world politics, there are many instances of denial of equal right to vote.
These are:

1. In Saudi Arabia, women did not have the right to vote until 2015.
2. Estonia made its citizenship rules in such a manner that people be longing to Russian minority find of it difficult to get the right to vote.
3. In China, before contesting the election, the candidate needs the approval of the Chinese Communist Party. Although these countries declare themselves as democracies, the fundamental principle of ‘political equality’ is denied in all the cases. Thus, these are not truly democratic countries.

Question 6.
Why Zimbabwe cannot be called a democratic nation? Give reasons.
Answer:
Since independence in 1980, the country has been ruled by ZANU-PF. Its leader, Robert Mugabe, had been ruling the country since independence. Elections have been held regularly and always won by ZANU-PF. President Mugabe uses unfair practices in elections.

Over the years, his government has changed the constitution several times to increase the powers of the President. Opposition party workers are harassed and their meeting disrupted. Public protests and demonstrations against the government are declared illegal. The courts are there, but most of the time their orders are ignored by the government. Because of all these reasons, Zimbabwe can¬not be called a democratic country.

Question 7.
Which three rights should every citizen of a democratic country get?
Answer:
Following are the three rights should every citizen of a democratic country get

1. Citizens should be free to express their opinion in public, to form associations, to protest and take other political actions.
2. They should be equal in the eyes of the law.
3. These rights must be protected by an independent judiciary, whose orders should be obeyed by everyone.

Question 8.
Explain the major arguments against democracy.
Answer:
The major arguments against democracy are as follows:

1. Leaders keep changing in a democracy. This leads to instability.
2. Democracy is all about political competition and power-play. There is no scope for morality.
3. Elected leaders do not know the best interest of the people. It leads to bad decisions.
4. Democracy leads to corruption, for it is based on electoral competition.
5. Ordinary people don’t know what is good for them; they should not decide anything.

Question 9.
“Democracy improves the quality of decision-making.” Explain.
Answer:
Democracy is based on consultation and discussion.

1. A democratic decision always involves many persons’ discussions and meetings. When a number of people put their heads together, they are able to point out the possible mistakes in any decision.
2. As most of the decisions are taken by discussion, this reduces the chances of irrational or irresponsible decisions.
3. If the decision is not according to the wishes of the people they have the right to protest and they can even force the government to withdraw it.
4. Thus, we can say that democracy improves the quality of decision-making.

Question 10.
“Democracy provides a method to deal with differecences and conflicts.” Explain.
Answer:

1. Democracy provides all the citizens some basic rights through which they can give their opinion.
2. Democracy provides the citizens a right to choose their representatives and change them if they do not work according to their wishes.
3. In the parliament, all the members have the right to give their opinion. Therefore, we can say that democracy provides a method to deal with differences and conflicts.

Question 11.
“Democracy is better than other forms of government because it allows us to correct its own mistakes.” Explain.
Answer:
There is no guarantee that mistakes cannot be made in democracy. No form of government can guarantee that. The advantage in a democracy is that such mistakes cannot be hidden for long. There is a space for public discussion on these mistakes and there is a room for correction. Either the rulers have to change their decisions or the rulers can be changed. While this cannot happen in a non-democratic government.

Question 12.
What is democracy? Which are its four features?
Answer:
Democracy is a form of government in which the rulers are elected by the people. Some features of democracy are:

1. Democracy is a form of government in which the rules are elected by the people.
2. A democracy must be based on a free and fair election, where those currently in power have a fair chance of losing.
3. In a democracy, each adult citizen must have one vote and each vote must have one value.
4. In a democracy, government rulers within limits set by constitutional law and citizens’ rights.

Question 13.
Keeping in mind the features and principles of democracy, can you say that India is a democratic country? Explain by giving examples.
Answer:

1. Decision-making power with the people’s representative: In India, the final decision-making power is with the parliament, whose members are directly elected by the people.
2. Free and fair elections: In India, we have the Election Commision an independent body for conducting elections. Due to this, the party which is in power has a fair chance of losing.
3. One person, one vote, one value: In India, all the adult citizens have one vote and each vote has one value.
4. Rule of law and respect for rights: Indian government rules within limits set up by the constitutional law. All the citizens have been given some basic rights.

Question 14.
Why is democracy better than any other form of government? Write any five argument to support your answer.
Or
Explain any five arguments in favour of democracy.
Answer:
Democracy is better than any other form of government Five arguments in favour of democracy are as follows:

1. A democratic form of government is a better government because it is a more accountable form of government. A democracy requires that the rulers have to attend to the needs of the people.
2. Democracy is based on consulation and discussion. Although it takes time, this process reduces the chances of irrational and irresponsible decisions. Thus, democracy improves the quality of decision-making.
3. Democracy provides a method to deal with differences and conflicts in the society. In a diverse country like India, democracy keeps our country united.
4. As democracy is based on the principle of political equality, it enhances the dignity of citizens.
5. Democracy is better than other forms of government because it allows us to correct our own mistakes. In democracy, there is a space for public discussion on these mistakes and there is always a room for correction.

Question 15.
“Democracy enhances the dignity of citizens”. Explain.
Answer:
There is no guarantee that mistakes cannot be made in democracy. No form of government can guarantee that. The advantage in a democracy is that such mistakes cannot be hidden for long. There is a space for public discussion on these mistakes and there is always a room for correction. Either the rulers have to change their decisions or the rulers can be changed. While this cannot happen in a non-democratic government.

Question 16.
Democracy is based on the principle of political equality. Explain.
Answer:
Democracy is based on the principle of political equality due to the recognition that the poor and the least educated have the same status as the rich and the educated. People are not subjects of a ruler, they are the rulers themselves. Even when they make mistakes, they are responsible for their conduct.

Question 17.
Democracy is the government of the people, for the people and by the people. Explain it.
Answer:
Democracy is a form of government in which the rulers are elected by the people. Rulers elected by the people take all the important decisions. The rulers of democracy have to attend to need of the people. Democracy is based on discussion and consultation.

A democratic decision always involves many persons, discussions and meetings. So, democracy improves the quality of decision-making. Democracy recognises the principal of political equality. It recognises that the poor and the least educated have the same status as the rich and the educated. Thus, people are not subjects of a ruler, they are the rulers themselves.

III. Long Answer Type Questions

Question 1.
Explain any five drity tricks used by the Institutional Revolutionary Party (PRI) to win elections in Mexico.
Answer:
The Institutional Revolutionary Party (PRI) of Mexico won all the elections from 1930 till 2000. The opposition parties did contest elections, but never managed to win. The PRI used may dirty triks to win the election. These were:

1. All those who were employed in government offices had to attend its party meetings.
2. Teachers of government schools used to force the parents to’vote for the Institutional Revolutionary Party.
3. Sometimes, the polling booths were shifted from one place to another without prior notice, which made it difficult for people to cast their votes.
4. Media largely ignored the activities of the opposition political parties.
5. Being in power, the PRI spent a large sum of money to manipulate the elections and in campaigning for the candidates.

Question 2.
Explain the major features of democracy.
Answer:
The major features of democracy are as follows:
1. Responsible Government:
A democratic government is a responsible govern¬ment. The reprsentatives elected by the people on the basis of universal adult franchise remain responsible to the people, and in case they do not remain responsible before the people, the people can change them during the next elections.

2. Free and fair elections:
A democracy is based on free and fair elections, where those currently in power have a fair chance of losing.

3. Based on Liberty and Fraternity:
In democracy, the rights and the liberty of the people are well safe guarded. People are given freedom to express their views without any fear. They can criticise the wrong policies of the government.

4. Respect of the Principle of Equality:
In a democracy, all are equal in the eyes of law, and no discrimination is done on the basis of birth, race, caste, colour, sex, religion, etc. All citizens get equal opportunities to participate in the affairs of the state.

5. Government based on the will of the people:
A democracy is based on the will of the people, and it functions according to their consent. The government cannot ignore the interest of the people.

6. Political Education:
The gretaest merit of a democracy is its educative value. Participation in elections and other political activities, make the people intelligent and politically conscious. They become enlightened citizens.

Question 3.
Explain any five limitations of democracy.
Answer:

1. Instability: Under democracy, leaders and political parties keep changing. This leads to political inslability.
2. Law morality: Democracy is all about political competition and power-play. There is no scope for morality.
3. Delays in decision-making: All the decisions are to be approved and discussed in the Parliament, and many people and institutions are to be consulted. So, it leads to delays in decision-making.
4. Bad decisions: As most of the leaders do not know the best interest of the people, it leads to bad decisions.
5. Corruption: As democracy is based on electoral competition, it leads to corrup¬tion. Many political parties used muscle and money power to come to power.
6. Illiterate and politically unconscious voters: In most of the developing countries, voters are illiterate and politically unconscious, so they elect wrong governance.

Question 4.
Distinguish between democratic and non-democratic conditions.

Democratic	Non-Democratic
1. Government: A democratic government is elected by the people and it works for the people. It is also answerable to the people. People can change it, if it is not working according to the wishes of the people.	1. Government: A non-democratic government is not elected by the people. The ruler may be hereditary or a military general, who has come to power by force. People cannot change it as there are no regular elections.
2. Basic rights: Under democracy, people ( are given basic rights like freedom of speech, freedom of movement, freedom of forming associations or unions, etc.	2. No basic rights: Under non-democratic conditions, peoploe are not given basic rights. Citizens are put behind bars if they try to demand the basic rights.
3. Regular elections: Under this, there (i are regular elections through which people can change their government.	3. No regular elections: Under this, there are no regular elections. Most of the non-democratic rulers have captured the power through military coup.
4. Constitution: Under democracy, the; (i government works within the limits, set up by the constitution. It has different institutions like judiciary which can check the powers of the government. Parliament is supreme 1 Under ( democracy, it is the parliament which is supreme. All the leaders or’ even the govenment is answerable to the parliament.	4. Constitution: Some of the non democratic countries may have a constitution, but it can be changed only according to the wishes of the dictator.
5. Parliament is supreme: Under democracy, it is the parliament which is supreme. All the leaders or’ even the govenment is answerable to the parliament.	5. The ruler is supreme: Under non-democratic conditions, it is the ruler who is supreme. All the political and economi powers are in his/her hand.

 

JAC Class 9 Social Science Important Questions

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 15 Probability Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 15 Probability

Question 1.
A card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting
(i) A king.
(ii) A heart.
(iii) A seven of heart.
(iv) A jack, queen or a king.
(v) A two of heart or a two of diamond.
(vi) A face card.
(vii) A black card.
(viii) Neither a heart nor a king,
(ix) Neither an ace nor a king.
Solution :
Total number of outcomes = 52
(i) A king
No. of kings = 4
P(A) = \(\frac{4}{52}=\frac{1}{13}\)

(ii) A heart, P(A) = \(\frac{13}{52}=\frac{1}{4}\)

(iii) A seven of heart P(A) = \(\frac{1}{52}\)

(iv) A jack, queen or a king,
P(A) = \(\frac{12}{52}=\frac{3}{13}\)

(v) A two of heat or a two of diamond,
P(A) = \(\frac{2}{52}=\frac{1}{26}\)

(vi) A face card, P(A) = \(\frac{12}{52}=\frac{3}{13}\)

(vii) A black card, P(A) = \(\frac{26}{52}=\frac{1}{2}\)

(viii) Neither a heart nor a king (13 heart + 4 king, but 1 common)
P(A) = 1 – \(\frac{16}{52}=\frac{52-16}{52}=\frac{36}{52}=\frac{9}{13}\)

(ix) Neither an ace nor a king,
P(A) = \(\frac{44}{52}=\frac{11}{13}\)

Question 2.
Two coins are tossed simultaneously. Find the probability of getting
(i) two heads
(ii) at least one head
(iii) no head
Solution :
On tossing two coins simultaneously, all the possible outcomes are HH, HT, TH, TT.
(i) The probability of getting two heads
= P (HH)
= No. of outcomes of two heads / Total no. of possible outcomes
= \(\frac {1}{4}\)

(ii) The probability of getting at least one head
= No. of favourable outcomes / Total no. of outcomes
= \(\frac {3}{4}\)

(iii) The probability of getting no head
P(TT) = \(\frac {1}{4}\)

Question 3.
A bag contains 5 red balls, 8 white balls, 4 green balls and 7 black balls. If one ball is drawn at random, find the probability that it is
(i) Black
(ii) Not red
(iii) Green
Solution :
Number of red balls in the bag = 5.
Number of white balls in the bag = 8.
Number of green balls in the bag = 4.
Number of black balls in the bag = 7.
∴ Total number of balls in the bag = 5 + 8 + 4 + 7 = 24.
Drawing balls randomly are equally likely outcomes.
∴ Total number of possible outcomes = 24.
Now,
(i) There are 7 black balls, hence the number of such favourable outcomes = 7
∴ Probability of drawing a black ball
= No. of favourable outcomes / Total no. of possible outcomes
= \(\frac {7}{24}\)

(ii) There are 5 red balls, hence the number of such favourable outcomes = 5.
∴ Probability of drawing a red ball
= No. of favourable outcomes / Total no. of possible outcomes
= \(\frac {5}{24}\)
∴ Probability of drawing not a red ball = P(Not red ball) = 1 – \(\frac{5}{24}=\frac{19}{24}\)

(iii) There are 4 green balls.
∴ Number of such favourable outcomes = 4
Probability of drawing a green ball = No. of favourable outcomes / Total no. of possible outcomes
= \(\frac{4}{24}=\frac{1}{6}\)

Question 4.
A card is drawn from a well-shuffled deck of playing cards. Find the probability of drawing
(i) a face card
(ii) a red face card
Solution :
Random drawing of cards ensures equally likely outcomes
(i) Number of face cards (King, Queen and jack of each suits) = 4 x 3 = 12.
Total number of cards in deck = 52.
∴ Total number of possible outcomes = 52.
P (drawing a face card) = \(\frac{12}{52}=\frac{3}{13}\)

(ii) Number of red face cards = 2 × 3 = 6.
Number of favourable outcomes of drawing red face card = 6.
P(drawing of red face card) = \(\frac{6}{52}=\frac{3}{26}\)

Multiple Choice Questions

Question 1.
3 Coins are tossed simultaneously. The probability of getting at least 2 heads is
(a) \(\frac {3}{10}\)
(b) \(\frac {3}{4}\)
(c) \(\frac {3}{8}\)
(d) \(\frac {1}{2}\)
Solution :
(c) \(\frac {3}{8}\)

Question 2.
Two cards are drawn successively with replacement from a pack of 52 cards. The probability of getting two aces is
(a) \(\frac {1}{169}\)
(b) \(\frac {1}{221}\)
(c) \(\frac {1}{265}\)
(d) \(\frac {1}{663}\)
Solution :
(b) \(\frac {1}{221}\)

Question 3.
In a single throw of two dice, the probability of getting a sum of more than 7 is
(a) \(\frac {7}{36}\)
(b) \(\frac {7}{12}\)
(c) \(\frac {5}{12}\)
(d) \(\frac {5}{36}\)
Solution :
(c) \(\frac {5}{12}\)

Question 4.
Two cards are drawn at random from a pack of 52 cards. The probability that both are the cards of spade is
(a) \(\frac {1}{26}\)
(b) \(\frac {1}{4}\)
(c) \(\frac {1}{17}\)
(d) None of these
Solution :
(c) \(\frac {1}{17}\)

Question 5.
Two dice are thrown together. The probability that sum of the two numbers will be a multiple of 4 is
(a) \(\frac {1}{9}\)
(b) \(\frac {1}{3}\)
(c) \(\frac {1}{4}\)
(d) \(\frac {5}{9}\)
Solution :
(c) \(\frac {1}{4}\)

Question 6.
If the three coins are simultaneously tossed compute the probability of 2 heads coming up.
(a) \(\frac {3}{8}\)
(b) \(\frac {1}{4}\)
(c) \(\frac {5}{8}\)
(d) \(\frac {3}{4}\)
Solution :
(a) \(\frac {3}{8}\)

Question 7.
A coin is tossed successively three times. The probability of getting one head or two heads is:
(a) \(\frac {2}{3}\)
(b) \(\frac {3}{4}\)
(c) \(\frac {4}{9}\)
(d) \(\frac {1}{9}\)
Solution :
(b) \(\frac {3}{4}\)

Question 8.
One card is drawn from a pack of 52 cards. What is the probability that the drawn card is either red or king:
(a) \(\frac {15}{26}\)
(b) \(\frac {1}{2}\)
(c) \(\frac {7}{13}\)
(d) \(\frac {17}{32}\)
Solution :
(c) \(\frac {7}{13}\)

Jharkhand Board JAC Class 9 Maths Solutions Chapter 14 Statistics Ex 14.3 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 14 Statistics Ex 14.3

Page-258

Question 1.
A survey conducted by an organisation for the cause of illness and death among the women between the ages 15 – 44 (in years) worldwide, found the following figures (in %):

S.No	Causes	Female fatality rate (%)
1.	Reproductive health conditions	31.8
2.	Neuropsychiatric conditions	25.4
3.	Injuries	12.4
4.	Cardiovascular conditions	4.3
5.	Respiratory conditions	4.1
6.	Other causes	22.0

(i) Represent the information given above graphically.
(ii) Which condition is the major cause of women’s ill health and death worldwide?
(iii) Try to find out, with the help of your teacher, any two factors which play a major role in the cause in (ii) above being the major cause.
Answer:
(i) The data is represented below graphically.

(ii) From the above graphical data, we observe that reproductive health conditions is the major cause of womens ill health and death worldwide.
(iii) Two factors responsible for cause in (ii)

• Lack of proper care and under-standing.
• Lack of medical facilities.

Question 2.
The following data on the number of girls (to the nearest ten) per thousand boys in different sections of Indian society is given below.

Section	Number of girls per thousand boys
Scheduled Caste (SC)	940
Scheduled Tribe (ST)	970
Non SC/ST	920
Backward districts	950
Non backward districts	920
Rural	930
Urban	910

(i) Represent the information above by a bar graph.
(ii) In the classroom discuss what conclusions can be arrived at from the graph.
Answer:
(i)

(ii) It can be observed from the above graph that the maximum number of girls per thousand boys is in ST. Also, the backward districts and rural areas have more number of girls per thousand boys than non¬backward districts and urban areas.

Page-259

Question 3.
Given below are the seats won by different political parties in the polling outcome of a state assembly elections:

Political party	A	B	C	D	E	F
Seats won	75	55	37	29	10	37

(i) Draw a bar graph to represent the polling results.
(ii) Which political party won the maximum number of seats?
Answer:
(i)

(ii)The party named A has won the maximum number of seats.

Question 4.
The length of 40 leaves of a plant are measured correct to one millimetre, and the obtained data is represented in the following table :

Length (in mm)	Number of leaves
118 – 126	3
127 – 135	5
136 – 144	9
145 – 153	12
154 – 162	5
163 – 171	4
172 – 180	2

(i) Draw a histogram to represent the given data. [Hint: First make the class intervals continuous]
(ii) Is there any other suitable graphical representation for the same data?
(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long? Why?
Answer:
(i) The data is represented in a discontinuous class interval. So, first we will make it continuous.
The difference is 1, so we subtract \(\frac{1}{2}\) = 0.5 from lower limit and add 0.5 to the upper limit.

Length (in mm)	Number of leaves
117.5 – 126.5	3
126.5 – 135.5	5
135.5 – 144.5	9
144.5 – 153.5	12
153.5 – 162.5	5
162.5 – 171.5	4
171.5 – 180.5	2

(ii) Yes, the data can also be represented by frequency polygon.
(iii) No, it is incorrect to conclude that the maximum number of leaves are 153 mm long because maximum number of leaves are lying between the length of 144.5-153.5.

Question 5.
The following table gives the life times of 400 neon lamps:

Number of lamps	Lifetime (in hours)
300 – 400	14
400 – 500	56
500 – 600	60
600 – 700	86
700 – 800	74
800 – 900	62
900 – 1000	48

(i) Represent the given information with the help of a histogram.
(ii) How many lamps have a life time of more than 700 hours?
Answer:
(i)

(ii) 74 + 62 + 48 = 184 lamp’s have a life time of more than 700 hours.

Page-260

Question 6.
The following table gives the distribution of students of two sections according to the marks obtained by them:

Section A		Section B
Marks	Frequency	Marks	Frequency
0-10	3	0-10	5
10-20	9	10-20	19
20-30	17	20-30	15
30-40	12	30-40	10
40-50	9	40-50	1

Represent the marks of the students of both the sections on the same graph by
two frequency polygons. From the two polygons compare the performance of the two sections.
Answer:
The class mark can be found by (Lower limit + Upper limit)/2.
For section A

Section A
Marks	Frequency
0-10	3
10-20	9
20-30	17
30-40	12
40-50	9

For section B

Section B
Marks	Frequency
0-10	5
10-20	19
20-30	15
30-40	10
40-50	1

Now, we draw frequency polygons for the given data.

In the two polygons, we observed that most of the students of section A got higher marks. So the result of section A is better.

Question 7.
The runs scored by two teams A and B on the first 60 balls in a cricket match are given below:

Number of balls	Team A	Team B
1 – 6	2	5
7 – 12	1	6
13 – 18	8	2
19 – 24	9	10
25 – 30	4	5
31 – 36	5	6
37 – 42	6	3
43 – 48	10	4
49 – 54	6	8
55 – 60	2	10

Represent the data of both the teams on the same graph by frequency polygons.
[Hint: First make the class intervals continuous.]
Answer:
The data given in the form of discontinu¬ous class intervals. So, first we will make them continuous. The difference is 1, so
we subtract \(\frac{1}{2}\) = 0.5 from lower limit and add 0.5 to the upper limit.

Number of balls	Class Marks	Team A	Team B
0.5 – 6.5	3.5	2	5
6.5 – 12.5	9.5	1	6
12.5 – 18.5	15.5	8	2
18.5 – 24.5	21.5	9	10
24.5 – 30.5	27.5	4	5
30.5 – 36.5	33.5	5	6
36.5 – 42.5	39.5	6	3
42.5 – 48.5	45.5	10	4
48.5 – 54.5	51.5	6	8
54.5 – 60.5	57.5	2	10

Now, we draw frequency polygons for the given data.

Page-261

Question 8.
A random survey of the number of children of various age groups playing in a park was found as follows:

Age (in years)	Number of children
1 – 2	5
2 – 3	3
3 – 5	6
5 – 7	12
7 – 10	9
10 – 15	10
15 – 17	4

 

Draw a histogram to represent the data above.
Answer:
The class intervals in the data is having varying width. We know that the area of rectangle is proportional to the frequencies in the histogram. The class interval with minimum class size 1 is selected and the length of the rectangle is proportionate to it.

Taking the age of children on x-axis and no. of children on v-axis, the histogram can be drawn as follows.

Question 9.
100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:

Number of letters	Number of surnames
1 – 4	6
4 – 6	30
6 – 8	44
8 – 12	16
12 – 20	4

 

(i) Draw a histogram to depict the gi ven information.
(ii) Write the class interval in which the maximum number of surnames lie.
Answer:
(i) The class intervals in the data is having varying width. We know that the area of rectangle is proportional to the frequencies in the histogram. The class interval with minimum class size 2 is selected and the length of the rectangle is proportionate to it.


(ii) The class interval in which the maximum number of surnames lie is 6-8.

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 14 Statistics Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 14 Statistics

Question 1.
The marks obtained by 40 students of class IX in a mathematics test are given below:
18, 55, 68, 79, 85, 43, 29, 68, 54, 73, 47, 35, 72, 64, 95, 44, 50, 77, 64, 35, 79, 52, 45, 54, 70, 83, 62, 64, 72, 92, 84, 76, 63, 43, 54, 38, 73, 68, 52, 54.
Prepare a frequency distribution table with class size of 10 marks.
Solution :

Question 2.
Below are the marks obtained by 30 students of a class in Maths test out of 100. Make a frequency distribution table for this data with class interval of size 10 and draw a histogram to represent the data. 55, 61, 46, 100, 75, 90, 77, 60, 48, 58, 64, 59, 60, 78, 55, 88, 60, 37, 58, 84, 62, 44, 52, 50, 56, 95, 67, 70, 39, 68.
Solution :
Marks obtained by 30 students are 55, 61, 46, 100, 75, 90, 77, 60, 48, 58, 64, 59, 60, 78, 55, 88, 60, 37, 58, 84, 62, 44, 52, 50, 56, 95, 67, 70, 39, 68.

Question 3.
Find the mean of the factors of 24.
Solution :
Various factors of 24 = 1, 2, 3, 4, 6, 8, 12 and 24.
Mean,
\(\bar{x}\) = Sum of all observations / Total number of observations
= \(\frac{1+2+3+4+6+8+12+24}{8}\)
= \(\frac{60}{8}=\frac{15}{2}\) = 7.5

Question 4.
Find the range of the given data: 25.7, 16.3, 2.8, 21.7, 24.3, 22.7 and 24.9
Solution :
Range of the data = Highest value – Lowest value = 25.7 – 2.8 = 22.9

Multiple Choice Questions

Question 1.
The median of following series 520, 20, 340, 190, 35, 800, 1210, 50, 80 is
(a) 1210
(b) 520
(c) 190
(d) 35
Solution :
(c) 190

Question 2.
If the arithmetic mean of 5, 7, 9, x is 9 then the value of x is
(a) 11
(b) 15
(c) 18
(d) 16
Solution :
(b) 15

Question 3.
The mode of the distribution 3, 5, 7, 4, 2, 1, 4, 3, 4 is
(a) 7
(b) 4
(c) 3
(d) 1
Solution :
(b) 4

Question 4.
If the mean and median of a set of numbers are 8.9 and 9 respectively, then the mode will be
(a) 7.2
(b) 8.2
(c) 9.2
(d) 10.2
Solution :
(c) 9.2

Question 5.
A student got marks in 5 subjects in a monthly test is given below: 2, 3, 4, 5, 6. In these obtained marks, 4 is the
(a) Mean and median
(b) Median but no mean
(c) Mean but no median
(d) Mode
Solution :
(a) Mean and median

Question 6.
Find the mode from the following table:

Marks obtained	3	1	23	33	43
Frequency (f)	7	11	15	8	3

(a) 13
(b) 43
(c) 33
(d) 23
Solution :
(d) 23

Question 7.
If the class intervals in a frequency distribution are (72 – 73.9), (74 – 75.9), (76 – 77.9), (78 – 79.9) etc., the mid-point of the class (74 – 75.9) is
(a) 74.50
(b) 74.90
(c) 74.95
(d) 75.00
Solution :
(c) 74.95

Question 8.
Which one of the following is not correct –
(a) Statistics is liable to be misused.
(b) The data collected by the investigator to be used by himself are called primary data.
(c) Statistical laws are exact.
(d) Statistics do not take into account of individual cases.
Solution :
(c) Statistical laws are exact.

Question 9.
If the first five elements of a sequence are replaced by (x_i + 5), where i = 1, 2, 3, … 5 and the next five elements are replaced by (x_i – 5), where, i = 6; ….. 10 then the mean will change by
(a) 25
(b) 10
(c) 5
(d) 0
Solution :
(d) 0

Question 10.
The following numbers are given: 61, 62, 63, 61, 63, 64, 64, 60, 65, 63, 64, 65, 66, 64. The difference between their median and mean is
(a) 0.4
(b) 0.3
(c) 0.2
(d) 0.1
Solution :
(b) 0.3

Question 11.
The value of \(\sum_{i=i}^n\) (x_i – \(\bar{x}\)) where \(\bar{x}\) is the arithmetic mean of x_i is
(a) 1
(b) n x
(c) 0
(d) None of these
Solution :
(c) 0

Question 12.
The average of 15 numbers is 18. The average of first 8 is 19 and that of last 8 is 17, then the 8th number is
(a) 15
(b) 16
(c) 18
(d) 20
Solution :
(c) 18

Question 13.
In an examination, 10 students scored the following marks in Mathematics: 35, 19, 28, 32, 63, 02, 47, 31, 13, 98. Its range is
(a) 96
(b) 02
(c) 98
(d) 50
Direction: questions 14 is based on the histogram given in the adjacent figure.

Solution :
(a) 96

Question 14.
The percentage of students in science faculty in 1990-91 is:
(a) 26.9 %
(b) 27.8 %
(c) 14.81 %
(d) 30.2 %
Solution :
(c) 14.81 %

Question 15.
For the scores 8, 6, 10, 12, 1, 5, 6 and 6, the arithmetic mean is
(a) 6.85
(b) 6.75
(c) 6.95
(d) 7
Direction: Each question from 16 to 18 is based on the histogram given in the adjacent figure.

Solution :
(b) 6.75

Question 16.
What is the number of workers earning ₹ 300 to 350?
(a) 50
(b) 40
(c) 45
(d) 130
Solution :
(a) 50

Question 17.
In which class interval of wages there is the least number of workers?
(a) 400 – 450
(b) 350 – 400
(c) 250 – 300
(d) 200 – 250
Solution :
(d) 200 – 250

Question 18.
What is the upper limit of the class interval 200-250?
(a) 200
(b) 250
(c) 225
(d) None of these
Solution :
(b) 250

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 13 Surface Areas and Volumes Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 13 Surface Areas and Volumes

Question 1.
Three equal cubes are placed adjacently in a row. Find the ratio of the total surface area of the new cuboid to that of the sum of the surface areas of three cubes.
Solution :
Let the side of each of the three equal cubes be a cm.
Then, surface area of one cube = 6a² cm²
∴ Sum of the surface areas of three cubes = 3 × 6a² = 18 cm²
For new cuboid
length (l) = 3a cm
breadth (b) = a cm
height (h) = a cm
∴ Total surface area of the new cuboid = 2(l × b + b × h + h × l)
= 2[3a × a + a × a + a × 3a]
= 2[3a² + a² + 3a²] = 14a² cm²
∴ Required ratio
= Total surface area of the new cuboid / Sum of the surface areas of three cubes
= \(=\frac{14 \mathrm{a}^2}{18 \mathrm{a}^2}\) = \(\frac {7}{9}\)
= 7 : 9

Question 2.
A classroom is 7 m long, 6.5 m wide and 4 m high. It has one door 3 m × 1.4 m and three windows each measuring 2 m × 1 m. The interior walls are to be colour-washed. The contractor charges ₹ 15 per sq. m. Find the cost of colour washing.
Solution :
l = 7 m, b = 6.5 m and h = 4 m
∴ Area of the walls of the room including door and windows = 2(l + b)h
= 2(7 + 6.5) 4 = 108 m²
Area of door = 3 × 1.4 = 4.2 m
Area of one window = 2 × 1 = 2 m²
∴ Area of 3 windows = 3 × 2 = 6 m²
∴ Area of the walls of the room to be colour washed = 108 – (4.2 + 6)
= 108 – 10.2 = 97.8 m
∴ Cost of colour washing at the rate of ₹ 15 per square metre = ₹ 97.8 × 15 = ₹ 1467

Question 3.
A cylindrical vessel, without lid, has to be tin coated including both of its sides. If the radius of its base is \(\frac {1}{2}\) m and its height is 1.4 m, calculate the cost of tincoating at the rate of ₹ 50 per 1000 cm² (Use π = 3.14)
Solution :
Radius of the base (r) = \(\frac {1}{2}\)m
= \(\frac {1}{2}\) × 100 cm = 50 cm
Height (h) = 1.4 m = 1.4 × 100 cm
= 140 cm.
Surface area to be tin-coated
= 2 (2πh + πr²)
= 2[2 × 3.14 × 50 × 140 + 3.14 × (50)²]
= 2 [43960 + 7850]
= 2(51810)
= 103620 cm²
∴ Cost of tin-coating at the rate of ₹ 50 per 1000 cm²
= \(\frac {50}{1000}\) × 103620 = ₹ 5181.

Question 4.
The diameter of a roller 120 cm long is 84 cm. If its takes 500 complete revolutions to level a playground, determine the cost of levelling it at the rate of ₹ 25 per square metre. (Use π = \(\frac {22}{7}\))
Solution :
diameter of roller = 84 cm
∴ r = \(\frac {84}{2}\) cm = 42 cm
h = 120 cm
Area of the playground levelled in one complete revolution = 2πrh
= 2 × \(\frac {22}{7}\) × 42 × 120 = 31680 cm²
∴ Area of the playground
= 31680 × 500cm² = \(\frac{31680 \times 500}{100 \times 100}\)m²
= 1584 m²
∴ Cost of levelinga at the rate of ₹ 25 per square metre = ₹ 1584 × 25 = ₹ 39600.

Question 5.
How many metres of cloth of 1.1 m width will be required to make a conicaltent whose vertical height is 12 m and base radius is 16 m? Find also the cost of the cloth used at the rate of ₹ 14 per metre.
Solution :
h = 12 m, r = 16 m
∴ l = \(\sqrt{\mathrm{r}^2+\mathrm{h}^2}\)
= \(\sqrt{(16)^2+(12)^2}=\sqrt{256+144}\)
= \(\sqrt{400}\) = 20 m
∴ Curved surface area = πrl
= \(\frac {22}{7}\) × 16 × 20 = \(\frac {7040}{7}\)m²
Width of cloth = 1.1 m
∴ Length of cloth
= \(\frac{7040 / 7}{1.1}=\frac{70400}{77}=\frac{6400}{7}\) m
∴ Cost of the cloth used at the rate of ₹ 14 per metre
= ₹ \(\frac {6400}{7}\) × 14 = ₹ 12800

Question 6.
The surface area of a sphere of radius 5 cm is five times the area of the curved surface of cone of radius 4 cm. Find the height of the cone.
Solution :
Surface area of cone of radius 4 cm = π(4)lcm² where, l cm is the slant height of the cone.
Surface area of sphere of radius 5 cm = π(5)²
According to the question,
4π (5)² = 5[π(4)l]
⇒ l = 5 cm
⇒ \(\sqrt{\mathrm{r}^2+\mathrm{h}^2}\) = 5
⇒ r² + h² = 25
⇒ (4)² + h² = 25
⇒ 16 + h² = 25
⇒ h² = 9
⇒ h = 3
Hence, the height of the cone is 3 cm.

Question 7.
The dimensions of a cinema hall are 100 m, 50 m and 18 m. How many persons can sit in the hall, if each required 150 m³ of air?
Solution :
l = 100 m, b = 50 m, h = 18 m
∴ Volume of the cinema hall = lbh
= 100 × 50 × 18 = 90000 m³
Volume occupied by 1 person = 150 m³
∴ Number of persons who can sit in the hall
= Volume of the hall / Volume occupied by 1 person
= \(\frac {90000}{150}\) = 600
Hence, 600 persons can sit in the hall.

Question 8.
The outer measurements of a closed wooden box are 42 cm, 30 cm and 27 cm. If the box is made of 1 cm thick wood, determine the capacity of the box.
Solution :
Outer dimensions :
l = 42 cm, b = 30 cm, h = 27 cm
Thickness of wood = 1 cm
Inner dimensions :
l = 42 – (1 + 1) = 40 cm
b = 30 – (1 + 1) = 28 cm
h = 27 – (1 + 1) = 25 cm
∴ Capacity of the box = l × b × h = 40 × 28 × 25 = 28000 cm³.

Question 9.
If v is the volume of a cuboid of dimensions a, b and c and s is its surface area, then prove that:
\(\frac{1}{v}=\frac{2}{s}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Solution :
L.H.S. = \(\frac {1}{v}\) = \(\frac {1}{abc}\)
R.H.S. = \(\frac{2}{s}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
= \(\frac{2}{2(a b+b c+c a)}\) (\(\frac{b c+c a+a b}{a b c}\))
= \(\frac {1}{abc}\) ……………(ii)
From (i) and (ii), we have,
\(\frac{1}{v}=\frac{2}{s}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)

Question 10.
The ratio of the volumes of the two cones is 4 : 5 and the ratio of the radii of their bases is 2 : 3. Find the ratio of their vertical heights.
Solution :
Let the radii of bases, vertically heights and volumes of the two cones be r₁, h₁, v₁ and r₂, y₂, v₂ respectively.
According to the question,

Hence the ratio of their vertical heights is 9 : 5.

Question 11.
If h, c and v be the height, curved surface and volume of a cone, show that
3πvh³ – c²h² + 9v² = 0.
Solution :
Let the radius of the base and slant height of the cone be r and l respectively. Then;
C = curved surface area = πrl
= πr\(\sqrt{\mathrm{r}^2+\mathrm{h}^2}\) ………..(i)
v = volume = \(\frac {1}{3}\)πr²h ………..(ii)
∴ 3πvh³ – c²h² + 9v²
= 3πh³(\(\frac {1}{3}\)πr²h) – π²r²(r² + h²)h² + 9(\(\frac {1}{3}\)πr²h)²
[Using (i) and (ii)]
= π²r²h⁴ – π²r⁴h⁴ – π²r²h⁴ – π²r²h²
= 0.
Hence Proved.

Question 12.
How many balls, each of radius 1 cm, can be made from a solid sphere of lead of radius 8 cm?
Solution :
Volume of the spherical ball of radius 8 cm
= \(\frac {4}{3}\)π × 8³cm³
Also, volume of each smaller spherical ball of radius 1 cm
= \(\frac {4}{3}\)π × 1³cm³
Let n be the number of smaller balls that can be made. Then, the volume of the larger ball is equal to the sum of all the volumes of n smaller balls.
Hence, \(\frac {4}{3}\)π × n = \(\frac {4}{3}\)π × 8³
⇒ n = 8³ = 512
Hence, the required number of balls = 512.

Question 13.
By melting a solid cylindrical metal, a few conical materials are to be made. If three times the radius of the cone is equal to twice the radius of the cylinder and the ratio of the height of the cylinder and the height of the cone is 4 : 3, find the number of cones which can be made.
Solution :
Let R be the radius and H be the height of the cylinder and let r and h be the radius and height of the cone respectively. Then,
3r = 2R
And, H : h = 4 : 3 …………..(i)
\(\frac{\mathrm{H}}{\mathrm{h}}=\frac{4}{3}\)
⇒ 3H = 4h …………..(ii)
Let n be the required number of cones which can be made from the materials of the cylinder. Then, the volume of the cylinder will be equal to the sum of the volumes of n cones. Hence, we have
πR²H = \(\frac {n}{3}\)πr²h
3R²H = nr²h
n = \(\frac{3 R^2 H}{r^2 h}=\frac{3 \times \frac{9 r^2}{4} \times \frac{4 h}{3}}{r^2 h}\) = 9
[From (i) and (ii), R = \(\frac {3r}{2}\) and H = \(\frac {4h}{3}\)]
Hence, the required number of cones is 9.

Question 14.
Water flows at the rate of 10 m per minute through a cylindrical pipe having its diameter as 5 mm. How much time will it take to fill a conical vessel whose diameter of the base is 40 cm and depth 24 cm?
Solution :
Diameter of the pipe = 5 mm
= \(\frac {5}{10}\)cm = \(\frac {1}{2}\)cm
∴ Radius of the pipe = \(\frac{1}{2} \times \frac{1}{2}\) cm
= \(\frac {1}{4}\)cm.
In 1 minute, the length of the water column in the cylindrical pipe = 10 m = 1000 cm.
∴ Volume of water that flows out of the pipe in 1 minute
= π × \(\frac {1}{4}\) × \(\frac {1}{4}\) × 1000 cm³
Also, volume of the cone
= \(\frac {1}{3}\) × π × 20 × 20 × 24 cm³.
Hence, the time needed to fill up this conical vessel
= \(\frac{\frac{1}{3} \pi \times 20 \times 20 \times 24}{\pi \times \frac{1}{4} \times \frac{1}{4} \times 1000}\) minutes
= (\(\frac{20 \times 20 \times 24}{3} \times \frac{4 \times 4}{1000}\))minutes
= \(\frac {256}{5}\) minutes
= 51.2 minutes.
Hence, the required time is 51.2 minutes.

Multiple Choice Questions

Question 1.
The height of a conical tent at the centre is 5 m. The distance of any point on its circular base from the top of the tent is 13 m. The area of the slant surface is:
(a) 144 π sq. m
(b) 130 π sq.m
(c) 156 π sq.m
(d) 169 π sq.m
Solution :
(c) 156 π sq.m

Question 2.
A rectangular sheet of paper 22 cm long and 12 cm broad can be curved to form the lateral surface of a right circular cylinder in two ways. Taking π = \(\frac {22}{7}\), the difference between the volumes of the two cylinders thus formed is :
(a) 200 cm³
(b) 210 cm³
(c) 250 cm³
(d) 252 cm³
Solution :
(b) 210 cm³

Question 3.
The percentage increase in the surface area of a cube when each side is increased two times the original length
(a) 225
(b) 200
(c) 175
(d) 300
Solution :
(d) 300

Question 4.
A cord in the form of a square enclose the area ‘S’ cm. If the same cord is bent into the form of a circle, then the area of the circle is
(a) \(\frac{\pi \mathrm{S}^2}{4}\)
(b) 4πS²
(c) \(\frac{4 \mathrm{~S}^2}{\pi}\)
(d) \(\frac {4S}{π}\)
Solution :
(c) \(\frac{4 \mathrm{~S}^2}{\pi}\)

Question 5.
If ‘l’, ‘B’ and ‘h’ of a cuboids are increased, decreased and increased by 1%, 3% and 2% respectively, then the volume of the cuboid
(a) increases
(b) decreases
(c) increases or decreases depending on original dimensions
(d) can’t be calculated with given data
Solution :
(b) decreases

Question 6.
The radius and height of a cone are each increased by 20%, then the volume of the cone is increased by (a) 20%
(b) 40%
(c) 60%
(d) 72.8%
Solution :
(d) 72.8%

Question 7.
There is a cylinder circumscribing the hemisphere such that their bases are common. The ratio of their volumes is
(a) 1 : 3
(b) 1 : 2
(c) 2 : 3
(d) 3 : 4
Solution :
(d) 3 : 4

Question 8.
Consider a hollow cylinder of inner radius r and thickness of wall t and length l. The volume of the above cylinder is given by
(a) 2πl(r² – l²)
(b) 2πrlt(\(\frac {t}{2r}\) + l)
(c) 2πl(r² + l²)
(d) 2πrl(r + l)
Solution :
(b) 2πrlt(\(\frac {t}{2r}\) + l)

Question 9.
A cone and a cylinder have the same base area. They also have the same curved surface area. If the height of the cylinder is 3 m, then the slant height of the cone (in m) is
(a) 3 m
(b) 4 m
(c) 6 m
(d) 7 m
Solution :
(c) 6 m

Question 10.
A sphere of radius 3 cm is dropped into a cylindrical vessel of radius 4 cm. If the sphere is submerged completely, then the height (in cm) to which the water rises, is
(a) 2.35 cm
(b) 2.30 cm
(c) 2.25 cm
(d) 2.15 cm
Solution :
(c) 2.25 cm

Students should go through these JAC Class 9 Maths Notes Chapter 9 Areas of Parallelograms and Triangles will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 9 Maths Notes Chapter 9 Areas of Parallelograms and Triangles

Polygonal Region

Polygon region can be expressed as the union of a finite number of triangular regions in a plane such that if two of these intersect, their intersection is either a point or a line segment. It is the shaded portion including its sides as shown in the figure.

Parallelogram

(a) Base and Altitude of a Parallelogram:
→ Base: Any side of parallelogram can be called its base.
→ Altitude: The perpendicular to the base from the opposite side is called the altitude of the parallelogram corresponding to the given base.
In the given Figure
→ DL is the altitude of ||^gm ABCD corresponding to the base AB.
→ DM is the altitude of ||^gm ABCD, corresponding to the base BC.

Theorem 1.
A diagonal of parallelogram divides it into two triangles of equal area.

Proof:
Given: A parallelogram ABCD whose one of the diagonals is BD.
To prove: ar(ΔABD) = ar(ΔCDB).
Proof: In ΔABD and ΔCDB;
AB = DC [Opp sides of a ||^gm]
AD = BC [Opp. sides of a ||^gm]
BD = BD [Common side]
∴ ΔΑΒD ≅ ΔCDB [By SSS]
ar(ΔABD) = ar (ΔCDB) [Areas of two congruent triangles are equal]
Hence, proved.

Theorem 2.
Parallelograms on the same base or equal base and between the same parallels are equal in area.

Proof:
Given: Two Parallelograms ABCD and ABEF are on the same base AB and between the same parallels AB and FC.
To Prove: ar(||^gm ABCD) = ar(||^gm ABEF)
Proof: In ΔADF and ΔBCE, we have
AD = BC [Opposite sides of a ||^gm]
and AF = BE [Opposite sides of a ||^gm]
AD || BC (Opposite sides of a parallelogram)
⇒ ∠ADF = ∠BCE (Alternate interior angles)
∴ ΔADF ≅ ΔBCE [By AAS]
∴ ar(ΔADF) = ar(ΔBCE) …..(i)
[Congruent triangles have equal area]
∴ ar (||^gm ABCD) = ar(ABED) + ar(ΔBCE)
= ar (ABED) + ar(ΔADF) [Using (1)]
= ar(||^gm ABEF).
Hence, ar(||^gm ABCD) = ar(||^gm ABEF).
Hence, proved.

Theorem 3.
The area of parallelogram is the product of its base and the corresponding altitude.

Proof:
Given: A ||^gm ABCD in which AB is the base and AL is the corresponding height.
To prove: Area (||^gm ABCD) = AB × AL.
Construction: Draw BM ⊥ DC so that rectangle ABML is formed.
Proof: ||^gm ABCD and rectangle ABML are on the same base AB and between the same parallel lines AB and LC.
∴ ar(||^gm ABCD) = ar(rectangle ABML)
= AB × AL
∴ area of a ||^gm = base × height.
Hence, proved.

Area Of A Triangle
Theorem 4.
Two triangles on the same base (or equal bases) and between the same parallels are equal in area.

Proof:
Given: Two triangles ABC and PCB on the same base BC and between the same parallel lines BC and AP.
To prove: ar(ΔABC) = ar(ΔPBC)
Construction: Through B, draw BD || CA intersecting PA produced in D and through C, draw CQ || BP, intersecting line AP produced in Q.
Proof: We have, BD || CA (By construction) And, BC || DA [Given]
∴ Quad. BCAD is a parallelogram.
Similarly, Quad. BCQP is a parallelogram.
Now, parallelogram BOQP and BCAD are on the same base BC, and between the same parallels.
∴ ar (||^gm BCQP) = ar (||^gm BCAD)….(i)
We know that the diagonals of a parallelogram divides it into two triangles of equal area.
∴ ar(ΔPBC) = \(\frac{1}{2}\)(||^gm BCQP) …..(ii)
And ar (ΔABC) = \(\frac{1}{2}\)(||^gm BCAD)….(iii)
Now, ar (||^gm BCQP) = ar(||^gm BCAD) [From (i)]
\(\frac{1}{2}\)ar(||^gm BCAD) = \(\frac{1}{2}\)ar(||^gm BCQP)
Hence, \(\frac{1}{2}\)ar(ABC) = ar(APBC) (Using (ii) and (iii) Hence, proved.

Theorem 5.
The area of a trapezium is half the product of its height and the sum of the parallel sides.

Proof:
Given: Trapezium ABCD in which AB || DC, AL ⊥ DC, CN ⊥ AB and AL = CN = h (say). AB = a, DC = b.
To prove: ar(trap. ABCD) = \(\frac{1}{2}\)h × (a + b).
Construction: Join AC.
Proof: AC is a diagonal of quad. ABCD.
∴ ar(trap. ABCD) = ar(ΔABC) + ar(ΔACD)
= \(\frac{1}{2}\)h × a+\(\frac{1}{2}\)h × b= \(\frac{1}{2}\)h(a + b).
Hence, proved.

Theorem 6.
Triangles having equal areas and having one side of the triangle equal to corresponding side of the other, have their corresponding altitudes equal.

Proof:
Given: Two triangles ABC and PQR such that
(i) ar(ΔABC) = ar(ΔPQR) and
(ii) AB = PQ.
CN and RT and the altitudes corresponding to AB and PQ respectively of the two triangles.
To prove: CN = RT.
Proof: In ΔABC, CN is the altitude corresponding to the side AB
ar(ΔABC) = \(\frac{1}{2}\)AB × CN ……(i)
Similarly, ar(ΔPQR) = \(\frac{1}{2}\)PQ × RT ……(ii)
Since, ar(ΔABC) = ar(ΔPQR) [Given]
∴ \(\frac{1}{2}\)AB × CN = PQ × RT
Also, AB = PQ [Given]
∴ CN = RT Hence, proved.

Jharkhand Board JAC Class 9 Sanskrit Solutions व्याकरणम् उच्चारणस्थानानि Questions and Answers, Notes Pdf.

JAC Board Class 9th Sanskrit व्याकरणम् उच्चारणस्थानानि

सभी वर्गों का उच्चारण मुख से होता है, जिसमें-कण्ठ, जिह्वा, तालु, मूर्धा, दन्त, ओष्ठ एवं नासिका का योगदान होता है। इन उच्चारण-स्थानों से पूर्व ‘वर्ण’ के विषय में आवश्यक ज्ञान अपेक्षित है।

वर्ण – वर्ण उस मूल ध्वनि को कहते हैं, जिसके टुकड़े न हो सकें। जैसे – क्, ख्, ग् आदि। इनके टुकड़े नहीं किये जा सकते। इन्हें अक्षर भी कहते हैं।
वर्ण भेद – संस्कृत में वर्ण दो प्रकार के माने गये हैं। (क) स्वर वर्ण, इन्हें अच् भी कहते हैं। (ख) व्यञ्जन वर्ण, इन्हें हल भी कहा जाता है।
स्वर वर्ण-जिन वर्णों का उच्चारण करने के लिये अन्य किसी वर्ण की सहायता नहीं लेनी पड़ती, उन्हें स्वर वर्ण कहते हैं। स्वर 13 होते हैं। अ, आ, इ, ई, उ, ऊ, ऋ, ऋ, लु, ए, ऐ, ओ, औ।
स्वरों का वर्गीकरण उच्चारण काल अथवा मात्रा के आधार पर स्वर तीन प्रकार के माने गये हैं –
1. ह्रस्व स्वर
2. दीर्घ स्वर
3. प्लुत स्वर।

1. ह्रस्व स्वर-जिन स्वरों के उच्चारण में केवल एक मात्रा का समय लगे अर्थात कम से कम समय लगे, उन्हें ह्रस्व , स्वर कहते हैं। जैसे-अ, इ, उ, ऋ, ल। इनकी संख्या 5 है। इनमें कोई अन्य स्वर या वर्ण मिश्रित नहीं होता, इन्हीं को मूल स्वर भी कहते हैं।

2. दीर्घ स्वर – जिन स्वरों के उच्चारण काल में ह्रस्व स्वरों की अपेक्षा दोगुना समय लगे अर्थात दो मात्राओं का समय लगे, वे दीर्घ स्वर कहलाते हैं। जैसे-आ, ई, ऊ, ऋ, ए, ओ, ऐ, औ। इनकी संख्या 8 है।

3. प्लुत स्वर – जिन स्वरों के उच्चारण में दीर्घ स्वरों से भी अधिक समय लगता है, वे प्लुत स्वर कहलाते हैं। इनमें तीन मात्राओं का उच्चारण काल होता है। इनके उच्चारण काल में दो मात्राओं से अधिक समय लगता है। प्लुत का ज्ञान कराने के लिए ३ अंक स्वर के आगे लगाते हैं। इसका प्रयोग अधिकतर वैदिक संस्कृत में होता है। जैसे – अ ३, इ ३, उ ३, ऋ ३, ल ३, ए ३, ओ ३, ऐ ३, औ ३।

(ख) व्यञ्जन – व्यञ्जन उन्हें कहते हैं, जो बिना स्वर की सहायता के उच्चारित नहीं किये जाते हैं। व्यञ्जन का उच्चारण काल अर्ध मात्रा काल है। जिस व्यञ्जन में स्वर का योग नहीं होता उसमें हलन्त का चिह्न लगाते हैं।
क् ख् ग् घ् ड्
च छ् ज् झ् ञ्
ट् ठ् ड् द् ण्
त् थ् द् ध् न्
प् फ् ब् भ् म्
य र ल व्
श् ष् स् ह
ऊपर लिखे गये ये सभी व्यञ्जन स्वर रहित हैं। इनके स्वर रहित रूप को समझने की दृष्टि से इनमें हल का चिह्न लगाया गया है। जब किसी व्यञ्जन का किसी स्वर के साथ मेल करते हैं, तब हल् का चिह्न हटा देते हैं। जैसे : क् + अ = क।
व्यञ्जन के भेद – उच्चारण की भिन्नता के आधार पर व्यञ्जनों को निम्न तीन भागों में विभाजित किया गया है –

1. स्पर्श
2. अन्तःस्थ
3. ऊष्म।

1. स्पर्श – ‘कादयो मावसाना: स्पर्शाः’ अर्थात जिन व्यञ्जनों का उच्चारण करने में जिह्वा मुख के किसी भाग को स्पर्श करती है और वायु कुछ क्षण के लिए रुककर झटके से निकलती है, वे स्पर्श संज्ञक व्यञ्जन कहलाते हैं। क् से म् पर्यन्त व्यञ्जन स्पर्श संज्ञक हैं। इनकी संख्या 25 है, जो निम्न पाँच वर्गों में विभक्त हैं –

1. क वर्ग क् ख् ग् घ् डू.
2. च वर्ग च् छ् ज् झ् ञ्
3. ट वर्ग ट् ठ् ड् द. ण
4. त वर्ग त् थ द ध न
5. प वर्ग प् फ् ब् भ् म्

2. अन्तःस्थ – जिन व्यञ्जनों का उच्चारण वायु को कुछ रोककर अल्प शक्ति के साथ किया जाता है, वे अन्तःस्थ व्यञ्जन कहलाते हैं। ‘यणोऽन्तःस्थाः ‘ अर्थात् यण (य, व, र, ल) अन्त:स्थ व्यञ्जन हैं। इनकी संख्या चार है।

3. ऊष्म – जिन व्यञ्जनों का उच्चारण वायु को धीरे-धीरे रोककर रगड़ के साथ निकालकर किया जाता है, वे ऊष्म व्यञ्जन कहे जाते हैं। ‘शल ऊष्माणः’ अर्थात् शल्-श, ष, स्, ह ऊष्म संज्ञक व्यञ्जन हैं। इनकी संख्या भी चार है।
इनके अतिरिक्त तीन व्यञ्जन और हैं, जिन्हें संयुक्त व्यञ्जन कहा जाता है, क्योंकि ये दो-दो व्यञ्जनों के मूल से बनते हैं। जैसे –

1. क् + ष् = क्ष्
2. त् + र् = त्र
3. ज् + ञ् = ज्ञ

अयोगवाह-वर्ण

1. अनुस्वार – स्वर के ऊपर जो बिन्दु (.) लगाया जाता है, उसे अनुस्वार कहते हैं। स्वर के बाद न् अथवा म् के स्थान पर अनुस्वार का प्रयोग किया जाता है। यथा –
(i) इयम् गच्छति-इयं गच्छति, (ii) यशान् + सि = यशांसि। इसके अन्य उदाहरण हैं-अंश, अवतंस, हंस, धनूंषि, बृंहितम, सिंह, हिंसक आदि।

2. अनुनासिक – बू, , डू. ण, न; ये पाँच व्यञ्जन अनुनासिक माने जाते हैं। इन्हें अर्द्ध अनुस्वार भी कहा जाता है, जिसे चन्द्रबिन्दु (ँ) के नाम से भी जाना जाता है। यथा-कहाँ, वहाँ, यहाँ, पाँच आदि।

3. विसर्ग स्वरों के आगे आने वाले दो बिन्दुओं (:) को विसर्ग कहते हैं। विसर्ग का उच्चारण आधे ह की तरह किया जाता है। इसका प्रयोग किसी स्वर के बाद किया जाता है। यह र और स् के स्थान पर भी आता है। जैसे – रामः, भानुः इत्यादि।

4. जिह्वामूलीय – (क, ख) इसका प्रयोग क् एवं ख से पहले किया जाता है अर्थात क् एवं ख् से पूर्व अर्द्ध विसर्ग सदृश चिह्न को जिह्वामूलीय कहते हैं। जैसे – सः करोति (क्)। सः खादति (ख)।

5. उपध्मानीय – (पफ) इसका प्रयोग प् एवं फ से पूर्व अर्द्ध विसर्ग के समान किया जाता है। जैसे-कः पचति (प्)। वृक्षः फलति। ( फ्)।

क वर्ग से प वर्ग तक पाँचों वर्गों के प्रथम और द्वितीय अक्षरों (क, ख, च, छ आदि) तथा ऊष्म वर्णों (श, ष, स, ह) को ‘परुष’ व्यञ्जन और शेष वर्गों (ग घ आदि) को ‘कोमल’ व्यञ्जन कहते हैं। व्यञ्जनों के दो प्रकार हैं- अल्पप्राण तथा महाप्राण। पाँचों वर्गों के पहले और तीसरे वर्ग (क, ग, च, ज आदि) ‘अल्पप्राण’ हैं तथा दूसरे और चौथे वर्ण (ख, घ, छ, झ) ‘महाप्राण’ हैं। वर्गों के पञ्चम वर्ण (ङ, ञ, ण, न, म्) अनुनासिक व्यञ्जन कहलाते हैं।

वर्णों के उच्चारण स्थान –

संस्कृत वर्णमाला में पाणिनीय शिक्षा (व्याकरण) के अनुसार 63 वर्ण हैं। उन सभी वर्गों के उच्चारण के लिए आठ स्थान हैं। जो ये हैं – (1) उर, (2) कण्ठ, (3) शिर (मूर्धा), (4) जिह्वामूल, (5) दन्त, (6) नासिका, (7) ओष्ठ और (8) तालु।

उन उच्चारण स्थानों का विभाजन निम्न रूप में किया जाता है –
1. कण्ठ – ‘अकुहविसर्जनीयानां कण्ठः’ अर्थात् अकार (अ, आ), क वर्ग (क, ख, ग, घ, ङ्) और विसर्ग का उच्चारण स्थान कण्ठ होता है। कण्ठ से उच्चारण किये गये वर्ण ‘कण्ठ्य’ कहलाते हैं।)

2. तालु – इचुयशानां तालु’ अर्थात् इ, ई, च वर्ग (च, छ, त्, झ, ञ्), य् और श् का उच्चारण स्थान तालु है। तालु से उच्चारित वर्ण ‘तालव्य’ कहलाते हैं। इन वर्गों का उच्चारण करने में जिह्वा तालु (दाँतों के मूल से थोड़ा ऊपर) का स्पर्श करती है।

3. मूर्धा – ‘ऋटुरषाणां मूर्धा’ अर्थात् ऋ, ऋ, ट वर्ग (ट्, ठ्, ड्, द, ण), र और ष का उच्चारण स्थान मूर्धा है। इस स्थान से उच्चारित वर्ण ‘मूर्धन्य’ कहे जाते हैं। इन वर्गों का उच्चारण जिह्वा मूर्धा (तालु से भी ऊपर गहरे गड्ढेनुमा भाग) का स्पर्श करती है।

4. दन्त – ‘लुतुलसानां दन्ताः ‘अर्थात् लु, त वर्ग (त्, थ, द्, ध्, न्), ल और स् का उच्चारण स्थान दन्त होता है। दन्तर स्थान से उच्चारित वर्ण ‘दन्त्य’ कहलाते हैं। इन वर्गों का उच्चारण करने में जिह्वा दाँतों का स्पर्श करती है।

5. ओष्ठ – ‘उपूपध्मानीयानामोष्ठौ’ अर्थात् उ, ऊ, प वर्ग (प्, फ्; ब्, भ, म्) तथा उपध्मानीय ( प, फ) का उच्चारणस्थान ओष्ठ होते हैं। ये वर्ण ‘ओष्ठ्य’ कहलाते हैं। इन वर्गों का उच्चारण करते समय दोनों ओष्ठ आपस में मिलते हैं।

6. नासिक – (i) ‘जमङ्गनानां नासिका च’ अर्थात् ज, म्, ङ, ण, न् तथा अनुस्वार का उच्चारण स्थान नासिका है। इस स्थान से उच्चारित वर्ण ‘नासिक्य’ कहलाते हैं। इन वर्गों के पूर्वोक्त अपने-अपने वर्ग के अनुसार कण्ठादि उच्चारण स्थान भी होते हैं। जैसे – क वर्ग के ‘ङ्’ का उच्चारण स्थान तालु और नासिका, ट वर्ग के ‘ण’ का मूर्धा और नासिका, त वर्ग के ‘न्’ का दन्त और नासिका तथा प वर्ग के ‘म्’ का ओष्ठ और नासिका होता है।

(ii) नासिकाऽनुस्वारस्यं – अर्थात् अनुस्वार (-) का उच्चारण स्थान नासिका (नाक) होती है।

7. कण्ठतालु – ‘एदैतोः कण्ठतालु’ अर्थात् ए तथा ऐ का उच्चारण स्थान कण्ठतालु होता है। अतः ये वर्ण ‘कण्ठतालव्य’ कहे जाते हैं। अ, इ के संयोग से ए तथा अ, ए के संयोग से ऐ बनता है। अतः ए तथा ऐ के उच्चारण में कण्ठ तथा तालु दोनों का सहयोग लिया जाता है।

8. कण्ठोष्ठ ‘ओदौतोः कण्ठोष्ठम्’ अर्थात् ओ तथा औ का उच्चारण स्थान कण्ठोष्ठ होता है। अ + उ = ओ तथा अ + ओ = औ बनते हैं। अतः इनके उच्चारण में कण्ठ तथा ओष्ठ दोनों का उपयोग किया जाता है। ये वर्ण ‘कण्ठोष्ठ्य’ कहलाते हैं।

9. दन्तोष्ठ ‘वकारस्य दन्तोष्ठम्’ अर्थात् व का उच्चारण स्थान दन्तोष्ठ होता है। इस कारण ‘व”दन्तोष्ठ्य’ कहलाता है। इसका उच्चारण करते समय जिह्वा दाँतों का स्पर्श करती है तथा ओष्ठ भी कुछ मुड़ते हैं। अतः दोनों के सहयोग से वकार का उच्चारण किया जाता है।

10. जिह्वामूल – ‘जिह्वामूलीयस्य जिह्वामूलम्’ अर्थात् जिह्वामूलीय (क-ख) का उच्चारण स्थान जिह्वामूल होता है। उपर्युक्त वर्णोच्चारण स्थानों को नीचे दी गई तालिका के माध्यम से सरलता से जाना जा सकता है।

वर्ण-उच्चारण-स्थान तालिका

प्रत्याहार –

1. अक् अ इ उ ऋ लु।
2. अच् अ इ उ ऋ ल ए ओ ऐ औ।
3. अण् अ इ उ
4. अट् अ इ उ ऋ ल ए ओ ऐ औ ह य व र।
5. अण् अ इ उ ऋ ल ए ओ ए औ ह य् व् र् ल।
6. अम् अ इ उ ऋ ल ए ओ ए औ ह य् व् र् ल् ब् भ् डू. ण न्।
7. अश् अ इ उ ल ए ओ ऐ औ ह य व् र् ल् ज् म् डू ण् न् झ् भ् थ् द् ध् ज् ब् ग् इन्।
8. अल अ इ उ ऋ ल ए ओ ऐ औ ह य् व् र् ल् ब् म् डू. ण् न् झ् भ् थ् द् ध् ज् ब् म् ड् द् ख् फ् छ् त् थ् च् ट् त् क् प् श् ष् स्।
9. इक्इ उ ऋ ल।
10. इच् इ उ ऋ ल ए ओ ऐ औ।
11. इण् इ उ ऋ ल ए ओ ऐ औ ह य व.र ल।
12. उक् उ ऋ ल।
13. एडू. ए ओ।
14. एच ए ओ ऐ औ।
15. ऐच् ऐ और
16. खय् ख् फ् छ् ठ् थ् च् ट् त् क् ।
17. खर् ख् फ् छ् ठ् थ् च् ट् त् क् प् श् ष् स्।
18. ङम् ड्. ण न्।
19. चय् च् ट् त् क्
20. चर् च् ट् त् क् य श् ष् स्।
21. छव च् ट् त्।
22. जश् ज् ब् ग् ड् द्।
23. भय् झ भ घ ढ ध ज् ब् ग् ड् द् ख् फ् छ् ठ् घ् च ट् त् क् ।
24. झर् झ म् घ् ढ् ध् ज् ब् ग् ड् द् ख् फ् घ् त् थ् च् त् ट् क् प् श् ष् स्।
25. झल झ भ् घ् ढ् ध् ज् ब् ग् ड् द् ख् फ् छ् त् थ् च् ट् त् क् प् श् ष् स् ।
26. भश् झ भ् थ् द् ध् ज् ब् ग् ड् द्।
27. भष् झ् भ् थ् द् धु
28. बश् ब् ग् ड् द्
29. मय् म् ड्. ण् न् झ् भ् थ् द् ध् ज् ब् ग् ड् द् ख् फ् छ् त् थ् च् ट् त् क् प्।
30. य य् व् र् ल् ञ् म् इ. ण् न् झ्।
31. यण् य् व् र् ल।
32. यम् य् व् र् ल् ज् म् ड्. ण न्।
33. यय् य् व् र् ल् ब् म् ड्. ण् न् झ् भ् घ् ढ् ध् ज् ब् ग् ड् द् ख् प् छ् ठ् थ् च् ट् त् क्।
34. यर् य् व् र् ल् ज् म् ड्. ण् न् क्ष् घ् द् ध् ज् ब् ग् ड् द् ख् फ् छ् ठ् थ् च् त् क प् श् ष् स्।
35. रल र् ल् ब् म् ड्. ण् न् झ् भ् घ् ढ् ध् ज् व् ग् ड् द् ख् फ् छ् त् थ् च् ट् त् क् प् य् श् ष् स् ह्।
36. वल् व् र् ल् ज् म् ड्. ण् न् झ् भ् घ् ढ् ध् ज् ब् ग् ड् द् ख् फ् छ् त् थ् च् ट् त् क् प् श ष स ह्।
37. वश व् र् ल् ब् भ् ड्. ण न् झ् भ् थ् द् ध् ज् ब् ग् ड् द्।
38. शर् श् ष् स्।
39. शल् श् ष् स् ह्।
40. र र् ल।

प्रयत्न

वर्गों के उच्चारण में जो चेष्टा करनी पड़ती है, उसे प्रयत्न कहते हैं। ये प्रयत्न दो प्रकार के होते हैं।

1. आभ्यान्तर प्रयत्न।
2. बाह्य प्रयत्न।

1. आभ्यान्तर प्रयत्न – मुख के भीतरी अवयवों द्वारा किया गया यल आभ्यान्तर प्रयत्न कहलाता है। यह पाँच प्रकार का होता है –
(i) स्पृष्ट – इसका अर्थ है, उच्चारण के समय जीभ द्वारा मुख के अन्दर विभिन्न उच्चारण स्थानों का किया गया स्पर्श इस प्रयत्न द्वारा सभी 25 स्पर्श व्यञ्जन क् से म् तक उच्चारित होते हैं। पाँचों वर्गों के अक्षरों का स्पृष्ट प्रयत्न होता है।
(ii) ईषत्स्पष्ट अर्थात् थोड़ा स्पर्श। जब जीभ मुख के अन्दर तालु आदि उच्चारण स्थानों का कम स्पर्श करती है, तो इस प्रयत्न को ईषत्स्पृष्ट प्रयत्न कहा जाता है। अन्त:स्थ व्यञ्जन वर्णों (य् र् ल व) का ईशत्स्पृष्ट प्रयत्न होता है।
(iii) विवृत-इसका अर्थ है, उच्चारण के समय कण्ठ का खुलना। जब विभिन्न उच्चारणों में कण्ठ-विवर खुलता है, तो इस प्रयत्न को विवृत प्रयत्न कहा जाता है। सभी स्वर वर्णों का विवृत प्रयत्न होता है।
(iv) ईषद् विवृत-जब वर्गों के उच्चारण काल में कण्ठ पूरी तरह न खुलकर स्वल्प (थोड़ा सा) खुलता है तब ऐसे प्रयत्न को ईषद् विवृत प्रयत्न कहा जाता है। ऊष्म वर्णों (श् ष् स् ह) का ईषद् विवृत प्रयत्न होता है।
(v) संवत-संवृत का अर्थ है-बन्द। ह्रस्व अकार का उच्चारण संवृत-प्रयल है।

2. बाह्य प्रयत्न वर्गों के उच्चारण में जिस प्रकार मुख के अन्दर प्रयत्न अथवा चेष्टाएँ होती हैं, उसी प्रकार कुछ चेष्टाएँ बाहर से भी होती हैं, जिन्हें हम बाह्य प्रयत्न कहते हैं। ये निम्न हैं.
(i) विवार – वर्ण के उच्चारण के समय मुख के खुलने को विवार कहा जाता है। वर्गों के पहले तथा दूसरे वर्ण एवं श् प् स् विवार प्रयत्न द्वारा उच्चारित होते हैं।
(ii) संवार – जब वर्ण के उच्चारण में मुख कुछ संकुचित होता है, तब ऐसे प्रयत्न को संवार प्रयत्न कहा जाता है। इसके अन्तर्गत सभी वर्गों के तीसरे, चौथे तथा पाँचवें वर्ग एवं अन्त:स्थ व्यञ्जन आते हैं।
(ii) श्वास – जिनके उच्चारण में श्वास की गति विशेष रूप से प्रभावित होती है, उन्हें श्वास वर्ग की संज्ञा दी जाती है, इसके अन्तर्गत सभी वर्गों के पहले, दूसरे तथा ऊष्म वर्ण आते हैं।
(iv) नाद वर्णों के उच्चारण में विशेष प्रकार की अव्यक्त ध्वनि को नाद कहते हैं, किसी भी वर्ग के तीसरे, चौथे और पाँचवें वर्ण तथा शल वर्ण (श ष स ह) नाद प्रयत्न द्वारा उच्चारित होते हैं।
(v) घोष – उच्चारण में होने वाले विशेष शब्द को घोष कहा जाता है। वर्गों के तीसरे, चौथे व पाँचवें वर्ण घोष प्रयत्न द्वारा बोले जाते हैं।
(vi) अघोष – जिन वर्गों के उच्चारण में घोष ध्वनि नहीं होती, उन्हें अघोष प्रयत्ल द्वारा उच्चारित किया जाता है। इनमें वर्गों के पहले, दूसरे तथा अन्त:स्थ व्यञ्जन आते हैं।
(vii) अल्पप्राण – जिन वर्णों के उच्चारण में कम मात्रा में वायु मुख के भीतरी भाग से बाहर निकलती है, उन वर्गों को अल्पप्राण वर्ण कहा जाता है। वर्गों के पहले, तीसरे और पाँचवें वर्ण अल्पप्राण कहलाते हैं।
(viii) महाप्राण – जिन वर्णों के उच्चारण में अधिक प्राणवायु का उपयोग होता है, ऐसे वर्णों को महाप्राण वर्ण कहा जाता है। वर्गों के दूसरे और चौथे वर्ण महाप्राण कहलाते हैं।
(ix) उदात्त – तालु आदि से उच्चारण में अधिक प्राणवायु का उपयोग होता है, ऐसे वर्णों को महाप्राण वर्ण कहा जाता है। वर्गों के दूसरे और चौथे वर्ण महाप्राण कहलाते हैं।
(x) अनुदात्त – तालु आदि उच्चारण स्थानों के निचले भाग से उच्चारित स्वर-वर्णों को अनुदात्त प्रयत्न वाला कहा जाता है।
(xi) स्वरित – जब वायु तालु आदि उच्चारण स्थलों के मध्य भाग से निकलती है, तो ऐसे प्रयत्न स्वरित प्रयत्न कहे जाते हैं।
सवर्ण-जिन वर्णों के उच्चारण स्थान तथा प्रयत्न दोनों एक हों उन वर्णों को सवर्ण अथवा समान वर्ण कहते हैं असमान वर्ण जब वणों के उच्चारण स्थान या प्रयत्न भिन्न-भिन्न हों, तो ऐसे वर्गों को असमान वर्ण कहते हैं।

अभ्यास 1

प्रश्न 1.
‘ग्’ वर्णस्य उच्चारणस्थानम् अस्ति। (‘ग्’ वर्ण का उच्चारण स्थान है.)
(अ) तालु
(ब) नासिका
(स) कण्ठः
(द) ओष्ठौ।
उत्तर :
(स) कण्ठः

प्रश्न 2.
‘द्’ वर्णस्य उच्चारणस्थानम् अस्ति – (‘द्’ वर्ण का उच्चारण स्थान है-)
(अ) कण्ठः
(ब) तालुः
(स) दन्तः
(द) मूर्धाः
उत्तर :
(स) दन्तः

प्रश्न 3.
अनुस्वारस्य उच्चारणस्थानं भवति-(अनुस्वार का उच्चारण स्थान होता है-)
(अ) नासिका
(ब) कण्ठः
(स) ओष्ठौः
(द) दन्तः।
उत्तर :
(अ) नासिका

प्रश्न 4.
‘छ’ वर्णस्य उच्चारणस्थानम् अस्ति (छ’ वर्ण का उच्चारण स्थान है-)
(अ) कण्ठः
(ब) तालु
(स) मूर्धा
(द) ओष्ठौ।
उत्तर :
(अ) कण्ठः

प्रश्न 5.
‘ड’ वर्णस्य उच्चारणस्थानम् अस्ति-(‘ड्’ वर्ण का उच्चारण स्थान है )
(अ) मूर्धा
(ब) कण्ठतालु
(स) तालु
(द) ओष्ठौ।
उत्तर :
(अ) मूर्धा

प्रश्न 6.
हकारस्य उच्चारणस्थानं भवति-(हकार का उच्चारण स्थान होता है)
(अ) कण्ठः
(ब) तालु
(स) मूर्धा
(द) ओष्ठौ।
उत्तर :
(अ) कण्ठः

प्रश्न 7.
‘ष’ वर्णस्य उच्चारणस्थानम् अस्ति-(‘ए’ वर्ण का उच्चारण स्थान है-)
(अ) तालु
(ब) मूर्धा
(स) कण्ठः
(द) ओष्ठौ
उत्तर :
(ब) मूर्धा

प्रश्न 8.
‘जश’ प्रत्याहारान्तर्गत परिगणिताः वर्णाः सन्ति-(‘जश्’ प्रत्याहार में परिगणित होने वाले वर्ण हैं-)
(अ) ह् य् व् र् ल्
(ब) क् प् श् ष् स्
(स) ज् ब् ग् ड् द्
(द) झ् भ् घ् द ध्।
उत्तर :
(स) ज् ब् ग् ड् द्

प्रश्न 9.
‘एच’ प्रत्याहारान्र्तगताः वर्णाः सन्ति-(‘एच’ प्रत्याहार में आने वाले वर्ण हैं)
(अ) अ, इ, उ, ऋ, लु
(ब) ए, ओ, ऐ, औ
(स) ए, ओ
(द) ऐ, औ।
उत्तर :
(ब) ए, ओ, ऐ, औ

प्रश्न 10.
‘अक्’ प्रत्याहारन्तर्गता. वर्णाः सन्ति-(‘अक्’ प्रत्याहार में आने वाले वर्ण हैं –
(अ) अ, इ, उ ऋ, ल
(ब) अ, इ उ
(स) इ, उ, ऋ, ल
(द) अ, इ, उ, ऋ, लु, ए, ओ, ए।
उत्तर :
(अ) अ, इ, उ ऋ, ल

अभ्यास 2

प्रश्न 1.
‘शल्’ प्रत्याहारान्तर्गताः वर्णाः सन्ति-(‘शल्’ प्रत्याहार में आने वाले वर्ण हैं )
(अ) श् ष् स्
(ब) श् ष् स् ह्
(स) क् प् श् ष् स् ह
(द) ज् ब् ग् ड् द्।
उत्तर :
(ब) श् ष् स् ह्

प्रश्न 2.
‘यण’ प्रत्याहारान्तर्गताः वर्णाः सन्ति-(‘यण’ प्रत्याहार में आने वाले वर्ण हैं)
(अ) ह य् व् र् ल्
(ब) श् ष स ह
(स) य् व् र् ल्
(द) ज् द् ग् ड् द्।
उत्तर :
(स) य् व् र् ल्

प्रश्न 3.
‘इक्’ प्रत्याहारान्तर्गताः वर्णाः सन्ति-(‘इक्’ प्रत्याहार में आने वाले वर्ण हैं)
(अ) अ, इ, उ,
(ब) अ, इ, उ, ऋ, लु
(स) ए, ओ, ऐ, औ
(द) इ, उ, ऋ, ल।
उत्तर :
(द) इ, उ, ऋ, ल।

प्रश्न 4.
‘हल’ प्रत्याहारास्य वर्णाः कथ्यन्ते-(‘हल्’ प्रत्याहार के वर्गों को कहते हैं-)
(अ) स्वर
(ब) स्पर्श
(स) व्यञ्जन
(द) ऊष्म।
उत्तर :
(स) व्यञ्जन

प्रश्न 5.
स्पर्शवर्णानां आभ्यान्तरप्रयत्नं भवति-(स्पर्श वर्णों का आभ्यान्तर प्रयत्न होता है-)
(अ) विवृत
(ब) संवृत
(स) स्पृष्ट
(द) ईषत् स्पृष्ट।
उत्तर :
(स) स्पृष्ट

प्रश्न 6.
महाप्राणप्रयत्नः केषां वर्णानां भवति-(‘महाप्राण’ प्रयत्न वाले कौन-से वर्ण हैं-)
(अ) शल्
(ब) यण
(स) अच्
(द) जश्।
उत्तर :
(अ) शल्

प्रश्न 7.
‘घोष’ वर्णाः सन्ति – (घोष’ वर्ण हैं)
(अ) ग, घ, ड.
(ब) त, क, न
(स) य, र, त
(द) न, ड., क।
उत्तर :
(अ) ग, घ, ड.

प्रश्न 8.
‘ध्’ वर्णस्य उच्चारणस्थानम् अस्ति। (‘ध्’ वर्ण का उच्चारण स्थान है-)
(अ) ओष्ठौ
(ब) दन्ताः
(स) तालु
(द) मूर्धा।
उत्तर :
(ब) दन्ताः

प्रश्न 9.
‘थ्’ वर्णस्य उच्चारणस्थानम् अस्ति-(‘थ्’ वर्ण का उच्चारण स्थान है-)
(अ) मर्धा
(ब) ओष्ठौ
(स) कण्ठः
(द) दन्ताः
उत्तर :
(द) दन्ताः

प्रश्न 10.
‘ओ’ वर्णस्य’औ’वर्णस्य च उच्चारणस्थानम अस्ति-(ओ तथा औ वर्णों का उच्चारण स्थान है )
(अ) कण्ठःतालु
(ब) कण्ठनासिका
(स) कण्ठजिह्वा
(द) कण्ठोष्ठम्।
उत्तर :
(ब) कण्ठनासिका

अभ्यास 3

प्रश्न 1.
‘ब’ वर्णस्य उच्चारणस्थानम् अस्ति (‘ब’ वर्ण का उच्चारण स्थान है)
(अ) मूर्धा
(ब) दन्ताः
(स) ओष्ठौ
(द) कण्ठः
उत्तर :
(ब) दन्ताः

प्रश्न 2.
‘ओ’ वर्णस्य उच्चारणस्थानम् अस्ति-(‘ओ’ वर्ण का उच्चारण स्थान है)
(अ) कण्ठोष्ठी
(ब) दन्तोष्ठौ
(स) मूर्धा
(द) दन्ताः
उत्तर :
(स) मूर्धा

प्रश्न 3.
ऐकारस्य उच्चारणस्थानम् अस्ति-(‘ऐकार’ का उच्चारण स्थान है-)
(अ) नासिका
(ब) कण्ठतालु
(स) कण्ठोष्ठौ
(द) दन्ताः।
उत्तर :
(अ) नासिका

प्रश्न 4.
ऋकारस्य उच्चारणस्थानम् अस्ति-(‘ऋकार’ का उच्चारण स्थान है)
(अ) मूर्धा
(ब) तालु
(स) कण्ठः
(द) दन्ताः।
उत्तर :
(अ) मूर्धा

प्रश्न 5.
वकारस्य उच्चारणस्थानम् अस्ति – (‘वकार’ का उच्चारण स्थान है-)
(अ) कण्ठोष्ठौ
(ब) दन्तोष्ठी
(स) जिह्वामूल
(द) दन्ताः
उत्तर :
(अ) कण्ठोष्ठौ

प्रश्न 6.
‘न्’ वर्णस्य उच्चारणस्थानम् अस्ति-(‘न्’ वर्ण का उच्चारण स्थान है )
(अ) ओष्ठौ
(ब) दन्ता
(स) नासिका
(द) कण्ठः
उत्तर :
(अ) ओष्ठौ

प्रश्न 7.
‘आ’ वर्णस्य उच्चारणस्थानम् अस्ति-(‘आ’ वर्ण का उच्चारण स्थान है-)
(अ) दन्ताः
(ब) तालु
(स) नासिका
(द) कण्ठः
उत्तर :
(द) कण्ठः

प्रश्न 8.
‘ई’ वर्णस्य उच्चारणस्थानम् अस्ति-(‘ई’ वर्ण का उच्चारण स्थान है-)
(अ) तालु
(ब) मूर्धा
(स) दन्ताः
(द) ओष्ठौ।
उत्तर :
(अ) तालु

प्रश्न 9.
रकारस्य उच्चारणस्थानम् अस्ति – (‘रकार’ का उच्चारण स्थान है-)
(अ) तालु
(ब) मूर्धा
(स) ओष्ठौ
(द) कण्ठः
उत्तर :
(ब) मूर्धा

प्रश्न 10.
लकारस्य उच्चारणस्थानम् अस्ति-(‘लकार’ का उच्चारण स्थान है)
(अ) ओष्ठौ
(ब) दन्ताः
(स) तालु
(द) कण्ठोष्ठौ।
उत्तर :
(ब) दन्ताः

अभ्यास 4

1. तालु कस्य वर्गस्य उच्चारणस्थानं भवति? (तालु किस वर्ग का उच्चारण स्थान होता है?)
2. कण्ठः कस्य वर्गस्य उच्चारणस्थानं भवति? (कण्ठ किस वर्ग का उच्चारण स्थान होता है?)
3. मूर्धा कस्य वर्गस्य उच्चारणस्थानं भवति? (मूर्धा किस वर्ग का उच्चारण स्थान है?)
4. ओष्ठौ कस्य वर्गस्य उच्चारणस्थानं भवति? (ओष्ठ किस वर्ग के उच्चारण स्थान हैं?)
5. दन्ताः कस्य वर्गस्य उच्चारणस्थानं भवति? (दाँत किस वर्ग के उच्चारण स्थान होते हैं?)
6. नासिका केषां वर्णानाम उच्चारणस्थानं भवति? (नासिका किन वर्गों की उच्चारण स्थान होती है?)
7. उच्चारणस्थानानि कति सन्ति? (उच्चारण स्थान कितने हैं ?)
8. वर्णोच्चारणे कस्याः परमसहयोगो भवति? (वर्ण उच्चारण में किसका परम सहयोग होता है?)
9. पवर्गस्य उच्चारणस्थानं किं भवति? (प वर्ग का उच्चारण स्थान क्या है?)
10. दन्तोष्ठम् उच्चारणस्थानं कस्य वर्णस्य अस्ति? (दन्तोष्ठ किस वर्ग का उच्चारण स्थान है?)
उत्तरम् :
1. चवर्गस्य
2. कवर्गस्य
3. टवर्गस्य
4. पवर्गस्य
5. तवर्गस्य
6. ञ, म, ङ, ण, न्
7. अष्टौ
8. जिह्वायाः
9. ओष्ठौ
10. ‘व’ वर्णस्य।

अभ्यास 5

1. प्रयत्नानि कति भवन्ति? (प्रयत्न कितने होते हैं?)
2. आभ्यान्तरप्रयत्नस्य कति भेदाः सन्ति? (आभ्यन्तर प्रयत्न के कितने भेद हैं?)
3. बाह्यप्रयत्नस्य कति भेदाः सन्ति? (बाह्य प्रयत्न के कितने भेद हैं?)
4. स्पर्शवर्णानाम् अन्य नाम किमस्ति? (स्पर्श वर्णों का दूसरा नाम क्या है?)
5. स्पर्शवर्णाः कानि-कानि सन्ति? (स्पर्श वर्ण कौन-कौन से हैं?)
6. महाप्राणाः के भवन्ति? (महाप्राण कौन हैं ?)
7. ऊष्मसंज्ञकाः वर्णा: के सन्ति? (अन्तःस्थ व्यंजन कौन हैं?)
उत्तरम् :
1. माहेश्वरसूत्रस्य
2. द्वे
3. पञ्च
4. एकादशः
5. उदितवर्णाः
6. क् ख् ग् घ् ङ् च् छ त् झ् ञ् ट ठ् ड् द ण् त् थ् द् ध् न् प् फ् ब् भ् म्
7. वर्गस्य द्वितीयचतुर्थवर्णाः
8. श् ष् स् ।

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 5 Introduction to Euclid’s Geometry Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 5 Introduction to Euclid’s Geometry

Multiple Choice Questions

Question 1.
How many lines pass through one point?
(a) 0
(b) 1
(c) 5
(d) Infinite
Solution :
(d) Infinite

Question 2.
How many lines can be drawn to pass through three given points if they are not collinear?
(a) 1
(b) 2
(c) 3
(d) Infinite
Solution :
(d) Infinite

Question 3.
A point is that which has ______ part(s)
(a) Zero
(b) One
(c) Five
(d) two
Solution :
(a) Zero

Question 4.
_____ is a collection of infinite number of points.
(a) point
(b) line
(c) surface
(d) plane
Solution :
(b) line

Students should go through these JAC Class 9 Maths Notes Chapter 15 Probability will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 9 Maths Notes Chapter 15 Probability

Probability:
Theory of probability deals with measurement of uncertainty of the occurrence of some event or incident in terms of percentage or ratio.
→ Sample Space: Set of all possible outcomes.
→ Trial: Trial is an action which results in one of several outcomes.
→ An experiment: An experiment is any kind the of activity such as throwing a die, tossing a coin, drawing a card. The different possibilities which can occur during an experiment. e.g. on throwing a dice, 1 dot, 2 dots, 3 dots, 4 dots, 5 dots, 6 dots can occur.
→ An event: Getting a ‘six’ in a throw of dice, getting a head, in a toss of a coin.
→ A random experiment: is an experiement that can be repeated numerous times under the same conditions.
→ Equally likely outcomes: The outcomes of a sample space are called equally likely if all of them have same chance of occurring.
→ Probability of an event A: Written as P(A) in a random experiment and is defined as –
P(A) = \(\frac{\text { Number of outcomes in favour of A }}{\text { Total number of possible outcomes }}\)

Important Properties:
(i) 0 ≤ P(A) ≤ 1
(ii) P (not happening of A) + P (happening of A) = 1
or, P(\(\bar{A}\)) + P(A) = 1
∴ P(\(\bar{A}\)) = 1 – P(A)
Probability of the happening of A = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{\mathrm{m}}{\mathrm{m}+\mathrm{n}}\)
Probability of not happening of A (failing of A) = \(\frac{\mathrm{n}}{\mathrm{m}+\mathrm{n}}\)
where event A can happen in m ways and fail in n ways. All these ways being equally likely to occur.

Problems of Die:
A die is thrown once. The probability of
→ Getting an even number in the throwing of a die: the total number of outcomes is 6. Let A be the event of getting an even number then there are three even numbers 2, 4, 6.
∴ Number of favourable outcomes = 3.
P(A) = \(\frac{\text { Number of favourable outcomes }}{\text { Total number of possible outcomes }}\)
= \(\frac{3}{6}=\frac{1}{2}\)

→ Getting an odd number: Total no. of outcomes = 6,
favourable outcomes = 3 i.e. {1, 3, 5}
∴ P(A) = \(\frac{3}{6}=\frac{1}{2}\)
→ Getting a natural number P(A) = \(\frac{6}{6}\) = 1
→ Getting a number which is multiple of 2 and 3 = \(\frac{1}{6}\)
→ Getting a number ≥3 i.e. {3, 4, 5, 6},
P(A) = \(\frac{4}{6}\) = \(\frac{2}{3}\)
→ Getting a number 5 or 6, P(A) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
→ Getting a number ≤5 i.e. {1, 2, 3, 4, 5},
P(A) = \(\frac{5}{6}\)

Problems Concerning Drawing a Card:

• A pack of 52 cards
• Face cards (King, Queen, Jack)