JAC Class 9 Maths Important Questions Chapter 12 Heron’s Formula

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 12 Heron’s Formula Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 12 Heron’s Formula

Question 1.
The area of a triangle is 30 cm². Find the base if the altitude exceeds the base by 7 cm.

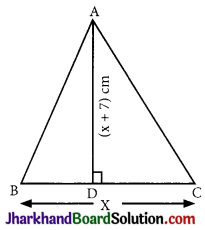
Solution :
Let base BC = x cm
Then altitude = (x + 7) cm
Area of ΔABC = \(\frac {1}{2}\) × base × height
⇒ 30 = \(\frac {1}{2}\)(x)(x + 7)
⇒ 60 = x² + 7x
⇒ x² + 7x – 60 = 0
⇒ x² + 12x – 5x – 60 = 0
⇒ x(x + 12) – 5(x + 12) = 0
⇒ (x – 5)(x + 12) = 0
⇒ x = 5 or x = -12+
⇒ x = 5 [∵ x ≠ -12]
∴ Base (x) = 5 cm and
Altitude = x + 7 = 5 + 7 = 12 cm.

Question 2.
The cost of turfing a triangular field at the rate of ₹ 45 per 100 m² is ₹ 900. Find the height, if double the base of the triangle is 5 times the height.
Solution :
Let the height of triangular field be h metres.
It is given that 2 × (base) = 5 × (Height)
∴ Base = \(\frac {5}{2}\) h
Area = \(\frac {1}{2}\) × Base × Height
Area = \(\frac {1}{2}\) × \(\frac {5}{2}\)h × h = \(\frac {5}{4}\)h²m² …………(i)
∴ Cost of turfing the field is ₹ 45 per 100m²
∴ Area = Total cost / Rate per sq.m
= \(\frac{900}{45 / 100}=\frac{90000}{45}\)
= 2000 m² …………(ii)
From (i) and (ii), we get
\(\frac {5}{4}\)h² = 2000
⇒ 5h² = 8000
⇒ h² = 1600
⇒ h = 40 m
∴ Height of the triangular field is 40 m.

Question 3.
From a point in the interior of an equilateral triangle, perpendicular drawn to the three sides are 8 cm, 10 cm and 11 cm respectively. Find the area of the triangle.

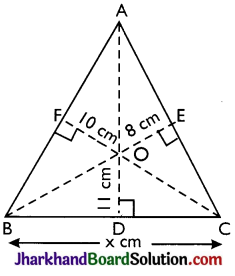
Solution :
Let each side of the equilateral ΔABC = x cm,
From an interior point O, OD, OE and OF perpendiculars be drawn to BC, AC and AB respectively.
It is given that OD = 11 cm, OE = 8 cm and OF = 10 cm.
Join OA, OB and OC.
Area of ΔABC = Area of ΔOBC + Area of ΔOCA + Area of ΔOAB
= \(\frac {1}{2}\) × 11 + \(\frac {1}{2}\) × 8 + \(\frac {1}{2}\) × 10 = \(\frac {29}{2}\) × cm²
But, area of an equilateral triangle, whose each side is x = \(\frac{\sqrt{3}}{4}\) x²cm²
Therefore,
\(\frac{\sqrt{3}}{4}\) x² = \(\frac {29}{2}\)x
∴ x = \(\frac{4 \times 29}{2 \times \sqrt{3}}=\frac{58}{\sqrt{3}}\) cm
∴ Area of ΔABC
= \(\frac{29}{2} \times \frac{58}{\sqrt{3}}\) cm² = \(\frac{\sqrt{841}}{1.73}\)cm²
∴ Area of ΔABC = 486.1 cm²

Question 4.
The difference between the sides at right angles in a right-angled triangle is 14 cm. The area of the triangle is 120 cm². Calculate the perimeter of the triangle.
Solution :
Let the sides containing the right angle be x cm and (x – 14) cm.
Then, its area = [\(\frac {1}{2}\).x. (x – 14)] cm²
But, area = 120 cm² [Given]
∴ \(\frac {1}{2}\)x (x – 14) = 120
⇒ x² – 14x – 240 = 0
⇒ x² – 24x + 10x – 240 = 0
⇒ x(x – 24) + 10 (x – 24) = 0
⇒ (x – 24) (x + 10) = 0
⇒ x = 24 [Neglecting x = -10]
∴ One side = 24 cm,
other side = (24 – 14) cm = 10 cm
Hypotenuse
= \(\sqrt{(24)^2+(10)^2}\) cm
= \(\sqrt{576+100}\) cm
= \(\sqrt{676}\) cm = 26 cm.
∴ Perimeter of the triangle
= (24 + 10 + 26) cm = 60 cm.

Question 5.
Find the percentage increase in the area of a triangle if its each side is doubled.
Solution :
Let a, b, c be the sides of the given triangle and s be its semi-perimeter
∴ s = \(\frac {1}{2}\)(a + b + c) …………(i)
The sides of the new triangle are 2a, 2b and 2c. Let s’ be its semi-perimeter.
∴ s’ = (2a + 2b + 2c)
= a + b + c = 2s [Using (i)]
Let Δ = Area of given triangle
Δ = \(\sqrt{s(s-a)(s-b)(s-c)}\) …….(ii)
And, Δ’ = Area of new triangle
Δ’ = \(\sqrt{s^{\prime}\left(s^{\prime}-2 a\right)\left(s^{\prime}-2 b\right)\left(s^{\prime}-2 c\right)}\)
= \(\sqrt{2 s(2 s-2 a)(2 s-2 b)(2 s-2 c)}\)
= \(\sqrt{16 s(s-a)(s-b)(s-c)}\)
Δ’ = 4Δ
∴ Increase in the area of the triangle
= Δ’ – Δ = 4Δ – Δ = 3Δ
∴ % increase in area = (\(\frac {3Δ}{Δ}\) × 100)%
= 300%

Multiple Choice Questions

Question 1.
The area of the field ABGFEA is:

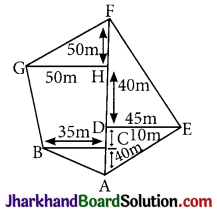
(a) 7225 m²
(b) 7230 m²
(c) 7235 m²
(d) 7240 m²
Solution :
(a) 7225 m²

Question 2.
Area of shaded portion as shown in the figure is:

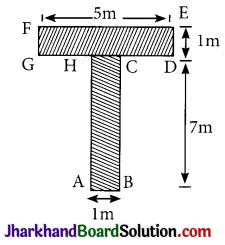
(a) 12 m²
(b) 13 m²
(c) 14 m²
(d) 15 m²
Solution :
(a) 12 m²

Question 3.
The lengths of four sides and a diagonal of the given quadrilateral are indicated in the diagram. If A denotes the area of quadrilateral in cm², then A is

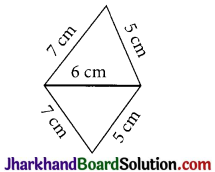
(a) 12\(\sqrt{6}\) sq. unit
(b) 6 sq. unit
(c) 6\(\sqrt{6}\) sq. unit
(d) \(\sqrt{6}\) sq. unit
Solution :
(a) 12\(\sqrt{6}\) sq. unit

Question 4.
If the sides of a triangle are doubled, then its area:
(a) Remains the same
(b) Becomes doubled
(c) Becomes three times
(d) Becomes four times
Solution :
(d) Becomes four times

Question 5.
Inside a triangular garden there is a flower bed in the form of a similar triangle. Around the flower bed runs a uniform path of such a width that the side of the garden are double of the corresponding sides of the flower bed. The areas of the path and the flower bed are in the ratio:
(a) 1 : 1
(b) 1 : 2
(c) 1 : 3
(d) 3 : 1
Solution :
(d) 3 : 1