Jharkhand Board JAC Class 9 Maths Important Questions Chapter 15 Probability Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 15 Probability
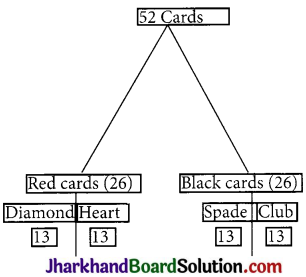
Question 1.
A card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting
(i) A king.
(ii) A heart.
(iii) A seven of heart.
(iv) A jack, queen or a king.
(v) A two of heart or a two of diamond.
(vi) A face card.
(vii) A black card.
(viii) Neither a heart nor a king,
(ix) Neither an ace nor a king.
Solution :
Total number of outcomes = 52
(i) A king
No. of kings = 4
P(A) = \(\frac{4}{52}=\frac{1}{13}\)
(ii) A heart, P(A) = \(\frac{13}{52}=\frac{1}{4}\)
(iii) A seven of heart P(A) = \(\frac{1}{52}\)
(iv) A jack, queen or a king,
P(A) = \(\frac{12}{52}=\frac{3}{13}\)
(v) A two of heat or a two of diamond,
P(A) = \(\frac{2}{52}=\frac{1}{26}\)
(vi) A face card, P(A) = \(\frac{12}{52}=\frac{3}{13}\)
(vii) A black card, P(A) = \(\frac{26}{52}=\frac{1}{2}\)
(viii) Neither a heart nor a king (13 heart + 4 king, but 1 common)
P(A) = 1 – \(\frac{16}{52}=\frac{52-16}{52}=\frac{36}{52}=\frac{9}{13}\)
(ix) Neither an ace nor a king,
P(A) = \(\frac{44}{52}=\frac{11}{13}\)
Question 2.
Two coins are tossed simultaneously. Find the probability of getting
(i) two heads
(ii) at least one head
(iii) no head
Solution :
On tossing two coins simultaneously, all the possible outcomes are HH, HT, TH, TT.
(i) The probability of getting two heads
= P (HH)
= No. of outcomes of two heads / Total no. of possible outcomes
= \(\frac {1}{4}\)
(ii) The probability of getting at least one head
= No. of favourable outcomes / Total no. of outcomes
= \(\frac {3}{4}\)
(iii) The probability of getting no head
P(TT) = \(\frac {1}{4}\)
![]()
Question 3.
A bag contains 5 red balls, 8 white balls, 4 green balls and 7 black balls. If one ball is drawn at random, find the probability that it is
(i) Black
(ii) Not red
(iii) Green
Solution :
Number of red balls in the bag = 5.
Number of white balls in the bag = 8.
Number of green balls in the bag = 4.
Number of black balls in the bag = 7.
∴ Total number of balls in the bag = 5 + 8 + 4 + 7 = 24.
Drawing balls randomly are equally likely outcomes.
∴ Total number of possible outcomes = 24.
Now,
(i) There are 7 black balls, hence the number of such favourable outcomes = 7
∴ Probability of drawing a black ball
= No. of favourable outcomes / Total no. of possible outcomes
= \(\frac {7}{24}\)
(ii) There are 5 red balls, hence the number of such favourable outcomes = 5.
∴ Probability of drawing a red ball
= No. of favourable outcomes / Total no. of possible outcomes
= \(\frac {5}{24}\)
∴ Probability of drawing not a red ball = P(Not red ball) = 1 – \(\frac{5}{24}=\frac{19}{24}\)
(iii) There are 4 green balls.
∴ Number of such favourable outcomes = 4
Probability of drawing a green ball = No. of favourable outcomes / Total no. of possible outcomes
= \(\frac{4}{24}=\frac{1}{6}\)
Question 4.
A card is drawn from a well-shuffled deck of playing cards. Find the probability of drawing
(i) a face card
(ii) a red face card
Solution :
Random drawing of cards ensures equally likely outcomes
(i) Number of face cards (King, Queen and jack of each suits) = 4 x 3 = 12.
Total number of cards in deck = 52.
∴ Total number of possible outcomes = 52.
P (drawing a face card) = \(\frac{12}{52}=\frac{3}{13}\)
(ii) Number of red face cards = 2 × 3 = 6.
Number of favourable outcomes of drawing red face card = 6.
P(drawing of red face card) = \(\frac{6}{52}=\frac{3}{26}\)
Multiple Choice Questions
Question 1.
3 Coins are tossed simultaneously. The probability of getting at least 2 heads is
(a) \(\frac {3}{10}\)
(b) \(\frac {3}{4}\)
(c) \(\frac {3}{8}\)
(d) \(\frac {1}{2}\)
Solution :
(c) \(\frac {3}{8}\)
![]()
Question 2.
Two cards are drawn successively with replacement from a pack of 52 cards. The probability of getting two aces is
(a) \(\frac {1}{169}\)
(b) \(\frac {1}{221}\)
(c) \(\frac {1}{265}\)
(d) \(\frac {1}{663}\)
Solution :
(b) \(\frac {1}{221}\)
Question 3.
In a single throw of two dice, the probability of getting a sum of more than 7 is
(a) \(\frac {7}{36}\)
(b) \(\frac {7}{12}\)
(c) \(\frac {5}{12}\)
(d) \(\frac {5}{36}\)
Solution :
(c) \(\frac {5}{12}\)
Question 4.
Two cards are drawn at random from a pack of 52 cards. The probability that both are the cards of spade is
(a) \(\frac {1}{26}\)
(b) \(\frac {1}{4}\)
(c) \(\frac {1}{17}\)
(d) None of these
Solution :
(c) \(\frac {1}{17}\)
![]()
Question 5.
Two dice are thrown together. The probability that sum of the two numbers will be a multiple of 4 is
(a) \(\frac {1}{9}\)
(b) \(\frac {1}{3}\)
(c) \(\frac {1}{4}\)
(d) \(\frac {5}{9}\)
Solution :
(c) \(\frac {1}{4}\)
Question 6.
If the three coins are simultaneously tossed compute the probability of 2 heads coming up.
(a) \(\frac {3}{8}\)
(b) \(\frac {1}{4}\)
(c) \(\frac {5}{8}\)
(d) \(\frac {3}{4}\)
Solution :
(a) \(\frac {3}{8}\)
Question 7.
A coin is tossed successively three times. The probability of getting one head or two heads is:
(a) \(\frac {2}{3}\)
(b) \(\frac {3}{4}\)
(c) \(\frac {4}{9}\)
(d) \(\frac {1}{9}\)
Solution :
(b) \(\frac {3}{4}\)
![]()
Question 8.
One card is drawn from a pack of 52 cards. What is the probability that the drawn card is either red or king:
(a) \(\frac {15}{26}\)
(b) \(\frac {1}{2}\)
(c) \(\frac {7}{13}\)
(d) \(\frac {17}{32}\)
Solution :
(c) \(\frac {7}{13}\)