Students should go through these JAC Class 9 Maths Notes Chapter 2 Polynomials will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 2 Polynomials
Polynomials:
An algebraic expression f(x) of the form f(x) = a0 + a1x + a2x2 + …… + anxn, where a0, a1, a2 ……, an are real numbers and all the index of x’ are nonnegative integers is called a polynomial in x.
→ Degree of a Polynomial: Highest Index of x in algebraic expression is called the degree of the polynomial, here a0, a1x, a2x2 ….. anxn, are called the terms of the polynomial and a0, a1, a2, …… an are called various coefficients of the polynomial f(x).
Note: A polynomial in x is said to be in standard form when the terms are written either in increasing order or decreasing order of the indices of x in various terms.
→ Different Types of Polynomials: Generally, we divide the polynomials in the following categories.
→ Based on degrees:
There are four types of polynomials based on degrees. These are listed below:
- Linear Polynomials: A polynomial of degree one is called a linear polynomial. The general form of linear polynomial is ax + b, where a and b are any real constant and a ≠ 0.
- Quadratic Polynomials: A polynomial of degree two is called a quadratic polynomial. The general form of a quadratic polynomial is ax2 + bx + c, where a ≠ 0, a, b, c ∈ R.
- Cubic Polynomials: A polynomial of degree three is called a cubic polynomial. The general form of a cubic polynomial is ax3 + bx2 + cx + d, where a ≠ 0 and a, b, c, d ∈ R.
- Biquadratic (or quadric) Polynomials: A polynomial of degree four is called a biquadratic (quadric) polynomial. The general form of a biquadratic polynomial is ax4 + bx3 + cx2 + dx + e, where a ≠ 0 and a, b, c, d, e are real numbers.
Note: A polynomial of degree five or more than five does not have any particular name. Such a polynomial usually called a polynomial of degree five or six or ….etc.
→ Based on number of terms:
There are three types of polynomials based on number of terms. These are as follow:
- Monomial: A polynomial is said to be monomial if it has only one term. e.g. x, 9x2, 5x3 all are monomials.
- Binomial: A polynomial is said to be binomial if it contains only two terms e.g. 2x2 + 3x, \(\sqrt{3}\)x + 5x3, -8x3 + 3, all are binomials.
- Trinomial: A polynomial is said to be a trinomial if it contains only three terms.e.g. 3x3 – 8x + \(\frac{1}{2}\), \(\sqrt{7}\) x10 + 8x4 – 3x2, 5 – 7x + 8x9, are all trinomials.
Note: A polynomial having four or more than four terms does not have particular name. These are simply called polynomials.
→ Zero degree polynomial: Any non-zero number (constant) is regarded as polynomial of degree zero or zero degree polynomial. i.e. f(x) = a. where a ≠ 0 is a zero degree polynomial, since we can write f(x) = a, as f(x) = ax0.
→ Zero polynomial: A polynomial whose all coefficients are zero is called as zero polynomial i.e. f(x) = 0, we cannot determine the degree of zero polynomial.
![]()
Algebraic Identities:
An identity is an equality which is true for all values of the variables.
Some important identities are:
(i) (a + b)2 = a2 + 2ab + b2
(ii) (a – b)2 = a2 – 2ab + b2
(iii) a2 – b2 = (a + b)(a – b)
(iv) a3 + b3 = (a + b)(a2 – ab + b2)
(v) a3 – b3 = (a – b)(a2 + ab + b2)
(vi) (a + b)3 = a3 + b3 + 3ab (a + b)
(vii) (a – b)3 = a3 – b3 – 3ab (a – b)
(viii) a4 + a2b2 + b4 = (a2 + ab + b2)(a2 – ab + b2)
(ix) a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ac)
Special case: if a + b + c = 0 then a3 + b3 + c3 = 3abc.
Other Important Identities
(i) a2 + b2 = (a + b)2 – 2ab,
if a + b and ab are given
(ii) a2 + b2 = (a – b)2 + 2ab
if a – b and ab are given
(iii) a + b = \(\sqrt{(a-b)^2+4 a b}\)
if a – b and ab are given
(iv) a – b = \(\sqrt{(a+b)^2-4 a b}\)
if a + b and ab are given
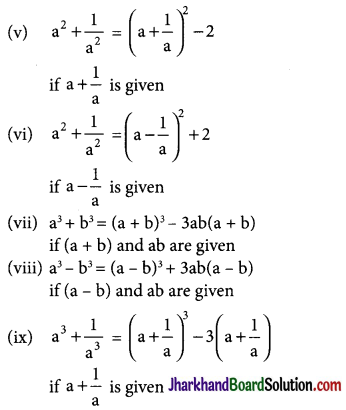
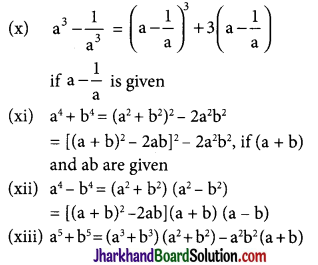
Factors Of A Polynomial:
→ If a polynomial f(x) can be written as a product of two or more other polynomials f1(x), f2(x), f3(x)…. then each of the polynomials f1(x), f2(x), f3(x)….. is called a factor of polynomial f(x). The method of finding the factors of a polynomial is called factorisation.
![]()
Zeroes Of A Polynomial:
→ A real number α is a zero of polynomial f(x) = anxn + an-1xn-1 + an-2xn-2 + ….. +a1x + a0, if f(α) = 0. i.e. anαn + an-1αn-1 + an-2αn-2+ ….. + a1α + a0 = 0.
For example x = 3 is a zero of the polynomial f(x) = x3 – 6x2 + 11x – 6, because f(3) = (3)3 – 6(3)2 + 11(3) – 6 = 27 – 54 + 33 – 6 = 0.
but x = -2 is not a zero of the above mentioned polynomial,
∵ f(-2) = (-2)3 – 6(-2)2 + 11(-2) – 6
f(-2) = -8 – 24 – 22 – 6
f(-2) = -60 ≠ 0.
→ Value of a Polynomial: The value of a polynomial f(x) at x = a is obtained by substituting x a in the given polynomial and is denoted by f(a). Eg if f(x) = 2x3 – 13x2 + 17x + 12 then its value at x = 1 is
f(1) = 2(1)3 – 13(1)2 + 17(1) + 12
= 2 – 13 + 17 + 12 = 18.
Remainder Theorem:
Let ‘p(x)’ be any polynomial of degree greater than or equal to one and ‘a’ be any real number and if p(x) is divided by (x – a). then the remainder is equal to p(a). Let q(x) be the quotient and r(x) be the remainder when p(x) is divided by (x – a), then
Dividend = Divisor × Quotient + Remainder
∴ p(x) = (x – a) × q(x) + [r(x) or r], where r(x) = 0 or degree of r(x) < degree of (x – a). But (x – 2) is a polynomial of degree 1 and a polynomial of degree less than 1 is a constant. Therefore, either r(x) = 0 or r(x) = Constant. Let r(x) = r, then p(x) = (x – a)q(x) + r.
Putting x = a in above equation, p(a)
p(a) = (a – a)q(a) + r = 0 × q(a) + r
p(a) = 0 + r
⇒ p(a) = r
This shows that the remainder is p(a) when p(x) is divided by (x – a).
Remark: If a polynomial p(x) is divided by (x + a),(ax – b), (ax + b), (b – ax) then the remainder is the value of p(x) at x.
= \(-a, \frac{b}{a},-\frac{b}{a}, \frac{b}{a} \text { i.e. } p(-a)\)
\(p\left(\frac{b}{a}\right), p\left(-\frac{b}{a}\right), p\left(\frac{b}{a}\right)\) respectively.
Factor Theorem:
Let ‘p(x)’ be a polynomial of degree greater than or equal to 1 and ‘a’ be a real number such that p(a) = 0, then (x – a) is a factor of p(x). Conversely, if(x – a) is a factor of p(x). then p(a) = 0.
![]()
Factorisation Of A Quadratic Polynomial:
→ For factorisation of a quadratic expression ax2 + bx + c where a ≠ 0, there are two methods.
→ By Method of Completion of Square:
In the form ax2 + bx + c where a ≠ 0, firstly we take ‘a’ common in the whole expression then factorise by converting the expression \(a\left\{x^2+\frac{b}{a} x+\frac{c}{a}\right\}\) as the difference of two squares, which is

→ By Splitting the Middle Term:
→ x2 + lx + m = x2 + (a + b)x + ab
Where l = a + b and m = ab, such that a and b are real numbers
= x2 + ax + bx + ab
= x (x + a) + b (x + a)
= (x + a) (x + b)
Method: We express l as the sum of two such numbers whose product is m.
→ ax2 + bx + c = prx2 + (ps + qr)x + qs
where b = ps + qr, a = pr, c = qs
so that (ps) (gr) (pr) (qs) = ac
∴ prx2 + (ps + qr)x + qs
= prx2 + psx + qrx + qs
= px (rx + s) + q(rx + s)
= (px + q) (rx + x)
Method: We express b as the sum of two such numbers whose product is ac.
→ Integral Root Theorem:
If f(x) is a polynomial with integral coefficient and the leading coefficient is 1, then any integral root of f(x) is a factor of the constant term. Thus if f(x) = x3 – 6x2 + 11x – 6 has an Integral root, then it is one of the factors of 6 which are ±1, ±2, ±3, ±6.
Now in fact,
f(1) = (1)3 – 6(1)2 + 11(1) – 6 = 1 – 6 + 11 – 6 = 0
f(2) = (2)3 – 6(2)2 + 11(2) – 6
= 8 – 24 + 22 – 6 = 0
f(3) = (3)3 – 6(3)2 + 11(3) – 6
27 – 54 + 33 – 6 = 0
Therefore Integral roots of f(x) are 1, 2, 3.
![]()
→ Rational Root Theorem:
Let \(\frac{b}{c}\) be a rational fraction in lowest terms. If \(\frac{b}{c}\) is a rational root of the polynomial f(x) = anxn + an-1xn-1 +…+ a1x + a0, an ≠ 0 with integral coefficients, then b is a factor of constant term a0, and C is a factor of the leading coefficient an.
For example: If \(\frac{b}{c}\) is a rational root of the polynomial f(x) = 6x3 + 5x2 – 3x – 2, then the values of b are limited to the factors of -2, which are ±1, ±2 and the values of care limited to the factors of 6, which are ±1, ±2, ±3, ±6. Hence, the possible rational roots of f(x) are ±1, ±2, \(\pm \frac{1}{2}, \pm \frac{1}{3}, \pm \frac{1}{6}, \pm \frac{2}{3}\). In fact -1 is an integral root and \(\frac{2}{3}\), –\(\frac{1}{2}\) are the rational roots of f(x) = 6x3 + 5x2 – 3x – 2.
Note: (i) nth degree polynomial can have at most n real roots.
→ Finding a zero of polynomial f(x) means solving the polynomial equation f(x) = 0. It follows from the above discussion that if f(x) = ax + b, a ≠ 0 is a linear polynomial, then it has only one zero given by
f(x) = 0 i.e. f(x) = ax + b = 0
⇒ ax = -b
⇒ x = –\(\frac{b}{a}\)
Thus, x = –\(\frac{b}{a}\) is the only zero of f(x) = ax + b.
→ If a polynomial of degree n has more than n zeros then all the coefficients of powers of x including constant term of polynomial are zero.