Students should go through these JAC Class 9 Maths Notes Chapter 7 Triangles will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 7 Triangles
Triangle
A plane figure bounded by three lines in a plane is called a triangle. Every triangle has three sides and three angels. If ABC is any triangle then AB, BC and CA are three sides and ∠A, ∠B and ∠C are three angles.
Types of Triangles
→ On the basis of sides we have three types of triangles:
- Scalene triangle – A triangle whose no two sides are equal is called a scalene triangle.
- Isosceles triangle – A triangle having two sides equal is called an isosceles triangle.
- Equilateral triangle – A triangle in which all sides are equal is called an equilateral triangle.
→ On the basis of angles we have three types of triangles:
- Right triangle – A triangle in which any one angle is a right angle (= 90°) is called right triangle.
- Acute triangle – A triangle in which all angles are acute (0° >angle >90°) is called an acute triangle.
- Obtuse (90° < angle < 180° ) triangle – A triangle in which any one angle is obtuse is called an obtuse triangle.
Congruent Figures
The figures are called congruent if they have same shape and same size. In other words, two figures are called congruent if they are having equal length, width and height.

In the above figures {Fig. (i) and Fig. (ii)} both are equal in length, width and height, so these are congruent figures.
![]()
Congruent Triangles
Two triangles are congruent if and only if one of them can be made to superimposed on the other, so as to cover it exactly.
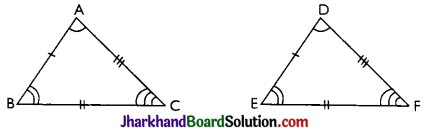
If two triangles ΔABC and ΔDEF are congruent then there exist a one to one correspondence between their vertices and sides. i.e. we get following six equalities.
∠A = ∠D, ∠B = ∠E, ∠C = ∠F and AB = DE, BC = EF, AC = DF.
If ΔABC and ΔDEF are congruent under one to one correspondence A ↔ D, B ↔ E, C ↔ F then we write ΔABC ≅ ΔDEF We cannot write it as ΔABC ≅ ΔDFE or ΔABC ≅ ΔEDF or in other forms because ΔABC ≅ ΔDFE have following one-one correspondence A ↔ D, B ↔ F, C ↔ E.
Hence, we can say that ‘two triangles are congruent if and only if there exists a oneone correspondence between their vertices such that the corresponding sides and the corresponding angles of the two triangles are equal.
Sufficient Conditions for Congruence of two Triangles
→ SAS Congruence Criterion:
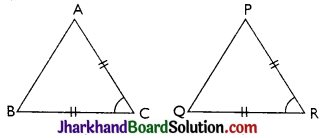
Two triangles are congruent if two sides and the included angle of one triangle are equal to the corresponding sides and the included angle of the other triangle.
→ ASA Congruence Criterion:
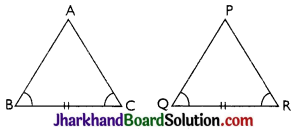
Two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle.
→ AAS Congruence Criterion:
If any two angles and a non included side of one triangle are equal to the corresponding angles and side of another triangle, then the two triangles are congruent.
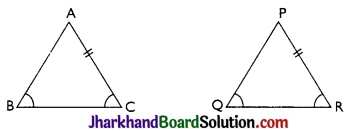
→ SSS Congruence Criterion:
Two triangles are congruent if the three sides of one triangle are equal to the corresponding three sides of the other triangle.
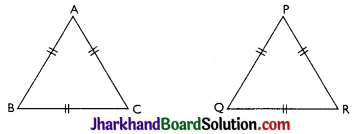
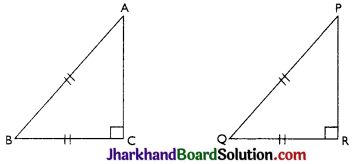
→ RHS Congruence Criterion:
Two right angled triangles are congruent if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and one side of the other triangle.
→ Congruence Relation in the Set of all Triangles:
By the definition of congruence of two triangles, we have following results.
- Every triangle is congruent to itself i.e., ΔABC ≅ ΔABC
- If ΔABC ≅ ΔDEF then ΔDEF ≅ ΔABC
- If ΔABC ≅ ΔDEF and ΔDEF ≅ ΔΡQR then ΔΑΒC ≅ ΔΡQR
NOTE: If two triangles are congruent then their corresponding sides and angles are also congruent by CPCT (corresponding parts of congruent triangles are also congruent).
![]()
Theorem 1.
Angles opposite to equal sides of an isosceles triangle are equal.
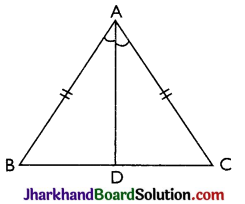
Given:
ΔABC in which AB = AC
To Prove: ∠B = ∠C
Construction: We draw the bisector AD of ∠A which meets BC in D.
Proof: In ΔABD and ΔACD, we have
AB = AC [Given]
∠BAD = ∠CAD [∵ AD is bisector of ∠A]
And, AD = AD [Common side]
∴ By SAS criterion of congruence, we have
ΔΑΒD ≅ ΔΑCD
⇒ ∠B = ∠C [by CPCT]
Hence, proved.
Theorem 2.
If two angles of a triangle are equal, then sides opposite to them are also equal.
Given: ΔABC in which ∠B = ∠C
To Prove: AB = AC
Construction: We draw the bisector of ∠A
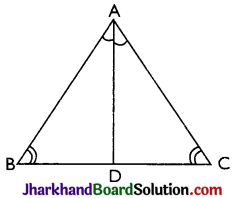
which meets BC in D.
Proof: In ΔABD and ΔACD, we have
∠B = ∠C [Given]
∠BAD = ∠CAD [∵ AD is bisector of ∠A]
AD = AD [Common side]
∴ By AAS criterion of congruence, we get
ΔΑΒD ≅ ΔΑCD
⇒ AB = AC [By CPCT] Hence, proved.
Theorem 3.
If the bisector of the vertical angle bisects the base of the triangle, then the triangle is isosceles.
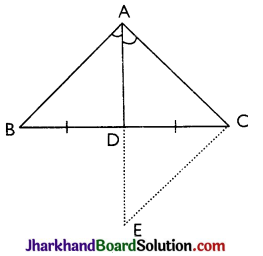
Given: ΔABC in which AD is the bisector of ∠A meeting BC in D such that BD = CD
To Prove: ΔABC is an isosceles triangle.
Construction: We produce AD to E such that AD = DE and join EC
Proof: In ΔADB and ΔEDC, we have
AD = DE [By construction]
∠ADB = ∠CDE [Vertically opposite angles]
BD = DC [Given]
∴ By SAS criterion of congruence, we get
ΔADR ≅ ΔEDC ⇒ AB = EC ……(i)
And, ∠BAD = ∠CED [By CPCT]
But, ∠BAD = ∠CAD
∴ ∠CAD = ∠CED
⇒ AC = EC [Sides opposite to equal angles are equal]
⇒ AC = AB [By eq. (i)] Hence, proved
![]()
Some Inequality Relations In A Triangle
→ If two sides of a triangle are unequal, then the longer side has greater angle opposite to it, i.e., if in any ΔABC, AB > AC then ∠C > ∠B.
→ In a triangle the greater angle has the longer side opposite to it, ie, if in any ΔABC, ∠A > ∠B then BC > AC.
→ The sum of any two sides of a triangle is always greater than the third side, i.e., in any ΔABC, AB + BC > AC, BC + CA > AB and AC + AB > BC.
→ Of all the line segments that can be drawn to a given line, from a point, not lying on it, the perpendicular line segment is the shortest.
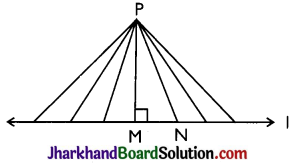
P is any point not lying on line l, PM ⊥ l then PM < PN.
→ The difference of any two sides of a triangle is less than the third side, i.e., in any ΔABC, AB – BC < AC, BC – CA < AB and AC – AB < BC.