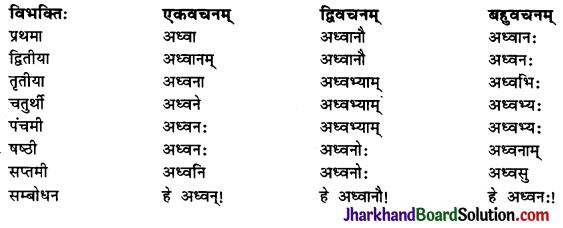
Jharkhand Board JAC Class 10 Sanskrit Solutions Shemushi Chapter 3 व्यायामः सर्वदा पथ्यः Textbook Exercise Questions and Answers.
JAC Board Class 10th Sanskrit Solutions Shemushi Chapter 3 व्यायामः सर्वदा पथ्यः
JAC Class 10th Sanskrit व्यायामः सर्वदा पथ्यः Textbook Questions and Answers
प्रश्न 1.
एकपदेन उत्तरं लिखत- (एक शब्द में उत्तर लिखिए-)
(क) परमम् आरोग्यं कस्मात् उपजायते ? (परमारोग्य किससे होता है?)
(ख) कस्य मासं स्थिरीभवति? (किसका मांस स्थिर होता है?)
(ग) सदा कः पथ्य? (सदा क्या अनुकूल है?)
(घ) कै पुभिः सर्वेषु ऋतुषु व्यायामः कर्त्तव्यः? (किन लोगों को सभी ऋतुओं में व्यायाम करना चाहिए?)
(ङ) व्यायामस्विन्नगात्रस्य समीपं के न उपसर्पन्ति? (व्यायाम से उत्पन्न पसीना वाले शरीर के समीप कौन नहीं आते?)
उत्तरम्म् :
(क) व्यायामात् (व्यायाम से)।
(ख) व्यायामाभिरतस्य (व्यायाम में लगे हुए का)
(ग) व्यायामः (कसरत)।
(घ) पुम्भिरात्महितैषिभिः (अपना हित चाहने वालों को)।
(ङ) व्याधयः (रोग)।
प्रश्न 2.
अधोलिखितानां प्रश्नानाम् उत्तराणि संस्कृतभाषया लिखत –
(निम्नलिखित प्रश्नों के उत्तर संस्कृत भाषा में लिखिए)
(क) कीदृशं कर्म व्यायामसंज्ञितं कथ्यते ?
(कैसा कर्म व्यायाम नाम से पुकारा जाता है ?)
उत्तरम् :
शरीरायासजननं कर्म व्यायामसंज्ञितं कथ्यते।
(शरीर को थकाने वाला कर्म व्यायाम कहलाता है।)

(ख) व्यायामात् किं किमुपजायते ?
(व्यायाम से क्या पैदा होता है ?)
उत्तरम् :
शरीरोपचयः, कान्तिः, गात्राणां सुविभक्तता, दीप्ताग्नित्वम्, अनालस्यं, स्थिरत्वं, लाघवं, मृजा, श्रमक्लमपिपासा, उष्ण-शीतादीनां सहिष्णुता परमं च आरोग्यम् व्यायामात् उपजायते।
(शरीर की वृद्धि, चमक, सुडौलता, दीप्ति, पाचनशक्ति की वृद्धि, आलस्यहीनता, स्थिरता, फुर्ती, स्वच्छता, परिश्रम, थकान, प्यास, गर्मी-सर्दी आदि को सहन करने की क्षमता और महान स्वस्थता व्यायाम से उत्पन्न होती है। )
(ग) जरा कस्य सकाशं सहसा न समधिरोहति ?
(बुढ़ापा अचानक किस पर हावी नहीं होता ?)
उत्तरम् :
व्यायामाभिरतस्य सकाशं जरा सहसा न समधिरोहति।
(व्यायाम में संलग्न के पास बुढ़ापा अचानक नहीं आता।)
(घ) कस्य विरुद्धमपि भोजनं परिपच्यते?
(किसका विरुद्ध भोजन भी पचता है?)
उत्तरम् :
व्यायामम् कुर्वतः नित्यं विरुद्धमपि भोजनं परिपच्यते।
(व्यायाम करते हुए का विरुद्ध भोजन भी पचता है।)
(ङ) कियता बलेन व्यायामः कर्त्तव्यः ?
(कितने बल से व्यायाम करना चाहिए ?)
उत्तरम् :
अर्धनबलेन व्यायामः कर्त्तव्यः।
(आधे बल से व्यायाम करना चाहिए।)

(च) अर्धबलस्य लक्षणं किम् ?
(आधे बल का लक्षण क्या है ?)
उत्तरम् :
यदा व्यायामं कुर्वतः हृदिस्थानस्थितो वायुः वक्त्रं प्रपद्यते, तद् बलार्धस्य लक्षणम्।
(जब व्यायाम करने वाले के हृदय में स्थित वायु मुख की ओर प्रवृत्त हो जाती है वह आधे बल का लक्षण है।)
प्रश्न 3.
उदाहरणमनुसृत्य कोष्ठकगतेषु पदेषु तृतीयाविभक्तिं प्रयुज्य रिक्तस्थानानि पूरयत –
(उदाहरण के अनुसार कोष्ठक में दिए शब्दों में तृतीया विभक्ति लगाकर प्रयोग कीजिए)
यथा – व्यायामः ……….. हीनमपि सुदर्शनं करोति। (गुण)
व्यायामः गुणैः हीनमपि सुदर्शनं करोति।
(क) ……….. व्यायामः कर्त्तव्यः। (बलस्यार्ध)
उत्तरम् :
बलस्यार्धेन व्यायामः कर्त्तव्यः।
(आधे बल से व्यायाम करना चाहिए।)
(ख) ……….. सदृशं किञ्चित् स्थौल्यापकर्षणं नास्ति। (व्यायाम)।
उत्तरम् :
व्यायामेन सदृशं किञ्चित् स्थौल्यापकर्षणं नास्ति।
(व्यायाम के समान कुछ भी मोटापा दूर करने वाला नहीं है।)
(ग) ……….. विना जीवनं नास्ति। (विद्या)
उत्तरम् :
विद्यया विना जीवनं नास्ति।
(विद्या के बिना जीवन नहीं है।)

(घ) सः ……….. खञ्जः अस्ति। (चरण)
उत्तरम् :
सः चरणेन खञ्जः अस्ति।
(वह पैर से लँगडा है।)
(ङ) सूपकारः ……….. भोजनं जिघ्रति। (नासिका)
उत्तरम् :
सूपकारः नासिकया भोजनं जिघ्रति।
(रसोइया नाक से भोजन सूंघता है।)
प्रश्न 4.
(अ) स्थूलपदमाधृत्य प्रश्ननिर्माणं कुरुत (मोटे शब्दों के आधार पर प्रश्नों का निर्माण कीजिए)
(क) शरीरस्य आयासजननं कर्म व्यायामः इति कथ्यते। (शरीर को थकाने वाला कर्म व्यायाम कहलाता है।)
(ख) अरयः व्यायामिनं न अर्दयन्ति। (शत्रु व्यायामी को नहीं कुचलते।)
(ग) आत्महितैषिभिः सर्वदा व्यायामः कर्त्तव्यः। (आत्महितैषियों द्वारा हमेशा व्यायाम करना चाहिए।)
(घ) व्यायाम कुर्वतः विरुद्धं भोजनम् अपि परिपच्यते। (व्यायाम करने वाले को विपरीत भोजन भी पच जाता है।)
(ङ) गात्राणां सुविभक्तता व्यायामेन संभवति। (अंगों का अच्छा विभाजन व्यायाम से संभव होता है।)
उत्तरम् :
(क) कस्य आयासजननं कर्म व्यायाम इति कथ्यते ? (किसको थकाने वाला कर्म व्यायाम कहलाता है ?)
(ख) के व्यायामिनं न अर्दयन्ति ? (कौन व्यायामी को नहीं कुचलते ?)
(ग) कैः सर्वदा व्यायामः कर्त्तव्यः ? (किन्हें हमेशा व्यायाम करना चाहिए ?)
(घ) व्यायाम कुर्वतः कीदृशं भोजनम् अपि परिपच्यते ? (व्यायाम करने वाले को कैसा भोजन भी पच जाता है ?)
(ङ) केषां सुविभक्तता व्यायामेन सम्भवति ? (किनकी सुविभक्तता व्यायाम से सम्भव होती है ?)
(आ) षष्ठश्लोकस्य भावमाश्रित्य रिक्तस्थानानि पूरयत – (छठे श्लोक के भाव पर आश्रित रिक्तस्थानों की पूर्ति कीजिए)
यथा : ………. समीपे उरगाः न ………. एवमेव व्यायामिनः जनस्य समीपं ……………………. न गच्छन्ति। व्यायामः वयोरूपगुणहीनम् अपि जनम् ………. करोति।
उत्तरम् :
यथा – वैनतेयसमीपे उरगाः न उपसर्पन्ति एवमेव व्यायामिनः जनस्य समीपे व्याधयो न गच्छन्ति। व्यायामः वयोरूपगुणहीनम् अपि जनम् सुदर्शनम् करोति। (जैसे गरुड़ के समीप साँप नहीं आते वैसे ही व्यायामी व्यक्ति के समीप रोग नहीं आते हैं। व्यायाम उम्र, रूप और गुणहीन को भी सुन्दर कर (बना) देता है।)

प्रश्न 5.
(अ) ‘व्यायामस्य लाभाः’ इति विषयम् अधिकृत्य पञ्चवाक्येषु ‘संस्कृतभाषया’ एकम् अनुच्छेदं लिखत।
(‘व्यायाम के लाभ’ इस विषय पर पाँच वाक्यों में संस्कृत भाषा में एक अनुच्छेद लिखिए।)
उत्तरम् :
व्यायामात् शरीरोपचयः, कान्तिः, अङ्गानां सुविभाजनं, दीप्तिः, जठराग्निवृद्धिः, आलस्यहीनता, स्थिरता, स्फूर्तिः, स्वच्छता, पिपासा, उष्ण-शीतादीनां सहिष्णुता आरोग्यं च उपजायते। व्यायामः मनुष्यस्य पीनत्वं दूरं करोति, जरागमनं अवरोधयति। व्यायामिनः व्याधयो नोपसर्पन्ति। तस्य गरिष्ठभोजनमपि पचति। व्यायामेन मनुष्यः गुणहीनः अपि सुदर्शनः भवति। (व्यायाम से शरीर की वृद्धि, चमक, अंग-विभाजन, भूख-वृद्धि, आलस्यहीनता, स्थिरता, फुर्ती, स्वच्छता, प्यास, सर्दी-गर्मी को सहन करने की सामर्थ्य और नीरोगता होती है। व्यायाम मनुष्य के मोटापे को दूर करता है, बुढ़ापे को आने से रोकता है। व्यायाम करने वाले के पास रोग नहीं आते। उसको गरिष्ठ भोजन भी पचता है। व्यायाम से मनुष्य गुणहीन होते हुए भी सुन्दर होता है।)
(आ) यथा निर्देशमुत्तरत (निर्देशानुसार उत्तर दीजिए)
(क) ‘तत्कृत्वा तु सुखं देहम्’ अत्र विशेषण पदं किम्?
(‘उसे करके सुखी शरीर होता है’ यहाँ विशेषण पद क्या है?)
(ख) ‘व्याधयोः नोपसर्पन्ति वैनतेयमिवोरगाः।’ अस्मिन् वाक्ये क्रियापदं किम्?’
(‘रोग ऐसे समीप नहीं आते जैसे गरुड़ के पास सर्प’ इस वाक्य में क्रियापद क्या है?)
(ग) ‘पुम्भिरात्महितैषिभिः’ अत्र ‘पुरुषैः’ इत्यर्थे किं पदं प्रयुक्तम्?
(‘हित चाहने वाले पुरुषों द्वारा’ यहाँ ‘पुरुषैः’ अर्थ में कौन-सा पद प्रयोग हुआ है?)
(घ) ‘दीप्ताग्नित्वमनालस्यं स्थिरत्वं लाघं मृजा’ इति वाक्यात् ‘गौरवम्’ इति पदस्य विपरीतार्थकं पदं चित्वा लिखत।’
(जठराग्निदीपन, अनालस्य, स्थिरता, हलकापन, सफाई इस वाक्य से गौरवम् पद का विलोम चुनकर लिखिए)
(ङ) ‘न चास्ति सदृशं तेन किञ्चित् स्थौल्यापकर्षणम्’ अस्मिन् वाक्ये ‘तेन’ इति सर्वनाम पदं कस्मै प्रयुक्तम्?
(‘उसके समान मुटापे को दूर करने वाला और कुछ नहीं’ इस वाक्य में ‘तेन’ सर्वनाम पद किसके लिए प्रयोग हुआ है?)
उत्तराणि :
(क) सुखम् (देहं का विशेषण)
(ख) उपसर्पन्ति (पास आती है)
(ग) पुम्भिः (पुमान् शब्द का तृतीया विभक्ति बहुवचन)
(घ) लाघवम् (हल्कापन)
(ङ) व्यायामेन (व्यायाम के समान)।

प्रश्न 6.
(अ) निम्नलिखितानाम् अव्ययानां रिक्तस्थानेषु प्रयोगं कुरुत – (निम्नलिखित अव्ययों को रिक्तस्थानों में प्रयोग कीजिए)
सहसा, अपि, सदृशं, सर्वदा, यदा, सदा, अन्यथा।
(क) …………. व्यायामः कर्त्तव्यः।
(ख) ………….. मनुष्यः सम्यक्पे ण व्यायामं करोति तदा सः ………. स्वस्थः तिष्ठति।
(ग) व्यायामेन असुन्दराः ………. सुन्दराः भवन्ति।
(घ) व्यायामिनः जनस्य सकाशं वार्धक्यं ………. नायाति।
(ङ) व्यायामेन ………. किञ्चित् स्थौल्यापकर्षणं नास्ति।
(च) व्यायाम समीक्ष्य एव कर्तव्यम् ………. व्याधयः आयान्ति।
उत्तरम् :
(क) सदा
(ख) यदा, सर्वदा
(ग) अपि
(घ) सहसा
(ङ) सदृशम्
(च) अन्यथा।
(आ) उदाहरणमनुसृत्य वाच्यपरिवर्तनं कुरुत (उदाहरण के अनुसार वाच्य परिवर्तन कीजिए)

प्रश्न 7.
अधोलिखितेषु तद्धितपदेषु प्रकृति/प्रत्ययं च पृथक् कृत्वा लिखत –
(निम्नलिखित तद्धित पदों में प्रकृति/प्रत्यय अलग-अलग करके लिखिए) –
उत्तरम् :

योग्यताविस्तार यह पाठ आयुर्वेद के प्रसिद्ध ग्रन्थ ‘सुश्रुतसंहिता’ के चिकित्सा स्थान में वर्णित 24वें अध्याय से संकलित है। इसमें आचार्य सुश्रुत ने व्यायाम की परिभाषा बताते हुए उससे होने वाले लाभों की चर्चा की है। शरीर में सुगठन, कान्ति, स्फूर्ति, सहिष्णुता, नीरोगता आदि व्यायाम के प्रमुख लाभ है।
(क) सुश्रुत: आयुर्वेदस्य, सुश्रुतसंहिताश इत्याख्यस्य ग्रन्थस्य रचयिता। अस्मिन् ग्रन्थे शल्यचिकित्सायाः प्राधान्यमस्ति। सुश्रुतः शल्याशास्त्रज्ञय दिवोदासस्य शिष्यः आसीत्। दिवोदासः सुश्रुतं वाराणस्याम् आयुर्वेदम् अपाठयत्। सुश्रुतः दिवोदासस्य उपदेशान् स्वग्रन्थेऽलिखत्।

(ख) उपलब्धासु आयुर्वेदीय-संहितासु ‘सुश्रुतसंहिता’ सर्वश्रेष्ठः शल्यचिकित्साप्रधानो ग्रन्थः। अस्मिन् ग्रन्थे 120 अध्यायेषु क्रमेण सुत्रस्थाने मौलिकसिद्धान्तानां शल्यकर्मोपयोगि-यन्त्रादीनां, निदानस्थाने प्रमुखाणां रोगाणां, शरीरस्थाने शरीरशास्त्रस्य चिकित्सास्थाने, शल्यचिकित्साया: कल्पस्थाने च विषाणां प्रकरणानि वर्णितानि। अस्य उत्तरमतंत्रे 66 अध्यायाः सन्ति।
(ग) वैनतेयमिवोरगा: – कश्यप ऋषि की दो पत्नियाँ थीं-कट्ठ और विनता। विनता का पुत्र गरुड़ और कट्ठ का पुत्र सर्प थे। विनता का पुत्र होने के कारण गरुड़ को वैनतेय कहा जाता है। (विनतायाः अयम् वैनतेयः ढक (एय) प्रत्यये कृते)। गरुड़ सर्प से अधिक ताकतवर होता है, भयवश साँप गरुड़ के पास जाने का साहस नहीं करता। यहाँ व्यायाम करने वाले मनुष्य की तुलना गरुड़ से तथा व्याधियों की तुलना साँप से की गई है। जिस प्रकार गरुड़ के समक्ष साँप नहीं जाते। उसी प्रकार व्यायाम करने वाले व्यक्ति के पास रोग नहीं फटकते।
भाषिकविस्तार: गुणवाचक शब्दों से भाव अर्थ में ष्यज् अर्थात् य प्रत्यय लगाकर भाववाची पदों का निर्माण किया जाता है। शब्द के प्रथम स्वर में वृद्धि होती है और अन्तिम अ का लोप होता है।
(क) शूरस्य भावः शौर्यम् – शूर + ष्यज्
(ख) सुन्दरस्य भावः सौन्दर्यम् – सुन्दर + ष्यज्
(ग) सुखंस्य भावः सौख्यम् – सुख + ष्य
(घ) विदुषः भावः वैदुष्यम् – विद्वस् + ष्यज्
(ड) मधुरस्य भावः माधुर्यम् – मधुर + ष्यज्
(च) स्थूलस्य भावः स्थौल्यम् – स्थूल + ष्यज्
(छ) अरोगस्य भावः आरोग्यम् – अरोग + ष्यज्
(ज) सहितस्य भावः साहित्यम् – सहित + ष्यज्

थाल्-प्रत्यय – ‘प्रकार’ अर्थ में थाल प्रत्यय का प्रयोग होता है।
जैसे – तेन प्रकारेण – तथा
येन प्रकारेण – यथा
अन्येन प्रकारेण – अन्यथा
सर्वप्रकारेण – सर्वथा
उभयकारेण – उभयथा
भावविस्तार:
(क) शरीरमाद्यं खलु धर्मसाधनम्।
(ख) लाघवं कर्मसामर्थ्य स्थैर्य क्लेशसहिष्णुता।
दोषक्षयोऽग्निवृद्धिश्च व्यायामदुपजायते।
(ग) यथा शरीरस्य रक्षायै उचितं भोजनम्, उचितश्च व्यवहारः आवश्यकोऽस्ति तथैव शरीरस्य स्वास्थाय व्यायामः अपि आवश्यक।
(घ) युक्ताहारविहारस्य युक्तचेष्टस्य कर्मसु।
युक्तस्वप्नावबोधस्य योगो भवति दुःखहा।
(ड) पक्षिण: आकाशे उड्डीयन्तं तेषाम् उड़यनमेव तेषां व्यायामः। पशवोऽपि इतस्तत: पलायन्ते पलायनमेव तेषां व्यायामः।
शैशवे शिशुः स्वहस्तपादौ चालयति, अयमेव तस्य व्यामामः।
वि + आ + यम् धातोः घञ् प्रत्ययात् निष्पन्नः ‘व्यायाम’ शब्दः विस्तारस्य विकासस्य च वाचकः। यतो हि व्यायामेन अङ्गानां विकासः भवति। अतः सुखपूर्वकं जीवनं यापयितुं मनुष्यैः नित्यं व्यायामः करणीयः।
JAC Class 10th Sanskrit व्यायामः सर्वदा पथ्यः Important Questions and Answers
शब्दार्थ चयनम् –
अधोलिखित वाक्येषु रेखांकित पदानां प्रसङ्गानुकूलम् उचितार्थ चित्वा लिखत –
प्रश्न 1.
शरीरायासजननं कर्म व्यायामसंज्ञितम्।
(अ) कार्यम्
(ब) व्यायाम
(स) संज्ञितम्
(द) सुखम्
उत्तर :
(अ) कार्यम्

प्रश्न 2.
शरीरोपचयः कान्तिर्गात्राणां सुविभक्तता –
(अ) सुविभक्तता
(ब) दीप्ताग्नित्वम्
(स) अङ्गगानाम्
(द) लाघवं
उत्तर :
(स) अङ्गगानाम्
प्रश्न 3.
श्रमक्लमपिपासोष्ण-शीतादीनां सहिष्णुता –
(अ) सहत्वं
(ब) श्रमक्लमः
(स) सहिष्णुता
(द) उपजायते
उत्तर :
(अ) सहत्वं
प्रश्न 4.
न चास्ति सदृशं तेन किञ्चित्स्थौल्यापकर्षणम् –
(अ) सदृशं
(ब) तुल्यं
(स) व्यायामिनम्
(द) मर्त्यम्
उत्तर :
(ब) तुल्यं
प्रश्न 5.
व्याधयो नोपसर्पन्ति वैनतेयमिवोरगा: –
(अ) च पद्भ्याम्
(ब) वैनतेयम्
(स) कुर्यात्
(द) समीपं न आयान्ति
उत्तर :
(द) समीपं न आयान्ति

प्रश्न 6.
व्यायामं कुर्वतो नित्यं विरुद्धमपि भोजनम् –
(अ) अशनम्
(ब) कुर्वतः
(स) विरुद्धम्
(द) परिपच्यते
उत्तर :
(अ) अशनम्
प्रश्न 7.
व्यायामो हि सदा पथ्यो बलिनां स्निग्धभोजिनाम् –
(अ) बलिनाम्
(ब) बलवतां
(स) व्यायामो हि
(द) स्मृतः
उत्तर :
(ब) बलवतां
प्रश्न 8.
बलस्यार्धन कर्त्तव्यो व्यायामो हन्त्यतोऽन्यथा –
(अ) ऋतुषु
(ब) नाशयति
(स) पुम्भिः
(द) अतोऽन्यथाः
उत्तर :
(ब) नाशयति

प्रश्न 9.
व्यायामं कुर्वतो जन्तोस्तबलार्धस्य लक्षणम् –
(अ) प्रपद्यते
(ब) वक्त्रम्
(स) संकेतम्
(द) लक्षणम्
उत्तर :
(स) संकेतम्
प्रश्न 10.
समीक्ष्य कुर्याद् व्यायाममन्यथा रोगमाप्नुयात्
(अ) च देश
(ब) अशनानि
(स) परीक्ष्य
(घ) कुर्यात्
उत्तर :
(स) परीक्ष्य
संस्कृतमाध्यमेन प्रश्नोत्तराणि –
एकपदेन उत्तरत (एक शब्द में उत्तर दीजिए)
प्रश्न 1.
देहं कथं विमृद्नीयात्?
(देह की कैसे मालिश करनी चाहिए ?)
उत्तरम् :
सुखम् (सुखपूर्वक)।
प्रश्न 2.
कीदृशं कर्म व्यायामसंज्ञितम् ?
(कैसा कर्म व्यायाम संज्ञक है ?)
उत्तरम् :
शरीरायासजननम् (शरीर को थकाने वाला)।

प्रश्न 3.
व्यायामेन गात्राणां का स्थितिः भवति ?
(व्यायाम से अंगों की क्या स्थिति होती है ?)
उत्तरम् :
सुविभक्तता (सम्यक् विभाजन)।
प्रश्न 4.
अग्नि: केन प्रदीप्तः भवति ?
(जठराग्नि किससे प्रदीप्त होती है ?)
उत्तरम् :
व्यायामेन (व्यायाम से)।
प्रश्न 5.
लाघवं केन भवति ?
(हलकापन किससे होता है ?)
उत्तरम् :
व्यायामेन (व्यायाम से)।
प्रश्न 6.
शीतोष्णसहिष्णुता कस्मात् उपजायते?
(सर्दी-गर्मी की सहन-क्षमता किससे होती है ?)
उत्तरम् :
व्यायामेन (व्यायाम से)।
प्रश्न 7.
व्यायामात् कीदृशम् आरोग्यम् उपजायते ?
(व्यायाम से कैसा आरोग्य पैदा होता है ?)
उत्तरम् :
परमम् (महान्)।

प्रश्न 8.
व्यायामेन शरीरे का परिणतिः भवति ?
(व्यायाम से शरीर में क्या परिवर्तन होता है ?)
उत्तरम् :
स्थौल्यापकर्षणम्
(मोटापा कम करना)।
प्रश्न 9.
व्यायामिनं केन अर्दयन्ति ?
(व्यायाम करने वाले को कौन नहीं पीड़ित करते ?)
उत्तरम् :
अरयः (शत्रु)।
प्रश्न 10.
उरगाः कस्मात् बिभ्यति ?
(साँप किससे डरते हैं ?)
उत्तरम् :
गरुडात् (गरुड़ से)।
प्रश्न 11.
बलिनां सदा पथ्यः कः ?
(बलवानों के लिए सदा पथ्य क्या है ?)
उत्तरम् :
व्यायामः।

प्रश्न 12.
पूर्णबलेन कृतः व्यायामः किं करोति?
(पूर्ण बल से किया व्यायाम क्या करता है ?)
उत्तरम् :
हन्ति (नष्ट कर देता है)।
प्रश्न 13.
हृदिस्थानं स्थितः वायुः कदा वक्त्रं प्रपद्यते ?
(हृदय में स्थित वायु कब मुँह तक पहुँचती है ?)
उत्तरम् :
बलार्द्धप्रयोगेन
(आधे बल के प्रयोग में)।
प्रश्न 14.
शरीरायासजननं किं कुर्यात् ?
(शरीर को थकाने के लिए क्या करना चाहिए?).
उत्तरम् :
व्यायामः (व्यायाम)।
प्रश्न 15.
देहं समन्ततः किं कुर्यात् ?
(शरीर का चारों ओर से क्या करना चाहिए ?)
उत्तरम् :
विमर्दनम् (मालिश)।
प्रश्न 16.
व्यायामेन कस्योपचयः भवति ?
(व्यायाम से किसकी वृद्धि होती है?)
उत्तरम् :
शरीरस्य (शरीर की)

प्रश्न 17.
व्यायामेन केषां सुविभक्तता भवति ?
(व्यायाम से किनका सुविभाजन होता है ?)
उत्तरम् :
गात्राणाम् (अंगों का)।
प्रश्न 18.
आरोग्य केनोपजायते ?
(आरोग्य किससे पैदा होता है ?)
उत्तरम् :
व्यायामेन (व्यायाम से)।
प्रश्न 19.
शीतादीनां व्यायामात् का उपजायते ?
(शीत आदि का व्यायाम से क्या पैदा होता है ?)
उत्तरम् :
सहिष्णुता (सहनशीलता)।
प्रश्न 20.
स्थौल्यापकर्षणं केन भवति ?
(मोटापा किससे दूर होता है ?)
उत्तरम् :
व्यायामेन (व्यायाम से)।

प्रश्न 21.
कं मनुष्यम् अरयः न अर्दयन्ति ?
(किस मनुष्य को शत्रु पीड़ित नहीं करते ?)
उत्तरम् :
व्यायामिनम्
(व्यायाम करने वाले को)।
प्रश्न 22.
जरा कं न समधिरोहति ?
(बुढ़ापा किसे नहीं घेरता ?)
उत्तरम् :
व्यायामिनम् (व्यायाम करने वाले को)।
प्रश्न 23.
व्यायामरतस्य किं स्थिरी भवति ?
(व्यायामरत का क्या स्थिर होता है ?)
उत्तरम् :
मासम्।
प्रश्न 24.
उगाः कं नोपसर्पन्ति ?
(साँप किसके पास नहीं जाते ?)
उत्तरम् :
वैनतेयस्य (गरुड़ के)।

प्रश्न 25.
व्यायामः वयोरूपगुणैीनमपि किं करोति ?
(व्यायाम आयु, रूप और गुणहीन को भी क्या करता है?)
उत्तरम् :
सुदर्शनम् (सुन्दर)।
प्रश्न 26.
किं कुर्वतः नित्यं विरुद्धमपि भोजनं परिपच्यते ?
(क्या करते हुए का विरुद्ध भोजन भी पचता है।)
उत्तरम् :
व्यायामम् (व्यायाम को)।
प्रश्न 27.
विरुद्धम् अपि भोजनं कस्य पचति ?
(विरुद्ध भोजन भी किसका पच जाता है ?)
उत्तरम् :
व्यायामिनः
(व्यायाम करने वाले का)।
प्रश्न 28.
कीदृशां बलिनां व्यायामः सदा पथ्यः ?
(कैसे बलवानों का व्यायाम सदा पथ्य है ?)
उत्तरम् :
स्निग्धभोजिनाम् (चिकना खाने वाले का)।

प्रश्न 29.
शीते वसन्ते च बलिनां व्यायामः कीदृशः स्मृतः ?।
(सर्दी और वसन्त में बलवानों का व्यायाम कैसा कहा गया है ?)
उत्तरम् :
पथ्यतमः (अधिक हितकर)।
प्रश्न 30.
कीदृशैः पुरुषैः व्यायामः करणीयः?
(कैसे मनुष्यों को व्यायाम करना चाहिए ?)
उत्तरम् :
आत्महितैषिभिः (अपना हित चाहने वालों को)।
प्रश्न 31.
कियत् बलेन व्यायामः करणीयः ?
(कितनी शक्ति से व्यायाम करना चाहिए ?)
उत्तरम् :
बलस्यार्द्धन (आधे बल से)।
प्रश्न 32.
वायुः कुत्र स्थितः भवति ?
(वायु कहाँ स्थित होती है ?)
उत्तरम् :
हृदिस्थाने (हृदय में)।

प्रश्न 33.
श्लोके कस्य लक्षणं कृतम् ?
(श्लोक में किसका लक्षण किया है ?)
उत्तरम् :
बलार्धस्य (आधे बल का)।
प्रश्न 34.
यः असमीक्ष्य व्यायामं करोति सः किं प्राप्नोति ?
(जो बिना सोचे-समझे व्यायाम करता है वह क्या प्राप्त करता
उत्तरम् :
रोगम् (बीमारी)।
प्रश्न 35.
अशनानि समीक्ष्य किं कुर्यात् ?
(भोजन की परख करके क्या करना चाहिए ?)
उत्तरम् :
व्यायामम्।
पूर्णवाक्येन उत्तरत –
(पूरे वाक्य में उत्तर दीजिए)
प्रश्न 36.
कीदृशं कर्म व्यायाम इति कथ्यते ?
(कैसा कर्म व्यायाम कहलाता है ?)
उत्तरम् :
शरीरायासजननं कर्म व्यायाम इति कथ्यते।
(शरीर थकाने वाला कर्म व्यायाम कहलाता है।)

प्रश्न 37.
व्यायामात् किम् उपजायते ?
(व्यायाम से क्या पैदा होता है?)
उत्तरम् :
व्यायामात् परमारोग्यमुपजायते।
(व्यायाम से महान् आरोग्य पैदा होता है।)
प्रश्न 38.
व्याधयः कमिव नोपसर्पन्ति व्यायामिनम् ?
(रोग किसकी तरह व्यायामी के पास नहीं आते ?)
उत्तरम् :
व्याघयः उरगाः इव नोपसर्पन्ति व्यायामिनम्।
(साँप की तरह रोग व्यायामी के पास नहीं आते)।
प्रश्न 39.
व्यायामः कं सुदर्शनं करोति ?
(व्यायाम किसको सुन्दर बनाता है ?)
उत्तरम् :
व्यायामः वयौरूपगुणै नमपि सुदर्शनं करोति।।
(व्यायाम आयु, रूप और गुणों से हीन व्यक्ति को भी सुन्दर बनाता है।)
प्रश्न 40.
केषां व्यायामः पथ्यः ?
(कैसों का व्यायाम पथ्य है ?)
उत्तरम् :
व्यायामः सदा बलिनां स्निग्धभोजिनां च पथ्यः।
(व्यायाम शक्तिशालियों और स्निग्ध भोजन करने वालों के लिए पथ्य है।)
प्रश्न 41.
व्यायामः कदा कं हन्ति ?
(व्यायाम कब और किसे मारता है ?)
उत्तरम् :
यः मनुष्यः पूर्णबलेन व्यायामं करोति तदा व्यायामः तं हन्ति।
(जो मनुष्य पूर्ण बल से जब व्यायाम करता है तब व्यायाम उसे नष्ट करता है।)

प्रश्न 42.
कस्य जन्तोः हृदि स्थितः वायुः वक्त्रं प्रवर्तते ?
(किस प्राणी के हृदय में स्थित वायु मुँह की ओर बढ़ती है ?)
उत्तरम् :
व्यायाम कुर्वतो जन्तोः हृदिस्थित: वायुः वक्त्रं प्रवर्तते।
(व्यायाम करते हुए प्राणी के हृदय में स्थित वायु मुख की ओर बढ़ती है।)
प्रश्न 43.
कति वस्तूनि समीक्ष्य व्यायाम कुर्यात् ?
(कितनी वस्तुओं को परखकर व्यायाम करना चाहिए ?)
उत्तरम् :
षड् वस्तूनि समीक्ष्य व्यायाम कुर्यात्।
(छः वस्तुएँ को परखकर व्यायाम करना चाहिए।)
प्रश्न 44.
पुरुषः रोगं कथं प्राप्नोति ? (मनुष्य रोग क्यों प्राप्त करता है ?)
उत्तरम् :
यः पुरुषः वयः आदि असमीक्ष्य व्यायामं करोति सः रोगम् आप्नोति।
(जो मनुष्य उम्र आदि का विचार किए बिना व्यायाम करता है वह रोग प्राप्त करता है।)
प्रश्न 45.
व्यायामं कृत्वा किं कुर्यात् ?
(व्यायाम करके क्या करना चाहिए ?)
उत्तरम् :
व्यायामं कृत्वा समन्ततः देहं सुखं विमृदूनीयात्।
(व्यायाम करके सभी ओर से शरीर की सुखपूर्वक मालिश करनी चाहिए।)

प्रश्न 46.
लाघवं केनोपजायते ?
(फुर्ती किससे होती है ?)
उत्तरम् :
व्यायामेन लाघवं जायते।
(व्यायाम से फुर्ती पैदा होती है।)
प्रश्न 47.
व्यायामेन केषां सहिष्णुतोपजायते ?
(व्यायाम से किसकी सहने की क्षमता होती है ?)
उत्तरम् :
व्यायामेन श्रमक्लमपिपासोष्ण-शीतादीनां सहिष्णुतोपजायते।
(व्यायाम से श्रम, थकावट, प्यास, गर्मी और सर्दी आदि की सहन क्षमता पैदा होती है।)
प्रश्न 48.
व्यायामेन सदृशं किञ्चित् अन्यत् कस्मात् न भवति ?
(व्यायाम के समान और कुछ क्यों नहीं होता ?)
उत्तरम् :
यत: व्यायामेन स्थौल्यापकर्षणं भवति।
(क्योंकि व्यायाम से मोटापा कम होता है।)
प्रश्न 49.
व्यायामिनं जरा कथं न समधिरोहति ?
(व्यायामी को बुढ़ापा कैसे नहीं घेरता ?)
उत्तरम् :
व्यायामिनं जरा सहसा आक्रम्य न समधिगच्छति।।
(व्यायामी को बुढ़ापा अचानक आक्रमण करके नहीं घेरता है।)
प्रश्न 50.
व्याधयः कस्य समीपं नोपसर्पन्ति ?
(व्याधियाँ किसके समीप नहीं आती ?)
उत्तरम् :
व्याधयः व्यायामस्विन्नगात्रस्य पद्भ्यामुवर्तितस्य च नोपसर्पन्ति।
(व्याधियाँ व्यायाम के कारण पसीने से भीगे और पैरों से मर्दित के पास नहीं आती।)

प्रश्न 51.
व्यायाम कुर्वतः भोजनं कथं परिपच्यते ?
(व्यायाम करते हुए का भोजन कैसे पचता है ?)
उत्तरम् :
व्यायाम कुर्वतः भोजनं निर्दोषं परिपच्यते।
(व्यायाम करने वाले का भोजन बिना दोष के पच जाता है।)
प्रश्न 52.
बलिनां व्यायामः कदा पथ्यतमः स्मृतः ?
(बलियों का व्यायाम कब हितकर अथवा लाभकारी कहा गया
उत्तरम् :
बलिनां व्यायामः शीते वसन्ते च पथ्यतमः स्मृतः।
(बलियों का व्यायाम सर्दी और वसन्त में पथ्यतम होता है।)
प्रश्न 53.
आत्महितैषिभिः व्यायामः कदा करणीयः ?
(अपना हित चाहने वालों को व्यायाम कब करना चाहिए ?)
उत्तरम् :
आत्महितैषिभिः पुरुषैः सर्वेषु ऋतुषु प्रतिदिनं व्यायामः करणीयः।
(अपना हित चाहने वाले पुरुषों को सभी ऋतुओं में प्रतिदिन व्यायाम करना चाहिए।)

प्रश्न 54.
कानि समीक्ष्य व्यायाम कुर्यात् ? (क्या परखकर व्यायाम करना चाहिए ?)
उत्तरम् :
वयोबलशरीराणि देशकाल-अशनानि च समीक्ष्य व्यायाम कुर्यात्।।
(आयु-बल-शरीर-देश-काल और भोजन की समीक्षा करके व्यायाम करना चाहिए।)
अन्वय-लेखनम –
अधोलिखितश्लोकस्यान्वयमाश्रित्य रिक्तस्थानानि मञ्जूषातः समुचितपदानि चित्वा पूरयत।
(नीचे लिखे श्लोक के अन्वय के आधार पर रिक्तस्थानों की उचित पद चुनकर कीजिए।)
1. शरीरायासजननं …………………………… विमृद्नीयात् समन्ततः।।
मञ्जूषा – समन्ततः, संज्ञितम्, कर्म, देहं।
शरीर-आयास-जननं (i) …………. व्यायाम-(i) ……………., तत् कृत्वा तु (iii) …………… सुखं (iv) ………….. विमृद्नीयात्।
उत्तरम् :
(i) कर्म (ii) संज्ञितम् (iii) देहं (iv) समन्ततः।
2. शरीरोपचयः कान्तिर्गात्राणां ………………………. स्थिरत्वं लाघवं मृजा।।
मञ्जूषा – अनालस्यं, कान्तिः, शरीरोपचयः, लाघवं।
सुविभक्तता (i) ……………… गात्राणां (ii) ……………… दीप्ताग्नित्वम् (iii) ………………. स्थिरत्वं (iv) …………….. मृजा।
उत्तरम् :
(i) शरीरोपचयः (ii) कान्तिः (iii) अनालस्यं (iv) लाघवं।

3. श्रमक्लमपिपासोष्ण-शीतादीनां ……………………. व्यायामादुपजायते।।
मञ्जूषा – अपि, शीतादीनां, क्लम, परमं।
श्रम (i) …………………, पिपासा, उष्ण, (ii) ………………. सहिष्णुता (iii) ……………… च आरोग्यम् (iv) ……………… व्यायामादुपजायते।
उत्तरम् :
(i) क्लम (ii) शीतादीनां (iii) परमं (iv) अपि।
4. न चास्ति सदृशं तेन …………………………….. मर्त्यमर्दयन्त्यरयो बलात्।।
मञ्जूषा – मर्त्यम्, सदृशं, अर्दयन्ति, अपकर्षम्।
तेन च (i) ……………….. किञ्चित् स्थौल्य-(ii) …………… नास्ति व्यायामिनं (iii) ……………… अरयः बलात् न (iv) ……………… च।
उत्तरम् :
(i) सदृशं (ii) अपकर्षम् (iii) मर्त्यम् (iv) अर्दयन्ति।
5. न चैनं सहसाक्रम्य ………………… व्यायामाभिरतस्य च।।
मञ्जूषा – सहसा, स्थिरी, च, समधिरोहति।
च एनं (i) ………………. आक्रम्य जरा न (ii) ……………….. व्यायामाभिरतस्य (iii) ……………… मांसं (iv) ………….. भवति।
उत्तरम् :
(i) सहसा (ii) समधिरोहति (iii) च (iv) स्थिरी।
6. व्यायामस्विन्नगात्रस्य ……………………… कुर्यात्सुदर्शनम्।।
मञ्जूषा – सुदर्शनं, इव, पद्भ्यामुवर्तितस्य, नोपसर्पन्ति।
व्यायामस्विन्नगात्रस्य च (i) ………………. वैनतेयम् उरगाः (ii) ……………….. व्याधयो (iii) …………………। वयोरूपगुणहीनमपि (iv) ………………… कुर्यात्।
उत्तरम् :
(i) पद्भ्यामुवर्तितस्य (ii) इव (iii) नोपसर्पन्ति (iv) सुदर्शन।

7. व्यायाम कुर्वता …………………………… निर्दोषं परिपच्यते।।
मञ्जूषा – व्यायाम, निर्दोष, अविदग्धम्, विरुद्धम्।
नित्यं (i) ……………….. कुर्वतो भोजनं (ii) ……………… अपि विदग्धम् (iii) ……………….. वा (iii)……. परिपच्यते।
उत्तरम् :
(i) व्यायाम (ii) विरुद्धम् (iii) अविदग्धम् (iv) निर्दोषं।
8. व्यायामो हि सदा ……………………………………………. पथ्यतमः स्मृतः।।
मञ्जूषा – पथ्यतमः पथ्यः, बलिनां, शीते।
स्निग्धभोजिनाम् (i)……. व्यायामो हि सदा (ii)……. सः च तेषां (iii)……. वसन्ते च (iv)……. स्मृतः।
उत्तरम् :
(i) बलिनां (ii) पथ्यः (iii) शीते (iv) पथ्यतमः
9. सर्वेष्वृतुष्वहरहः ………………………………………………. हन्त्यतोऽन्यथा।।
मञ्जूषा-कर्त्तव्यः, बलस्यार्थेन, अहरहः, अन्यथा।
सर्वेषु ऋतुषु (i)…… पुम्भिः आत्महितैषिभिः, (ii)….. व्यायामः (i)….. अत: (iii)……, (व्यायाम:) हन्ति।
उत्तरम् :
(i) अहरहः (ii) बलस्यार्धेन (iii) कर्त्तव्यः (iv) अन्यथा।
10. हृदिस्थानास्थितो वायुर्यदा ……………………………………… लक्षणम्।।
मञ्जूषा – व्यायामकुर्वतः, प्रपद्यते, बलार्धस्य, हृदिस्थानास्थितो। यदा (i)……. वायुः वक्त्रं (ii)……. तद् (iii)……. जन्तोः (iii)……. लक्षणम्।
उत्तरम् :
(i) हृदिस्थानास्थितो (ii) प्रपद्यते (iii) व्यायामकुर्वतः (iv) बलार्धस्य।

11. वयोबलशरीराणि ……………………………. रोगमाप्नुयात्।।
मञ्जूषा – शरीराणि, अन्यथा, व्यायाम, अशनानि।
वय:-बल-(i)……. च देश-काल-(ii)……. समीक्ष्य (iii)……. कुर्यात् (iii)…….रोगमाप्नुयात्।
उत्तरम् :
(i) शरीराणि (ii) अशनानि (iii) व्यायाम (iv) अन्यथा।
प्रश्ननिर्माणम् –
अधोलिखित वाक्येषु स्थूलपदमाधृत्य प्रश्ननिर्माणं कुरुत –
1. शरीरायासजननं कर्म व्यायामसंज्ञितम्।
(शरीर के श्रम से उत्पन्न कर्म व्यायाम संज्ञक है।)
2. व्यायामं कृत्वा सुखेन देहं समन्ततः विमृद्नीयात्।।
(व्यायाम करके सुखपूर्वक देह का सभी ओर से मर्दन करना चाहिए।)
3. व्यायामिनं मर्त्यम् अरयः बलात् न अर्दयन्ति।
(व्यायामी मनुष्य को शत्रु बलपूर्वक नहीं कुचल डालते हैं।)
4. व्यायामिनं सहसाक्रम्य जरा न समधिरोहति।
(व्यायामी व्यक्ति को अचानक आक्रमण करके बुढ़ापा आरूढ़ नहीं होता।)
5. व्यायामरतस्य मांसं स्थिरीभवति।
(व्यायामरत (मनुष्य) का मांस स्थिर रहता है।)
6. व्यायामस्विन्नगात्रस्य व्याधयो नोपसर्पन्ति।
(व्यायाम के कारण पसीने से लथपथ शरीर वालों के व्याधियाँ पास नहीं आती।)
7. वैनतेयम् उरगाः नोपसर्पन्ति ?
(गरुड़ के पास सर्प नहीं आते हैं।)
8. व्यायाम कुर्वतः विरुद्धमपि भोजनं निर्दोषं परिपच्यते।
(व्यायाम करते हुए व्यक्ति को विरुद्ध भोजन भी निर्दोष पचता है।)
9. व्यायामो हि सदा पथ्यो बलिनां स्निग्धभोजिनाम्।
(बलवान् और स्नेहयुक्त भोजन करने वालों के लिए व्यायाम सदा पथ्य होता है।)
10. आरोग्यम् चापि व्यायामाद् उजायते।
(आरोग्य आदि व्यायाम से प्राप्त होते है।)
उत्तराणि :
1. कीदृशं कर्म व्यायामसंज्ञितम् ?
2. किं कृत्वा सुखं देहं समन्ततः विमृद्नीयात् ?
3. कं मर्त्यम् अरयः बलात् न अर्दयन्ति ?
4. व्यायामिनं सहसाक्रम्य का न समधिरोहति ?
5. कस्य मांसं स्थिरी भवति ?
6. कस्य व्याधयः नोपसर्पन्ति ?
7. कम् उरगाः नोपसर्पन्ति ?
8. कस्य विरुद्धमपि भोजनं निर्दोषं परिपच्यते ?
9. व्यायामो हि सदा कस्य पथ्यः ?
10. आरोग्यम् चापि कस्मात् उपजायते?

भावार्थ-लेखनम् –
अधोलिखित पद्यांशानां संस्कृते भावार्थं लिखत –
1. शरीरायासजननं कर्म ………………………….. विमृद्नीयात् समन्ततः ॥
भावार्थ – वपुसः उद्यमेन या श्रान्ति भवति तत् कर्म व्यायाम इति नाम्ना ज्ञायते। तत्कर्म व्यायाम वा विधाय तु मानवस्य शरीरं सुखी भवति। व्यायामं कृत्वा सर्वतः शरीरस्य अभ्यजनं कुर्यात्।
2. शरीरोपचयः ……………………. लाघवं मृजा ॥
भावार्थ – अनेन व्यायामेन मानवशरीरस्य सुविभक्तता शारीरिक सौष्ठवम् वा, अङ्गानां विकास: जठराग्ने: प्रवर्धने, आलस्य प्रमाद हीनता वा स्थैर्यम् शरीरे स्फूर्तिः स्वच्छीकरणं च भवति।
3. श्रमक्लमपिपासोष्ण-शीतादीनां …………………….. व्यायामादुपजायते ॥
भावार्थ – श्रमजनित शैथिल्यं, जलपातुमिच्छा, तापः, शैत्यादीनां सो, क्षमता सामर्थ्य वा अत्यधिकं नैरोग्यं अपि व्यायामात् सम्भवति।

4. न चास्ति सदृशं तेन ………………………… मर्त्यमर्दयन्त्यरयो बलात् ॥
भावार्थ – अमुना (व्यायामेन) तुल्यं किमपि नास्ति यः स्थूलतां पीवरतां वा दूरीकर्तुं शक्नोति। अर्थात् व्यायामात् पीनत्वं दूरीकरणं तनुता सम्भवति। श्रमरतं मानवं शत्रवोऽपि बलपूर्वकं न पीडयन्ति।
5. न चैनं सहसाक्रम्य …………………….. व्यायामाभिरतस्य च ॥
भावार्थ – च इमं व्यायामिनं अकस्मादेव वार्धक्यमपि आरूढं न भवति। परिश्रमे संलग्नस्य पिशितमपि शान्तं जायते।
6. व्यायामस्विन्नगात्रस्य ……………………………………. कुर्यात्सुदर्शनम् ॥
भावार्थ – परिश्रमजनित श्रम जलेन क्लिन्न शरीरस्य पादाभ्यां च उन्नमितस्य समीपे व्याधय रोगाः वा न आयान्ति। यथा गरुडस्य समीपे सर्पाः न आयान्ति। सौन्दर्यरहितं गुणविशेष रहितमपि व्यायामः सुदर्शनीयं करोति।
7. व्यायाम कुर्वतो नित्यं …………………………………. निर्दोषं परिपच्यते ॥
भावार्थ – यः मनुष्य सदैव प्रतिदिनं उद्यमं करोति तस्य प्रतिकूलम् अपि, सुपक्वम् अपक्वम् वापि भोजनं दोषं विनैव पचति।
8. व्यायामो हि सदा पथ्यो …………………….. तेषां पथ्यतमः स्मृतः ॥
भावार्थ-तैलघृतादि स्नेहयुक्त अशनानि भुञ्जानानां शक्तिशालिनां परिश्रमः सर्वदा सर्वाधिक हितकरः कथ्यते।

शेमुषी-द्वितीयो भागः
9. सर्वेष्वृतुष्वहरहः ………………………………………. व्यायामो हन्त्यतोऽन्यथा ॥
संस्कृत व्याख्या: – अखिलेषु कालेषु प्रतिदिनं स्वकीयं हिताभिलाषुकैः पुरुषैः आत्मनः शरीरस्य शक्तेः अर्धांशेन एव परिश्रमः करणीयः। अस्मात् अधिक: व्यायामः मानवं नाशयति। पूर्ण सामर्थ्येन विहितः व्यायामः व्याधिमामन्ययति।
10. हृदिस्थानास्थितो …………………………………………. लक्षणम् ॥
भावार्थ – यस्मिन् काले हृदयस्थले विद्यमानः वातः मुखं प्रवर्तते तत् व्यायामिनः प्राणिनः अर्ध बलस्य सङ्केत भवति।
11. वयोबलशरीराणि ……………………………… रोगमाप्नुयात् ॥
भावार्थ – आयुः बलं (शक्ति) गात्राणि, स्थानं समयं भोजनं च सम्यक् परीक्ष्य एव परिश्रमं (व्यायाम) कुर्वीत् नोचेत् रुग्णताम् आप्नोति।
अधोलिखितसूक्तीनां भावबोधं हिन्दी-अंग्रेजी-संस्कृतभाषया वा लिखत।
(निम्नलिखित सूक्तियों का भावार्थ हिन्दी, अंग्रेजी अथवा संस्कृत भाषा में लिखिए।)
(i) शरीरायासजननं कर्म व्यायामसंज्ञितम्।
भावार्थ – येन कार्येण श्रान्तिः श्रमं वा भवति तत् कर्म व्यायाम इति नाम्ना ज्ञायते।
(जिस कार्य से थकावट अथवा श्रम होता है वह काम व्यायाम के नाम से जाना जाता है।)

(ii) आरोग्यं चापि परमं व्यायामादुपजायते।
भावार्थ – व्यायामः तु नीरोगतां स्वस्थतां वा अपि करोति।
(व्यायाम तो रोगरहित अथवा स्वस्थ भी करता है।)
(iii) न चास्ति सदृशं तेन किञ्चित्स्थौल्यापकर्षणम्।
भावार्थ – अतः व्यायामेन तुल्यः न अन्यत् किञ्चित् कार्यं यत् शरीरस्य स्थूलतां गुरुतां वा अपकर्षेत्।
(अतः व्यायाम के समान अन्य कोई कार्य नहीं जो शरीर का मोटापा दूर करे।)
(iv) व्यायामो हि सदा पथ्यः।
भावार्थ – व्यायामः श्रमः वा सदैव मानवस्य हितकारकः भवति।
(व्यायाम अथवा श्रम सदैव मानव का हितकारक होता है।)
(v) बलस्यार्धन कर्तव्यो व्यायामः।
भावार्थ – मानवेन स्वस्य अर्द्धसामर्थ्येन व्यायामः करणीयः न तु पूर्ण बलेन।
(मनुष्य को अपनी आधी क्षमता से ही व्यायाम करना चाहिए न कि पूरे बल से।)
व्यायामः सर्वदा पथ्यः Summary and Translation in Hindi
पाठ-परिचय – संस्कृत में आयुर्विज्ञान विषय पर प्रभूत साहित्य की रचना हुई है। इसी क्रम में तीसरी शताब्दी में आचार्य सुश्रुत ने ‘सुश्रुतसंहिता’ की रचना की। ‘सुश्रुतसंहिता’ में शल्य-चिकित्सा की प्रधानता है। इस ग्रन्थ में रोगों की चिकित्सा के साथ-साथ उनके पथ्यों का भी उल्लेख किया गया है। ‘सुश्रुतसंहिता’ छः खण्डों में विभक्त है, जिन्हें ‘स्थान’ कहा गया है।
प्रस्तुत पाठ आयुर्वेद के इसी प्रसिद्ध ग्रन्थ के चिकित्सास्थान के 24वें अध्याय से संकलित है। इसमें आचार्य सुश्रुत ने व्यायाम की परिभाषा बताते हुए उससे होने वाले लाभों की चर्चा की है। शरीर में सुगठन, कान्ति, स्फूर्ति, सहिष्णुता, नीरोगता आदि व्यायाम के प्रमुख लाभ हैं।

मूलपाठः, अन्वयः, शब्दार्थाः, सप्रसंग हिन्दी-अनुवादः
1. शरीरायासजननं कर्म व्यायामसंज्ञितम्।
तत्कृत्वा तु सुखं देहं विमृद्नीयात् समन्ततः ।।1।।
अन्वयः – शरीर-आयास-जननं कर्म व्यायाम-संज्ञितम्, तत् कृत्वा तु देहं सुखं समन्ततः विमृद्नीयात्।
शब्दार्थाः – शरीर = गात्रे (शरीर में), आयास = श्रमम् (थकावट), जननम् = उत्पादकम् (पैदा करने वाला), कर्म = कार्यम् (कार्य), व्यायाम = (कसरत), संज्ञितम् = नामधेयम् (नामवाला है), तत् = तं व्यायामम् (उस व्यायाम को), कृत्वा = सम्पाद्य, विधाय (करके), तु = तदा (तब), देहम् = गात्रम् (शरीर को), सखम् = सुखपूर्वकम, सहजभावेन (सुखपूर्वक), समन्ततः = सर्वतः (पूरी तरह से, सभी ओर से), विमृदुनीयात् = मर्दयेत् (मालिश करनी चाहिए।
सन्दर्भ-प्रसङ्गश्च – यह श्लोक हमारी शेमुषी पाठ्यपुस्तक के ‘व्यायामः सर्वदा पथ्यः’ पाठ से उद्धृत है। यह पाठ आचार्य सुश्रुत रचित ‘सुश्रुत-संहिता’ से सङ्कलित है। इस श्लोक में आचार्य व्यायाम की परिभाषा प्रस्तुत करते हैं। वे कहते हैं –
हिन्दी-अनुवादः – शरीर में थकावट पैदा करने वाला कार्य व्यायाम नाम वाला है अर्थात् व्यायाम कहलाता है। उस व्यायाम को करके तो (तब) सुखपूर्वक (सहज रूप से) पूरी तरह (सभी ओर से शरीर के अंगों की) मालिश करनी चाहिए।

2. शरीरोपचयः कान्तिर्गात्राणां सुविभक्तता।
दीप्ताग्नित्वमनालस्यं स्थिरत्वं लाघवं मृजा ।।2।।
अन्वयः – सुविभक्तता शरीरोपचयः गात्राणां कान्तिः दीप्ताग्नित्वम् अनालस्यं स्थिरत्वं लाघवं मृजा।
शब्दार्थाः – (व्यायामेन) सुविभक्तता = शारीरिकं सौष्ठवम् (शारीरिक सौन्दर्य), (सम्यक विभक्तस्य) शरीरोपचयः = गात्रस्य अभिवृद्धिः, अंगानां विकासः (शरीर की वृद्धि), गात्राणाम् = अङ्गानाम् (अंगों की), कान्तिः = आभा (चमक), दीप्ताग्नित्वम् = जठराग्नेः प्रवर्धनम् (जठराग्नि का प्रदीप्त होना अर्थात् भूख लगना), अनालस्यम् = आलस्यहीनता (आलस्यहीनता), स्थिरत्वम् = स्थिरता (स्थिरता), लाघवं = स्फूर्तिः (फुर्ती), मृजा = स्वच्छीकरणम् (स्वच्छता), (भवन्ति = होती हैं)।।
सन्दर्भ – प्रसङ्गश्च – यह श्लोक हमारी ‘शेमुषी’ पाठ्य पुस्तक के ‘व्यायामः सर्वदा पथ्यः’ पाठ से लिया गया है। यह पाठ आचार्य सुश्रुत द्वारा रचे गये ग्रन्थ ‘सुश्रुत संहिता’ से संकलित है। इस श्लोक में आचार्य व्यायाम के लाभों को बताकर उसका महत्व प्रदर्शित करते हैं।
हिन्दी-अनुवादः – (व्यायाम से) शारीरिक सौन्दर्य, शरीर की वृद्धि, अंगों की चमक, जठराग्नि का प्रदीप्त होना अर्थात् भूख लगना, आलस्यहीनता, स्थिरता, फुर्ती एवं स्वच्छता (होती हैं)।
3. श्रमक्लमपिपासोष्ण-शीतादीनां सहिष्णुता।।
आरोग्यं चापि परमं व्यायामादुपजायते ।।3।।
अन्वयः – श्रम क्लम, पिपासा, उष्ण, शीतादीनां सहिष्णुता परमं च आरोग्यम् अपि व्यायामादुपजायते।
शब्दार्थाः – श्रमक्लमः = श्रमजनितं शैथिल्यम् (थकान), पिपासा = पातुम् इच्छा (प्यास), उष्णः = तापः (गर्मी), शीतादीनाम् = शैत्यादीनाम् (ठण्ड आदि की), सहिष्णुता = सहत्वं/सोढुं क्षमता (सहन करने की शक्ति/सामर्थ्य), च = (और), परमम् = अत्यधिकम् (महान्), आरोग्यम् अपि = स्वस्थता/नीरोगिता अपि (रोगहीनता भी), व्यायामाद् = श्रमाद् (कसरत करने से), उपजायते = सम्भवति (होता है)।
सन्दर्भ-प्रसङ्गश्च – यह श्लोक हमारी पाठ्य पुस्तक शेमुषी के ‘व्यायाम सर्वदा पथ्यः’ पाठ से उद्धृत है। यह पाठ आचार्य सुश्रुत रचित ‘सुश्रुत संहिता’ ग्रन्थ से संकलित है। इस श्लोक में आचार्य व्यायाम से होने वाले गुणों का प्रतिपादन करते हुए कहते हैं।
हिन्दी-अनुवादः – थकान, प्यास, गर्मी, ठण्ड आदि को सहन करने की शक्ति और महान् स्वस्थता (नीरोगता) अर्थात् रोग-हीनता व्यायाम से होती है।

4. न चास्ति सदृशं तेन किञ्चित्स्थौल्यापकर्षणम्।
न च व्यायामिनं मर्त्यमर्दयन्त्यरयो बलात् ।।4।।
अन्वयः – तेन च सदशं किञ्चित स्थौल्य-अपकर्षम नास्ति व्यायामिनं मर्त्यम अरयः बलात न अर्दयन्ति च।
शब्दार्थाः – तेन च = अमुना च (और इसके), सदृशं = समानं, तुल्यम् (समान), किञ्चित् = (कुछ), स्थौल्यापकर्षणम् = अतिमांसलत्वम्, पीनताम् दूरीकरणम् (मोटापा दूर करना, कम करना), नास्ति = न वर्तते (नहीं है), व्यायामिनम् = श्रमरतं, व्यायामनिरतम् (व्यायाम करने वाले व्यक्ति को), मर्त्यम् = मनुष्यम् (मानव को), अरयः = शत्रवः (शत्रुगण), बलात् = बलपूर्वकम् (जबरदस्ती), न अर्दयन्ति = अर्दनं न कुर्वन्ति, न पीडयन्ति (नहीं कुचल डालते हैं)।
सन्दर्भ-प्रसङ्गश्च – प्रस्तुत श्लोक हमारी संस्कृत की पाठ्यपुस्तक ‘शेमुषी’ (द्वितीयो भागः) के ‘व्यायामः सर्वदा पथ्यः’ शीर्षक पाठ से उद्धृत किया गया है। मूलतः यह पाठ आचार्य सुश्रुत द्वारा विरचित आयुर्वेद के सुप्रसिद्ध ग्रन्थ ‘सुश्रुतसंहिता’ के चिकित्सास्थान में वर्णन किये गये 24वें अध्याय से संकलित किया गया है। इस श्लोक में व्यायाम करने से मोटापा दूर किये जाने का लाभ वर्णित करते हुए कहा गया है कि व्यायाम करने वाले को शत्रु भी पराजित नहीं कर पाते हैं।
हिन्दी-अनुवादः – और उस व्यायाम के समान मोटापा दूर (कम) करने वाला कोई (साधन) नहीं है। व्यायाम करने वाले व्यक्ति को शत्रुगण जबर्दस्ती नहीं कुचल सकते हैं। (या पीड़ा नहीं देते।)

5. न चैनं सहसाक्रम्य जरा समधिरोहति।
स्थिरीभवति मांसं च व्यायामाभिरतस्य च।। 5।।
अन्वयः – च एनं सहसा आक्रम्य जरा न समधिरोहति व्यायामाभिरतस्य च मांसं स्थिरी भवति।
शब्दार्थाः – च एनम् = च इमं व्यायामिनम् (और इस व्यायाम करने वाले को), सहसा = अकस्मात् (अचानक), जरा = वृद्धत्वं, वार्धक्यम् (बुढ़ापा), न समधिरोहति = न आरूढं भवति (सवार नहीं होता है, नहीं दबोचता), व्यायामाभिरतस्य च = व्यायामे/परिश्रमे संलग्नस्य च (और व्यायाम/परिश्रम में संलग्न/लगे हुए व्यक्ति का), मांसं = आमिषम्, पिशितम् (मांस), स्थिरी = शान्तः (स्थिर), भवति = जायते (होता है)।
सन्दर्भ-प्रसङ्गश्च – यह श्लोक हमारी शेमुषी पाठ्य पुस्तक के ‘व्यायाम सर्वदा पथ्यः’ पाठ से लिया गया है। यह पाठ आचार्य सुश्रुत-विरचित ‘सुश्रुत संहिता’ आयुर्वेद ग्रन्थ से सङ्कलित है। इस श्लोक में आचार्य सुश्रुत कहते हैं कि व्यायाम करने वाले व्यक्ति का मांस स्थिर हो जाता है तथा उसे अकस्मात् बुढ़ापा भी नहीं घेरता है।
हिन्दी-अनुवादः- और इस व्यायाम (परिश्रम) करने वाले को बुढ़ापा अचानक नहीं दबोचता (आरूढ़ होता) है। व्यायाम (परिश्रम) में संलग्न (लगे हुए) व्यक्ति का मांस स्थिर (शान्त) रहता है।
6. व्यायामस्विन्नगात्रस्य पद्भ्यामुवर्तितस्य च।
व्याधयो नोपसर्पन्ति वैनतेयमिवोरगाः
वयोरूपगुणैीनमपि कुर्यात्सुदर्शनम्।।6।।
अन्वयः – व्यायामस्विन्नगात्रस्य च पद्भ्यामुवर्तितस्य वैनतेयम् उरगाः इव व्याधयो नोपसर्पन्ति। वयोरूपगुणहीनमपि सुदर्शनं कुर्यात्।
शब्दार्थाः – व्यायाम = व्यायामेन, परिश्रमेण (व्यायाम या परिश्रम से), स्विन्नगात्रस्य = श्रमजलेन, स्वेदेन सिक्तस्य शरीरस्य (पसीने से लथपथ शरीर वाले का), च पद्भ्याम् = च पादाभ्याम् (और पैरों से), उद्वर्तितस्य = उन्नमितस्य (ऊपर उठने वाले, पैरों से रौंधने वाले, व्यायाम करने वाले के), वैनतेयम् = गरुड़ (गरुड़ के), उरगाः इव = सर्पाः इव (साँपों के समान) व्याधयः = रोगाः (बीमारियाँ), नोपसर्पन्ति = समीपं न आयान्ति (पास नहीं आती हैं), वयो = आयुसं (आयु), रूप = सौन्दर्य (सुन्दर रूप), गुण = गुण विशेष (गुण विशेष), हीनम् अपि = रहितमपि (रहित को भी). सुदर्शनम् = शोभनीयं (सुन्दर दिखाई देने वाला), कुर्यात् = करोति (बना देता है)।
सन्दर्भ-प्रसङ्गश्च – प्रस्तुत श्लोक हमारी संस्कृत की पाठ्यपुस्तक ‘शेमुषी’ के ‘व्यायामः सर्वदा पथ्यः’ शीर्षक पाठ से उद्धृत किया गया है। मूलतः यह पाठ आचार्य सुश्रुत द्वारा विरचित आयुर्वेद के सुप्रसिद्ध ग्रन्थ ‘सुश्रुतसंहिता’ के चिकित्सास्थान में वर्णन किये गये 24वें अध्याय से संकलित किया गया है। इस श्लोक में व्यायाम के महत्त्व को प्रदर्शित करते हुए कहा गया है कि व्यायाम करने वाला कभी रोगी नहीं बनता है।
हिन्दी-अनुवादः- व्यायाम या परिश्रम के कारण पसीने से लथपथ शरीर वाले तथा पैरों से रौंधे हुए शरीर वाले व्यक्ति के पास व्याधियाँ गरुड़ के पास साँपों की तरह नहीं आती हैं। (व्यायाम) आयु, रूप और गुणरहित व्यक्ति को भी दर्शनीय बना देता है।

7 व्यायाम कुर्वतो नित्यं विरुद्धमपि भोजनम्।
विदग्धमविदग्धं वा निर्दोषं परिपच्यते ।।7।।
अन्वयः – नित्यं व्यायामं कुर्वतो भोजनं विरुद्धम् अपि विदग्धम् अविदग्धम् वा निर्दोषं परिपच्यते।।
शब्दार्थाः – नित्यम् = सदैव, प्रतिदिनम् (हमेशा, रोजाना), व्यायामम् = श्रमम् (व्यायाम), कुर्वतः = कुर्वाणस्य (करने वाले के), भोजनम् = खाद्यम्, अशनम् (भोजन के), विरुद्धम् = प्रतिकूलम् (विपरीत होने पर भी), वा = अथवा (भोजनम् = खाना), विदग्धम् = सुपक्वम् (भली-भाँति पका हुआ), अविदग्धम् = अपक्वम् (न पका हुआ), निर्दोषं = दोषं विना (बिना किसी दोष के), परिपच्यते = जीर्यते (आसानी से पच जाता है)।
सन्दर्भ-प्रसङ्गश्च – यह श्लोक हमारी शेमुषी पाठ्य पुस्तक के व्यायामः सर्वदा पथ्यः पाठ से लिया गया है। यह पाठ आचार्य सुश्रुत-रचित सुश्रुत-संहिता आयुर्वेद ग्रन्थ से सङ्कलित है। इस श्लोक में आचार्य प्रतिपादित करते हैं कि व्यायाम से सब प्रकार का भोजन अच्छी तरह पचता है।
हिन्दी-अनुवादः – रोजाना व्यायाम करने वाले मनुष्य को विपरीत होते हुए भी भली-भाँति पके हुए तथा कम पके हुए भोजन आसानी से बिना परेशानी के पच जाते हैं।
8 व्यायामो हि सदा पथ्यो बलिनां स्निग्धभोजिनाम्।
स च शीते वसन्ते च तेषां पथ्यतमः स्मृतः।।8।।
अन्वयः – स्निग्धभोजिनाम् बलिनां व्यायामो हि सदा पथ्यः सः च तेषां शीते वसन्ते च पथ्यतमः स्मृतः।
शब्दार्थाः – स्निग्धभोजिनाम् = स्नेहयुक्त अशनानि खादताम् (चिकना भोजन खाने वालों), बलिनाम् = बलवताम्, शक्तिशालिनाम् (बलवान् व्यक्तियों के लिए), व्यायामो हि = व्यायामः, परिश्रमः (व्यायाम), सदा = सर्वदा (हमेशा), पथ्यतमः = सर्वाधिकः हितकरः (सबसे अधिक हितकर), स्मृतः = कथ्यते (कहा जाता है)। . सन्दर्भ-प्रसङ्गश्च-यह श्लोक हमारी शेमुषी पाठ्यपुस्तक के व्यायामः सर्वदा पथ्यः पाठ से लिया गया है। यह पाठ आचार्य सुश्रुत-रचित सुश्रुत-संहिता आयुर्वेद ग्रन्थ से सङ्कलित है। इस श्लोक में आचार्य व्यायाम का उचित काल बताते हैं। शीतकाल और बसन्त काल में व्यायाम करना सबसे अधिक लाभदायक होता है।
हिन्दी-अनुवादः – चिकना भोजन खाने वालों और बलवान् व्यक्तियों का व्यायाम शीत और वसंत में सदैव सबसे . अधिक हितकर कहलाता है।

9. सर्वेष्वृतुष्वहरहः पुम्भिरात्महितैषिभिः।
बलस्यार्धेन कर्त्तव्यो व्यायामो हन्त्यतोऽन्यथा।।9।।
अन्वयः – सर्वेषु ऋतुषु अहरहः पुम्भिः आत्महितैषिभिः, बलस्यार्धेन व्यायामः कर्त्तव्यः अतः अन्यथा, (व्यायामः) हन्ति।
शब्दार्थाः – सर्वेषु = अखिलेषु (सभी), ऋतुषु = कालेषु (ऋतुओं में), अहरहः = प्रतिदिनम् (हर रोज), पुम्भिः = पुरुषैः (मनुष्यों द्वारा, मनुष्यों को), आत्महितैषिभिः = स्वकीयं हितं आत्मनः हितं अभिलाषुकैः (अपना हित चाहने वालों द्वारा, या अपना हित चाहने वालों को), (आत्मनः शरीरस्य = अपने शरीर के), बलस्यार्धेन = अर्द्ध बलेन, शक्तेः अर्धांशेन (आधे बल से ही), व्यायामः कर्तव्यः = परिश्रमः करणीयः (व्यायाम करना चाहिए), अतोऽन्यथा = अस्मात् अधिकतरः व्यायामः (इससे अधिक व्यायाम मनुष्य को), हन्ति = मारयति, नाशयति (मार देता है)।
सन्दर्भ-प्रसङ्गश्च – यह श्लोक हमारी शेमुषी पाठ्य पुस्तक के ‘व्यायामः सर्वदा पथ्यः’ पाठ से लिया गया है। यह पाठ आचार्य सुश्रुत-रचित सुश्रुत-संहिता आयुर्वेद ग्रन्थ से सङ्कलित है। इस श्लोक में आचार्य व्यायाम की मात्रा का वर्णन करते। कहते हैं कि अपना भला चाहने वालों द्वारा व्यायाम आधे बल से ही करना चाहिए अन्यथा हानिकारक होता है।
हिन्दी-अनुवादः – सभी ऋतुओं में हर रोज अपने हित के अभिलाषी (चाहने वाले) मनुष्यों को अपने शरीर के आधे बल से व्यायाम करना चाहिए। इससे अधिक व्यायाम मनुष्य को मार देता है।
10. हृदिस्थानास्थितो वायुर्यदा वक्त्रं प्रपद्यते।
व्यायाम कुर्वतो जन्तोस्तबलार्धस्य लक्षणम् ।।10।।
अन्वयः – यदा हृदिस्थानास्थितो वायुः वक्त्रं प्रपद्यते तद् व्यायामकुर्वतः जन्तोः बलार्धस्य लक्षणम्।
शब्दार्थाः – यदा = यस्मिन् काले (जिस समय), हृदिस्थानास्थितः = हृदयस्थले विद्यमानः (हृदय स्थल में विद्यमान), वायुः = वातः (हवा, वात), वकाम् = मुखम् (मुँह पर), प्रपद्यते = प्रवर्तते (प्रवर्तित होती है), तद् = असौ (वह), व्यायामकुर्वतः = व्यायामिनः (व्यायाम करने वाले का), जन्तोः = प्राणिनः (प्राणी के), बलार्धस्य = अर्धबलस्य, शक्तेः अर्धांशस्य (आधे सामर्थ्य, बल), लक्षणम् = सङ्केतम्, लक्षणस्य प्रतीतिः (लक्षण की प्रतीति है)।
सन्दर्भ-प्रसङ्गश्च – यह श्लोक हमारी शेमुषी पाठ्य पुस्तक के ‘व्यायामः सर्वदा पथ्यः’ पाठ से लिया गया है। यह पाठ आचार्य सुश्रुत-रचित सुश्रुत-संहिता आयुर्वेद ग्रन्थ से सङ्कलित है। इस श्लोक में आचार्य अर्धबल का लक्षण कहते हैं।
हिन्दी-अनुवादः – जिस समय (जब) हृदयस्थल में विद्यमान वात (हवा) मुख की ओर प्रवृत्त होती है तब व्यायाम करने वाले प्राणी के आधे बल (सामर्थ्य) का लक्षण (संकेत) प्रतीत होता है।

11. वयोबलशरीराणि देशकालाशनानि च।
समीक्ष्य कुर्याद् व्यायाममन्यथा रोगमाप्नुयात् ।।11।।
अन्वयः – वयः-बल-शरीराणि च देश-काल-अशनानि समीक्ष्य व्यायाम कुर्यात् अन्यथा रोगमाप्नुयात्।
शब्दार्थाः – वयः = आयुः, अवस्थाम् (उम्र), बल = शक्ति (ताकत), शरीराणि = गात्राणि (शरीर), च देश = स्थानम् (स्थान), काल = समय (समय), अशनानि = आहाराः, भोजनानि (भोजन को), समीक्ष्य = परीक्ष्य (परीक्षण करके/परख करके), व्यायाम = परिश्रमं (कसरत), कुर्यात् = कुर्वीत (करना चाहिए), अन्यथा = नोचेत् (नहीं तो, अन्यथा), रोगम् = रुग्णताम् (रोग), आप्नुयात् = लभते (प्राप्त करता है)।
सन्दर्भ-प्रसङ्गश्च-यह श्लोक हमारी शेमुषी पाठ्य पुस्तक के व्यायामः सर्वदा पथ्यः पाठ से लिया गया है। मूलतः यह पाठ आचार्य सुश्रुत-रचित ‘सुश्रुत-संहिता’ आयुर्वेद ग्रन्थ से संकलित है। इसमें आचार्य कहते हैं कि मनुष्य को व्यायाम अपनी आयु, बल, शारीरिक क्षमता, स्थान व उचित समय देख कर ही करना चाहिए।
हिन्दी-अनुवादः- (मनुष्य) आयु, बल, शरीर, स्थान, समय और भोजन का परीक्षण करके व्यायाम करे अन्यथा (नहीं तो) रुग्णता को प्राप्त होता है अर्थात् बीमार हो जाता है।