JAC Class 9 Maths Important Questions Chapter 8 Quadrilaterals

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 8 Quadrilaterals Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 8 Quadrilaterals

Question 1.
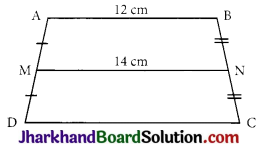
ABCD is a trapezium in which AB || DC. M and N are the mid-points of AD and BC respectively. If AB = 12 cm and MN = 14 cm, find CD.

Solution :
Here, ABCD is a trapezium in which, AB || DC and M and N are mid-points of AD and BC respectively. Since the line segment joining the midpoints of non-parallel sides of trapezium is half of the sum of the lengths of its parallel sides
⇒ MN = \(\frac {1}{2}\)(AB + CD)
⇒ 14 = \(\frac {1}{2}\)(12 + CD)
⇒ 28 = 12 + CD
⇒ CD = 28 – 12 = 16 cm

Question 2.
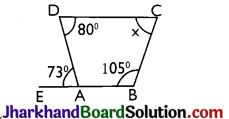
Use the informations given in figure below to calculate the value of x.

Solution :
Since, EB is a straight line.
∴ ∠DAE + ∠DAB = 180°
⇒ 73° + ∠DAB = 180°
i.e., ∠DAB = 180° – 73° = 107°
∴ ∠DAB + ∠ABC + ∠BCD + ∠CDA = 360°
Since the sum of the angles of quadrilateral ABCD is 360°
∴ 107° + 105° + x + 80° = 360°
⇒ 292° + x = 360°
⇒ x = 360° – 292° = 68°

Question 3.
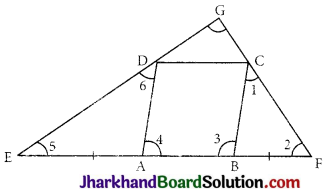
ABCD is a rhombus and AB is produced to E and F such that AE = AB = BF. Prove that EG and FG are perpendicular to each other.

Solution :
Given: ABCD is a rhombus. AB produced to E and F such that AE = AB = BF
Construction: Join ED and CF and produce it to meet at G.
To prove: ED ⊥ FC
Proof: AB is produced to points E and F such that AE = AB = BF …(i)
Also, since ABCD is a rhombus
AB = CD = BC = AD ……..(ii)
Now, in ΔBCF, BC = BF [From (i) and (ii)]
⇒ ∠1 = ∠2
∠3 = ∠1 + ∠2 [Exterior angle]
∠3 = 2∠2 ……..(iii)
Similarly, AE = AD
∠5 = ∠6 …(iv)
⇒ ∠4 = ∠5 + ∠6 = 2∠5
Adding (iii) and (iv) we get
∠4 + ∠3 = 2∠5 +2∠2
⇒ 180° = 2(∠5 + ∠2) [∵ ∠4 and ∠3 are consecutive interior angles]
⇒ ∠5 + ∠2 = 90°
∴ Now in ΔEGF
∠5 + ∠2 + ∠EGF = 180°
⇒ ED ⊥ FC
⇒ ∠EGF = 90° Hence Proved.

Question 4.
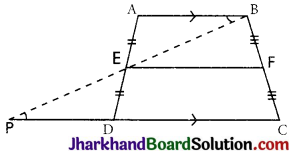
In the given figure, E and F are respectively, the mid-points of nonparallel sides of a trapezium ABCD. Prove that
(i) EF || AB
(ii) EF = \(\frac {1}{2}\)(AB + DC).

Solution :
Join BE and produce it to intersect CD produced at point P. In ΔAEB and ΔDEP, AB || PC and BP is transversal
⇒ ∠ABE – ∠DPE (Alternate interior angles)
∠AEB = ∠DEP (Vertically opposite angles)
And AE = DE (E is mid-point of AD)
⇒ ΔAEB ≅ ΔDEP (By AAS)
⇒ BE = PE [By CPCT]
And AB = DP [By CPCT]
Since the line segment joining the midpoints of any two sides of a triangle is parallel and half of the third side, therefore, in ΔBPC E is mid-point of BP [As, BE = PE]
and F is mid-point of BC [Given]
⇒ EF || PC and EF = \(\frac {1}{2}\)PC
⇒ EF || DC and EF = \(\frac {1}{2}\)(PD + DC)
⇒ EF || AB and EF = \(\frac {1}{2}\)(AB + DC) (As, DC || AB and PD = AB)
Hence, proved.

Multiple Choice Questions

Question 1.
In a parallelogram ABCD, ∠D = 105°, then the ∠A and ∠B will be :
(a) 105°, 75°
(b) 75°, 105°
(c) 105°, 105°
(d) 75°, 75°
Solution :
(b) 75°, 105°

Question 2.
In a parallelogram, ABCD diagonals AC and BD intersect at O and AC = 12.8 cm and BD = 7.6 cm, then the measures of OC and OD respectively equal to :
(a) 1.9 cm, 6.4 cm
(b) 3.8 cm, 3.2 cm
(c) 3.8 cm, 3.2 cm
(d) 6.4 cm, 3.8 cm
Solution :
(d) 6.4 cm, 3.8 cm

Question 3.
Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)° then the value of x will be :
(a) 17°
(b) 16°
(c) 15°
(d) 13°
Solution :
(d) 13°

Question 4.
When the diagonals of a parallelogram are perpendicular to each other then it is called a :
(a) Square
(b) Rectangle
(c) Rhombus
(d) Trapezium
Solution :
(c) Rhombus

Question 5.
In a parallelogram ABCD, E is the midpoint of side BC. If DE and AB when produced meet at F then: (a) AF = \(\frac {1}{2}\)AB
(b) AF = 2AB
(c) AF = 4AB
(d) Data Insufficient
Solution :
(b) AF = 2AB

Question 6.
ABCD is a rhombus with ∠ABC = 56°, then the ∠ACD will be:
(a) 56°
(b) 62°
(c) 124°
(d) 34°
Solution :
(b) 62°

Question 7.
In a triangle, P, Q and R are the midpoints of the sides BC, CA and AB respectively. If AC = 16 cm, BC = 20 cm and AB = 24 cm then the perimeter of the quadrilateral ARPQ will be:
(a) 60 cm
(b) 30 cm
(c) 40 cm
(d) None of these
Solution :
(c) 40 cm

Question 8.
LMNO is a trapezium with LM || NO. If P and Q are the mid-points of LO and MN respectively and LM = 5 cm and ON = 10 cm then PQ =
(a) 2.5 m
(b) 5 cm
(c) 7.5 cm
(d) 15 cm
Solution :
(c) 7.5 cm

Question 9.
In an isosceles trapezium ABCD if ∠A = 45° then ∠C will be:
(a) 90°
(b) 135°
(c) 125°
(d) None of these
Solution :
(b) 135°

Question 10.
In a right-angle triangle ABC is right-angled at B. Given that AB = 9 cm, AC = 15 cm and D, E are the mid-points of the sides AB and AC respectively, then the area of ΔADE =
(a) 67.5 cm²
(b) 13.5 cm²
(c) 27 cm²
(d) Data insufficient
Solution :
(b) 13.5 cm²

Question 11.
When the opposite sides of quadrilateral are parallel to each other then it is called a:
(a) Square
(b) Parallelogram
(c) Trapezium
(d) Rhombus
Solution :
(b) Parallelogram

Question 12.
In the given figure, AP and BP are angle bisectors of ∠A and ∠B which meet at P in the parallelogram ABCD. Then 2∠APB =

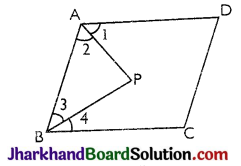
(a) ∠A + ∠B
(b) ∠A + ∠C
(c) ∠B + ∠D
(d) 2∠C + ∠B
Solution :
(a) ∠A + ∠B

Question 13.
In a quadrilateral ABCD, AO and DO are angle bisectors of ∠A and ∠D and given that ∠C = 105°, ∠B = 70° then the ∠AOD is :
(a) 67.5°
(b) 77.5°
(c) 87.5°
(d) 99.75°
Solution :
(c) 87.5°

Question 14.
In a parallelogram the sum of the angle bisectors of two adjacent angles is :
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution :
(d) 90°