Students should go through these JAC Class 9 Maths Notes Chapter 10 Circles will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 10 Circles
Definitions
→ Circle:
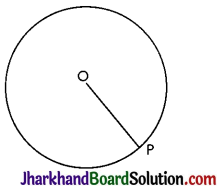
The collection of all the points in a plane, which are at a fixed distance from a fixed point in the plane, is called a circle. The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle.
In figure, O is the centre and the length OP is the radius of the circle. So the line segment joining the centre and any point on the circle is called a radius of the circle.
→ Interior and Exterior of a Circle:
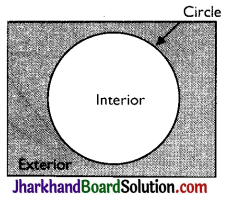
A circle divides the plane on which it lies into three parts. They are
(i) inside the circle (or interior of the circle)
(ii) the circle and
(iii) outside the circle (or exterior of the circle.)
The circle and its interior make up the circular region.
→ Chord:
If we take two points P and Q on a circle, then the line segment PQ is called a chord of the circle.
![]()
→ Diameter:
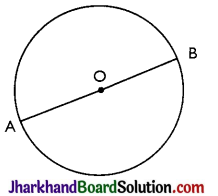
The chord which passes through the centre of the circle, is called a diameter of the circle.
A diameter is the longest chord and all diameters have the same length, which is equal to two times the radius. In figure, AOB is a diameter of circle.
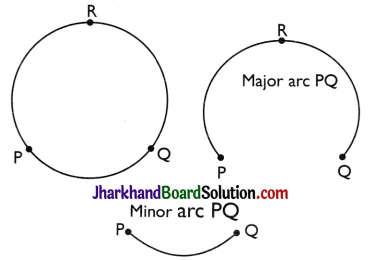
→ Arc:
A piece of a circle between two points is called an arc. If we look at the pieces of the circle between two points Pand Q in figure, we find that there are two pieces, one longer and the other smaller. The longer one is called the major arc PQ and the shorter one is called the minor arc PQ. The minor arc PQ is also denoted by PQ and the major arc PQ by PRO, where is some point on the are between P and Q. Unless otherwise stated, arc PQ or PQ stands for minor arc PQ. When P and Q are ends of a diameter, then both arcs are equal and each is called a semicircle.
→ Circumference: The length of the complete circle is called its circumference.
→ Segment:
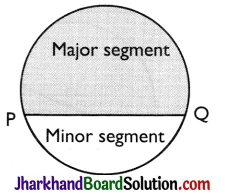
The region between a chord and either of its arcs is called a segment of the circular region or simply a segment of the circle. There are two types of segments which are the major segment and the minor segment (as in figure).
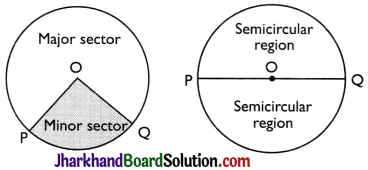
→ Sector:
The region between an arc and the two radil, joining the centre to the end points of the arc is called a sector. Like segments, we find that the minor arc corresponds to the minor sector and the major arc corresponds to the major sector. In figure, the region OPQ is the minor sector and the remaining part of the circular region is the major sector. When two arcs are equal, then both segments and both sectors become the same and each is known as a semicircular region.
Theorem 1.
Equal chords of a circle subtend equal angles at the centre.
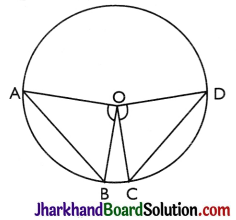
Given: AB and CD are the two equal chords of a circle with centre O.
To Prove: ∠AOB = ∠COD.
Proof:
In ΔAOB and ΔCOD,
OA = OC [Radii of a circle]
OB = OD [Radii of a circle]
AB = CD [Given]
∴ ΔAOB ≅ ΔCOD [By SSS]
∴ ∠AOB = ∠COD. [By CPCT]
Converse of above Theorem:
If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.
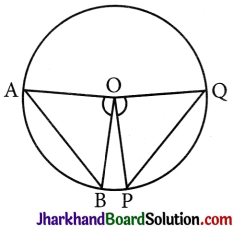
Given: ∠AOB and ∠POQ are two equal angles subtended by chords AB and PQ of a circle at its centre O.
To Prove: AB = PQ
Proof:
In ΔAOB and ΔPOQ.
OA = OP [Radii of a circle]
OB = OQ [Radii of a circle]
∠AOB = ∠POQ [Given]
∴ ΔAOB ≅ ΔPOQ [By SAS]
∴ AB = PQ [By CPCT]
Hence, proved.
![]()
Theorem 2.
The perpendicular from the centre of a circle to a chord bisects the chord.
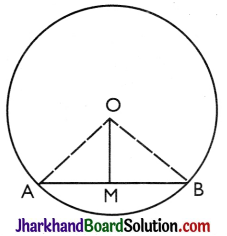
Given: A circle with centre O. AB is a chord of this circle OM ⊥ AB.
To Prove: MA = MB.
Construction: Join OA and OB.
Proof:
In right triangles OMA and OMB.
OA = OB [Radii of a circle]
OM = OM [Common]
∠OMA = ∠OMB [90° each]
∴ ΔOMA ≅ ΔOMB [By RHS]
∴ MA = BR [By CPCT]
Hence, proved.
Converse of above Theorem:
The line drawn through the centre of a circle to bisect a chord is a perpendicular to the chord.
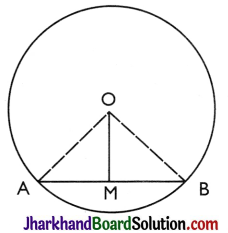
Given: A circle with centre O. AB is a chord of this circle whose mid-point is M.
To Prove: OM ⊥ AB
Construction: Join OA and OB.
Proof:
In ΔOMA and ΔOMB,
MA = MB [Given]
OM = OM [Common]3
ОА = ОВ [Radii of a circle]
∴ ΔOMA ≅ ΔOMB [By SSS]
∴ ∠AMO = ∠BMO [By CPCT]
But, ∠AMO + ∠BMO = 180° [Linear pair axiom]
∴ ∠AMO = ∠BMO = 90°
⇒ OM ⊥ AB.
Theorem 3.
There is one and only one circle passing through three given non-collinear points.
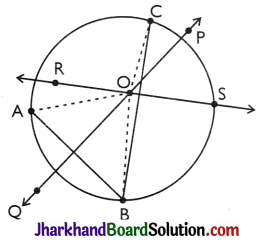
Proof:
Let us take three points A, B and C, which are not on the same line, or in other words, they are not collinear [as in figure]. Draw perpendicular bisectors of AB and BC say, PQ and RS respectively. Let these perpendicular bisectors intersect at one point O. (Note that PQ and RS will intersect because they are not parallel) (as in figure).
∴ Olies on the perpendicular bisector PQ of AB.
∴ OA = OB
[ Every point on the perpendicular bisector of a line segment is equidistant from its end points]
∴ Similarly : Olies on the perpendicular bisector RS of BC.
∴ OB = OC
[∵ Every point on the perpendicular bisector of a line segment is equidistant from its end points]
So, OA = OB = OC
i.e., the points A, B and C are at equal distances from the point O.
So, if we draw a circle with centre O and radius OA it will also pass through B and C. This shows that there is a circle passing through the three points A, B and C. We know that two lines (perpendicular bisectors) can intersect at only one point. so we can draw only one circle with radius OA. In other words, there is a unique circle passing through A, B and C. Hence Proved.
Remark:
If ABC is a triangle, then by above theorem, there is a unique circle passing through the three vertices A, B and C of the triangle. This circle is the circumcircle of the ΔABC. Its centre and radius are called respectively the circumcentre and the circumradius of the triangle.
![]()
Theorem 4.
Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).
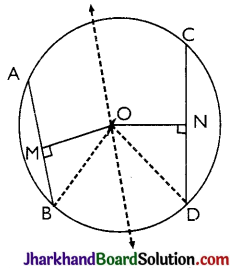
Given: A circle has two equalchords AB and CD.
So, AB = CD and OM ⊥ AB, ON ⊥ CD.
To Prove: OM = ON
Construction: Join OB and OD.
Proof:
AB = CD (Given)
∴ \(\frac{1}{2}\)AB = \(\frac{1}{2}\)CD
⇒ BM = DN
[∵ The perpendicular drawn from the centre of a circle to the chord bisect the chord.]
In ΔΟΜB and ΔOND,
∠OMB = ∠OND = 90° [Given]
OB = OD [Radii of same circle]
BM = DN [Proved above]
∴ ΔOMB ≅ ΔOND [By RHS]
OM = ON [By CPCT]
Hence, proved.
Remark: Chords equidistant from the centre of a circle are equal in length.
Some Important Theorems
Theorem 1.
If the angles subtended by the chords at the centre of a circleare equal then the chords are equal.
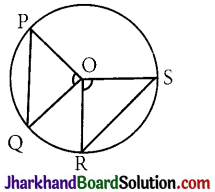
Given: A circle with centre O. Chords PQ and RS subtend equal angles at the center of the circle.
i.e. ∠POQ = ∠ROS
To Prove: Chord PQ = chord RS.
Proof:
In ΔPOQ and ΔROS
∠POQ = ∠ROS [Given]
OP = OR [Radii of the same circle]
OQ = OS [Radii of the same circle]
⇒ ΔPOQ ≅ ΔROS [By SAS]
⇒ chord PQ = chord RS [By CPCT]
Hence, proved.
Corollary 1: Two ares of a circle are congruent, if the angles subtended by them at the centre are equal.
Corollary 2: If two arcs of a circle are equal, they subtend equal angles at the centre.
Corollary 3: If two arcs of a circle are congruent (equal), their corresponding chords are also equal. Conversely, if two chords of a circle are equal, their corresponding arcs are also equal
∠AOB = ∠COD
∴ Chord AB = Chord CD
∴ Arc APB = Arc CQD.
![]()
Theorem 2.
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Given: An arc PQ of a circle subtending angles POQ at the centre and PAQ at a point A on the remaining part of the circle.
To Prove: ∠POQ = 2∠PAQ.
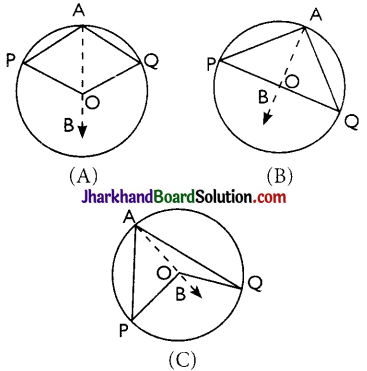
Construction: Join AO and extend it to a point B.
Proof:
There arises three cases:
(A) arc PQ is minor
(B) arc PQ is a semi-circle
(C) arc PQ is major.
In all the cases,
∠BOQ = ∠OAQ + ∠AQO ….(i)
[∵ An exterior angle of triangle is equal to the sum of the two interior opposite angles]
In OAO,
OA = OQ [Radil of a circle]
∠OAQ = ∠OQA …..(ii)
[Angles opposite to equal sides of a triangle are equal]
From (i) and (ii),
∠BOQ = 2∠OAQ ……(iii)
Similarly,
∠BOP = 2∠OAP ……(iv)
Adding (i) and (iv), we get
∠BOP + ∠BOQ = 2(∠OAP + ∠OAQ)
⇒ ∠POQ = 2∠PAQ ….(v)
NOTE: For the case (C), where PQ is the major arc, angle is replaced by reflex angles
Thus, ∠POQ = 2∠PAQ.
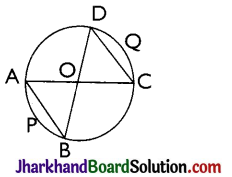
Theorem 3.
Angles in the same segment of a circle are equal.
Proof:
Let P and Q be any two points on a circle to form a chord PQ, A and C any other points on the remaining part of the circle and O be the centre of the circle. Then,
∠POQ = 2∠PAQ ……(i)
And ∠POQ = 2∠PCQ ……(ii)
From above equations, we get
2∠PAQ = 2∠PCQ
⇒ ∠PAQ = ∠PCQ Hence, proved
![]()
Theorem 4.
Angle in the semicircle is a right angle.
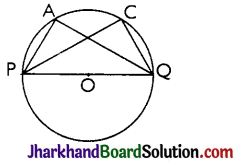
Proof:
∠PAQ is an angle in the segment, which is a semicircle.
∴ ∠PAQ = \(\frac{1}{2}\)∠POQ = \(\frac{1}{2}\) × 180° = 90°
[∵ ∠POQ is straight line angle or ∠POQ = 180°]
If we take any other point C on the semicircle then again we get
∠PCQ = \(\frac{1}{2}\)∠POQ = \(\frac{1}{2}\) × 180° = 90°
Hence, proved.
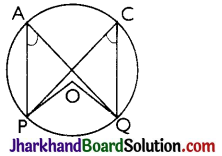
Theorem 5.
If a line segment joining two points subtends equal angles at two other points lying on the same side of the line segment then the four points lie on a circle (i.e., they are concyclic).
Given: AB is a line segment, which subtends equal angles at two points C and D i.e, ∠ACB = ∠ADB.
To Prove: The points A, B, C and D lie on a circle.
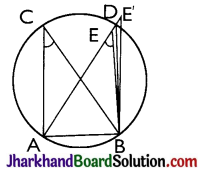
Proof:
Let us draw a circle through the points A, C and B. Suppose it does not pass through the point D.
Then it will intersect AD (or extended AD) at a point, say E (or E’). If points A, C, E and B lie on a circle.
∠ACB = ∠AEB [∵ Angles in the same segment of circle are equal]
But it is given that, ∠ACB = ∠ADB
Therefore, ∠AEB = ∠ADB
This is possibleonly when Ecoincides with D.
[As otherwise ∠AEB > ∠ADB]
Similarly, E’ should also coincide with D.
So A, B, C and D are concyclic.
Hence, proved.
Cyclic Quadrilateral
A quadrilateral ABCD is called cyclic if all the four vertices of it lie on a circle.
![]()
Theorem 6.
The sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
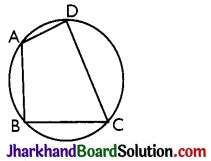
Given: A cyclic quadrilateral ABCD.
To Prove: ∠A + ∠C = ∠B + ∠D = 180°
Construction: Join AC and BD.
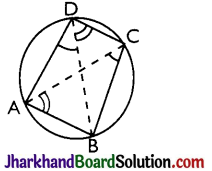
Proof:
∠ACB = ∠ADB [Angles in the same segment]
And ∠BAC = ∠BDC [Angles in the same segment]
∴ ∠ACB + ∠BAC = ∠ADB + ∠BDC
= ∠ADC.
Adding ∠ABC to both sides, we get
∠ACB + ∠BAC + ∠ABC = ∠ADC + ∠ABC
The left side being the sum of three angles of AABC is equal to 180°.
∴ ∠ADC + ∠ABC = 180°
i.e, ∠D + ∠B = 180°
∴ ∠A + ∠C = 360° – (∠B + ∠D) = 180°
[∵ ∠A + ∠B + ∠C + ∠D = 360°]
Hence, proved.
Corollary: If the sum of a pair of opposite angles of a quadrilateral is 180°, then quadrilateral is cyclic.