Jharkhand Board JAC Class 9 Maths Important Questions Chapter 7 Triangles Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 7 Triangles
Question 1.
If D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD = \(\frac {1}{2}\)AC.
Solution :
Let ΔABC is a right triangle such that ∠B = 90° and D is midpoint of AC then we have to prove that BD = \(\frac {1}{2}\)AC, we produce BD to E such that BD = DE and join EC
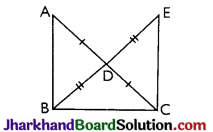
Now, in ΔADB and ΔCDE we have
AD = DC (Given)
BD = DE (By construction)
And, ∠ADB = ∠CDE
[Vertically opposite angles]
∴ By SAS criterion of congruence, we have
ΔADB ≅ ΔCDE
⇒ EC = AB and ∠CED = ∠ABD ….(i)
(By CPCT)
But ∠CED and ∠ABD are alternate interior angles .
∴ CE || AB ⇒ ∠ABC + ∠ECB = 180°
(interior angles)
⇒ 90° + ∠ECB = 180°
⇒ ∠ECB = 90°
Now, in ΔABC and ΔECB, we have
AB = EC [By (i)]
BC = BC [Common]
And, ∠ABC = ∠ECB = 90°
∴ BY SAS criterion of congruence
ΔABC ≅ ΔECB
⇒ AC = EB = 2BD [By CPCT and also D is a midpoint of AC and BE]
⇒ BD = \(\frac {1}{2}\) AC Hence, proved.
![]()
Question 2.
In a right-angled triangle, one acute angle is double the other. Prove that the hypotenuse is double the smallest side.
Solution :
Let ΔABC is a right triangle such that ∠B = 90° and ∠ACB = 2∠CAB, then we have to prove AC = 2BC. We produce CB to D such that BD = CB and join AD. Let
⇒ ∠ACB = 2x and ∠CAB = x
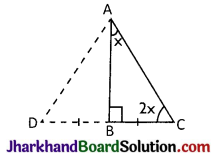
Proof: In ΔABD and ΔABC, we have
BD = BC (By construction)
AB = AB [Common]
∠ABD = ∠ABC = 90°
∴ By SAS criterion of congruence we get
ΔABD ≅ ΔABC
⇒ AD = AC and ∠DAB = ∠CAB
(By CPCT)
⇒ AD = AC and ∠DAB = x[∵ ∠CAB = x]
Now, ∠DAC = ∠DAB + ∠CAB = x + x = 2x
∴ ∠DAC = ∠ACD
⇒ DC = AD
[Sides opposite to equal angles] (∵ DC = 2BC)
⇒ 2BC = AD
⇒ 2BC = AC (AD = AC)
Hence, Proved.
Question 3.
In figure, T is a point on side QR of ΔPQR and S is a point such that RT = ST. Prove that PQ + PR > QS.
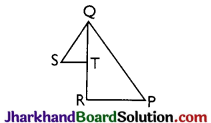
Solution :
In ΔPQR we have
PQ + PR > QR
⇒ PQ + PR > QT + TR
⇒ PQ + PR > QT + ST
[∵ RT = ST]
In ΔQST, QT + ST > SQ
∴ PQ + PR > SQ Hence, proved.
![]()
Question 4.
In the given figure, PQ = QR and ∠x = ∠y. Prove that AR = PB.
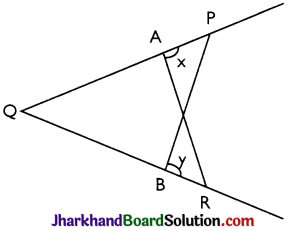
Solution :
Proof: In the figure, ∠QAR + ∠PAR = 180°(Linear pair axiom)
⇒ ∠QAR + ∠x = 180°
⇒ ∠QAR = 180° – ∠x°
Similarly ∠QBP + ∠RBP = 180° (Linear pair axiom)
⇒ ∠QBP + ∠y = 180°
⇒ ∠QBP = 180° – ∠y …(ii)
But given, ∠x = ∠y
∴ ∠QAR = ∠QBP [From (i) and (ii)]
Now, in ΔQAR and ΔQBP, QR = PQ (Given)
∠QAR = ∠QBP (As proved above)
∠Q = ∠Q (Common)
⇒ ΔQAR = ΔQBP
(AAS congruence rule)
⇒ AR = PB (CPCT)
Hence proved.
Question 5.
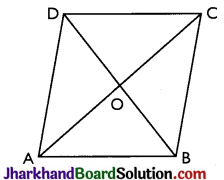
Diagonal AC and BD of quadrilateral ABCD intersect each other at O. Prove that
(i) AB + BC + CD + DA > AC + BD
(ii) AB + BC + CD + DA < 2 (AC + BD)
Solution :
Given: AC and BD are the diagonals of quadrilateral ABCD. (i) To prove: AB + BC + CD + DA > AC + BD
Proof: We know that the sum of any two sides of a triangle is always greater than the third side. Therefore,
In ΔABC, AB + BC > AC …(i)
In ΔBCD, BC + CD > BD …(ii)
In ΔCDA CD + DA > CA …(iii)
In ΔABD, AB + AD > BD …(iv)
Adding (i), (ii), (iii) and (iv), we get
2 (AB + BC + CD + DA) > 2 (AC + BD)
⇒ AB + BC + CD + DA > AC + BD
Hence proved.
(i) To prove: AB + BC + CD + DA < 2 (AC + BD) Proof : In ΔOAB, OA + OB > AB ……(i)
In ΔBOC, OB + OC > BC …(ii)
In ΔCOD, OC + OD > CD …(iii)
In ΔAOD, OA + OD > DA …(iv)
Adding (i), (ii), (iii) and (iv), we get
2 (OA + OB + OC + OD) > AB + BC + CD + DA
2 [(OA + OC) + (OB + OD)] > AB + BC + CD + DA
2 (AC + BD) > AB + BC + CD + DA
AB + BC + CD + DA < 2 (AC + BD)
Hence proved
Multiple Choice Questions
Question 1.
If the three altitudes of a Δ are equal then triangle is :
(a) isosceles
(b) equilateral
(c) right-angled
(d) none
Solution :
(b) equilateral
![]()
Question 2.
ABCD is a square and P, Q, R are points on AB, BC and CD respectively such that AP = BQ = CR and ∠PQR = 90°, then ∠QPR =
(a) 45°
(b) 50°
(c) 60°
(d) 75°
Solution :
(a) 45°
Question 3.
In a ΔXYZ, LM ⊥ YZ and bisectors YN and ZN of ∠Y and ∠Z respectively meet at Non LM then YL + ZM =
(a) YZ
(b) XY
(c) XZ
(d) LM
Solution :
(d) LM
![]()
Question 4.
In a ΔPQR, PS is bisector of ∠P and ∠Q = 70°, ∠R = 30°, then
(a) QS > PQ > PR
(b) QS < PQ < PR
(c) PQ > QS > SR
(d) PQ < QS < SR
Solution :
(b) QS < PQ < PR
Question 5.
If D is any point on the side BC of a ΔABC, then:
(a) AB + BC + CA > 2AD
(b) AB + BC + CA < 2AD
(c) AB + BC + CA > 3AD
(d) None of these
Solution :
(a) AB + BC + CA > 2AD
Question 6.
For given figure, which one is correct:
(a) ΔABC ≅ ΔDEP
(b) ΔABC ≅ ΔFED
(c) ΔABC ≅ ΔDFE
(d) ΔABC ≅ ΔEDF
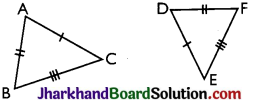
Solution :
(a) ΔABC ≅ ΔDEP
![]()
Question 7.
In a right-angled triangle, one acute angle is double the other then the hypotenuse is :
(a) Equal to the smallest side
(b) Double the smallest side
(c) Triple the smallest side
(d) None of these
Solution :
(d) None of these