JAC Class 9 Science Important Questions Chapter 10 Gravitation

JAC Board Class 9th Science Important Questions Chapter 10 Gravitation

Multiple Choice Questions 

Question 1.
The mass of a body on moon is 40 kg. What is its weight on the earth?
(a) 240 kg
(b) 392 N
(c) 240 N
(c) 400 kg
Answer:
(b) 392 N

Question 2.
The gravitational force between two objects is
(a) attractive at large distance only
(b) attractive at small distance only
(c) attractive at all distances
(d) attractive at large distance but repulsive at small distance
Answer:
(c) attractive at all distances

Question 3.
A body of mass 1 kg is attracted by the earth with a force equal to
(a) 9.8 N
(b) 1 N
(c) 6.67 × 10¹¹ N
(d) 9.8 m/s
Answer:
(a) 9.8 N

Question 4.
The earth attracts a body with a force of 10 N. With what force does that the body attract the earth?
(a) 10N
(b) 1 N
(c) \(\frac{1}{10 \mathrm{~N}}\)
(d) 2 N
Answer:
(a) 10N

Question 5.
The SI unit of G is
(a) Nm² kg^-1
(b) Nm² kg^-2
(c) Nm² kg
(d) N^-1 m² kg^-2
Answer:
(b) Nm² kg^-2

Question 6.
The gravitational force of attraction between two bodies of 1 kg each and 1 m apart is
(a) 6.67 × 10^-11 N
(b) 6.67 × 10^-8 N
(c) 6.67 × 10¹¹ N
(d) 6.67 × 10⁸ N
Answer:
(a) 6.67 × 10^-11 N

Question 7.
The value of acceleration due to gravity near the earth’s surface is
(a) 8.9 m^-2
(b) 9.8 ms^-2
(c) 8.9 cms^-2
(d) 9.8 cms^-2
Answer:
(b) 9.8 ms^-2

Question 8.
Consider an elevator moving downwards with an acceleration a The force exerted by a passenger of mass m on the floor of the elevator is
(a) ma
(b) ma – mg
(c) mg – ma
(d) mg + ma
Answer:
(c) mg – ma

Question 9.
If the earth suddenly shrinks to half of its present size, the value of acceleration due to gravity will
(a) become twice
(b) remain unchanged
(c) become half
(d) become four times
Answer:
(d) become four times

Question 10.
The weight of a body would not be zero
(a) at the centre of the earth
(b) during a free fall of an elevator
(c) in interplanetary space
(d) on a frictionless surface
Answer:
(d) on a frictionless surface

Question 11.
Newton’s law of gravitation
(a) can be verified in a laboratory
(b) cannot be verified but is true
(c) is valid only on earth
(d) is valid only in the solar system
Answer:
(a) can be verified in a laboratory

Question 12.
10 kg weight is equal to
(a) 9.8 N
(b) 98 N
(c) 980 N
(d) \(\frac{1}{9.8}\) N
Answer:
(b) 98 N

Question 13.
The weight of a body cannot be expressed in
(a) kg wt
(b) N
(c) dyne
(d) kg
Answer:
(d) kg

Question 14.
A stone is dropped from a cliff. Its speed after it has fallen 100m is
(a) 9.8 m/s
(b) 44.2 m/s
(c) 19.8 m/s
(d) 98 m/s
Answer:
(b) 44.2 m/s

Question 15.
At which of the following locations, the value of g is the largest?
(a) On top of the Mount Everest
(b) On top of Qutub Minar
(c) At a place on the equator
(d) A camp site in Antarctica
Answer:
(d) A camp site in Antarctica

Analysing & Evaluating Questions

Question 16.
An apple falls from a tree because of gravitational attraction between the earth and apple. If Ft is the magnitude of force exerted by the earth on the apple and F2 is the magnitude of force exerted by the apple on the earth, then
(a) F₁ is very much greater than F₂
(b) F₂ is very much greater than F₁
(c) F₁ is only a little greater than F₂
(d) F₁ and F₂ are equal
Answer:
(d) F₁ and F₂ are equal

Question 17.
An object is put one by one in three liquids having differei dnsities. The object floats with\(\frac{1}{9}\), \(\frac{2}{11}\) and \(\frac{3}{7}\) part of its volume outside dit liquid surface in liquids of densities d₁, d₂ and d₃ respectively. Which of the following is correct?
(a) d₁ > d₂ > d₃
(b) d₁ >d₂ <d₃
(c) d₁ < d₂ > d₃
(d) d₁ < d₂ < d₃
Answer:
(d) d₁ < d₂ < d₃

Question 18.
An object weighs 10N in air. When immersed fully in water, it weighs only 8N. The weight of the liquid displaced by the object will be
(a) 2 N
(b) 8 N
(c) 10 N
(d) 12
Answer:
(a) 2 N

Assertion Reason Questions

Directions: In the following questions, the Assertions and the Reasons have been put forward. Read the statements carefully and choose the correct alternative from the following:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.
(B) The assertion and the reason are correct but the reason is not the correct explanation of the assertion.
(C) The assertion is true but the reason is false.
(D) Both the statements are false.
1. Assertion: The law of gravitation is not applicable on the two bodies lying on the surface of the earth.
Reason: Law of gravitation is applied to celestial bodies only.
Answer:
(D) Both the statements are false.

2. Assertion: Mass of a body remains same at all the places.
Reason: Mass of a body is independent of acceleration due to gravity.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.

3. Assertion: Value of acceleration due to gravity is greater at the poles than at the equator.
Reason: Distance between pole and the centre of the earth is less than the distance between the equator and the centre of the earth.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.

4. Assertion: One can jump higher on the surface of the moon than on the earth. Reason: The value of g (acceleration due to gravity) on the moon is greater than that on the earth.
Answer:
(C) The assertion is true but the reason is false.

5. Assertion: Fluids exert an upthrust on the objects immersed in them.
Reason: The upthrust is equal to the weight of the liquid displaced.
Answer:
(B) The assertion and the reason are correct but the reason is not the correct explanation of the assertion.

Very Short Answer Type Questions

Question 1.
Define the term ‘gravitation’.
Answer:
Every object in this universe attracts every other object with a force known as ‘force of gravitation’. Gravitation is the force of attraction between any two bodies in the universe.

Question 2.
Give the SI unit and value of G.
Answer:
SI unit of G = \(\frac{\mathrm{Nm}^{2}}{\mathrm{~kg} \cdot \mathrm{kg}}\) = N m² kg^-2
Its value = 6.67 × 10^-11 N m² kg^-2.

Question 3.
g = GM/R², what do the symbols in this formula denote?
Answer:
g = Acceleration due to gravity
G = Gravitational constant
M = Mass of the earth
R = Radius of the earth

Question 4.
Name the scientist who first determined the value of G experimentally.
Answer:
Henry Cavendish first determined the value of G experimentally, in the year 1778, using a sensitive balance.

Question 5.
Why is G called a universal gravitational constant’?
Answer:
The value of constant G is same for any pair of objects in the universe. Also, its value does not depend on the nature of the intervening medium. That is why constant G is called ‘universal’, whether the bodies are big or small, or whether they are celestial or terrestrial.

Question 6.
State any two properties of gravitational force.
Answer:

1. It is always attractive in nature.
2. It does not depend on the nature of the medium between the two bodies.

Question 7.
Which force is responsible for the stability of our universe?
Answer:
The force of gravitation.

Question 8.
How is ‘g’ on the surface of the earth related to ‘G’?
Answer:
g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\) = \(\frac{1.67 \times\left(1.74 \times 10^{6}\right)^{2}}{6.67 \times 10^{-11}}\)

where M = mass of the earth,
R = radius of the earth.

Question 9.
How is weight of an object related to its mass?
Answer:
Weight (w) = mass (m) × acceleration due to gravity (g).

Question 10.
What is the SI unit of pressure?
Answer:
The SI unit of pressure = N/m² = Pascal.

Question 11.
Define thrust. What is the SI unit of thrust?
Answer:
The net force exerted by a body in a particular direction is called thrust. The SI unit of thrust is newton.

Question 12.
Why does a truck or a motorbike have much wider tyres?
Answer:
A truck or a motorbike has much wider types so that the pressure exerted by it can be distributed to more surface area of the road and avoid the wear and tear of tyres.

Question 13.
In what sense does the moon fall towards the earth? Why does it not actually fall on the earth’s surface?
Answer:
At each point of its orbit, the moon falls towards the earth instead of going straight. It does not fall on the earth because it is moving in a circular orbit. The moon is kept in its circular orbit by the centripetal force provided by the force of attraction of the earth.

Question 14.
The earth attracts an apple from the tree and it falls but the earth does not appear to move towards the apple. Why?
Answer:
The mass of the earth is extremely large as compared to that of the apple. So the acceleration produced is very small as compared to that in the apple. Hence, the motion of the earth towards the apple is not noticeable.

Question 15.
What do you mean by the term ‘free fall’?
Answer:
The motion of a body under the influence of the force of gravity alone is called a ‘free fall’.

Question 16.
Suppose a planet exists whose mass and radius, both are half that of the earth. Calculate the acceleration due to gravity on the surface of this planet.
Answer:
On the surface of the earth, g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
On the surface of the planet, \(g^{\prime}=\frac{G\left(\frac{M}{2}\right)}{\left(\frac{R}{2}\right)^{2}}=\frac{2 G M}{R^{2}}=2 g\)

Question 17.
Define mass of a body. What is its SI unit?
Answer:
The mass of a body represents the quantity of matter contained in the body. It gives a measure of inertia of the body. The greater the mass of a body, the greater is its inertia. The SI unit of mass is kilogram (kg).

Question 18.
Define one kilogram – weight. How many newtons are there in 1kg wt?
Answer:
One kilogram – weight (kg – wt)
= 1kg × 9.8 m/s² = 9.8 N.

Question 19.
State Archimedes’ principle.
Answer:
This principle states that when a body is immersed fully or partially in a fluid, it experiences an upward thrust equal to the weight of the fluid displaced by it.

Analysing & Evaluating Questions

Question 20.
A beam balance is used for measuring the mass of a body, whereas a spring balance gives the weight of a body. What is measured by a digital balance?
Answer:
Digital balance measures the weight of a body.

Question 21.
Under what conditions do the two hollow balls – one of aluminium and the other of iron, experience equal upthrust when placed in water?
Answer:
The two balls will experience equal upthrust in water when their volumes inside the water are equal.

Question 22.
The density of liquid B is greater than that of liquid A. A hydrometer is placed one by one in the two liquids. In which liquid will the hydrometer sink to the greater depth?
Answer:
The hydrometer will sink deeper in liquid A.

Short Answer Type Questions

Question 1.
During free – fall of an elevator, what is the weight of a body inside it? Give reasons for your answer.
Answer:
During free – fall of an elevator the apparent weight of the object becomes zero. This is because both the body and the elevator are in free fall, and have a downward acceleration of ‘g’. In this situation normal reaction on the body becomes zero. Since normal reaction is responsible for the sensation of weight in a body, the apparent weight of the body in this case becomes zero.

Question 2.
What is relative density?
Answer:
The relative density of a substance is the ratio of its density to that of the water at 4°C. Relative density Density of the substance Density of water at 4°C

Question 3.
Differentiate between ‘g’ and ‘G’ in tabular form.
Answer:

Acceleration due to gravity ‘g’	Universal gravitational constant ‘G’
(a) It is the acceleration acquired by a body due to earth’s gravitational pull on it.	(a) It is numerically equal to the force of attraction between two masses of 1kg each separated by a distance of 1 m.
(b) ‘g’ is not a universal constant. It is different at different places on the surface of the earth. Its value varies from one celestial body to another.	(b) ‘G’ is a universal constant and its value is same, i.e., 6.67 × 10-11 N m2 kg-2 everywhere in the universe.
(c) It is a vector quantity.	(c) It is a scalar quantity.

Question 4.
Why is it easier to swim in sea water than in river water?
Answer:
The density of sea water is high due to dissolved salts in it as compared to the density of river water. Hence, the buoyant force applied on the swimmer by the sea water is high which helps in floating and makes swimming simpler.

Question 5.
A ship made of iron does not sink but an iron nail sinks in water. Why?
Answer:
The iron nail sinks because of its high density and less buoyant force acting on it due to lesser surface area. Whereas, the surface area of a ship is greater and thus experiences a higher buoyant force. Due to this fact, a ship floats but an iron nail sinks.

Question 6.
A stone and feather are thrown from a tower. Both the objects should reach the ground at the same time but it does not happen. Give reasons.
Answer:
As per the motion of objects due to gravitational pull of the earth, both the bodies are acted upon by the same force of the earth but the stone will fall first and then the feather. Feather being lighter, experiences greater air resistance, so it will reach later.

Question 7.
The relative density of gold is 18.3. The density of water is 10³ kg/m³? What is the density of gold in S.I units?
Answer:
The relative density of gold is 18.3.
Relative density of gold = \(\frac{Density of gold}{Density of water}\)
That is, density of gold = Relative density of gold × Density of water = 18.3 × 10³ kg/m³ = 18300 kg/m³.

Question 8.
The acceleration due to gravity at the moon’s surface is 1.67 m/s². If the radius of the moon is 1.74 × 106m, calculate the mass of the moon.
Answer:
Here, G = 6.67 × 10^-11 Nm²/kg²
g = 1.67 m/s²
R= 1.74 × 10⁶ m.
Mass of the moon is
M = \(\frac{\mathrm{gR}^{2}}{\mathrm{G}}\) = \(\frac{1.67 \times\left(1.74 \times 10^{6}\right)^{2}}{6.67 \times 10^{-11}}\)
= 7.58 × 10²² kg.

Question 9.
Derive the formula for the gravitational force acting between two objects.
Answer:
Let two objects A and B of masses ‘M’ and’m’, lie at a distance d from each other as shown in the figure.

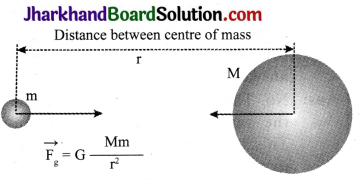
Let the force of attraction between two objects be F.
According to the universal law of gravitation, the force between two objects is directly proportional to the product of their masses.
F ∝ Mm … (1)
And the force between two objects is inversely proportional to the square of the distance between them,
F ∝ \(\frac{1}{\mathrm{~d}^{2}}\) …………(2)
F ∝ \(\frac{\mathrm{Mm}}{\mathrm{d}^{2}}\)
where G is universal gravitational constant

Question 10.
Find the value of ‘g’, acceleration due to gravity.
Answer:
g = \( \frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
G = 6.67 × 10^-11 Nm²/kg² (constant)
M = 6 × 10²⁴ kg (mass of the earth)
= \( \frac{6.7 \times 10^{-11} \mathrm{Nm}^{2} / \mathrm{kg}^{2} \times 6 \times 10^{24} \mathrm{~kg}}{\left(6.4 \times 10^{6} \mathrm{~m}\right)^{2}}\)
= 9.8 m/s²

Question 11.
Camels can walk easily on desert sand but we are not comfortable walking on the sand. Why do you think so?
Answer:
The surface area of a camel’s feet is broad and large. Thus, the pressure exerted is low. However, when we walk, our legs sink because the pressure exerted by our body is not equally distributed but is directed towards the legs.

Question 12.
Define lactometer and hydrometer.
Answer:
Lactometer is a device used to find the purity of milk. Hydrometer is a device used to find the density of a liquid.

Question 13.
Two wood pieces of same size and mass are dipped in two beakers containing water and oil. One wood floats on water, but the other one sinks in oil. Why?
Answer:
The wood floats on water because the density of wood is lower than the density of water, and the other wood sinks in the oil because the density of wood is more than that of the oil.

Question 14.
What are fluids? Why is Archimedes’ principle applicable only for fluids? Give the applications of Archimedes’ principle.
Answer:
Liquids are the substances which can flow. Archimedes principle is based on the upward force exerted by fluids on any object immersed in them. Hence, it is applicable only for fluids. Applications of Archimedes’ principle are as follows:

1. It is used to design ships and submarines.
2. To determine the purity of milk using lactometers which are designed based on the Archimedes’ principle.
3. To make hydrometers which are used to determine the density of liquids.

Question 15.
The volume of 60g of a substance is 10cm². If the density of water is 1g/cm², find out whether the substance will float or sink in water.
Answer:
Mass = 60g
Volume = 10 cm³
The density of water is 1g/cm². As the density of the given substance is more than the density of water, the substance will get submerged in water.

Question 16.
What is meant by buoyancy?
Answer:
When a body is submerged in a fluid, the fluid exerts an upward force on the submerged body. This upward force is equal to the weight of the fluid displaced by the submerged body and is called the buoyant force. In other words, it is the force exerted by the fluid when an object is submerged in it.

Analysing & Evaluating Questions

Question 17.
Identical packets are dropped from two aeroplanes, one over the equator and the other over the north pole, both from the height h. Assuming that all conditions are identical, explain if those packets take same time to reach the surface of earth or not. Justify your answer.
Answer:
No. The two packets will take different time intervals to reach the earth’s surface. This is because the acceleration due to gravity (g) is greater at the poles than that at the equator. The packet will fall slowly at the equator than that at the north pole.

Question 18.
You must have seen two types of balances. A grocer has a balance with two platforms or pan, and a needle moving on a scale. Some junk dealers (kabadiwalas) may be using a spring balance to weigh used newspapers. Suppose, the two balances give the same measure for a given body on the earth. Now, you take the balances to the moon. Would the two balances give the same measure? Explain your answer.
Answer:
No. The two balances will not give the same measure on the moon. This is because, the spring balance measures the weight, and the grocer’s balance measures the mass. The weight of a body depends upon the acceleration due to gravity at the place of measurement. The acceleration due to gravity on the moon is not equal to that on the earth. Therefore, spring balance will give different readings relative to the grocer’s balance on the moon.

Long Answer Type Questions

Question 1.
What is centripetal force? From where does the moon get the centripetal force required for its motion around the earth?
Answer:

1. Centripetal force When a body moves along a circular path with a uniform speed, its direction of motion changes at every point. The change in direction involves change in velocity or acceleration.
2. The force that provides this acceleration and keeps the body moving along the circular path, acts towards the centre. This force is called centripetal (centre seeking) force.
3. Therefore, a force which is required to make a body move along a circular path with uniform speed is called centripetal force. Centripetal force always acts along the radius and towards the centre of the circular path.
   
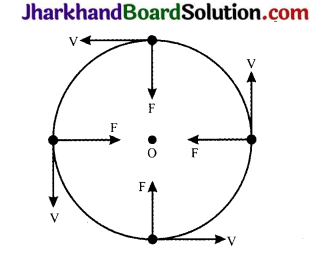
4. The figure given here shows that it is the centripetal force which continuously deflects a particle from its straight line path to make it move along a circle.
5. Example: The moon needs a centripetal force for its circular motion around the earth. This centripetal force is provided by the gravitational attraction exerted by the earth on the moon.

Question 2.
Show that the weight of an object on the moon is 1/6,h its weight on the earth. Given that the mass of the earth is 100 times the mass of the moon and its radius is 4 times that of the moon.
Answer:
Suppose, mass of the object = m
mass of the earth = M_e
mass of the moon = M_m
radius of the earth = R_e
radius of the moon = R_m
Then, M_e = 100 Mm and Re = 4Rm
Weight of an object of mass m on the earth is
We = the force with which the earth
attracts the object = G \(\frac{\mathrm{M}_{\mathrm{e}} \mathrm{m}}{\mathrm{R}_{\mathrm{e}}^{2}}\)
Weight of the object on the moon is
W_m = The force with which the moon
attracts the object = \( \mathrm{G} \frac{\mathrm{M}_{\mathrm{m}} \mathrm{m}}{\mathrm{R}_{\mathrm{m}}^{2}}\)
\(\frac{W_{m}}{W_{e}}\) = \(\frac{\left(G \frac{M_{m} m}{R_{m}^{2}}\right)}{\left(G \frac{M_{m} m}{R_{e}^{2}}\right)}\)
= \(\frac{M_{m}}{M_{e}} \times \frac{\left(R_{e}\right)^{2}}{\left(R_{m}\right)^{2}}\)
= \(\frac{\mathrm{M}_{\mathrm{m}}}{100 \mathrm{M}_{\mathrm{m}}} \times \frac{4 \mathrm{R}_{\mathrm{m}}^{2}}{\mathrm{R}_{\mathrm{m}}^{2}}\) = \(\frac{16}{100} \approx \frac{1}{6}\)
Thus, the weight of an object on the moon is about one – sixth of its weight on the earth.

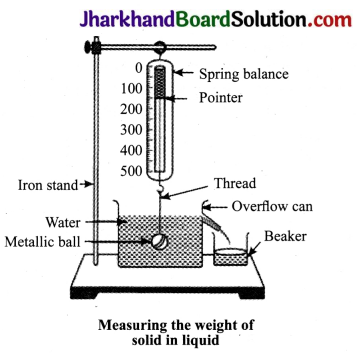
Question 3.
Briefly explain how can Archimedes’ principle be verified experimentally.
Answer:
According to Archimedes’ principle, when a body is immersed in a liquid, completely or partially, it loses its weight. The loss in weight is equal to the weight of liquid displaced by the body. The loss in weight of a body is due to the presence of upthrust which is equal to the weight of liquid displaced.
Thus, a Loss in weight = Weight of body in air – Weight of body immersed in water =
W W₁ = upthrust in water on the body = Weight of liquid displaced.

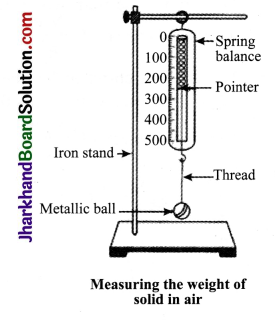
As shown in figure, measure the weight of a solid, say a metallic ball, in air using spring balance. Weigh the empty beakers using spring balance. Set the spring balance, overflow can with tap water and beaker. Now, allow the bob to immerse completely in water in overflow can. Note down the new position of the pointer of the spring balance.

This will give you the weight of the brass bob in tap water. It is found to be less than the weight of bob in air. Weigh the beaker containing displaced water which is collected from the overflow can while immersing the bob in it completely. It is observed that the loss in weight of the bob is equal to the weight of the water collected in the beaker, i.e., weight of the water displaced.

Question 4.
With the help of an activity, prove that the force acting on a lesser area exerts a larger pressure.
Answer:
Consider a block of wood kept on a tabletop. The mass of the wooden block is 5kg. Its dimensions are 30 cm × 20 cm × 10 cm.
Now, we have to find the pressure applied by the wooden block on the tabletop by keeping it vertically and horizontally.

The mass of the wooden block = 5kg
Weight of the wooden block applies a thrust on the tabletop.
Thrust = F = mg = 5kg × 9.8 m/s² = 49 N
(Case a) : When the wooden box is kept vertically with sides 20 cm × 10 cm,
Area of a side = length × breadth = 20 cm × 10 cm = 200 cm² = 0.02m²
Pressure = \(\frac{Thrust}{Area}\) = \(\frac{49 \mathrm{~N}}{0.02 \mathrm{~m}^{2}}\)
= 2450 N/m²

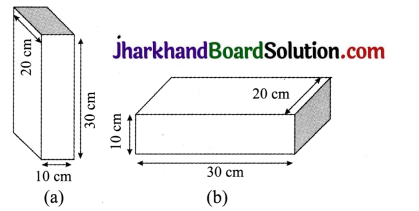
(Case b): When the block is kept horizontally with side 30 cm × 20 cm, Area = length × breadth = 30 cm × 20 cm = 600 cm² = 0.06 m²

Pressure = \(\frac{Thrust}{Area}\) = [/latex] \frac{49 \mathrm{~N}}{0.02 \mathrm{~m}^{2}}[/latex]
= 816.7 N/m²
The pressure exerted by the box in case (a) in more as compared to the pressure exerted in case (b). The area is reduced and the pressure exerted is more.
This shows that pressure ∝= \( \frac{1}{\text { Area }}\)
Hence, pressure will be larger if the area is reduced.

Analysing & Evaluating Questions

Question 5.
(a) A cube of side 5 cm is immersed in water and then in saturated salt solution. In which case it will experience a greater buoyant force. If each side of the cube is reduced to 4 cm and then immersed in water, what will be the effect on the buoyant force experienced by the cube as compared to the first case for water.

(b) A ball of weight 4 kg and density 4000 kg m³ is completely immersed in water of density 10³ kg m³. Find the force of buoyancy on it. (Given g = 10 ms^-2)
Answer:
(a) The cube will experience greater buoyant force in salt solution. When the side of the cube is reduced to 4 cm, it will experience lesser buoyant force as compared to the first case.
This is because the volume of water displaced by the smaller cube is lesser than that displaced by the original cube,

(b) Volume of water displaced by the ball = Volume of the ball = \(\frac{Mass}{Density}\)
= \(\frac{4 \mathrm{~kg}}{4000 \mathrm{~kg} \mathrm{~m}^{-3}}\) = 10^-3 m³
Weight of water displaced by the ball = Volume of water × Density × g
= 10^-3 m³ × 10³ kg m³ × 10 ms^-2 = 10 N
So, Buoyant force acting on the ball = Weight of water displaced = 10 N

Activity 1

• Take a piece of thread.
• Tie a small stone at one end. Hold the other end of the thread and whirl it round.
• Note the motion of the stone.
• Now release the thread.
• Again, note the direction of motion of the stone.
• Record your observations and draw conclusion about the direction of the stone.
  
• If thread is released when stone is here, stone goes straight towards A not towards B Top view A stone describing a circular path

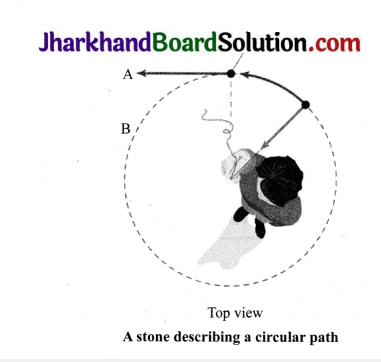
Observations

• The motion gets accelerated and stone moves in a circular path.
• When the thread is released, the stone makes a tangent to the circle and falls down.

ACTIVITY 2

• Take a sheet of paper and a stone. Drop them simultaneously from the first floor of a building.
• Observe whether both of them reach the ground simultaneously or not.

Observations

• We see that the paper reaches the ground a little later than the stone. This happens because of air resistance. The air offers resistance due to friction to the motion of the falling objects. The resistance offered by air to the paper is more than the resistance offered to the stone.
• If we do the experiment in a glass jar from which air has been sucked out, the paper and the stone would fall at the same rate.

ACTIVITY 3

• Take an empty plastic bottle. Close the mouth of the bottle with an airtight stopper. Put it in a bucket filled with water and observe.
• Push the bottle into the water and observe again. Try to push it further down.
• Now, release the bottle. Record your observations.
• Does the force due to the gravitational attraction of the earth act on this bottle? If so, why doesn’t the bottle stay immersed in water after it is released? How can you immerse the bottle in water?

Gravity

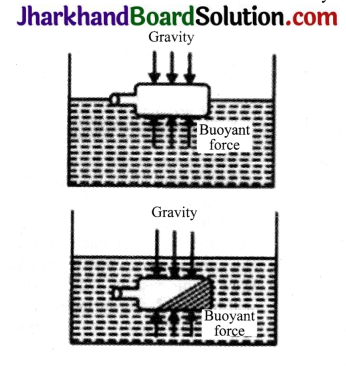
Observations

• The plastic bottle floats on water. When it is pushed deeper, the upward force on the bottle increases.
• When released, the bottle bounces back to the surface because the upthrust on the bottle was larger than the downward pull of gravity
• Take a piece of stone and tie it to one end of a rubber string or a spring balance.

ACTIVITY-4

• Take a piece of stone and tie it to one end of a rubber string or a spring balance.
  Thread
  
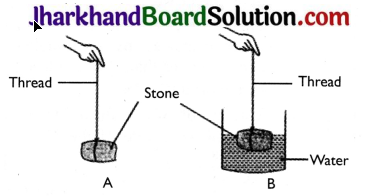
• Suspend the stone by holding the balance or the string as shown in the figure (A).
• Note the elongation of the string or the reading on the spring balance due to the weight of the stone.
• Now, slowly dip the stone in the water in a container as shown in Figure (B).
• Observe what happens to the elongation of the string or the reading on the balance.

Observations

• In fig. A, the elongation of the string is more.
• In fig. B, when the stone is dipped in water, the length of the string is reduced.
• The length of the string in case (B) decreases due to the upward force exerted by water on the stone called buoyant force.

Value Based Questions

Question 1.
Priya had a bad experience during the take off of the plane when she boarded it for the first time. Her friend assisted and helped her during the landing of plane. She told her to fasten the seat belt and involved her in gossip. Priya faced less problems while landing of the plane.
1. Why do we tie our seat belts in moving cars or during take off of the plane?
2. What is free fall?
3. What value of Priya’s friend is seen in this set?
Answer:

1. We tie our seat belts to remain intact on the seat so that our body does not fall forward.
2. When an object falls towards the earth under the gravitational force alone, we say that the object is in free fall.
3. Priya’s friend showed the value of concerned, sympathetic, responsible and caring friend.

Question 2.
A goldsmith measured the purity of gold by using a special measuring device. He told the customer that there was impurity present in gold ornament that he wanted to buy and was not 22 carat but 18 carat jewellery.
1. How can we find the purity of gold?
2. What is the unit of relative density?
3. What value of goldsmith is reflected in this act?
Answer:

1. The purity of gold can be obtained by knowing the density of the gold.
2. Relative density does not have any unit.
3. Goldsmith showed the value of honesty and trustworthiness.

JAC Class 9 Science Important Questions