Jharkhand Board JAC Class 9 Maths Important Questions Chapter 1 Number Systems Important Questions and Answers.
JAC Board Class 9th Maths Important Questions Chapter 1 Number Systems
Question 1.
Find 4 rational numbers between 2 and 3.
Solution :
Write 2 and 3 multiplying in numerator and denominator with (4 + 1).
i.e. 2 = \(\frac{2 \times 5}{1 \times 5}=\frac{10}{5}\)
or 3 = \(\frac{3 \times 5}{1 \times 5}=\frac{15}{5}\)
So, the four required rational numbers are \(\frac {11}{5}\), \(\frac {12}{5}\), \(\frac {13}{5}\), \(\frac {14}{5}\)
![]()
Question 2.
Find three rational numbers between a and b (a < b).
Solution :
a < b
⇒ a + a < b + a
⇒ 2a < a + b
⇒ a < \(\frac{a+b}{2}\)
Again, a < b
⇒ a + b < b + b
⇒ a + b < 2b
⇒ \(\frac{a+b}{2}\) < b
∴ a < \(\frac{a+b}{2}\) < b
i.e. \(\frac{a+b}{2}\) lies between a and b.
Hence, 1st rational number between a and b is \(\frac{a+b}{2}\)

Question 3.
Find 6 rational numbers between \(\frac {1}{3}\) and \(\frac {1}{2}\)
Solution :
LCM of 3 and 2 = 6
∴ \(\frac{1}{3}=\frac{2}{6}\) and \(\frac{1}{3}=\frac{2}{6}\)
Now, \(\frac{2}{6}=\frac{20}{60}\) and \(\frac{3}{6}=\frac{30}{60}\)
∴ \(\frac{21}{60}, \frac{22}{60}, \frac{23}{60}, \frac{24}{60}, \frac{25}{60}\) and \(\frac {26}{60}\) lie between \(\frac {1}{3}\) and \(\frac {1}{2}\).
Question 4.
Find 5 rational numbers between and \(\frac {3}{5}\) and \(\frac {4}{5}\)
Solution :
As \(\frac{3}{5}=\frac{3 \times 10}{5 \times 10}=\frac{30}{50}\) and
\(\frac{4}{5}=\frac{4 \times 10}{5 \times 10}=\frac{40}{50}\)
∴ 5 rationals between \(\frac {3}{5}\) and \(\frac {4}{5}\) are \(\frac{31}{50}, \frac{32}{50}, \frac{33}{50}, \frac{34}{50}\) and \(\frac {35}{50}\).
![]()
Question 5.
Find two irrational numbers between 2 and 2.5.
Solution :
\(\sqrt{2 \times 2.5}=\sqrt{5}\)
Since there is no rational number whose square is 5. So, \(\sqrt{5}\) is irrational.
Also, \(\sqrt{2 \times \sqrt{5}}\) is an irrational number.
∴ Irrational numbers between 2 and 2.5 are \(\sqrt{5}\) and \(\sqrt{3 \sqrt{5}}\).
Question 6.
Find two irrational numbers between \(\sqrt{2}\) and \(\sqrt{3}\).
Solution :
\(\sqrt{\sqrt{2} \times \sqrt{3}}=\sqrt{\sqrt{6}}=\sqrt[4]{6}\)
Irrational number between \(\sqrt{2}\) and \(\sqrt{3}\) are \(\sqrt[4]{6}, \sqrt{\sqrt{2} \times \sqrt[4]{6}}=\sqrt[4]{2} \times \sqrt[8]{6}\)
Question 7.
Find two irrational numbers between 0.12 and 0.13.
Solution :
0.1201001000100001…….,
0.12101001000100001……
![]()
Question 8.
Find two irrational numbers between 0.3010010001……. and 0.3030030003…..
Solution :
0.302020020002……, 0.302030030003….
Question 9.
Arrange \(\sqrt{2}\), \(\sqrt[3]{3}\) and \(\sqrt[4]{5}\) in ascending order.
Solution :
L.C.M. of 2, 3, 4 is 12.

Question 10.
Which is greater \(\sqrt{7}\) – \(\sqrt{3}\) or \(\sqrt{5}\) – 1 ?
Solution :
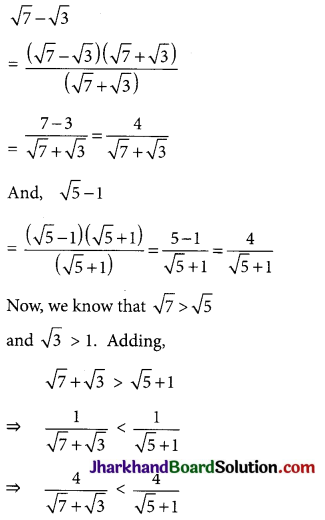
⇒ \(\sqrt{7}\) – \(\sqrt{3}\) < \(\sqrt{5}\) – 1 ⇒ \(\sqrt{5}\) – 1 > \(\sqrt{7}\) – \(\sqrt{3}\)
So, \(\sqrt{5}\) – 1 is greater.
![]()
Question 11.
Find the R.F. (rationalizing factor) of the following :
(i) \(\sqrt{12}\)
(ii) \(\sqrt{162}\)
(iii) \(\sqrt[3]{4}\)
(iv) \(\sqrt[3]{16}\)
(v) \(\sqrt[4]{162}\)
(vi) 2 + \(\sqrt{3}\)
(vii) 7 – 4\(\sqrt{3}\)
(vii) 3\(\sqrt{3}\) + 2\(\sqrt{2}\)
(ix) \(\sqrt[3]{3}\) + \(\sqrt[3]{2}\)
Solution :
(i) \(\sqrt{12}\)
First write its simplest form i.e. 2\(\sqrt{3}\).
Now R.F. of \(\sqrt{3}\) is \(\sqrt{3}\)
∴ R.F. of \(\sqrt{12}\) is \(\sqrt{3}\).
(ii) \(\sqrt{162}\)
Simplest form of \(\sqrt{162}\) is 9\(\sqrt{2}\).
R.F. of \(\sqrt{2}\) is \(\sqrt{2}\).
∴ R.F. of \(\sqrt{162}\) is \(\sqrt{2}\)
(iii) \(\sqrt[3]{4}\)
\(\sqrt[3]{4} \times \sqrt[3]{4^2}=\sqrt[3]{4^3}\) = 4
∴ R.F. of \(\sqrt[3]{4}\) is \(\sqrt[3]{4^2}\) or \(\sqrt[3]{16}\).
(iv) \(\sqrt[3]{16}\)
Simplest form of \(\sqrt[3]{16}\) is 2\(\sqrt[3]{2}\)
Now, R.F. of \(\sqrt[3]{2}\) is \(\sqrt[3]{2^2}\)
∴ R.F. of \(\sqrt[3]{16}\) is \(\sqrt[3]{2^2}\) or \(\sqrt[3]{4}\).
(v) \(\sqrt[4]{162}\)
Simplest form of \(\sqrt[4]{162}\) is 3\(\sqrt[4]{2}\)
Now, R.F. of \(\sqrt[4]{2}\) is \(\sqrt[4]{2^3}\) or \(\sqrt[4]{8}\)
R.E. of \(\sqrt[4]{162}\) is \(\sqrt[4]{2^3}\) or \(\sqrt[4]{8}\)
(vi) 2 + \(\sqrt{3}\)
As (2 + \(\sqrt{3}\))(2 – \(\sqrt{3}\)) = (2)2 – (\(\sqrt{3}\))2
= 4 – 3 = 1, which is rational.
∴ R.F. of 2 + \(\sqrt{3}\) is 2 – \(\sqrt{3}\).
(vii) 7 – 4\(\sqrt{3}\)
As (7 – 4\(\sqrt{3}\))(7 + 4\(\sqrt{3}\))
= (7)2 – (4\(\sqrt{3}\))2 = 49 – 48
= 1, which is rational
∴ R.E. of 7 – 4\(\sqrt{3}\) is 7 + 4\(\sqrt{3}\).
(viii) 3\(\sqrt{3}\) + 2\(\sqrt{2}\)
As (3\(\sqrt{3}\) + 2\(\sqrt{2}\))(3\(\sqrt{3}\) – 2\(\sqrt{2}\))
= (3\(\sqrt{3}\))2 – (2\(\sqrt{2}\))2 = 27 – 8
= 19, which is rational
∴ R.F. of 3\(\sqrt{3}\) + 2\(\sqrt{2}\) is 3\(\sqrt{3}\) – 2\(\sqrt{2}\)
(ix) \(\sqrt[3]{3}\) + \(\sqrt[3]{2}\)
As (\(\sqrt[3]{3}\) + \(\sqrt[3]{2}\))(\(\sqrt[3]{3^2}\) – \(\sqrt[3]{3}\) × \(\sqrt[3]{2}\) + \(\sqrt[3]{2^2}\))
= (\(\sqrt[3]{3}\))3 + (\(\sqrt[3]{2}\))3 = 3 + 2
= 5, which is rational
∴ R.F. of \(\sqrt[3]{3}\) + \(\sqrt[3]{2}\)
is (\(\sqrt[3]{3^2}\) – \(\sqrt[3]{3}\) × \(\sqrt[3]{2}\) + \(\sqrt[3]{2^2}\)).
Question 12.
Express the following surd with a rational denominator.
\(\frac{8}{\sqrt{15}+1-\sqrt{5}-\sqrt{3}}\)
Solution :
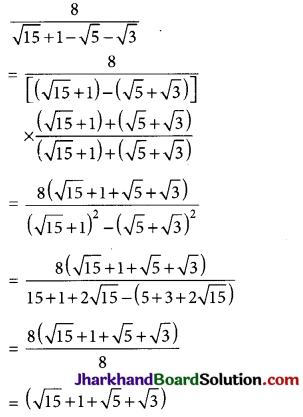
![]()
Question 13.
Rationalise the denominator of \(\frac{a^2}{\sqrt{a^2+b^2}+b}\)
Solution :

Question 14.
If \(\frac{3+2 \sqrt{2}}{3-\sqrt{2}}\) = a + b\(\sqrt{2}\), where a and b are rationals then find the values of a and b.
Solution :

Equating the rational and irrational parts, we get
a = \(\frac {13}{7}\) , b = \(\frac {9}{7}\)
Question 15.
If \(\sqrt{3}\) = 1.732, find the value of \(\frac{1}{\sqrt{3}-1}\).
Solution :
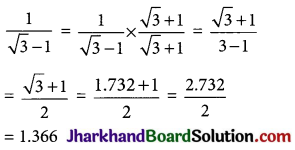
![]()
Question 16.
If \(\sqrt{5}\) = 2.236 and \(\sqrt{2}\) = 1.414, then evaluate : \(\frac{3}{\sqrt{5}+\sqrt{2}}+\frac{4}{\sqrt{5}-\sqrt{2}}\)
Solution :
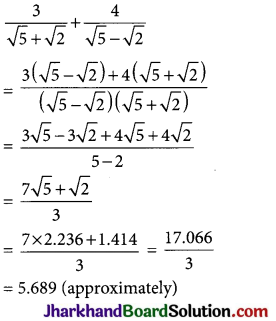
Question 17.
If x = \(\frac{1}{2+\sqrt{3}}\), find the value of x3 – x2 – 11x + 3.
Solution :
As, x = \(\frac{1}{2+\sqrt{3}}\) = 2 – \(\sqrt{3}\)
⇒ x – 2 = –\(\sqrt{3}\)
⇒ (x – 2)2 = (-\(\sqrt{3}\))2
[By Squaring both sides]
⇒ x2 + 4 – 4x = 3
⇒ x2 – 4x + 1 = 0
Now, x3 – x2 – 11x + 3
= x3 – 4x2 + x + 3x2 – 12x + 3
= x (x2 – 4x + 1) + 3 (x2 – 4x + 1)
= x(0) + 3 (0) = 0 + 0 = 0
Question 18.
If x = 3 – \(\sqrt{8}\) , find the value of x3 + \(\frac{1}{x^3}\).
Solution :

Question 19.
If x = 1 + 21/3 + 22/3, show that x3 – 3x2 – 3x – 1 = 0
Solution :
x = 1 + 21/3 + 22/3
⇒ x – 1 = (21/3 + 22/3)
⇒ (x – 1)3 = (21/3 + 22/3)3
⇒ (x – 1)3
⇒ (21/3)3 + (22/3)3 + 3.21/3 × 21/3(21/3 + 22/3)
⇒ (x – 1)3 = 2 + 22 + 3.21 (x – 1)
⇒ (x – 1)3 = 6 + 6(x – 1)
⇒ x3 – 3x2 + 3x – 1 = 6x
⇒ x3 – 3x2 – 3x – 1 = 0
![]()
Question 20.
Solve : \(\sqrt{x+3}+\sqrt{x-2}\) = 5
Solution :
⇒ \(\sqrt{x+3}+\sqrt{x-2}\) = 5
⇒ \(\sqrt{x+3}\) = 5 – \(\sqrt{x-2}\)
⇒ (\(\sqrt{x+3}\))2 = (5 – \(\sqrt{x-2}\))2
[By squaring both sides]
⇒ x + 3 = 25 + (x – 2) – 10\(\sqrt{x-2}\)
⇒ x + 3 = 25 + x – 2 – 10\(\sqrt{x-2}\)
⇒ 3 – 23 = – 10\(\sqrt{x-2}\)
⇒ – 20 = – 10\(\sqrt{x-2}\)
⇒ 2 = \(\sqrt{x-2}\)
⇒ x – 2 = 4 [By squaring both sides]
⇒ x = 6
Question 21.
If x = 1 + \(\sqrt{2}\) + \(\sqrt{3}\), prove that x4 – 4x3 – 4x2 + 16 – 8 = 0.
Solution :
x = 1 + \(\sqrt{2}\) + \(\sqrt{3}\)
⇒ x – 1 = \(\sqrt{2}\) + \(\sqrt{3}\)
⇒ (x – 1)2 = (\(\sqrt{2}\) + \(\sqrt{3}\))2
[By squaring both sides]
⇒ x2 + 1 – 2x = 2 + 3 + 2\(\sqrt{6}\)
⇒ x2 – 2x – 4 = 2\(\sqrt{6}\)
⇒ (x2 – 2x – 4)2 = (2\(\sqrt{6}\))2
⇒ x4 + 4x2 + 16 – 4x3 + 16x – 8x2 = 24
⇒ x4 – 4x3 – 4x2 + 16x + 16 – 24 = 0
⇒ x4 – 4x3 – 4x2 + 16x – 8 = 0
Question 22.
Evaluate each of the following:
(i) 52 × 54
(ii) 58 ÷ 53
(iii) (32)3
(iv) (\(\frac {11}{12}\))3
(v) (\(\frac {3}{4}\))-3
Solution :
Using the laws of indices, we have
(i) 52 × 54 = 52+4 = 56 = 15625
[∵ am × an = am+n]
(ii) 58 ÷ 53 = \(\frac{5^8}{5^3}\) = 58-3 = 55 = 3125
[∵ am ÷ an = am-n]
(iii) (32)3 = 32×3 = 36 = 729
[∵ (am)n = am×n]

![]()
Question 23.
Evaluate each of the following.
(i) (\(\frac {2}{11}\))4 × (\(\frac {11}{3}\))2 × (\(\frac {3}{2}\))3
(ii) (\(\frac {1}{2}\))5 × (\(\frac {-2}{3}\))4 × (\(\frac {3}{5}\))-1
(iii) 255 × 260 – 297 × 218
(iv) (\(\frac {2}{3}\))3 × (\(\frac {2}{5}\))-3 × (\(\frac {3}{5}\))2
Solution :
(i) We have,
(\(\frac {2}{11}\))4 × (\(\frac {11}{3}\))2 × (\(\frac {3}{2}\))3

Question 24.
Simplify :
(i) \(\frac{(25)^{3 / 2} \times(243)^{3 / 5}}{(16)^{5 / 4} \times(8)^{4 / 3}}\)
(ii) \(\frac{16 \times 2^{n+1}-4 \times 2^n}{16 \times 2^{n+2}-2 \times 2^{n+2}}\)
Solution :
We have
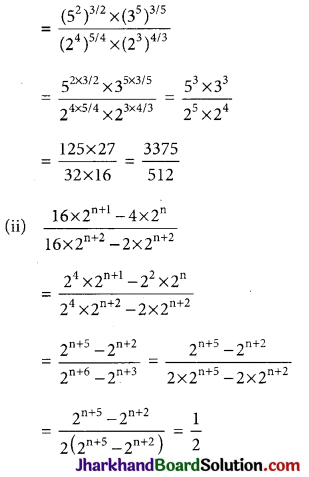
Question 25.
Simplify :
\(\left(\frac{81}{16}\right)^{-3 / 4} \times\left[\left(\frac{25}{9}\right)^{-3 / 2} \div\left(\frac{5}{2}\right)^{-3}\right]\)
Solution :
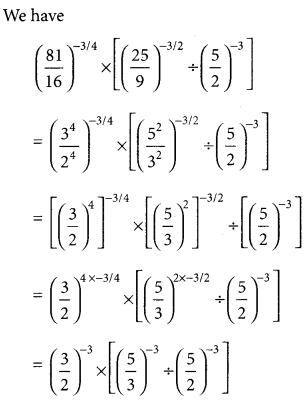

Multiple Choice Questions
Question 1.
If x = 3 + \(\sqrt{8}\) and y = 3 – \(\sqrt{8}\) then \(\frac{1}{x^2}+\frac{1}{y^2}\) =
(a) – 34
(b) 34
(c) 12\(\sqrt{8}\)
(d) – 12\(\sqrt{8}\)
Solution :
(b) 34
![]()
Question 2.
If \(\frac{3+\sqrt{7}}{3-\sqrt{7}}\) = a + b\(\sqrt{7}\) then (a, b) =
(a) (8, -3)
(b) (-8, -3)
(c) (-8, 3)
(d) (8, 3)
Solution :
(d) (8, 3)
Question 3.
Which of the following is an irrational number ?
(a) 0.24
(b) \(0 . \overline{24}\)
(c) 0.5777….
(d) 0.242242224…
Solution :
(d) 0.242242224…
Question 4.
If x = \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\) and y = 1, then value of \(\frac{x-y}{x-3 y}\) is :
(a) \(\frac{5}{\sqrt{5}-4}\)
(b) \(\frac{5}{\sqrt{6}+4}\)
(c) \(\frac{\sqrt{6}-4}{5}\)
(d) \(\frac{\sqrt{6}+4}{5}\)
Solution :
(d) \(\frac{\sqrt{6}+4}{5}\)
Question 5.
\(\sqrt{2}\) is a/an _________ number.
(a) natural
(b) whole
(c) irrational
(d) integer
Solution :
(c) irrational
![]()
Question 6.
The value of \(\sqrt[5]{(32)^{-3}}\) is:
(a) 1/8
(b) 1/16
(c) 1/32
(d) None
Solution :
(a) 1/8
Question 7.
If x = \(\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}\) and y = \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\) then value of x2 + xy + y2 is :
(a) 99
(b) 100
(c) 1
(d) 0
Solution :
(a) 99
Question 8.
Which of the following is not a rational number?
(a) 2 + \(\sqrt{3}\)
(b) – \(\frac {7}{11}\)
(c) 3.42
(d) \(0 .23 \overline{4}\)
Solution :
(a) 2 + \(\sqrt{3}\)
Question 9.
Which of the following is smallest?
(a) \(\sqrt[4]{5}\)
(b) \(\sqrt[5]{4}\)
(c) \(\sqrt{4}\)
(d) \(\sqrt{3}\)
Solution :
(b) \(\sqrt[5]{4}\)
![]()
Question 10.
The product of \(\sqrt{3}\) and \(\sqrt[3]{5}\) is:
(a) \(\sqrt[6]{375}\)
(b) \(\sqrt[6]{675}\)
(c) \(\sqrt[6]{575}\)
(d) \(\sqrt[6]{475}\)
Solution :
(b) \(\sqrt[6]{675}\)
Question 11.
The exponential form of \(\sqrt{\sqrt{2}} \times \sqrt{2} \times \sqrt{2}\) is :
(a) 21/16
(b) 83/4
(c) 23/4
(d) 81/2
Solution :
(c) 23/4
Question 12.
The value of x, if 5x-3 × 32x-8 = 225, is:
(a) 1
(b) 2
(c) 3
(d) 5
Solution :
(d) 5
Question 13.
If 25x ÷ 2x = \(\sqrt[5]{2^{20}}\) then x =
(a) 0
(b) – 1
(c) \(\frac {1}{2}\)
(d) 1
Solution :
(d) 1
![]()
Question 14.
If 10x = \(3 . \overline{3}\) = 3 + x, then x =
(a) \(\frac {1}{9}\)
(b) \(\frac {1}{3}\)
(c) 3
(d) 9
Solution :
(b) \(\frac {1}{3}\)
Question 15.
A rational number between \(\frac {1}{7}\) and \(\frac {1}{3}\) is
(a) \(\frac {29}{210}\)
(b) \(\frac {50}{210}\)
(c) \(\frac {81}{210}\)
(d) \(\frac {93}{210}\)
Solution :
(b) \(\frac {50}{210}\)