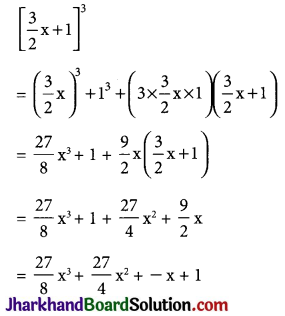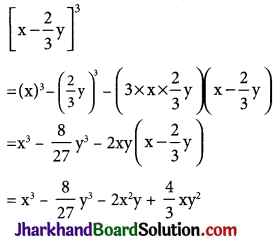Month: September 2024

Jharkhand Board JAC Class 9 Maths Solutions Chapter 3 Coordinate Geometry Ex 3.3 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 3 Coordinate Geometry Ex 3.3

Page-65

Question 1.
In which quadrant or on which axis do each of the points (-2, 4), (3, -1), (-1, 0), (1,2) and (-3, -5) lie? Verify your answer by locating them on the Cartesian plane.
Answer:

(-2, 4) → Second quadrant
(3,-1) → Fourth quadrant
(-1,0) → x-axis
(1,2) → First quadrant
(-3, -5)→ Third quadrant

Question 2.
Plot the points (x, y) given in the following table on the plane, choosing suitable units of distance on the axes.

x	-2	-1	0	1	3
y	8	7	-1.25	3	-1

Ans. Points (x, y) on the plane, 1 unit = 1 cm

Jharkhand Board JAC Class 9 Maths Solutions Chapter 14 Statistics Ex 14.2 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 14 Statistics Ex 14.2

Page-245

Question 1.
The blood groups of 30 students of Class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
Represent this data in the form of a frequency distribution table. Which is the most common, and which is the rarest, blood group among these students?
Answer:
The frequency means the number of students having same blood group. We will represent the data in table:

Blood Group	Number of Students (Frequency)
A	9
B	6
O	12
AB	3
Total	30

Most common Blood Group (Highest frequency): O
Rarest Blood Group (Lowest frequency): AB

Question 2.
The distance (in km) of 40 engineers from their residence to their place of work w ere found as follows:

5	3	10	20	25
11	13	7	12	31
19	10	12	17	18
11	32	17	16	2
7	9	7	8	3
5	12	15	18	3
12	14	2	9	6
15	15	7	6	12

Construct a grouped frequency distribution table with class size 5 for the data given above taking the first interval as 0-5 (5 not included). What main features do you observe from this tabular representation?
Answer:
The given data is very large. So, we con-struct a group frequency of class size 5. Therefore, class interval will be 0-5, 5-10, 10-15, 15-20 and so on. The data is represented in the table as:

The classes in the table are not overlap¬ping. Also, 36 out of 40 engineers have their house below 7. 20 km of distance.

Question 3.
The relative humidity (in %) of a certain city for follows: a month of 30 days was as

98.1	98.6	99.2	90.3	86.5
95.3	92.9	96.3	94.2	95.1
89.2	92.3	97.1	93.5	92.7
95.1	97.2	93.3	95.2	97.3
96.2	92.1	84.9	90.2	95.7
98.3	97.3	96.1	92.1	89

(i) Construct a grouped frequency distribution table with classes 84 – 86, 86 – 88, etc.
(ii) Which month or season do you think this data is about?
(iii) What is the range of this data?
Answer:
(i) The given data is very large. So, we construct a group frequency of class size 2. Therefore, class interval will be 84-86, 86-88, 88-90, 90-92 and so on. The data is represented in the table as below:

Relative humidity (in %)	Frequency
84-86	1
86-88	1
88-90	2
90-92	2
84-86	1
86-88	1
88-90	2
90-92	2
92-94	7
94-96	6
96-98	7
98-100	4
Total	30

(ii) The humidity is very high in the data which is observed during rainy season. So, it must be rainy season.
(iii) Range of data = Maximum value of data – Minimum value of data = 99.2 – 84.9 = 14.3%

Question 4.
The heights of 50 students, measured to the nearest centimetres, have been found to be as follows:

161	150	154	165	168
161	154	162	150	151
162	164	171	165	158
154	156	172	160	170
153	159	161	170	162
165	166	168	165	164
154	152	153	156	158
162	160	161	173	166
161	159	162	167	168
159	158	153	154	159

(i) Represent the data given above by a grouped frequency distribution table, taking the class intervals as 150-155,155-160, etc. soon.
(ii) What can you conclude about their heights from the table?
Answer:
(i) The data with class interval 150-155, 155-160 and so on is represented in the table as:

Height (in cm)	No. of Students (Frequency)
150-155	12
155-160	9
160-165	14
165-170	10
170-175	5
Total	50

(ii) From the given data, it can be concluded that 35 students i.e. more than 50% are shorter than 165 cm.

Question 5.
A study was conducted to find out the concentration of sulphur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows:

(i) Make a grouped frequency distribution table for this data with class intervals as 0.00-0.04, 0.04-0.08, and so on.
(ii) For how many days, was the concentration of sulphur dioxide more than 0.11 parts per million?
Answer:
(i) The data with class interval 0.00 – 0.04, 0.04 – 0.08 and so on is represented in the table as:

Concentration of sulphur dioxide in air (in ppm)	Frequency
0.00 – 0.04	4
0.04 – 0.08	9
0.08 – 0.12	9
0.12-0.16	2
0.16-0.20	4
0.20 – 0.24	2
Total	30

(ii) 2 + 4 + 2 = 8 days have the concentration of sulphur dioxide more than 0.11 parts per million.

Page-246

Question 6.
Three coins were tossed 30 times simultaneously. Each time the number of heads occurring was noted down as follows:

Prepare a frequency distribution table for the data given above.
Answer:
The frequency distribution table for the data given above can be prepared as follows:

Number of Heads	Frequency
0	6
1	10
2	9
3	5
Total	30

Question 7.
The value of π upto 50 decimal places is given below:
3.14159265358979323846264338327950288419716939937510
(i) Make a frequency distribution of the digits from 0 to 9 after the decimal point.
(ii) What are the most and the least frequently occurring digits?
Answer:
(i) The frequency is given as follows:

Digits	Frequency
0	2
1	5
2	5
3	8
4	4
5	5
6	4
7	4
8	5
9	8
Total	50

(ii) The digit having the least frequency occurs the least and the digit with highest frequency occurs the most. 0 has frequency 2 and thus occurs least frequently while 3 and 9 have frequency 8 and thus occur most frequently.

Question 8.
Thirty children were asked about the number of hours they watched TV programmes in the previous week. The results were found as follows:

(i) Make a grouped frequency distribution table for this data, taking class width 5 and one of the class intervals as 5-10.
(ii) How many children watched television for 15 or more hours a week?
Answer:
(i) The distribution table for the given data, taking class width 5 and one of the class intervals as 5-10 is as follows:

Number of Hours	Frequency
0 – 5	10
5 – 10	13
10 – 15	5
15 – 20	2
Total	30

(ii) We observed from the given table that 2 children watched television for 15 or more hours a week.

Question 9.
A company manufactures car batteries of a particular type. The lives (in years) of 40 such batteries were recorded as follows:

Construct a grouped frequency distribution table for this data, using class intervals of size 0.5 starting from the interval 2-2.5.
Answer:
A grouped frequency distribution table using class intervals of size 0.5 starting from the interval 2-2.5 is constructed.

Lives of batteries (in years)	No. of batteries (Frequency)
2 – 2.5	2
2.5 – 3	6
3 – 3.5	14
3.5 – 4	11
4 – 4.5	4
4.5 – 5	3
Total	40

Jharkhand Board JAC Class 9 Maths Solutions Chapter 14 Statistics Ex 14.1 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 14 Statistics Ex 14.1

Page-239

Question 1.
Give five examples of data that you can collect from your day-to-day life.
Answer:
Five examples from day-to-day life:
(i) Daily expenditures of household.
(ii) Amount of rainfall.
(iii) Bill of electricity.
(iv) Poll or survey results.
(v) Marks obtained by students.

Question 2.
Classify the data in Q. 1 above as primary or secondary data.
Answer:
Primary Data: (i), (iii) and (v)
Secondary Data: (ii) and (iv)

Jharkhand Board JAC Class 9 Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.2 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.2

Page-159

Question 1.
In Fig, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

Answer:
Given: AB = CD = 16 cm (Opposite sides of a parallelogram)
CF = 10 cm and AE = 8 cm
Now, Area of parallelogram = Base × Altitude = CD × AE = AD × CF
⇒ 16 × 8 = AD × 10
⇒ AD = \(\frac{128}{10}\) cm
⇒ AD = 12.8 cm

Question 2.
If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that
ar(EFGH) = \(\frac{1}{2}\) ar(ABCD)

Answer:
Given: E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD.
To Prove: ar (EFGH) = \(\frac{1}{2}\) ar(ABCD)
Construction: H and F are joined.
Proof: AD || BC and AD = BC (Opposite sides of a Parallelogram)
⇒ AH || BF and \(\frac{1}{2}\) AD = \(\frac{1}{2}\) BC
⇒ AH || BF and AH = BF (Hand Fare mid points)
Thus, ABFH is a parallelogram.
[Since a pair of lines is equal and parallel]
⇒ AB || HF

Now, AEFH and ||^gm ABFH lie on the same base FH and between the same parallel lines AB and HF.
∴ area of AEFH = \(\frac{1}{2}\) area of ABFH ……..(i)
AD || BC and AD = BC [Opposite sides of a parallelogram ABCD]
⇒ DH CF and \(\frac{1}{2}\) AD = \(\frac{1}{2}\) BC
⇒ DH || CFand DH = CF [As Hand Fare mid-point of AD and BC respectively]
⇒ CDHF is a parallelogram [Since a pair of opposite sides is equal and parallel]
Now, AFGH and parallelogram CDHF lie an same base HF and between the same parallel lines HF and CD
∴ area of AFGH = \(\frac{1}{2}\) area of CDHF ……..(ii)

Adding (i) and (ii),
area of AEFH + area of AGHF
= \(\frac{1}{2}\) area of ABFH + \(\frac{1}{2}\) area of HFCD
⇒ area of EFGH = \(\frac{1}{2}\) area of ABCD
⇒ ar (EFGH) = \(\frac{1}{2}\) ar(ABCD)

Question 3.
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB) = ar(BQC).

Answer:
∆APB and ||^gm ABCD are on the same base AB and between same parallels AB and DC.
Therefore, (∆APB) = ar(||^gm ABCD) ……….(i)
Similarly,
ar(∆BQC) = \(\frac{1}{2}\) ar(||^gm ∆BCD) ………(ii)
From (i) and (ii),
we have, ar(∆APB) = ar(∆BQC)

Question 4.
In Fig, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(∆APB) + ar(∆PCD) = \(\frac{1}{2}\) ar(||^gm ABCD)
(ii) ar(∆APD) + ar(∆PBC) = ar(∆APB) + ar(∆PCD)
[Hint: Through P, draw a line parallel to AB.]

Answer:
Img 5
(i) Draw a line GH is drawn parallel to AB passing through P.
In parallelogram ABCD
AB || GH (by construction) …………(i)
AD || BC (Opposite sides of parallelogram ABCD)
⇒ AG || BH …(ii)
From equations (i) and (ii),
ABHG is a parallelogram.

Now, ∆APB and parallelogram ABHG are lying on the same base AB and between the same parallel lines AB and GH.
∴ ar(∆APB) = \(\frac{1}{2}\) ar(∆BHG) …(iii)
Now, AB || GH (By construction)
AB || CD (Opposite sides of parallelogram)
⇒ CD || GH (Lines parallel to same line are parallel to each other)
Also, CH || GD (as AD || BC)
∴ CDGH is a parallelogram.

Now, APCD and parallelogram CDGH are lying on the same base CD and between the same parallel lines CD and GH.
ar(APCD) = \(\frac{1}{2}\) ar(CDGH)
Adding equations (iii) and (iv),
ar(AAPB) + ar(APCD) = \(\frac{1}{2}\) [ar(ABHG) + ar(CDGH)]
⇒ ar(AAPB) + ar(APCD) = \(\frac{1}{2}\) ar(||^gm ABCD).

(ii) A line EF is drawn parallel to AD passing through P.
In a parallelogram ABCD
AD || EF (by construction) ……..(v)
Also, AB || CD
⇒ AE || DF ………..(vi)
From equations (v) and (vi), AEFD is a parallelogram.

Now, ∆ APD and parallelogram AEFD are lying on the same base AD and between the same parallel lines AD and EF.
ar(∆APD) = \(\frac{1}{2}\) ar(AEFD) ……(vii)
Now, AD || EF (By construction) AD||BC (Opposite sides of parallelogram)
⇒ BC || EF
Also, AB || CD
⇒ BE || CF
BCFE is a parallelogram.

Also, ∆PBC and parallelogram BCFE are lying on the same base BC and between the same parallel lines BC and EF.
∴ ar(∆PBC) = \(\frac{1}{2}\) ar(BCFE) …(viii)
Adding equations (vii) and (viii),
ar(∆APD) + ar(∆PBC)
= \(\frac{1}{2}\) [ar(AEFD) + ar(BCFE)]
= \(\frac{1}{2}\) ar(ABCD)
⇒ ar(∆APD) + ar(∆PBC) = ar(∆APB) + ar(∆PCD)

Question 5.
In Fig, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar(PQRS) = ar(ABRS)
(ii) ar(∆AXS) = \(\frac{1}{2}\) ar(PQRS)

Answer:
(i) Parallelogram PQRS and ABRS lie on the same base SR and between the same parallel lines SR and PB.
∴ ar(PQRS) = ar(ABRS) …………(i)

(ii) ∆AXS and parallelogram ABRS are lying on the same base AS and between the same parallel lines AS and BR.
ar(∆AXS) = \(\frac{1}{2}\) ar(ABRS) …(ii)
From (i) and (ii),
ar(∆AXS) = \(\frac{1}{2}\) ar(PQRS)

Page-160

Question 6.
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In howT many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow7 wheat and pulses in equal portions of the field separately. How should she do it?

Answer:
The field is divided into three parts. The three parts are in the shape of triangles.
These are ∆PSA, ∆PAQ and ∆QAR.
Area of ∆PSA + ∆PAQ + ∆QAR = Area of PQRS …….(i)
Area of APAQ = \(\frac{1}{2}\) area of PQRS ……….(ii)
(v Triangle and parallelogram are on the same base and between the same parallel lines.)
From (i) and (ii),
Area of ∆PSA + Area of ∆QAR = \(\frac{1}{2}\) area of PQRS … (iii)
Clearly from (ii) and (iii),
Farmer must sow wheat or pulses in ∆PAQ or in both ∆PSA and ∆QAR.

Jharkhand Board JAC Class 9 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.9 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.9

Question 1.
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see Fig. 13.31). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm² and the rate of painting is 10 paise per cm², find the total expenses required for polishing and painting the surface of the bookshelf.

Solution:
Let L, B, H be the external length, breadth and height of the bookshelf
Here L= 110 cm, B= 85 cm, H = 25 cm
let l, b, h be the internal length, breadth and height of the bookshelf

Thickness of the plank = 5cm
l = (110 – 5 – 5) cm = 100cm
b = (85 – 5 – 5) cm = 75cm,
h = (25 – 5) cm = 20 cm

External surface area of the bookshelf = LB + 2 (BH + RL)
= 110 × 85 cm² + 2(85 × 25 + 25 × 110) cm²
= (9350 ÷ 9750) cm² = 19100 cm²

Surface area of the border
= (4 × 75 × 5 + 110 × 5 × 2) cm²
= (1500 + 1100) cm² =2600 cm²

∴ Total surface area to be polished
= (19100 + 2600) cm²
= 21700 cm²

Rate of polishing per cm² = 20 paise = ₹ \(\frac{20}{100}\)

∴ Cost of polishing the outer surface = ₹ \(\frac{21700 \times 20}{100}\) = ₹ 4340 ……(i)

Area to be painted = lb + 2 (bh + hl)
= 100 × 75 + 2 (75 × 20 + 20 × 100)
= 7500 + 7000
= 14500 cm²

Surface area of two rack = 4 × 75 × 20 = 6000 cm²

Inner Surface area covered by rack = (75 × 5 × 2 + 20 × 5 × 4)
= 1150 cm²

Total Surface area to be painted = 14500 + 6000 – 1150 = 19350 cm²

Cost of painting the inner surface at the rate of 10 paise per cm²
= ₹ \(\frac{19350 \times 10}{100}\) = ₹ 1935

Form (i) and (ii), we have
Total expenses required for polished and painting the surface of the bookshelf.
= ₹ 4340 + ₹ 1935 = ₹ 6275

Page-237

Question 2.
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in Fig. 13.32. Eight such spheres are used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm² and black paint costs 5 paise per cm².

Solution:
Let R be the radius of the sphere and R, H be the radius and height of cylinder.
Radius of sphere (R) = \(\frac{21}{2}\) = 10.5 cm
Surface area of a sphere = 4πr²
= 4 × \(\frac{22}{7}\) × 10.5 × 10.5 cm²

Area of the top of the cylinder (support) = πR²
= π(1.5)² = cm²
= 7.07 cm²

Area of the sphere to be painted silver = (1386 – 7.07) cm²
= 1378. 93 cm²

Cost of silver paint per cm² = 25 paise

Cost of painting spheres = ₹ \(\frac{8 \times 1387.93 \times 25}{100}\)
= ₹ 2757.86 (approx.)

Curved surface area of a cylinder (support) = 2πRH
= 2 × \(\frac{22}{7}\) × 1.5 × 7 cm²

Cost of black paint per cm² = 5 paise

Curved surface area of 8 supports = 8 × 2 × \(\frac{22}{7}\) × 1.5 × 7 cm²

Cost of painting the supports
= ₹ 8 × 2 × \(\frac{22}{7}\) × 1.5 × 7 × \(\frac{5}{100}\)
= ₹ 26.40

Total cost = ₹ (2757.86 + 26.40)
= ₹ 2784.26.

Question 3.
The diameter of a sphere is decreased by 25%. By what percent does its curved surface area decrease?
Solution:

Let the diameter of sphere be 2r.
Then, Radius of the sphere =r
Surface area of sphere = 4πr² …..(i)
New diameter of the sphere = 2r – 2r × \(\frac{25}{100}\) = \(\frac{3r}{2}\)

New radius of the sphere = \(\frac{3r}{4}\)

Surface area of the new sphere
= \(=4 \pi\left(\frac{3 r}{4}\right)^2=\frac{9 \pi r^2}{4}\)

Decrease in surface area = 4πr² – \(\frac{9 \pi r^2}{4}\) = \(\frac{7 \pi r^2}{4}\)

Percent decrease

Hence, the surface area decrease by 43.75%.

Jharkhand Board JAC Class 9 Maths Solutions Chapter 6 Lines and Angles Ex 6.1 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 6 Lines and Angles Ex 6.1

Page-96

Question 1.
In Fig, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.

Answer:
Given,
∠AOC + ∠BOE = 70° and ∠BOD = 40°
∠AOC + ∠BOE + ∠COE = 180° (Forms a straight line)
⇒ 70° + ∠COE = 180°
⇒ ∠COE = 110°
∴ Reflex ∠COE = 360° – ∠COE = 360°- 110° = 250°
Also, ∠COE + ∠BOD + ∠BOE = 180° (Forms a straight line)
⇒ 110° + 40° + ∠BOE = 180°
⇒ 150° + ∠BOE = 180°
⇒ ∠BOE = 30°

Page-97

Question 2.
In Fig, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.

Answer:
Given, ∠POY = 90° and a : b = 2 : 3
∠POY + a + b = 180°
⇒ 90° + a + b = 180°
⇒ a + b = 90°

Let a be 2x and b be 3x.
∴ 2x + 3x = 90°
⇒ 5x = 90°
⇒ x = 18°
∴ a = 2 × 18° = 36° and b = 3 × 18° = 54°
Also, b + c = 180° (Linear Pair)
⇒ 54° + c = 180°
⇒ c = 126°

Question 3.
In Fig, if ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.

Answer:
Given: ∠PQR = ∠PRQ
To prove: ∠PQS = ∠PRT
Proof: ∠PQR + ∠PQS = 180° (Linear Pair)
⇒ ∠PQS = 180° – ∠PQR …….(i)
also, ∠PRQ + ∠PRT = 180° (Linear Pair)
⇒ ∠PRT = 180°- ∠PRQ
∠PRT = 180° – ∠PQR (∠PQR = ∠PRQ)…(ii)
From (i) and (ii)
∠PQS = ∠PRT = 180° – ∠PQR
Therefore, ∠PQS = ∠PRT

Question 4.
In Fig, if x + y = w + z, then prove that AB is a line.

Answer:
Given: x + y = w + z
To prove: AB is a line or x + y = 180° (linear pair)
Proof: x + y + w + z = 360° (Angles around a point)
⇒ (x + y) + (x + y) = 360° (Given x + y = w + z)
⇒ 2(x + y) = 360°
⇒ (x + y) = 180°
Hence, x + y makes a linear pair. Therefore, AB is a straight line.

Question 5.
In Fig, if PQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR.
Prove that ∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS).

Answer:
Given: OR is perpendicular to line PQ
To prove: ∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS).
Proof: ∠POR = ∠ROQ = 90° (Perpendicular)
∠QOS=∠ROQ+∠ROS=90°+∠ROS ……(i)
∠POS = ∠POR – ∠ROS = 90° – ∠ROS …….(ii)

Subtracting (ii) from (i)
∠QOS – ∠POS = (90° + ∠ROS) – (90° – ∠ROS)
⇒ ∠QOS – ∠POS = 90° + ∠ROS – 90° + ∠ROS
⇒ ∠QOS – ∠POS = 2 ∠ROS
⇒ ∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS)
Hence, proved.

Question 6.
It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.

Answer:
Given ∠XYZ = 64°
YQ bisects ∠YP
∠XYZ + ∠ZYP = 180° (Linear Pair)
⇒ 64° + ∠ZYP = 180°
⇒ ∠ZYP = 116°
Also, ∠ZYP = ∠ZYQ + ∠QYP
∠ZYQ = ∠QYP (YQ bisects ZYP)
⇒ ∠ZYP = 2 ∠ZYQ
⇒ 2 ∠ZYQ =116°
⇒ ∠ZYQ = 58° = ∠QYP
Now, ∠XYQ = ∠XYZ + ∠ZYQ
⇒ ∠XYQ = 64° + 58°
⇒ ∠XYQ = 122°
Also, reflex ∠QYP = 180° + ∠XYQ
= 180° + 122° = 302°

Jharkhand Board JAC Class 9 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.8 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.8

Question 1.
Find the volume of a sphere whose radius is :
(i) 7 cm
(ii) 0.63 m.
Solution:
(i) Radius of the sphere (r) = 7 cm
Therefore, Volume of sphere = \(\frac{4}{3}\)πr³
= \(\frac{4312}{3}\) cm³.

(ii) Radius of the sphere (r) = 0.63 m
∴ Volume of the sphere = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times 0.63 \times 0.63 \times 0.63\) m³
= 1.05 m³

Question 2.
Find the amount of water displaced by a solid spherical ball of diameter :
(i) 28 cm
(ii) 0.21 m.
Solution:
(i) Diameter of spherical ball = 28 cm
Radius (r) = \(\frac{28}{2}\) cm = 14 cm

Amount of water displaced by spherical ball = Volume of spherical ball
= \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7} \times 14 \times 14 \times 14\) cm³
= \(\frac{34496}{3}\) cm³

(ii) Diameter of spherical ball = 0.21 m
∴ Radius (r) = \(\frac{0.21}{2}\) = 0.105 m

Amount of water displaced by spherical ball = Volume of spherical ball
= \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7}\) × 0.105 × 0.105 × 0.105 m³
= 0.004851 m³

Question 3.
The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm³?
Solution:
Radius (r) = \(\frac{4.2}{2}\) = 2.1 cm
Volume of spherical ball = \(\frac{4}{3}\)πr³
= 38.808 cm³

Density of the metal is 8.9 g per cm³
mass of the ball = (38.808 × 8.9) g
= 345.3912 g

Question 4.
The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
Solution:
Let the diameter of the moon be r.
Radius of the moon = \(\frac{r}{2}\)
Diameter of the earth = 4r
Radius (R) = \(\frac{4r}{2}\) = 2r

Volume of the earth = v = \(\frac{4}{3}\)π\(\frac{r}{2}\)³
8v = \(\frac{4}{3}\)πr³ × \(\frac{1}{83}\) ……(i)

Volume of the earth = V = \(\frac{4}{3}\)π(2r)³
= \(\frac{4}{3}\)π(r)³ × 8
= \(\frac{V}{8}\) = \(\frac{4}{3}\)πr³ ………(ii)

From (i) and (ii), we have
8v = \(\frac{V}{8}\)
v = \(\frac{1}{64}\) V
Thus, the volume of the moon is of \(\frac{1}{64}\) the volume of the earth.

Question 5.
How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold.
Solution:
Diameter of hemispherical bowl = 10.5 cm
Radius (r) = \(\frac{10.5}{2}\) = 5.25 cm

Volume of the bowl = \(\frac{2}{3} \pi r^3\)
= \(\frac{2}{3} \times \frac{22}{7} \times 5.25 \times 5.25 \times 5.25\) cm³
= 303.1875 cm³

Litres of milk bowl can hold = \(\frac{303.1875}{1000}\)
= 0.3031875 litres (approx.)

Question 6.
A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
Solution:
Inner radius = r = 1 m
External radius = R = (1 + 0.01) m = 1.01 m

Volume of the iron used = External volume – Internal volume
= \(\frac{2}{3}\)πR³ – \(\frac{2}{3}\)πr³
= \(\frac{2}{3}\)π[R³ – r³]
= \(\frac{2}{3} \times \frac{22}{7}\)[(1.01)³ – (1)³] m³
= \(\frac{44}{21}\)(1.030301 – 1) m³
= \(\frac{44}{21}\) × 0.030301 m³
= 0·06348 m³ (approx.)

Question 7.
Find the volume of a sphere whose surface area is 154 cm².
Solution:
Let r cm be the radius of sphere.
Surface area of the sphere = 154 cm²
⇒ 4πr² = 154
⇒ 4 × \(\frac{22}{7}\) × r² = 154
⇒ r² = \(\frac{(154×7)}{(4×22)}\) = 12.25
⇒ r = 3.5 cm

Volume = \(\frac{4}{3} \pi r^3\)
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 3.5 × 3.5 × 3.5 cm³
= \(\frac{539}{3}\) cm³.

Question 8.
A dome of a building is in the form of a hemisphere. From inside, it was white washed at the cost of ₹ 498.96. If the cost of the white-washing is ₹ 2.00 per square metre, find the :
(i) inside surface area of the dome,
(ii) volume of the air inside the dome.
Solution:
(i) Inside surface area of the dome = Total cost of white washed/Rate of white washed per square metre
= \(\frac{498.96}{2.00}\) m² = 249.48 m²

(ii) Let r be the radius of the dome.
Surface area = 2πr²
⇒ 2 × \(\frac{22}{7}\) × r² = 249.48
⇒ r² = \(\frac{249.48 \times 7}{22 \times 2}\) = 39.69
⇒ r² = 39.69
⇒ r = 6.3 m.

Volume of the air inside the dome = Volume of the dome
= \(\frac{2}{3}\)πr³
= \(\frac{2}{3} \times \frac{22}{7}\) × 6.3 × 6.3 × 6.3
= 523.9 m³ (approx.)

Question 9.
Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S’. Find the :
(i) radius r’ of the new sphere,
(ii) radio of S and S’.
Solution:
Volume of 27 solid spheres of radius
r = 27 × \(\frac{4}{3}\)πr³

Volume of the new sphere of radius
r’ = \(\frac{4}{3} \pi r^{\prime} 3\)
⇒ \(\frac{4}{3} \pi r^{\prime} 3=27 \times \frac{4}{3} \pi r^3\)
⇒ \(r^{\prime 3}=\frac{27 \times \frac{4}{3} \pi r^3}{\frac{4}{3} \pi}\)
⇒ r’³ = 27r³ = (3r)³
⇒ r’= 3r

(ii) Required ratio = S’ = \(\frac{4 \pi r^2}{4 \pi r^{\prime 2}}\)
= \(\frac{r^2}{(3 r)^2}=\frac{r^2}{9 r^2}=\frac{1}{9}\) = 1 : 9

Question 10.
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm³) is needed to fill this capsule?
Solution:
Diameter of spherical capsule = 3.5 mm
Radius (r)= \(\frac{3.5}{2}\) mm = 1.75 mm

Medicine needed for its filling = Volume of spherical capsule = \(\frac{4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7}\) × 1.75 × 1.75 × 1.75 mm³
= 22.46 mm³ (approx.)

Jharkhand Board JAC Class 9 Maths Solutions Chapter 1 Number Systems Ex 1.4 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 1 Number Systems Exercise 1.4

Question 1.
Visualise 3.765 on the number line using successive magnification.
Answer:

Question 2.
Visualize 4.26 on the number line, up to 4 decimal places.
Answer:
\(4 . \overline{26}\) = 4.2626…

Jharkhand Board JAC Class 9 Maths Solutions Chapter 3 Coordinate Geometry Ex 3.2 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 3 Coordinate Geometry Ex 3.2

Page – 61

Question 1.
Write the answer of each of the following questions:
(i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?
(ii) What is the name of each part of the plane formed by these two lines?
(iii) Write the name of the point where these two lines intersect.
Answer:
(i) The names of horizontal line and vertical line drawn to determine the position of any point in the Cartesian plane are x-axis and y-axis respectively.
(ii) The name of each part of the plane formed by these two lines x-axis and y-axis is quadrant.
(iii) The point where these two lines intersect is called origin.

Question 2.
See Fig., and write the following:

(i) The coordinates of B.
(ii) The coordinates of C.
(iii) The point identified by the coordinates (-3, -5).
(iv) The point identified by the coordinates (2, -4).
(v) The abscissa of the point D.
(vi) The ordinate of the point H.
(vii) The coordinates of the point L.
(viii)The coordinates of the point M.
Answer:
(i) The coordinates of B are (-5, 2).
(ii) The coordinates of C are (5, -5).
(iii) The point identified by the coordinates (-3, -5) is E.
(iv) The point identified by the coordinates (2,-4) is G.
(v) Abscissa means x-coordinate of a point. So, abscissa of the point D is 6.
(vi) Ordinate means y-coordinate of a point. So, ordinate of point H is -3.
(vii) The coordinates of the point L are (0, 5).
(viii) The coordinates of the point M are (-3,0).

Jharkhand Board JAC Class 9 Maths Solutions Chapter 2 Polynomials Ex 2.5 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 2 Polynomials Ex 2.5

Question 1.
Use suitable identities to find the following products:
(i) (x + 4) (x + 10)
(ii) (x + 8) (x – 10)
(iii) (3x + 4) (3x – 5)
(iv) (y² + 3/2) (y² – 3/2)
(v) (3 – 2x) (3 + 2x)
Answer:
(i) Using identity, (x + a) (x + b)
= x² + (a + b) x + ab
In (x + 4) (x + 10), a = 4 and b = 10
Now,
(x + 4) (x + 10)
= x² + (4 + 10)x + (4 × 10)
= x² + 14x+ 40

(ii) (x + 8) (x – 10)
Using identity, (x + a) (x + b)
= x² + (a + b) x + ab
Here, a = 8 and b = -10
(x + 8) (x – 10)
= x² + {8 + (- 10)}x + {8 × (- 10)}
= x² + (8 – 10)x – 80
= x² – 2x – 80

(iii) (3x + 4) (3x – 5)
Using identity, (x + a) (x + b)
= x² + (a + b) x + ab
Here, x as 3x, a = 4 and b = – 5
(3x + 4) (3x – 5)
= (3x)² + {4 + (-5)}3x + {4 × (-5)}
= 9x² + 3x(4 – 5) – 20
= 9x² – 3x – 20

(iv) (y² + 3/2) (y² – 3/2)
Using identity, (x + y) (x – y) = x² – y²
Here, x = y² and y = 3/2
(y² + 3/2) (y² – 3/2)
= (y²)² – (3/2)²
= y⁴ – 9/4

(v) (3 – 2x) (3 + 2x)
Using identity, (x + y) (x – y) = x² – y²
Here, x = 3 and y = 2x
(3 – 2x) (3 + 2x)
= 3² – (2x)²
= 9 – 4x²

Question 2.
Evaluate the following products without multiplying directly:
(i) 103 × 107
(ii) 95 × 96
(iii) 104 × 96
Answer:
(i) 103 × 107
Answer:
(i) 103 × 107 = (100 + 3) (100 + 7)
Using identity, (x + a) (x + b)
= x² + (a + b) x + ab
Here, x = 100, a = 3 and b = 7
103 × 107 = (100 + 3) (100 + 7)
= (100)²+ (3 + 7)100 + (3 × 7)
= 10000 + 1000 + 21 = 11021

(ii) 95 × 96 = (90 + 5) (90 + 6)
Using identity, (x + a) (x + b)
= x² + (a + b) x + ab
Here, x = 90, a = 5 and b = 6
95 × 96 = (90 + 5) (90 + 6)
= 90² + 90(5 + 6) + (5 × 6)
= 8100 + (11 × 90) + 30 = 8100 + 990 + 30 = 9120

(iii) 104 × 96 = (100 + 4) (100 – 4)
Using identity, (x + y) (x – y) = x² – y²
Here, x = 100 and y = 4
104 × 96 = (100 + 4) (100 – 4)
= (100)² – (4)²
= 10000 – 16 = 9984

Question 3.
Factorise the following using appropriate identities:
(i) 9x² + 6xy + y²
(ii) 4y² – 4y + 1
(iii) x² – \(\frac{y^2}{100}\)
Answer:
(i) 9x² + 6xy + y²
= (3x)² + (2 × 3x × y) + y²
Using identity, (a + b)² = a² + 2ab + b²
Here, a = 3x and b = y
9x² + 6xy + y²
= (3x)² + (2 × 3x × y) + y²
= (3x + y)²
= (3x + y) (3x + y)

(ii) 4y² – 4y + 1
= (2y)² – (2 × 2y × 1) + 1²
Using identity, (a – b)² = a² – 2ab + b²
Here, a = 2y and b = 1
4y² – 4y + 1
= (2y)² – (2 × 2y × 1) + 1²
= (2y – 1)²
= (2y – 1) (2y – 1)

(iii) x² – \(\frac{y^2}{100}\) = x²– (\(\frac{y}{10}\))²
Using identity, a² – b²= (a + b) (a – b)
Here, a = x and b = (\(\frac{y}{10}\))
x² – \(\frac{y^2}{100}\) = x² – (\(\frac{y^2}{100}\))²
= (x – \(\frac{y}{10}\)) (x + \(\frac{y}{10}\))

Page – 49

Question 4.
Expand each of the following, using suitable identities:
(i) (x + 2y + 4z)²
(ii) (2x – y + z)²
(iii) (-2x + 3y + 2z)²
(iv) (3a – 7b – c)²
(v) (-2x + 5y – 3z)²
(vi) [\(\frac{1}{4}\) a – \(\frac{1}{2}\) b + 1]²
Answer:
(i) (x + 2y + 4z)²
Using identity, (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
Here, a = x, b = 2y and c = 4z
(x + 2y + 4z)²
= x² + (2y)² + (4z)² + (2 × x × 2y) + (2 × 2y × 4z) + (2 × 4z × x)
= x² + 4y² + 16z² + 4xy + 16yz + 8xz

(ii) (2x – y + z)²
Using identity, (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
Here, a = 2x, b = – y and c = z
(2x – y + z)²
= (2x)² + (-y)² + z² + (2 × 2x × (- y)) + (2 × (- y) × z) + (2 × z × 2x)
= 4x² + y² + z² – 4xy – 2yz + 4xz

(iii) (-2x + 3y + 2z)²
Using identity, (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
Here, a = – 2x, b = 3y and c = 2z
(-2x + 3y + 2z)²
=(-2x)² + (3y)² + (2z)² + (2 × (- 2x) × 3y) + (2 × 3y × 2z) + (2 × 2z × (- 2x))
= 4x² + 9y² + 4z² – 12xy + 12yz – 8xz

(iv) (3a – 7b – c)²
Using identity, (a + b + c)² = a² + b²+ c² + 2ab + 2bc + 2ca
Here, a = 3a, b = – 7b and c = – c
(3a – 7b – c)²
= (3a)² + (-7b)² + (-c)² + (2 × 3a × (-7b)) + (2 × (- 7b) × (- c)) + (2 × (- c) × 3a)
= 9a² + 49b² + c² – 42ab + 14bc – 6ac

(v) (-2x + 5y – 3z)²
Using identity, (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
Here, a = – 2x, b = 5y and c = – 3z
(-2x + 5y – 3z)²
= (-2x)² + (5y)² + (-3z)² + (2 × (-2x) × 5y) + (2 × 5y × (- 3z)) + (2 × (- 3z) × (- 2x))
= 4x² + 25y² + 9z² – 20xy – 30yz + 12xz

(vi) [\(\frac{1}{4}\) a – \(\frac{1}{2}\) b + 1]²
Using identity, (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
Here, a = \(\frac{1}{4}\)a; b = \(\frac{1}{2}\) and c = 1
[\(\frac{1}{4}\) a – \(\frac{1}{2}\) b + 1]²
= \(\left(\frac{1}{4} \mathrm{a}\right)^2+\left(-\frac{1}{2} \mathrm{~b}\right)^2+1^2+\left(2 \times \frac{1}{4} \mathrm{a} \times \frac{(-1)}{2} \mathrm{~b}\right)+\left(2 \times \frac{(-1)}{2} \mathrm{~b} \times 1\right)+\left(2 \times 1 \times \frac{1}{4} \mathrm{a}\right)\)
= \(\frac{1}{16} \mathrm{a}^2+\frac{1}{4} \mathrm{~b}^2+1-\frac{1}{4} \mathrm{ab}-\mathrm{b}+\frac{1}{2} \mathrm{a}\)

Question 5.
Factorise:
(i) 4x² + 9y² + 16z² + 12xy – 24yz – 16xz
(ii) 2x² + y² + 8z² – 2\( \sqrt{2} \)xy + 4 \( \sqrt{2} \) yz – 8xz
Answer:
(i) 4x² + 9y² + 16z² + 12xy – 24yz -16xz
Using identity, (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
4x² + 9y² + 16z² + 12xy – 24yz – 16xz
= (2x)² + (3y)² + (-4z)² + (2 × 2x × 3y) + (2 × 3y × (- 4z)) + (2 × (- 4z) × 2x)
= (2x + 3y – 4z)² = (2x + 3y – 4z) (2x + 3y – 4z)

(ii) 2x² + y² + 8z² – 2 \( \sqrt{2} \) xy + 4 \( \sqrt{2} \) yz – 8xz
Using identity, (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
2×2 + y2 + 8z2 – 2 \( \sqrt{2} \) xy + 4 \( \sqrt{2} \) yz – 8xz
= (-\( \sqrt{2} \) x)² + (y)² + (2\( \sqrt{2} \)z)² + (2 × (- \( \sqrt{2} \) x) × y) + (2 × y × 2 \( \sqrt{2} \) z) + (2 × 2\( \sqrt{2} \) z × (- \( \sqrt{2} \)x))
= (-V/2x + y+ 2>/2z)² = (-V2x + y + 2 \( \sqrt{2} \) z) (- \( \sqrt{2} \) x + y + 2 \( \sqrt{2} \) z)

Question 6.
Write the following cubes in expanded form:
(i) (2x + 1)³
(ii) (2a – 3b)³
(iii) \(\left[\frac{3}{2} x+1\right]^3\)
(iv) \(\left[x-\frac{2}{3} y\right]^3\)
Answer:
(i) (2x + 1)³
Using identity, (a + b)³ = a³ + b³ + 3ab(a + b)
(2x+1)³ = (2x)³ + 1³ + (3 × 2x × 1)(2x + 1) = 8x³ + 1 + 6x(2x + 1)
= 8x³ + 12x² + 6x + 1

(ii) (2a – 3b)³
Using identity, (a – b)³ = a³ – b³ – 3ab(a – b)
(2a – 3b)³
= (2a)³ – (3b)³ – (3 × 2a × 3b)(2a – 3b) = 8a³ – 27b³ – 18ab(2a – 3b)
= 8a³ – 27b³ – 36a²b + 54ab²

(iii) \(\left[\frac{3}{2} x+1\right]^3\)
Using identity, (a – b)³ = a³ – b³ – 3ab(a – b)

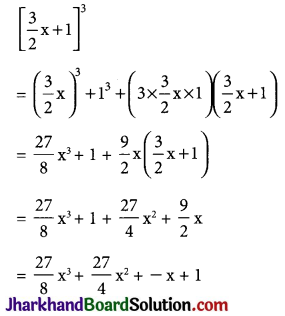
(iv) \(\left[x-\frac{2}{3} y\right]^3\)
Using identity, (a – b)³ = a³ – b³ – 3ab(a – b)

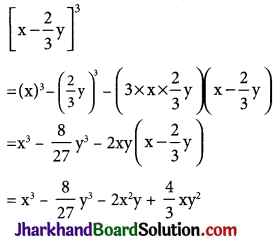
Question 7.
Evaluate the following using suitable identities:
(i) (99)³
(ii) (102)³
(iii) (998)³
Answer:
(i) (99)³ = (100 – 1)³
Using identity, (a – b)³ = a³ – b³ – 3ab(a – b)
(99)³ = (100 – 1)³
= (100)³ – (1)³ – (3 × 100 × 1) (100 – 1)
= 1000000 – 1 – 30000 + 300
= 970299

(ii) (102)³ = (100 + 2)³
Using identity, (a – b)³ = a³ – b³ – 3ab(a – b)
(100 + 2)³
= (100)³ + (2)³ + (3 × 100 × 2) (100 + 2)
= 1000000 + 8 + 600 (100 + 2)
= 1000000 + 8 + 60000 + 1200
= 1061208

(iii) (998)³ = (1000 – 2)³
Using identity, (a – b)³ = a³ – b³ – 3ab(a – b)
= (1000)³ – (2)³ – (3 × 1000 × 2) (1000 – 2)
= 1000000000 – 8 – 6000 × (1000 – 2)
= 1000000000 – 8 – 6000000 + 12000
= 1000012000 – 6000008
= 994011992

Question 8.
Factorise each of the following:
(i) 8a³ + b³ + 12a²b + 6ab²
(ii) 8a³ – b³ – 12a²b + 6ab²
(iii) 27 – 125a³ – 135a + 225a²
(iv) 64a³ – 27b³ – 144a²b + 108ab²
(v) 27p³ – \(\frac{1}{216}-\frac{9}{2}\)p² + \(\frac {1}{4}\)p
Answer:
(i) 8a³ + b³ + 12a²b + 6ab²
Using identity, (a + b)³ = a³ + b³ + 3a²b + 3ab²
= (2a)³ + (b)³ + 3 (2a) (b) (2a + b)
= (2a + b)³
= (2a + b) (2a + b) (2a + b)

(ii) 8a³ – b³ – 12a²b + 6ab²
Using identity, (a + b)³ = a³ + b³ + 3a²b + 3ab²
= (2a)³ – (b)³ – 3 (2a)(b)(2a – b)
= (2a – b)³ = (2a – b)(2a – b)(2a – b)

(iii) 27 – 125a³ – 135a + 225a²
Using identity, (a + b)³ = a³ + b³ + 3a²b + 3ab²
= (3)³ – (5a)³ – 3(3)(5a) (3 – 5a)
= (3 – 5a)³ = (3 – 5a) (3 – 5a) (3 – 5a)

(iv) 64a³ – 27b³ – 144a²b + 108aba²
Using identity, (a + b)³ = a³ + b³ + 3a²b + 3ab²
= (4a)³ – (3b)³ – 3 (4a) (3b) (4a – 3b)
= (4a – 3b)³
= (4a – 3b) (4a – 3b) (4a – 3b)

(v) 27p³ – \(\frac{1}{216}-\frac{9}{2}\)p² + \(\frac {1}{4}\)p
Using identity, (a + b)³ = a³ + b³ + 3a²b + 3ab²

Question 9.
Verify:
(i) x³ + y³ = (x + y) (x² – xy + y²)
(ii) x³ – y³ = (x – y) (x² + xy + y²)
Answer:
(i) (x + y) (x² – xy + y²)
We know that,
(x + y)³ = x³ + y³ + 3xy(x + y)
⇒ x³ + y³ = (x + y)³ – 3xy(x + y)
⇒ x³ + y³ = (x + y)[(x + y)² – 3xy] {Taking (x + y) common}
⇒ x³ + y³ = (x + y) (x² + y² – xy)
⇒ x³ + y³ = (x + y) (x² + xy + y²)

(ii) x³ – y³ = (x – y) (x² + xy + y²)
We know that,
(x – y)³ = x³ + y³ – 3xy(x – y)
⇒ x³ – y³ = (x – y)³ + 3xy(x – y)
⇒ x³ + y³ = (x – y)[(x – y)² + 3xy] {Taking (x – y) common}
⇒ x³ + y³ = (x – y) [(x² + y² – 2xy) + 3xy]
⇒ x³ + y³ = (x + y)(x² + y² + xy)

Question 10.
Factorise each of the following:
(i) 27y³ + 125z³
(ii) 64m³ – 343n³
Answer:
(i) 27y³ + 125z³
Using identity, x³ + y³ = (x + y)(x² + y² + xy)
= (3y + 5z) [(3y)² – 3y × 5z + (5z)²]
= (3y + 5z) [9y² – 15yz + 25z²]

(ii) 64m³ – 343n³
Using identity, x³ + y³ = (x + y)(x² + y² + xy)
= (4m – 7n) [(4m)² + 4m × 7n + (7n)²]
= (4m – 7n) [16m² + 28mn + 49n²]

Question 11.
Factorise: 27x³ + y³ + z³ – 9xyz
Answer:
27x³ + y³ + z³ – 9xyz
= (3x)³ + y³ + z³ – 3 × (3x) yz
Using identity, x³ + y³ + z³ – 3xyz
= (x + y + z)(x² + y² + z² – xy – yz – xz)
27x³ + y³ + z³ – 9xyz
= (3x + y + z) [(3x)² + (y)² + (z)² – 3xy – yz – 3xz]
= (3x + y + z) (9x² + y² + z² – 3xy – yz – 3xz)

Question 12.
Verify that: x³ + y³ + z³ – 3xyz = \(\frac {1}{2}\)(x + y + z) [(x – y)² + (y – z)² + (z – x)²]
Answer:
We know that,
x³ + y³ + z³ – 3xyz
= (x + y + z)(x² + y² + z² – xy – yz – xz)
⇒ x³ + y³ + z³ – 3xyz
= \(\frac {1}{2}\) × (x + y + z) 2(x² + y²+ z² – xy – yz – xz)
= \(\frac {1}{2}\)(x + y + z)(2x² + 2y² + 2z² – 2xy – 2yz – 2xz)
= \(\frac {1}{2}\)(x + y + z) [(x² + y² – 2xy) + (y² + z² – 2yz) + (x² + z² – 2xz)]
= \(\frac {1}{2}\)(x + y + z) [(x – y)²+ (y – z)² + (z – x)²]

Question 13.
If x + y + z = 0, show that x³ + y³ + z³ = 3xyz.
Answer:
We know that,
x³ + y³ + z³
= (x² + y²+ z² – xy – yz – xz)
Now put (x + y + z) = 0,
(x² + y²+ z² – xy – yz – xz) – 3xyz = (0)(x² + y²+ z² – xy – yz – xz)
⇒ x³ + y³ + z³ = 3xyz

Question 14.
Without actually calculating the cubes, find the value of each of the following:
(i) (-12)³ + (7)³ + (5)³
(ii) (28)³ + (-15)³ + (-13)³
Answer:
(i) (-12)³ + (7)³ + (5)³
Let x = – 12, y = 7 and z = 5
We observed that,
x + y + z = -12 + 7 + 5 = 0
We know that if, x + y + z = 0,
then x³ + y³ + z³ = 3xyz
(-12)³ + (7)³ + (5)³ = 3(-12)(7)(5)
= – 1260

(ii) (28)³ + (-15)³ + (-13)³
Let x = 28, y = – 15 and z = – 13
We observed that,
x + y + z = 28 – 15 – 13 = 0
We know that if, x + y + z = 0,
then x³ + y³ + z³ = 3xyz
(28)³ + (-15)³ + (-13)³
= 3(28)(-15)(-13) = 16380

Question 15.
Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given:
(i) Area: 25a² – 35a +12
(ii) Area: 35y² + 13y – 12
Answer:
(i) Area: 25a² – 35a +12
Since, area is product of length and breadth therefore by factorising the given area, we can know the length and breadth of rectangle.
25a² – 35a +12 = 25a² – 15a – 20a + 12
= 5a(5a – 3) – 4(5a – 3) = (5a – 4) (5a -3 )
Possible expression for length = 5a – 3
Possible expression for breadth = 5a – 4

(ii) Area: 35y² + 13y – 12
35y² + 13y – 12 = 35y² – 15y + 28y – 12
= 5y(7y – 3) + 4(7y – 3) = (5y + 4)(7y – 3)
Possible expression for length = (5y + 4)
Possible expression for breadth = (7y – 3)

Page – 50

Question 16.
What are the possible expressions for the dimensions of the cuboids whose volumes are given below?
(i) Volume: 3x² – 12x
(ii) Volume : 12ky² + 8ky – 20k
Answer:
(i) Volume: 3x² – 12x
Since, volume is product of length, breadth and height therefore by factorising the given volume, we can know the length, breadth and height of the cuboid.
3x² – 12x = 3x(x – 4)
Possible expression for length = 3
Possible expression for breadth = x
Possible expression for height = (x – 4)

(ii) Volume : 12ky² + 8ky – 20k
Since, volume is product of length, breadth and height therefore by factorising the given volume, we can know the length, breadth and height of the cuboid.
12ky² + 8ky – 20k = 4k(3y² + 2y – 5) = 4k(3y² +5y – 3y – 5)
= 4k[y(3y + 5) – 1(3y + 5)]
= 4k (3y + 5) (y – 1)
Possible expression for length = 4k
Possible expression for breadth = (3y + 5)
Possible expression for height = (y – 1)

JAC Jharkhand Board Class 12th Geography Important Questions in Hindi & English Medium

JAC Board Class 12th Geography Important Questions in Hindi Medium

Jharkhand Board Class 12th Geography Important Questions: मानव भूगोल के मूल सिद्धान्त

• Chapter 1 मानव भूगोल – प्रकृति एवं विषय क्षेत्र Important Questions
• Chapter 2 विश्व जनसंख्या वितरण, घनत्व और वृद्धि Important Questions
• Chapter 3 जनसंख्या संघटन Important Questions
• Chapter 4 मानव विकास Important Questions
• Chapter 5 प्राथमिक क्रियाएँ Important Questions
• Chapter 6 द्वितीयक क्रियाएँ Important Questions
• Chapter 7 तृतीयक और चतर्थ क्रियाकलाप Important Questions
• Chapter 8 परिवहन एवं संचार Important Questions
• Chapter 9 अंतर्राष्ट्रीय व्यापार Important Questions
• Chapter 10 मानव बस्ती Important Questions

Jharkhand Board Class 12th Geography Important Questions: भारत : लोग और अर्थव्यवस्था

• Chapter 1 जनसंख्या : वितरण, घनत्व, वृद्धि और संघटन Important Questions
• Chapter 2 प्रवास : प्रकार, कारण और परिणाम Important Questions
• Chapter 3 मानव विकास Important Questions
• Chapter 4 मानव बस्तियाँ Important Questions
• Chapter 5 भूसंसाधन तथा कृषि Important Questions
• Chapter 6 जल-संसाधन Important Questions
• Chapter 7 खनिज तथा ऊर्जा संसाधन Important Questions
• Chapter 8 निर्माण उद्योग Important Questions
• Chapter 9 भारत के संदर्भ में नियोजन और सततपोषणीय विकास Important Questions
• Chapter 10 परिवहन तथा संचार Important Questions
• Chapter 11 अंतर्राष्ट्रीय व्यापार Important Questions
• Chapter 12 भौगोलिक परिप्रेक्ष्य में चयनित कुछ मुद्दे एवं समस्याएँ Important Questions

JAC Board Class 12th Geography Important Questions in English Medium

JAC Board Class 12th Geography Important Questions: Fundamentals of Human Geography

• Chapter 1 Human Geography : Nature and Scope Important Questions
• Chapter 2 The World Population : Distribution, Density and Growth Important Questions
• Chapter 3 Population Composition Important Questions
• Chapter 4 Human Development Important Questions
• Chapter 5 Primary Activities Important Questions
• Chapter 6 Secondary Activities Important Questions
• Chapter 7 Tertiary and Quaternary Activities Important Questions
• Chapter 8 Transport and Communication Important Questions
• Chapter 9 International Trade Important Questions
• Chapter 10 Human Settlements Important Questions

JAC Board Class 12th Geography Important Questions: India : People and Economy

• Chapter 1 Population : Distribution, Density, Growth and Composition Important Questions
• Chapter 2 Migration : Types, Causes and Consequences Important Questions
• Chapter 3 Human Development Important Questions
• Chapter 4 Human Settlements Important Questions
• Chapter 5 Land Resources and Agriculture Important Questions
• Chapter 6 Water Resources Important Questions
• Chapter 7 Mineral and Energy Resources Important Questions
• Chapter 8 Manufacturing Industries Important Questions
• Chapter 9 Planning and Sustainable Development in Indian Context Important Questions
• Chapter 10 Transport and Communication Important Questions
• Chapter 11 International Trade Important Questions
• Chapter 12 Geographical Perspective on Selected Issues and Problems Important Questions