JAC Class 9 Maths Important Questions Chapter 4 Linear Equations in Two Variables

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 4 Linear Equations in Two Variables Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 4 Linear Equations in Two Variables

Question 1.
Prove that x = 3, y = 2 is a solution of 3x – 2y = 5.
Solution :
x = 3, y = 2 is a solution of 3x – 2y = 5, because L.H.S. = 3x – 2y = 3 × 3 – 2 × 2 = 9 – 4 = 5 = R.H.S.
i.e. x = 3, y = 2 satisfies the equation 3x – 2y = 5.
∴ It is a solution of the given equation.

Question 2.
Prove that x = 1, y = 1 as well as x = 2, y = 5 is a solution of 4x – y – 3 = 0.
Solution :
Given eq, is 4x – y – 3 = 0 …(i)
First we put x = 1, y = 1 in L.H.S. of eq (i)
Here L.H.S. = 4x – y – 3 = 4 × 1 – 1 – 3 = 4 – 4 = 0 = R.H.S.
Now we put x = 2, y = 5 in eq. (i)
L.H.S. = 4x – y – 3 = 4 × 2 – 5 – 3 = 8 – 8 = 0 = R.H.S.
Since, x = 1, y = 1 and x = 2, y = 5, both pairs satisfied the given equation, therefore they are the solutions of given equation.

Question 3.
Determine whether x = 2, y = – 1 is a solution of equation 3x + 5y – 2 = 0.
Solution :
Given eq. is 3x + 5y – 2 = 0 ….(i)
Taking L.H.S. = 3x + 5y – 2 = 3 × 2 + 5 × (-1) – 2 = 6 – 5 – 2 = – 1 + 0 = R.H.S.
Here LH.S. ≠ R.H.S. therefore x = 2, y = – 1 is not a solution of given equation.

Question 4.
Draw the graph of
(i) 2x + 5 = 0
(ii) 3y – 15 = 0

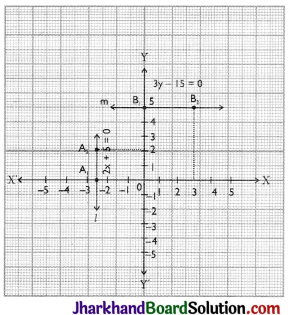
Solution :
(i) Graph of 2x + 5 = 0
On simplifying it we get 2x = – 5
x = – \(\frac {5}{2}\)
First we plot point A₁ (-\(\frac {5}{2}\), 0) and then we plot any other point A₂ (-\(\frac {5}{2}\), 2) on the graph paper, then we join these two points we get required line l as shown in adjoining figure

(ii) Graph of 3y – 15 = 0
On simplifying it we get 3y = 15 y = 5.
⇒ y = \(\frac {15}{3}\) = 5
First we plot the point B₁(0, 5) and then we plot any other point B₂(3, 5) on the graph paper, then we join these two points we get required line m as shown in figure.
Note: A point which lies on the line is a solution of that equation. A point not lying on the line is not a solution of the equation.

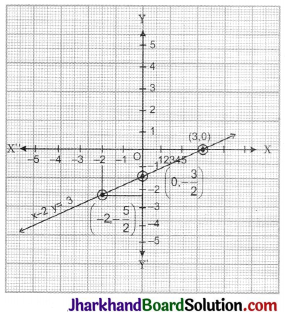
Question 5.
Draw the graph of the line x – 2y = 3, from the graph find the coordinates of the point when
(i) x = – 5
(ii) y = 0

Solution :
Here given equation is x – 2y = 3.
Solving it for y we get 2y = x – 3
⇒ y = \(\frac {1}{2}\)x – \(\frac {3}{2}\)
Let x = 0, then y = \(\frac {1}{2}\)(0) – \(\frac {3}{2}\) = – \(\frac {3}{2}\)
x = 3, then y = \(\frac {1}{2}\)(3) – \(\frac {3}{2}\) = 0
x = – 2, then y Hence, we get y = \(\frac {1}{2}\)(-2) – \(\frac {3}{2}\) = – \(\frac {5}{2}\)
Hence, we get

x	0	3	– 2
Y	–\(\frac {3}{2}\)	0	–\(\frac {5}{2}\)

Clearly from the graph, when x = -5 then y = -4 so corresponding coordinates are (-5, -4) and when y = 0 then x = 3, so corresponding coordinates are (3, 0).

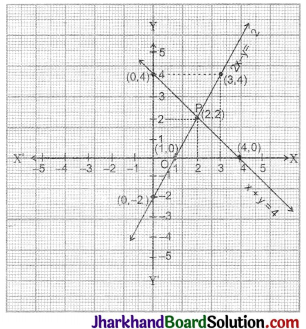
Question 6.
Draw the graphs of the lines represented by the equations x + y = 4 and 2x – y = 2 in the same graph. Also find the coordinates of the point where the two lines intersect.

Solution :
Given equations are x + y = 4 ………….(i)
and 2x – y = 2 ….. (ii)
(i) We have, y = 4 – x

x	0	2	4
Y	4	2	0

(ii) We have, y = 2x – 2

x	1	0	3
Y	0	– 2	4

By drawing the lines on a graph paper, clearly we can say that P is the point of intersection where coordinates are x = 2, y = 2, i.e., P(2, 2).

Question 7.
Solve : \(\frac {x}{2}\) = 3 + \(\frac {x}{3}\)
Solution :
Given \(\frac {x}{2}\) = 3 + \(\frac {x}{3}\)
⇒ \(\frac {x}{2}\) – \(\frac {x}{3}\) = 3
⇒ \(\frac{3 x-2 x}{6}\) = 3
⇒ \(\frac {x}{6}\) = 3
⇒ x = 18

Question 8.
Solve the following system of equations:
2x – 3y = 5
3x + 2y = 1
Solution :
Given eq. are 2x – 3y = 5 ………(i)
and 3x + 2y = 1 ……………(ii)
Multiplying eq. (i) by 3 and eq. (ii) by 2. we get 6x – 9y = 15 and 6x + 4y = 2 respectively.

⇒ -13y = 13
⇒ y = – 1
Putting the value of y in eq. (i) we get
2x – (3) × (-1) = 5
2x + 3 = 5
⇒ 2x = 5 – 3
⇒ 2x = 2
⇒ x = 1
∴ x = 1, y = – 1 is the solution of given system of linear equations.

Question 9.
Solve the following system of equations:
x + 4y = 14
7x – 3y = 5
Solution :
Let x + 4y = 14 ……..(i)
and 7x – 3y = 5 ……….(ii)
From equation (i)
x = 14 – 4y
Substitute the value of x in equation (ii)
⇒ 7(14 – 4y) – 3y = 5
⇒ 98 – 28y – 3y = 5
⇒ 98 – 31y = 5
⇒ 93 = 3ly
⇒ y = \(\frac {93}{31}\)
⇒ y = 3
x = 14 – 4y = 14 – 4 × 3 = 14 – 12 = 2
So, solution is x = 2 and y = 3.

Multiple Choice Questions

Question 1.
Which of the following equations is not a linear equation?
(a) 2x + 3 = 7x – 2
(b) \(\frac {2}{3}\)x + 5 = 3x – 4
(c) x² + 3 = 5x – 3
(d) (x – 2)² = x² + 8
Solution :
(c) x² + 3 = 5x – 3

Question 2.
Solution of equation \(\sqrt{3}\)x – 2 = 2\(\sqrt{3}\) + 4 is
(a) 2(\(\sqrt{3}\) – 1)
(b) 2(1 – \(\sqrt{3}\))
(c) 1 + \(\sqrt{3}\)
(d) 2(1 + \(\sqrt{3}\))
Solution :
(d) 2(1 + \(\sqrt{3}\))

Question 3.
The value of x which satisfies \(\frac{6 x+5}{4 x+7}=\frac{3 x+5}{2 x+6}\) is :
(a) -1
(b) 1
(c) 2
(d) -2
Solution :
(b) 1

Question 4.
Solution of \(\frac{x-a}{b+c}+\frac{x-b}{c+a}+\frac{x-c}{a+b}\) = 3 is
(a) a + b – c
(b) a – b + c
(c) – a + b + c
(d) a + b + c
Solution :
(d) a + b + c

Question 5.
One-fourth of one-third of one-half of a number is 12, then number is
(a) 284
(b) 286
(c) 288
(d) 290
Solution :
(c) 288

Question 6.
A linear equation in two variables has maximum
(a) one solution
(b) two solutions
(c) infinitely many solutions
(d) None of these
Solution :
(c) infinitely many solutions

Question 7.
Solutions of the equation x – 2y = 2 is/are
(a) x = 4, y = 1
(b) x = 2, y = 0
(c) x = 6, y = 2
(d) All of these
Solution :
(d) All of these

Question 8.
The graph of line 5x + 3y = 4 cuts y-axis at the point
(a) (0, \(\frac {4}{3}\))
(b) (0, \(\frac {3}{4}\))
(c) (\(\frac {4}{3}\), 0)
(d) (\(\frac {4}{3}\), 0)
Solution :
(a) (0, \(\frac {4}{3}\))

Question 9.
If x = 1, y = 1 is a solution of equation 9ax + 12ay = 63, then the value of a is
(a) – 3
(b) 3
(c) 7
(d) 5
Solution :
(b) 3