Students should go through these JAC Class 9 Maths Notes Chapter 8 Quadrilaterals will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 8 Quadrilaterals
Quadrilateral
A quadrilateral is a closed figure obtained by joining four points (with no three points collinear) in an order.
→ Since, ‘quad’ means ‘four’ and ‘lateral’ is for ‘sides therefore quadrilateral means a figure bounded by four sides’
→ Every quadrilateral has:
(A) Four vertices
(B) Four sides
(C) Four angles and
(D) Two diagonals.
→ A diagonal is a line segment obtained on joining the opposite vertices.
Sum of the Angles of a Quadrilateral:
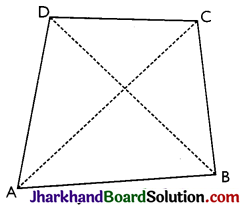
Consider a quadrilateral ABCD as shown in figure. Join A and C to get the diagonal AC which divides the quadrilateral ABCD into two triangles ABC and ADC.
We know the sum of the angles of each triangle is 180°
∴ In ΔABC; ∠CAB + ∠B + ∠BCA = 180°
and In ΔADC; ∠DAC + ∠D + ∠DCA = 180°
On adding, we get:
(∠CAB + ∠DAC) + ∠B + ∠D + (∠BCA + ∠DCA) = 180° + 180°
⇒ ∠A + ∠B + ∠D + ∠C = 360°
Thus, the sum of the angles of a quadrilateral is 360°.
![]()
Types of Quadrilaterals:
→ Trapezium: It is a quadrilateral in which one pair of opposite sides are parallel and one pair is unparallel. In the quadrilateral ABCD, drawn alongside, sides AB and DC are parallel and AD and BC are unparallel therefore it is a trapezium
→ Parallelogram: It is a quadrilateral in which both the pairs of opposite sides are equal and parallel. The figure shows a quadrilateral ABCD in which AB is parallel and equal to DC and AD is parallel and equal to BC, therefore ABCD is a parallelogram.
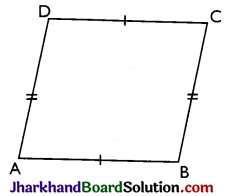
Here, (A) ∠A = ∠C and ∠B = ∠D
(B) AB = CD and AD = BC
(C) AB || CD and AD || BC
→ Rectangle: It is a parallelogram whose each angle is 90°.
(a) ∠A + ∠B = 90° + 90° = 180°
⇒ AD || BC, also AD = BC.
(b) ∠B + ∠C = 90° + 90° = 180°
⇒ AB || DC, also AB = DC.
(c) Diagonals AC and BD are equal.
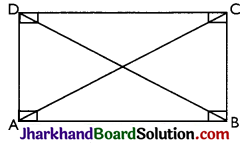
Rectangle ABCD is also a parallelogram.
→ Rhombus: It is a also parallelogram whose all the sides are equal and diagonals are perpendicular to each other. The figure shows a parallelogram ABCD in which AB = BC = CD = DA; AC ⊥ BD.; therefore it is a rhombus.
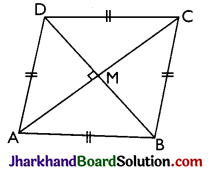
→ Square: It is a parallelogram whose all the sides are equal and each angle is 90°. Also, diagonals are equal and perpendicular to each other. The figure shows a parallelogram ABCD in which AB = BC = CD = DA, ∠A = ∠B = ∠C = ∠D = 90°, AC ⊥ BD and AC = BD, therefore ABCD is a square.
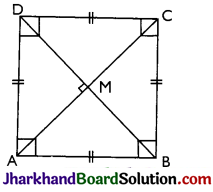
→ Kite: It is not parallelogram in which two pairs of adjacent sides are equal The figure shows a quadrilateral ABCD in which adjacent sides AB and AD are equal i.e. AB = AD and also the other pair of adjacent sides are equal i.e., BC = CD; therefore it is a kite or kite shaped figure.
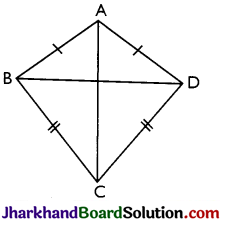
Remarks:
- Square, rectangle and rhombus are all parallelograms.
- Kite and trapezium are not parallelograms.
- A square is a rectangle.
- A square is a rhombus.
- A parallelogram is a trapezium.
![]()
Parallelogram Theorems
A parallelogram is a quadrilateral in which both the pairs of opposite sides are equal and parallel.
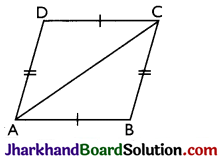
Theorem 1.
A diagonal of a parallelogram divides the parallelogram into two congruent triangles.
Proof:
Given: A parallelogram ABCD.
To Prove: A diagonal divides the parallelogram
into two congruent triangles i.e., if diagonal AC is drawn then ΔABC ≅ ΔCDA and if diagonal BD is drawn
then ΔABD ≅ ΔCDB.
Construction: Join A and C
Proof: Since, ABCD is a parallelogram
AB || DC and AD || BC
In ΔABC and ΔCDA
∠BAC = ∠DCA [Alternate angles]
∠BCA = ∠DAC [Alternate angles]
And, AC = AC [Common side]
∴ ΔABC ≅ ΔCDA [By ASA]
Similarly, we can prove that
ΔABD ≅ ΔCDB
Theorem 2.
In a parallelogram, opposite sides are equal.
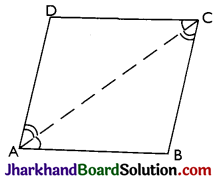
Proof:
Given: A parallelogram ABCD in which
AB || DC and AD || BC.
To Prove: Opposite sides are equal i.e.. AB = DC and AD = BC
Construction: Join A and C
Proof: In ΔABC and ΔCDA
∠BAC = ∠DCA [Alternate angles]
∠BCA = ∠DAC [Alternate angles]
AC = AC [Common]
∴ ΔABC ≅ ΔCDA [By ASA]
⇒ AB = DC and AD = BC [By CPCT]
Hence, proved.
Theorem 3.
If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
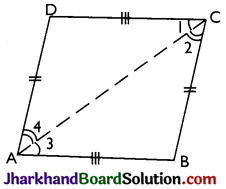
Proof:
Given: A quadrilateral ABCD in which AB = DC and AD = BC.
To Prove: ABCD is a parallelogram ie, AB || DC and AD || BC
Construction: Join A and C
Proof: In ΔABC and ΔCDA
AB = DC [Given]
AD = BC [Given]
And AC = AC [Common]
∴ ΔABC ≅ ΔCDA [By SSS]
⇒ ∠1 = ∠3 [By CPCT]
And ∠2 = ∠4 [By CPCT]
But these are alternate angles and whenever alternate angles are equal, the lines are parallel.
∴ AB || DC and AD || BC
⇒ ABCD is a parallelogram.
Hence, proved.
![]()
Theorem 4.
In a parallelogram, opposite angles are equal.
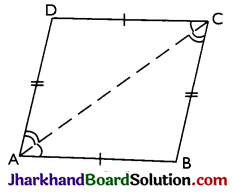
Proof:
Given: A parallelogram ABCD in which AB || DC and AD || BC.
To Prove: Opposite angles are equal i.e. ∠A = ∠C and ∠B = ∠D
Construction: Draw diagonal AC.
Proof: In ΔABC and ΔCDA
∠BAC = ∠DCA [Alternate angles]
∠BCA = ∠DAC [Alternate angles]
AC = AC [Common]
∴ ΔABC ≅ ΔCDA [By ASA]
⇒ ∠B = ∠D [By CPCT]
Similarly, we can prove that
∠A = ∠C Hence, proved.
Theorem 5.
If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
Proof:
Given: A quadrilateral ABCD in which opposite angles are equal. i.e., ∠A = ∠C and ∠B = ∠D
To prove: ABCD is a parallelogram i.e.,
AB || DC and AD || BC
Proof: Since the sum of the angles of quadrilateral is 360°
⇒ ∠A + ∠B + ∠C+ ∠D = 360°
⇒ ∠A + ∠D + ∠A + ∠D = 360°
[∵ ∠A = ∠C and ∠B = ∠D]
⇒ 2∠A + 2∠D = 360°
⇒ ∠A + ∠D = 180°
[∵ The sum of interior angles on the same side of transversal AB is 180°]
⇒ AB || DC
Similarly, ∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠A + ∠B + ∠A + ∠B = 360°
[∵ ∠A = ∠C and ∠B = ∠D]
⇒ 2∠A + 2∠B = 360°
⇒ ∠A + ∠B = 180°
[∵ The sum of interior angles on the same side of transversal AB is 180°]
∴ AD || BC
So, AB || DC and AD || BC
⇒ ABCD is a parallelogram.
Hence, proved.
Theorem 6.
The diagonal of a parallelogram bisect each other.
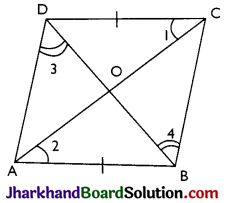
Proof:
Given: A parallelogram ABCD. Its diagonals AC and BD intersect each other at point O..
To Prove: Diagonals AC and BD bisect each other i.e., OA = OC and OB = OD.
Proof: In ΔAOB and ΔCOD
∵ AB || DC and BD is a transversal.
∴ ∠ABO = ∠CDO [Alternate angles]
∵ AB || DC and AC is a transversal line.
∴ ∠BAO = ∠DCO [Alternate angles]
And, AB = DC
⇒ ΔAOB ≅ ΔCOD [By ASA]
⇒ OA = OC and OB = OD [By CPCT]
Hence, proved.
![]()
Theorem 7.
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
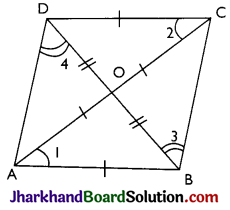
Proof:
Given: A quadrilateral ABCD whose diagonals AC and BD bisect each other at point O.
i.e., OA = OC and OB = OD
To prove: ABCD is a parallelogram i.e..
AB || DC and AD || BC.
Proof: In ΔAOB and ΔCOD
OA = OC [Given]
OB = OD [Given]
And, ∠AOB = ∠COD [Vertically opposite angles]
⇒ ΔAOB ≅ ΔCOD [By SAS]
⇒ ∠1 = ∠2 [By CPCT]
But these are alternate angles and whenever alternate angles are equal, the lines are parallel.
∴ AB is parallel to DC ie., AB || DC Similarly,
ΔAOD ≅ ΔCOB [By SAS]
⇒ ∠3 = ∠4
But these are also alternate angles
⇒ AD || BC
AB || DC and AD || BC
⇒ ABCD is parallelogram.
Hence, proved.
Theorem 8.
A quadrilateral is a parallelogram, if a pair of opposite sides is equal and parallel.
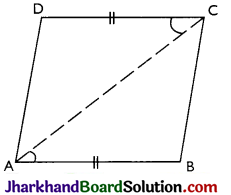
Proof:
Given: A quadrilateral ABCD in which AB = DC and AB || DC.
To Prove: ABCD is a parallelogram, i.e. AB || DC and AD || BC.
Construction: Join A and C.
Proof: Since AB is parallel to DC and AC is transversal
∠BAC = ∠DCA [Alternate angles]
AB = DC [Given]
And AC = AC [Common]
⇒ ΔBAC ≅ ΔDCA [By SAS]
⇒ ∠BCA = ∠DAC [By CPCT]
But these are alternate angles and whenever alternate angles are equal, the lines are parallel.
⇒ AD || BC
Now, AB || DC (given) and AD || BC
[Proved above]
⇒ ABCD is a parallelogram
Hence, proved.
Remarks:
In order to prove that given quadrilateral is parallelogram, we can prove any one of the following.
- Opposite angles of the quadrilateral are equal, or
- Diagonals of the quadrilateral bisect each other, or
- A pair of opposite sides is parallel and is of equal length, or
- Opposite sides are equal.
- Every diagonal divides the parallelogram into two congruent triangles.
![]()
Mid-Point Theorem
Statement: In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side and is half of it.
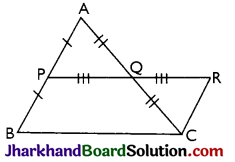
Given: A triangle ABC in which P is the mid-point of side AB and Q is the mid-point of side AC.
To Prove: PQ is parallel to BC and is half of it
i.e., PQ || BC and PQ = \(\frac{1}{2}\)BC
Construction: Produce PQ upto point such that PQ = QR. Join R and C.
Proof: In ΔAPQ and ΔCRQ
PQ = QR [By construction]
AQ = QC [Given]
And, ∠AQP = ∠CQR [Vertically opposite angles]
⇒ ΔAPQ ≅ ΔCRQ [By SAS]
⇒ AP = CR [By CPCT]
And, ∠APQ = ∠CRQ [By CPCT]
But, ∠APQ and ∠CRQ are alternate angles and we know, whenever the alternate angles are equal, the lines are parallel.
⇒ AP || CR
⇒ AB || CR
⇒ BP || CR
Given, P is mid-point of AB
⇒ AP = BP
⇒ CR = BP [As, AP = CR]
Now, BP = CR and BP || CR
⇒ BCRP is a parallelogram.
[When any pair of opposite sides are equal and parallel, the quadrilateral is a parallelogram]
BCRP is a parallelogram and opposite sides of a parallelogram are equal and parallel.
∴ PR = BC and PR || BC
Since, PQ = QR
⇒ PQ = \(\frac{1}{2}\)PR = \(\frac{1}{2}\)BC [AS, PR = BC]
Also, PQ || BC [As, PR || BC]
∴ PQ || BC and PQ = \(\frac{1}{2}\)BC
Hence, proved.
Converse of the Mid-Point Theorem
Statement: The line drawn through the midpoint of one side of a triangle parallel to the another side bisects the third side.
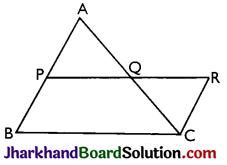
Given: A triangle ABC in which is the midpoint of side AB and PQ is parallel to BC.
To prove: PQ bisects the third side AC i.e., AQ = QC.
Construction: Through C, draw CR parallel to BA, which meets PQ produced at point R.
Proof: Since, PQ || BC i.e., PR || BC [Given]
CR || BA i.e., CR || BP [By construction]
∴ Opposite sides of quadrilateral PBCR are parallel.
⇒ PBCR is a parallelogram
⇒ BP = CR
Also, BP = AP [As Pis mid-point of AB]
∴ CR = AP (As CR = BP)
Now, AB || CR and AC is transversal, ∠PAQ = ∠ROQ [Alternate angles]
Also, AB || CR and PR is transversal, ∠APQ = ∠CRQ [Alternate angles]
In ΔAPQ and ΔCRQ
CR = AP, ∠PAQ = ∠RCQ and ∠APQ = ∠CRQ
⇒ ΔAPQ ≅ ΔCRO [By ASA]
⇒ AQ = QC Hence, proved.