JAC Board Class 9th Science Chapter 8 Notes Motion
→ An object is said to be in motion if it changes its position with the passage of time with respect to a fixed point in the background.
→ Types of Motion
a. Linear motion: A body is in linear motion if it moves in a straight line or path.
b. Circular motion (rotational): A body is in circular motion if it moves around a fixed point. A vertical line passing through the fixed point around which the body moves is known as axis of rotation.
c. Vibratory motion: A body has vibratory motion if it moves to and fro about a fixed point.
→ Concept of a Point object, Rest and Motion a. Point object: An extended object can be treated as a point object when the distance travelled by the object is much greater than its own size.
“A point object is one, which has no linear dimensions but possesses mass”.
b. Rest: A body is said to be at rest when its position does not change with time with respect to the observer.
c. Motion: A body is said to be in motion when its position changes with time with respect to the observer.
![]()
→ Vector and Scalar Quantities
a. Vector Quantities: The physical quantities that have magnitude as well as direction are called vector quantities.
Examples: Velocity, acceleration, force, displacement, momentum, weight, electric field, etc.
b. Scalar Quantities: The quantities that have only magnitude and no direction are called scalar quantities.
Examples: Mass, time, distance, speed, work, power, energy, charge, area, volume, density, pressure, potential, temperature, etc.
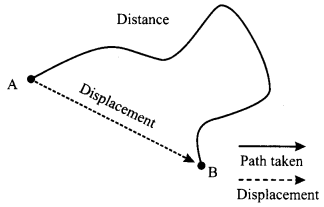
→ Distance and Displacement
a. Distance: It is the actual path travelled by an object from its initial position to its final position.
b. Displacement: It is the shortest straight line path between initial and final positions.
– If the initial and final points are same, displacement will be zero.
– Distance depends on path but displacement does not.
– Distance is always greater than or equal to displacement. They are equal only in straight line motion in a definite direction.
→ Uniform and Non-uniform Motion
a. Uniform motion is a motion in which equal distances are covered in equal time intervals.
b. Non-uniform motion is a motion in which unequal distances are covered in equal intervals of time.
→ Speed and Velocity
a. Speed: Speed is the distance travelled by an object in unit time.
Speed = \(\frac{\text { Distance travelled }}{\text { Time taken }}\)
or v = \(\frac{\mathrm{s}}{\mathrm{t}}\)
[where v = speed; s = distance; and t = time taken]
The SI unit of speed is m/s.
![]()
→ Average speed: It is the total distance travelled by the body divided by the total time taken to cover this distance.
Average speed = \(\frac{\text { Total distance travelled }}{\text { Total time taken }}\)
→ Uniform speed: When an object covers equal distances in equal intervals of time, however small these intervals may be, it is said to be in ‘uniform speed’.
→ Non-uniform speed: When an object covers unequal distances in equal intervals of time, it is said to be in ‘non-uniform speed’.
b. Velocity: It is the displacement of the body per unit of time. It is the distance travelled by a body per unit time in a given direction.
Velocity = \(\frac{\text { Displacement }}{\text { Time }}\)
The SI unit of velocity is m/s.
→ Important note: Velocity has both magnitude and direction while speed has only magnitude and no direction. Velocity has same direction as that of displacement.
→ Average velocity: The ratio of total displacement to the total time taken by the body gives its average velocity.
Average velocity = \(\frac{\text { Total displacement }}{\text { Total time taken }}\)
- Average speed is always greater than average velocity, except in case of straight line motion without U – turn, when both are equal.
- If body returns to its initial position, average velocity will be zero but average speed-will not be zero.
- When direction of motion changes, velocity also changes.
→ Instantaneous Speed and Velocity
a. Instantaneous speed: It is the speed of an object at a particular moment (instant) in time.
b. Instantaneous velocity: It is the velocity of an object in motion at a specific point in time.
→ Acceleration: Acceleration is the measure of change of velocity with time. It is also called rate of change of velocity. The SI unit of acceleration is m/s2. It is a vector quantity.
Acceleration = \(\frac{\text { Final velocity – Initial velocity }}{\text { Total time taken }}\)
If the velocity of an object changes from an initial value ‘u’ to the final value ‘v’ in time ‘f, the motion is called accelerated motion. In this case, acceleration ‘a’ is given by
a = \(\frac{\mathrm{v}-\mathrm{u}}{\mathrm{t}}\)
Accelerated motion is a motion in which acceleration is not equal to zero.
a. Acceleration has same direction as that of velocity, if velocity increases.
b. Acceleration has opposite direction as that of velocity, if velocity decreases. In this case, acceleration will be negative. Negative acceleration is also called retardation or deceleration.
![]()
→ Uniform and Non-uniform Acceleration
a. When velocity of a body changes by equal amounts in equal time intervals, acceleration is said to be uniform.
b. When velocity of body changes by unequal amounts in equal intervals of time, acceleration is said to be non-uniform.
Examples: A freely falling ball is under uniformly accelerated motion. A car driving by applying brakes frequently, is under non-uniformly accelerated motion.
→ Equations of Uniformly Accelerated Motion:
Relation among velocity, distance, time and acceleration gives the equation of motion. There are three equations of motion for bodies moving with uniform acceleration.
a. First Equation of Motion: v = u + at
b. Second Equation of Motion:
s = ut + \(\frac{1}{2}\) at2
c. Third Equation of Motion:
v2 = u2 + 2as
Here,
v = final velocity of the body
u = initial velocity of the body
a = acceleration of the body
t = time taken by the body
s = distance travelled by the body in time ‘t’
→ Average velocity in Uniformly Accelerated Motion: If a body moves a distance ‘s’ in time ‘t’
Average velocity = \(\frac{\text { Displacement }}{\text { Time }}=\frac{\mathrm{s}}{\mathrm{t}}\)
= u + \(\frac{1}{2}\)at (∵ s = ut + \(\frac{1}{2}\)at2)
or, u + \(\frac{1}{2}\)at = u + \(\frac{1}{2}\)(u – v) (∵ v = u + at)
= u + \(\frac{\mathrm{v}}{2}-\frac{\mathrm{u}}{2}=\frac{\mathrm{u}+\mathrm{v}}{2}\)
Here, ‘a’ is uniform acceleration of body.
Average velocity = \(\frac{u+v}{2}\)
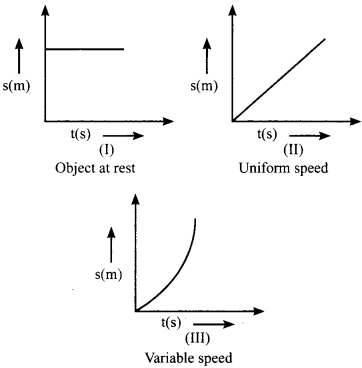
→ Graphical Representation of Motion: To describe the motion of an object, we can use different graphs. Graphical representation of motion shows dependence of one physical quantity, such as distance or velocity, on another quantity such as time.
a. Distance-time Graph: The change in the position of an object with time can be represented on the distance-time graph. The s-t graph for a moving body can be used to calculate the speed of the body.
b. Velocity-time Graph
– If a body moves with a uniform velocity (no acceleration), its speed-time graph would be a straight line parallel to time axis.
If a body moves with a non-uniform velocity (uniform acceleration), its speed time graph would be a straight line. If velocity increases (positive uniform acceleration) with time, graph would be a straight upward slope. If velocity decreases (negative uniform acceleration) with time, graph would be a straight downward slope.
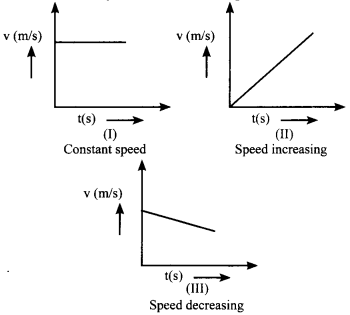
We can find out the magnitude of displacement (distance) and acceleration of a body using the velocity-time graph. The distance travelled by a moving body in a given time will be equal to the area under the speed-time graph.
![]()
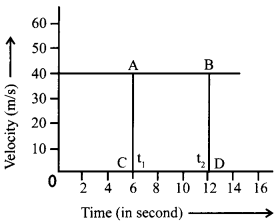
→ Velocity-time graph of an object moving with constant velocity
For the above graph,
Distance travelled = area of rectangle ABCD = AB × BD
s = v(t2 – t1)
Acceleration of body = \(\frac{\text { Change in velocity }}{\text { Time taken }}\)
As in above graph, velocity is constant, so in this case, acceleration will be zero.
→ Derivation of equation of motion using graphs:
Let an object move from A to B in time interval ‘f.
Acceleration of moving object = \(\frac{v_{2}-v_{1}}{t_{2}-t_{1}}\)
a. If initial velocity is u and final velocity is v then
a = \(\frac{v-u}{t-0}\)
at = v – u
v = u + at …(1)
Hence proved
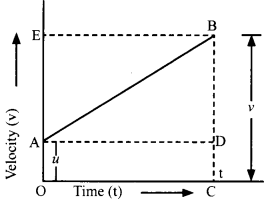
b. Distance travelled by object = area under graph
= area of rec. ADCO + area of triangle ABD
= (AO) (OC) + \(\frac{1}{2}\) (AD) (DB)
= ut + \(\frac{1}{2}\) (OC) (BC – CD)
= ut + \(\frac{1}{2}\) t (v – u)
= ut + \(\frac{1}{2}\) t (at)
or
s = ut + \(\frac{1}{2}\)at2 ….(2)
c. Distance travelled by object = area under graph
= area of trapezium AOCB
s = \(\frac{1}{2}\) (sum of ∥ sides) × t
S = \(\frac{1}{2}\) (u + v) × t …(i)
From first equation of motion, (v-u)
t = \(\frac{(v-u)}{a}\)
Equating equations (i) and (ii)
s = \(\frac{(v+u)(v-u)}{2 a}\) ……..(iii)
Hence proved
![]()
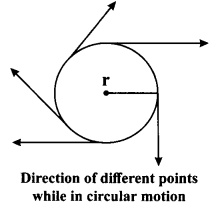
→ Circular Motion
a. Uniform circular motion is the motion in which an object moves on a circular path with constant speed. For example: moon revolving around the earth.
b. Non-uniform circular motion is the motion in which an object moves on circular path with varying speed. When an object is in circular motion, direction of its velocity keeps on changing.
→ Speed in the case of circular motion
Suppose a body is moving in a circular path of radius r.
Speed (v) = \(\frac{\text { Distance }}{\text { Time }}\)
= \(\frac{\text { Circumference of circle }}{\text { Time }}\)
= \(\frac{2 \pi r}{t}\)