JAC Board Class 9th Science Solutions Chapter 10 Gravitation
JAC Class 9th Science Gravitation InText Questions and Answers
Page 134
Question 1.
State the universal law of gravitation.
Answer:
The universal law of gravitation states that every object in the universe attracts every other object with a force called the gravitational force. The force acting between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres. For two objects of masses m1 and m2 separated by a distance r, the force (F) of attraction acting between them is given by the universal law of gravitation as:
F = \(=\frac{\mathrm{Gm}_{1} \mathrm{~m}_{2}}{\mathrm{R}^{2}}\)
where, G is the universal gravitational constant given by:
G = 6.67 × 10-2 Nm-2 kg-2.
![]()
Question 2.
Write the formula to find the magnitude of the gravitational force between the earth and an object on the surface of the earth.
Answer:
Let ME be the mass of the earth and m be the mass of an object on its surface.
If R is the radius of the earth, then according to the universal law of gravitation, the gravitational force (F) acting between the earth and the object is given by the relation:
F = \(=\frac{G M_{e} m}{R^{2}}\)
Page 136
Question 1.
What do you mean by free fall?
Answer:
Gravity of earth attracts every object towards its centre. When an object is dropped from a certain height, it begins to fall towards earth’s surface under the influence of gravitational force. Such a motion of object is called free fall.
Question 2.
What do you mean by acceleration due to gravity?
Answer:
When an object falls freely towards the surface of the earth from a certain height, its velocity changes. This change in velocity produces acceleration in the object which is known as acceleration due to gravity, denoted by ‘g’. The value of acceleration due to gravity is 9.8 m/s2.
Page 138
Question 1.
What are the differences between the mass of an object and its weight?
Answer:
| Mass | Weight |
| 1. Mass is the quantity of matter contained in a body. | 1. Weight is the force of gravity acting on a body. |
| 2. It is the measure of inertia of the body. | 2. It is the measure of gravity. |
| 3. Mass is a constant quantity. | 3. Weight is not a constant quantity. It is different at different places. |
| 4. It only has magnitude. | 4. It has magnitude as well as direction. |
| 5. Its SI unit is kilogram (kg) | 5. Its SI unit is the same as the SI unit of force, i.e., newton (N). |
Question 2.
Why is the weight of an object on the moon l/6th its weight on the earth?
Answer:
The mass of moon is 1/100 times and its radius 1/4 times that of the earth. As a result, the gravitational attraction on the moon is about one sixth when compared to the earth. Hence, the weight of an object on the moon is l/6th of its weight on the earth.
Page 141
Question 1.
Why is it difficult to hold a school bag having a strap made of a thin and strong string?
Answer:
It is difficult to hold a school bag having a thin strap because the pressure on the shoulders is quite large. This is because the pressure is inversely proportional to the surface area on which the force acts. The smaller the surface area, the larger will be the pressure on the surface. In case of a thin strap, the contact surface area is very small. Hence, the pressure exerted on the shoulder is very large.
Question 2.
What do you mean by buoyancy?
Answer:
The upward force exerted by a liquid on an object immersed in it is known as buoyancy.
Question 3.
Why does an object float or sink when placed on the surface of water?
Answer:
The density of the object and water decides the floating or sinking of the object in water. The density of water is 1g/cm3. An object sinks in water if its density is greater than that of water. An object floats in water if its density is less than that of water.
Page 142
Question 1.
You find your mass to be 42kg on a weighing machine. Is your mass more or less than 42kg?
Answer:
The weighing machine actually measures the mass of the body. Hence, the mass reading of 42kg given by a weighing machine is same as the actual mass of body. As mass is the quantity of inertia, it remains the same.
Question 2.
You have a bag of cotton and an iron bar, each indicating a mass of 100kg when measured on a weighing machine. In reality, one is heavier than the other. Can you say which one is heavier and why?
Answer:
The cotton bag is heavier than the iron bar. The cotton bag experiences larger upthrust of air than the iron bar because it has a larger volume and displaces more air. Hence, in the given situation, cotton is heavier in reality.
JAC Class 9th Science Gravitation Textbook Questions and Answers
Question 1.
How does the force of gravitation between two objects change when the distance between them is reduced to half?
Answer:
According to the universal law of gravitation, the gravitational force of attraction between any two objects of masses say,
M and m, is proportional to the product of their masses and inversely proportional to the square of distance r between them. So, force F is given by
F = \(\mathrm{G} \frac{\mathrm{M} \times \mathrm{m}}{\mathrm{r}^{2}}\)
Now, when the distance r is reduced to half, force between the two masses becomes
F = \(\mathrm{G} \frac{\mathrm{M} \times \mathrm{m}}{\left(\frac{\mathrm{r}}{2}\right)^{2}}\) or F = 4F
Hence, if the distance is reduced to half, the gravitational force becomes four times larger than the previous value.
Question 2.
Gravitational force acts on all objects in proportion to their masses. Why then, a heavy object does not fall faster than a light object?
Answer:
All objects fall on ground with constant acceleration, called acceleration due to gravity (in the absence of air resistance). It is constant and does not depend upon the mass of an object. Hence, heavy objects do not fall faster than light objects.
![]()
Question 3.
What is the magnitude of the gravitational force between the earth and a 1kg object on its surface? (Mass of the earth is 6 × 1024 kg and radius of the earth is 6.4 × 1024 m).
Answer:
Given that,
Mass of the body, m = 1kg
Mass of the earth, M = 6 × 1024 kg
Radius of the earth, R = 6.4 × 106 m
Now, magnitude of the gravitational force (F) between the earth and the body can be given as,
F = \(\mathrm{G} \frac{\mathrm{M} \times \mathrm{m}}{\mathrm{r}^{2}}\) = \(\frac{6.67 \times 10^{-11} \times 6 \times 10^{24} \times 1}{\left(6.4 \times 10^{6}\right)^{2}}\)
= \(\frac{6.67 \times 6 \times 10}{6.4 \times 6.4}\) = 9.8N (approx)
Question 4.
The earth and the moon are attracted to each other by gravitational force. Does the earth attract the moon with a force that is greater or smaller or the same as the force with which the moon attracts the earth? Why?
Answer:
According to the universal law of gravitation, two objects attract each other with equal forces, but in opposite directions. The earth attracts the moon with a force which is equal to the force with which the moon attracts the earth.
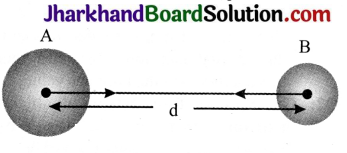
Question 5.
If the moon attracts the earth, why does the earth not move towards the moon?
Answer:
The earth and the moon experience equal gravitational forces from each other. However, the mass of the earth is much larger than the mass of the moon. Hence, it accelerates at a rate lesser than the acceleration rate of the moon towards the earth. For this reason, the earth does not move towards the moon.
Question 6.
What happens to the force between two objects, if
1. the mass of one object is doubled?
2. the distance between the objects is doubled and tripled?
3. the masses of both objects are doubled?
Answer:
- If the mass of one object is doubled, the force between two objects will be doubled (increases).
- If the distance between the objects is doubled, the force between the two objects will be one – fourth and if the distance will be tripled, the force will be one – ninth (1/9).
- If the masses of both objects are doubled, the force will be 4 times.
Question 7.
What is the importance of universal law of gravitation?
Answer:
Universal law of gravitation is important because it tells us about:
- the force that is responsible for binding us to the earth.
- the motion of moon around the earth.
- the motion of planets around the sun.
- the tides formed by rising and falling of water level in the ocean are due to the gravitational force exerted by both the sun and the moon on the earth.
Question 8.
What is the acceleration of free fall?
Answer:
Acceleration of free fall is the acceleration produced when a body falls under the. influence of the force of gravitation of the earth alone. It is denoted by g and its value on the surface of the earth is 9.8 ms-2.
Question 9.
What do we call the gravitational force between the earth and an object?
Answer:
The gravitational force between the earth and an object is called force due to gravity. It is measured as the weight of an object
Question 10.
Amit buys few grams of gold at the poles as per the instruction of one of his friends. He hands over the same when he meets him at the equator. Will the friend agree with the weight of gold bought? If not, why? Hint: The value of g is greater at the poles than at the equator.
Answer:
Weight of a body on the earth is given by W = mg
Where, m = mass of the body, g = acceleration due to gravity.
The value of g is greater at poles than at the equator. Therefore, gold at the equator weighs less than at the poles. ‘Hence, his friend will not agree with the weight of the gold bought.
Question 11.
Why will a sheet of paper fall slower than one that is crumpled into a ball?
Answer:
The sheet of paper will experience a larger air resistance due to its larger surface area than that of its ball form. Hence, the sheet falls slower than its ball form.
Question 12.
Gravitational force on the surface of the moon is only 1/6 as strong as gravitational force on the earth. What is the weight in newton of a 10 kg object on the moon and on the earth?
Answer:
Mass of the object = 10 kg
Weight of the object on the earth = W = m × g
Weight of the object on the moon = 1/6th the weight of an object on the earth Also, acceleration due to gravity, g = 9.8 m/s2
Therefore, weight of a 10 kg object on the earth = 10 × 9.8 = 98 N And, weight of the same object on the moon = \(\frac{1}{6}\) × 98 = 16.3 N.
Question 13.
A ball is thrown vertically upwards with a velocity of 49 m/s. Calculate:
(a) the maximum height to which it rises.
(b) the total time it takes to return to the surface of the earth.
Answer:
(a) According to the equation of motion under gravity:
v2 – u2 = 2gs
Where,
u = initial velocity of the ball
v = final velocity of the ball
s = height achieved by the ball
g = acceleration due to gravity
At maximum height, final velocity of the ball is zero, i.e., v = 0, u = 49 m/s
During upward motion, g = – 9.8 ms-2
Let h be the maximum height attained by the ball. Hence,
0 – (49)-2 = 2 × 9.8 × h
h – \(\frac{49 \times 49}{2 \times 9.8}\) = 122.5m
(b) Let Ttfe the time taken by the ball to reach the height 122.5 m, then according to the equation of motion,
v = u + gt
We get
0 = 49 – (9.8 × t)
∴ 9. 8t = 49 t =\(\frac{49}{9.8}\) = 5s
But, time of ascent = time of descent. Therefore, total time taken by the ball to return = 5 + 5 = 10s.
Question 14.
A stone is released from the top of a tower of height 19.6 m. Calculate its final velocity just before touching the ground.
Answer:
According to the equation of motion under gravity: v2 – u2 = 2gs Where,
u = initial velocity of the stone = 0
v = final velocity of the stone
s = height of the stone = 19.6 mg
g = acceleration due to gravity = 9.8 ms-2
v-2 – 0-2 = 2 × 9.8 × 19.6
v-2 = 2 × 9.8 × 19.6 = (19.6)-2
v = 19.6 ms-1
Hence, the velocity of the stone just before touching the ground is 19.6 ms-1
Question 15.
A stone is thrown vertically upward with an initial velocity of 40 m/s. Taking g = 10 m/s-2, find the maximum height reached by the stone. What is the net displacement and the total distance covered by the stone?
Answer:
According to the equation of motion under gravity: v2 – u2 = 2gs
Where, u = initial velocity of the stone = 40 m/s
v = final velocity of the stone = 0
s = height of the stone
g = acceleration due to gravity = -10 ms-2
Let h be the maximum height attained by the stone.
Therefore, 0 – (40)2 = 2 × (-10) h
⇒ \(\frac{40 \times 40}{20}\) = 80m
Therefore, total distance covered by the stone during its upward and downward journey
= 80 + 80= 160 m
Net displacement of the stone during its upward and downward journey = 80 + (- 80) = 0m
![]()
Question 16.
Calculate the force of gravitation between the earth and the sun, given that the mass of the earth = 6 × 102 kg and of the sun = 2 × 1030 kg. The average distance between the two is 1.5 × 1011 m.
Answer:
According to the question,
M = mass of the sun = 2 × 1030 kg
m = mass of the earth = 6 × 1024 kg
R = average distance between the earth and the sun = 1.5 × 1011 m
From universal law of gravitation, F = \(G \frac{M \times m}{R^{2}}\)
Therefore, putting all the given values in above equation we get;
F = 6.67 × 10-11× \(\frac{\left(6 \times 10^{24}\right) \times\left(2 \times 10^{30}\right)}{\left(1.5 \times 10^{11}\right)^{2}}\)
= 3.56 × 1022 N
Question 17.
A stone is allowed to fall from the top of a tower 100 m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25 m/s. Calculate when and where the two stones will meet.
Answer:
Let ‘t’ be the point at which two stones meet and let ‘h’ be their height from the ground.
It is given that the height of the tower = 100m.
Now, first consider the stone which falls from the top of the tower. So, distance covered by this stone in time t can be calculated using the second equation of motion.
Height covered by the falling stone = s1
s1 = ut + \(\frac{1}{2}\) gt2
s1 = (0 × t) + \(\frac{1}{2}\) gt2
s1 = \(\frac{1}{2}\) gt2 …………(1)
The distance covered by the stone thrown upward = s2
g = – 10 m/s
u = 25 m/s 1
s2 = ut + \(\frac{1}{2}\) gt2
s2 = 25t + \(\frac{1}{2}\) (-g)t2
s2 = 25t – \(\frac{1}{2}\) gt2 ………..(2)
Total height given= 100m
s1 + s1 = 100 m
from equations (1) and (2)
25t + (\(\frac{1}{2}\) gt2 – \(\frac{1}{2}\) gt2) = 100m
25t = 100 m
t = \(\frac{100}{25}\) = 4 seconds …(3)
Putting the value of equation (3) in equation (1), we get
\(\frac{1}{2}\) × 9.8 × 42 = 78.4 m 2
The two stones will meet after 4 seconds when the falling stone has covered a height of 78.4 m and meet the other stone after 4 s at a height = (100 – 78.4)
= 21.6 m from the ground.
Question 18.
A ball thrown up vertically returns to the thrower after 6s. Find:
(a) the velocity with which it was thrown up,
(b) the maximum height it reaches, and
(c) its position after 4s.
Answer:
(a) Time of ascent is equal to the time of descent. The ball takes a total of 6s for its upward and downward journey. Hence, it has taken 3 s to attain the maximum height.
Final velocity of the ball at the maximum height, v = 0
Acceleration due to gravity, g = -9.8 ms-2
Using, equation of motion, v = u + gt
We get, 0 = u + (-9.8 × 3),
u = 9.8 × 3 = 29.4 ms-1
Hence, the ball was thrown upwards with a velocity of 29.4 ms-1
(b) Let the maximum height attained by the ball be ‘h’.
Initial velocity during the upward journey, u = 29.4 ms-1
Final velocity, v = 0
Acceleration due to gravity, g = -9.8 ms-2
From the equation of motion,
s = ut +\(\frac{1}{2}\) at2
h = (29.4 × 3) + (\(\frac{1}{2}\) × (-9.8) × 32)
= 44.1 m
(c) Ball attains the maximum height after 3s. After attaining this height, it will start falling downwards. In this case, initial velocity, u = 0
Position of the ball after 4s of the throw is given by the distance travelled by it during its downward journey in 4s – 3s = 1s.
Equation of motion, s = ut + \(\frac{1}{2}\) gt2
will give,
s = (0 × t) + (\(\frac{1}{2}\) × 9.8 × 12) = 4.9 m
Total height = 44.1 m
This means that the ball is 39.2 m, i.e., (44.1 m – 4.9 m) above the ground after 4 seconds.
Question 19.
In what direction does the buoyant force on an object immersed in a liquid act?
Answer:
The buoyant force on an object immersed in a liquid acts upwards, i.e., opposite to the direction of the force exerted by the object.
![]()
Question 20.
Why does a block of plastic released under water come up to the surface of water?
Answer:
For an object immersed in water, two forces act on it:
- gravitational force, which tends to pull the object in downward direction,
- buoyant force that pushes the object in upward direction. In this case, buoyant force is greater than the gravitational pull on the plastic block.
- This is the reason the plastic block comes up to the surface of the water as soon as it is released under water.
Question 21.
The volume of 50g of a substance is 20 cm3. If the density of water is 1g cm-3 will the substance float or sink?
Answer:
If the density of an object is more than the density of a liquid, it sinks in the liquid. On the other hand, if the density of an object is less than the density of a liquid, it floats on the surface of the liquid.
Here, density of the substance = \(\frac{Mass of the substance}{Volume of the substanc}\) = \(\frac{50}{20}\) = 2.5g cm-3
The density of the substance is more than the density of water (1g cm-3). Hence, the substance will sink in water.
Question 22.
The volume of a 500g sealed packet is 350 cm-3. Will the packet float or sink in water if the density of water is 1g cm-3? What will be the mass of the water displaced by this packet?
Answer:
The density of the 500g sealed packet
= \(\frac{Mass of the packet }{Volume of the packet }\)
= \(\frac{500}{350}\) = 1.428g cm-3
The density of the substance is more than the density of water (1g cm-3). Hence, it will sink in water. The mass of water displaced by the packet is equal to the volume of the packet, i.e., 350 g.