JAC Board Class 9th Science Chapter 11 Notes Work and Energy
→ Work: When a force acts upon an object to cause a change in its position, work is said to be done. It is expressed as the product of force and displacement in the direction of force.
W = F × s
Here, W = work done on the object
F = force on the object
s = displacement of the object
The SI unit of work is newton metre (N m) or joule (J).
1 joule is defined as the amount of work done by a force of 1 N to cause a displacement of 1 m in the object.
![]()
→ Sign Conventions for Work Done
a. When both force and displacement are in the same direction, work done is positive.
W = (F × S)
b. When force acts in a direction opposite to the direction of displacement, the work done is negative.
W = – (F × S)
Angle between force and displacement is 180°.
c. If force and displacement are inclined at an angle less than 180°, the work done is given by:
W = Fs cos θ
where θ is the angle between force and displacement.
d. If force and displacement act at an angle of 90°, the work done is zero.
→ Necessary Conditions for Work to be done
Two conditions are required for the work to be done:
a. A force should act on the object.
b. Object must be displaced.
→ Energy: The capacity of a body to do work is called energy of the body. It is a scalar quantity.
→ Unit of energy: As energy is measured by the amount of work that a body can do, so the unit of energy is same as that of work. The SI unit of energy is joule (J). One joule of energy is the energy required to do 1 J of work.
1 kilojoule = 1 kJ = 1000 J.
→ Forms of energy: The various forms of energy are potential energy, kinetic energy, heat energy, chemical energy, electrical energy and light energy.
→ Kinetic energy: It is the energy possessed by a body by the virtue of its motion. Kinetic energy of an object increases with its speed. Kinetic energy of a body moving with a certain velocity is equal to the work done on it to make it acquire that velocity.
→ Derivation
Let an object of mass’m’, start from rest and attain a uniform velocity ‘v’, after a force ‘F’ is applied on it.
Let, during this period, the object be displaced by a distance ‘s’.
Thus, work done on the object,
W = F × S …(i)
Let the acceleration produced after applying force on the object be ‘a’.
So, using third equation of motion, we have:
v2 – u2 = 2as ……….(ii)
Substituting F and s from equations (ii) and (iii) in equation (i), we get:
W = F × s
W = ma × \(\frac{v^{2}-u^{2}}{2 a}\)
W = \(\frac{1}{2}\)mv2 [As, initial velocity, u = 0]
∴ KE = \(\frac{1}{2}\)mv2
[Work done is stored as kinetic energy]
![]()
→ Potential energy: The energy possessed by a body due to its position, shape or configuration is called its potential energy.
→ Gravitational potential energy (PE): The gravitational potential energy (PE) of an object at a point above the ground is defined as the work done in raising it from the ground to that point, against gravity.
→ Derivation:
Consider a body of mass m, raised through a height ‘h’ from the ground.
Force required to raise the object = weight of the object = mg.
Object gains energy equal to the work done on it.
Work done on the object against gravity is ‘W’.
W = force × displacement = mg × h
W = mgh
PE = mgh
[Work done is stored as potential energy]
→ Mechanical energy:
The sum of kinetic energy and potential energy is called mechanical energy.
→ Law of Conservation of Energy:
It states that energy can neither be created nor destroyed, but it can be transformed from one form to another. The total energy before and after the transformation always remains constant in an isolated system.
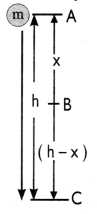
Potential energy + Kinetic energy = Constant (Mechanical energy)
Consider a body of mass ‘m’, raised to a height ‘h’ as shown in the figure. At A, its potential energy is maximum and kinetic energy is 0 as it is stationary.
When body falls at B, ‘h’ is decreasing, hence potential energy decreases. Also, v is increasing, therefore, kinetic energy is increasing.
When the body is about to reach the ground level, h = 0 and ‘v’ will be maximum. Hence, kinetic energy > potential energy.
This shows that decrease in potential energy = increase in kinetic energy.
Thus, there is a continuous transformation of gravitational potential energy into kinetic energy.
![]()
→ Power: The rate of doing work is called power.
Power = \(\frac{\text { Work }}{\text { Time }}\) or P = \(\frac{\mathrm{W}}{\mathrm{t}}\)
Work, power and energy are all scalar quantities.
→ Watt: It is the SI unit of power. The power of an agent is one watt if it does work at the rate of 1 joule per second.
1 watt = \(\frac{1 \text { joule }}{1 \text { second }}\) or 1 W = 1 J s-1
1 kilowatt = 1000 watt or 1 kW = 1000 W
1 horsepower = 746 watt or 1 H.P. = 746 W
→ Kilowatt-hour (kWh): It is the commercial unit of electric energy. It is defined as the electric energy consumed by an appliance of power 1000 watt in one hour.
1 kWh = 3.6 × 106 J