Students should go through these JAC Class 9 Maths Notes Chapter 3 Coordinate Geometry will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 3 Coordinate Geometry
Co-Ordinate System:
In two dimensional coordinate geometry, we generally use two types of coordinate systems.
- Cartesian or Rectangular coordinate system.
- Polar coordinate system.
In cartesian coordinate system we represent any point by ordered pair (x, y) where x and y are called x and y coordinate of that point respectively.
In polar coordinate system we represent any point by ordered pair (r, θ) where is called radius vector and ‘θ’ is called vectorial angle of that point, which will be studied in higher classes.
Cartesian Coordinate System:
→ Rectangular Coordinate Axes:
Let XX’ and YY’ are two lines such that XX’ is horizontal and YY’ is vertical lines in the same plane and they intersect each other at O. This intersecting point is called origin Now choose a convenient unit of length and starting from origin as zero, mark off a number scale on the horizontal line XX’, positive to the right of origin O and negative to the left of origin O. Also mark off the same scale on the vertical line YY’, positive upwards and negative downwards of the origin. The line XX’ is called X-axis and the line YY’ is known as Y-axis and the two lines taken together are called the coordinate axes.
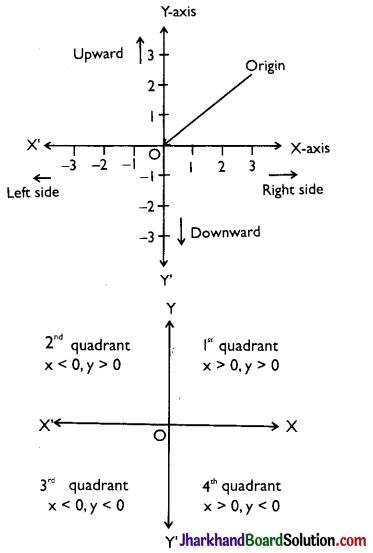
→ Quadrants:
The coordinates axes XX’ and YY’ divide the plane of graph paper into four parts XY, X’Y, X’Y’ and XY’. These four parts are called the quadrants. The parts XY, X’Y, X’Y’ and XY’ are known as the first second, third and fourth quadrants respectively.
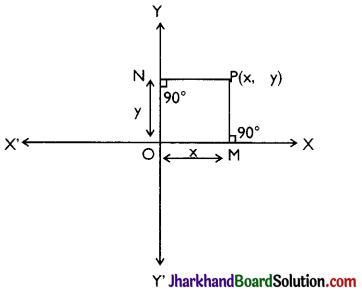
→ Cartesian Coordinates of a Point:
Let -axis and y-axis be the coordinate axes and P be any point in the plane. To find the position of P with respect of x-axis and y-axis, we draw two perpendicular line segment from P on both coordinate axes.
Let PM and PN be the perpendiculars on x-axis and y-axis resepectively. The length of the line segment OM is called the x-coordinate or abscissa of point P. Similarly the length of line segment ON is called the y-coordinate or ordinate of point P.
Let OM = x and ON = y. The position of the point P in the plane with respect to the coordinate axes is represented by the ordered pair (x, y). The ordered pair (x, y) is called the coordinates of point P. “Thus, for a given point, the abscissa and ordinate are the distances of the given point from y-axis and x-axis respectively”.
The above system of coordinating of ordered pair (x, y) with every point in plane is called the Rectangular or Cartesian coordinate system.
Cartesian coordinate system
![]()
→ Convention of Signs:
As discussed earlier that regions XOY, Χ’ΟΥ, Χ’ΟΥ’ and ΧΟΥ’ are known as the first second, third and fourth quadrants respectively. The ray OX is taken as positive X-axis, OX’ as negative x-axis, OY as positive y-axis and OY as negative y-axis. Thus we have.
In first quadrant: x > 0, y > 0
In second quadrant: x < 0, y > 0
In third quadrant: x < 0, y < 0
In fourth quadrant: x > 0, y < 0
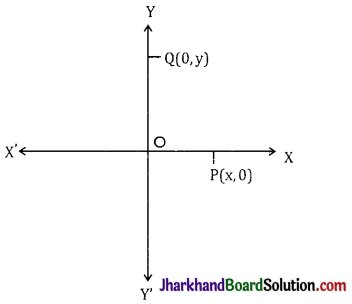
→ Points on Axis:
If point P lies on x-axis then clearly its distance from x-axis will be zero, therefore we can say that its ordinate will be zero. In general, if any point lies on x-axis then its y-coordinate will be zero. Similarly if any point Q lies on y-axis, then its distance from y-axis will be zero therefore we can say its x-coordinate will be zero. In general, if any point lies on y-axis then its x-coordinate will be zero.
→ Plotting of Points:
In order to plot the points in a plane, we may use the following algorithm.
Step I: Draw two mutually perpendicular lines on the graph paper, one horizontal and other vertical.
Step II: Mark their intersection point as O (origin).
Step III: Choose a suitable scale on X-axis and Y-axis and mark the points on both the axes.
Step IV: Obtain the coordinates of the point which is to be plotted. Let the point be P(a, b). To plot this point start from the origin and |a| units move along OX, OX’ according as ‘a’ is positive or negative respectively. Suppose we arrive at point M. From point M move vertically upward or downward |b| units according as ‘b’ is positive or negative respectively The point where we arrive finally is the required point P(a, b).
Distance Between Two Points:
→ If there are two points A (x1, y1) and B(x2, y2) on the XY plane, the distance between them is given by
AB = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)