Students should go through these JAC Class 9 Maths Notes Chapter 6 Lines and Angles will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 6 Lines and Angles
Line:
A line has length but no width and no thickness.
Angle:
An angle is formed by two non-collinear rays with a common initial point. The common initial point is called the ‘vertex’ of the angle and two rays are called the ‘arms’ of the angle.
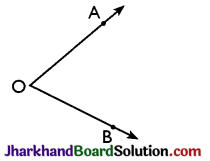
Remark:
Every angle has a measure and unit of measurement is degree. One right angle = 90°
1° = 60′ (minutes)
1′ = 60″ (seconds)
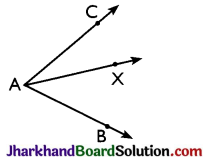
Angle addition axiom: If X is a point in the interior of BAC, then
∠BAC = ∠BAX + ∠XAC
Types of Angles:
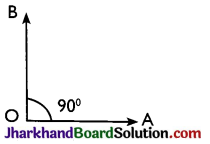
→ Right angle: An angle whose measure is 90° is called a right angle.
→ Acute angle: An angle whose measure is more than 0° but less than 90° is called an acute angle.
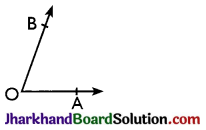
0° < ∠BOA < 90°
→ Obtuse angle: An angle whose measure is more than 90° but less than 180° is called an obtuse angle.

90° < ∠AOB < 180°
→ Straight angle: An angle whose measure is 180° is called a straight angle.

→ Reflex angle: An angle whose measure is more than 180° but less than 360 is called a reflex angle.
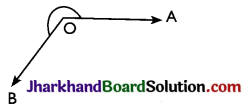
180° < ∠AOB < 360°
→ Complementary angles: Two angles whose sum is 90° are called complementary angles.
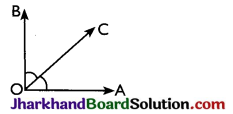
∠AOC and ∠BOC are complementary as
∠AOC + ∠BOC = 90°
→ Supplementary angles: Two angles whose sum is 180° are called the supplementary angles.
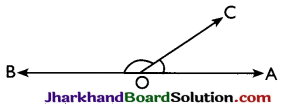
∠AOC and ∠BOC are supplementary as their sum is 180°.
→ Angle bisectors: A ray OX is said to be the bisector of ∠AOB, if X is a point in the interior of ∠AOB, and ∠AOX = ∠BOX
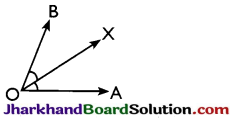
→ Adjacent angles: Two angles are called adjacent angles if
→ they have the same vertex,
→ they have a common arm,
→ non-common arms are on either side of the common arm.
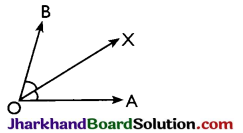
∠AOX and ∠BOX are adjacent angles as o is the common vertex, OX is common arm, OA and OB are non-common arms and lie on either side of OX.
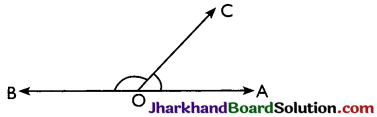
→ Lincar pair of angles: Two adjacent angles are said to form a linear pair if their non-common arms are two opposite rays.
→ Vertically opposite angles: Two angles are called a pair of vertically opposite angles, if their arms form two pairs of opposite rays.
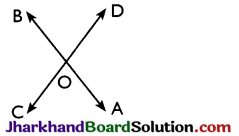
∠AOC and ∠BOD form a pair of vertically opposite angles. Also ∠AOD and ∠BOC form a pair of vertically opposite angles.
![]()
Angles Made by a Transversal with two Parallel Lines:
→ Transversal: A line which intersects two or more given lines at distinct points is called a transversal of the given lines
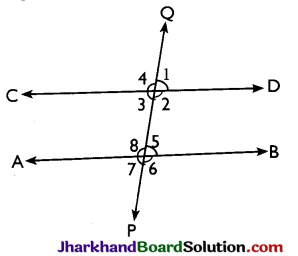
→ Corresponding angles: Two angles on the same side of transversal are known as the corresponding angles if both lie either above the two lines or below the two lines, in figure 1 and 5, 4 and 8, 2 and 6, 3 and 7 are the pairs of corresponding angles.
→ Alternate interior angles: ∠3 and ∠5, ∠2 and ∠8, are the pairs of alternate interior angles.
→ Consecutive interior angles: The pair of interior angles on the same side of the transversal are called pair of consecutive interior angles. In figure ∠2 and ∠5, ∠3 and ∠8. are the pairs of consecutive interior angles.
→ Corresponding angles axiom: If a transversal intersects two parallel lines, then each pair of corresponding angles are equal. Conversely, if a transversal intersects two lines, making a pair of equal corresponding angles, then the lines are parallel.
Important Facts to Remember:
→ If a ray stands on line, then the sum of the adjacent angles so formed is 180°.
→ If the sum of two adjacent angles is 180°, then their non-common arms are two apposite rays.
→ The sum of all the angles round a point is equal to 360°.
→ If two lines intersect, then the vertically opposite angles are equal.
→ If a transversal interests two parallel lines then the corresponding angles are equal, each pair of alternate interior angles is equal and each pair of consecutive interior angles is supplementary.
→ If a transversal intersects two lines in such a way that a pair of alternate interior angles are equal, then the two lines are parallel.
→ If a transversal intersects two lines in such a way that a pair of consecutive interior angles are supplementary, then the two lines are parallel.
→ If two parallel lines are intersected by a transversal, the bisectors of any pair of alternate interior angles are parallel and the bisectors of any two corresponding angles are also parallel.
→ If a line is perpendicular to one of the two given parallel lines, then it is also perpendicular to the other line.
→ Two angles which have their arms parallel are either equal or supplementary.
→ Two angles whose arms are perpendicular are either equal or supplementary.
Important Theorems:
Theorem 1.
If two lines intersect each other, then the vertically opposite angles are equal.
Proof:
Given: Two lines AB and CD intersecting at a point O.
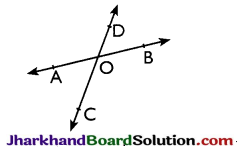
To prove: ∠AOC = ∠BOD, ∠BOC
= ZAOD
Proof: Since ray OD stands on AB
again, ray OA stands on CD
⇒ ∠AOD + ∠DOB = 180° [linear pair] ……(i)
⇒ ∠AOC + ∠AOD = 180° [linear pair] ……(ii)
From equations (i) and (ii), we get
∠AOD + ∠DOB
= ∠AOC + ∠AOD
⇒ ∠AOC = ∠DOB
Similarly, we can prove that
∠BOC = ∠DOA Hence, proved.
![]()
Theorem 2.
If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.
Proof:
Given: AB and CD are two parallel lines. Transversal l intersects AB and CD at P and Q respectively making two pairs of alternate interior angles, ∠1, ∠2 and ∠3, ∠4.
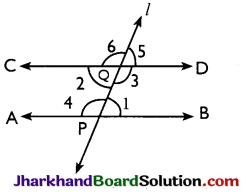
To prove: ∠1 = ∠2 and ∠3 = ∠4
Proof: Clearly, ∠2 = ∠5 [Vertically opposite angles]
And, ∠1 = ∠5 [Corresponding angles]
∴ ∠1 = ∠2
Also, ∠3 = ∠6 [Vertically opposite angles]
And, ∠4 = ∠6 [Corresponding angles]
∴ ∠3 = ∠4 Hence, proved.