JAC Class 9 Science Important Questions Chapter 11 Work and Energy

JAC Board Class 9th Science Important Questions Chapter 11 Work and Energy

Multiple Choice Questions

Question 1.
The gravitational potential energy of an object is due to
(a) it’s mass
(b) its acceleration due to gravity
(c) its height above the earth’s surface
(d) all of the above
Answer:
(d) all of the above

Question 2.
The unit of work is the joule. The other physical quantity that has the same unit is
(a) power
(b) velocity
(c) energy
(d) force
Answer:
(c) energy

Question 3.
If the velocity of a body is doubled, its kinetic energy
(a) gets doubled
(b) becomes half
(c) does not change
(d) becomes 4 times
Answer:
(d) becomes 4 times

Question 4.
A student carries a bag weighing 5 kg from the ground floor to his class on the first floor that is 2 m high. The work done by the boy is
(a) 1J
(b) 10J
(c) 100J
(d) 1000J
Answer:
(c) 100J

Question 5.
How much time will be required to perform 520 J of work at the rate of 20 W?
(a) 24s
(b) 16s
(c) 20s
(d) 26s
Answer:
(d) 26s

Question 6.
A body of mass 2 kg is dropped from a height of lm. Its kinetic energy as it touches the ground is
(a) 19.6N
(b) 19.6J
(c) 9.8m
(d) 9.8J
Answer:
(b) 19.6J

Question 7.
The unit of power is
(a) watt per second
(b) joule
(c) kilojoule
(d) joule per second
Answer:
(d) joule per second

Question 8.
A coolie carries a load of 500 N to a distance of 100 m. The work done by him is
(a) 5 Nm
(b) 50,000 Nm
(c) 0 Nm
(d) 1/5 N m
Answer:
(c) 0 Nm

Question 9.
Power is a measure of the
(a) rate of change of momentum
(b) force which produces motion
(c) change of energy
(d) rate of change of energy
Answer:
(d) rate of change of energy

Question 10.
If the speed of an object is doubled, its kinetic energy is
(a) doubled
(b) quadrupled
(c) halved
(d) tripled
Answer:
(b) quadrupled

Question 11.
Which of the following is not correct?
(a) Energy is the ability of doing work
(b) Work can be expressed as F × s
(c) Unit of power is joule
(d) Power is the amount of work done per unit of time
Answer:
(d) Power is the amount of work done per unit of time

Question 12.
kW h is the unit of
(a) acceleration
(b) work
(c) power
(d) energy
Answer:
(c) power

Question 13.
Considering air resistance negligible, the sum of potential and kinetic energies of a free falling body would be
(a) zero
(b) increasing
(c) decreasing
(d) fixed
Answer:
(d) fixed

Question 14.
Two bodies of masses m] and m2 have equal kinetic energies. If P₁ and P₂ are their respective momenta, the ratio of P₁ to P₂ is
(a) m₁ : m₂
(b) m₂ : m₁
(c) \(\sqrt{\mathrm{m}_{1}} : \sqrt{\mathrm{m}_{2}}\)
(d) \(m_{1}^{2} : m_{2}^{2}\)
Answer:
(c) \(\sqrt{\mathrm{m}_{1}} : \sqrt{\mathrm{m}_{2}}\)

Question 15.
A light and a heavy body have equal momenta Which one has greater kinetic energy?
(a) The lighter body
(b) The heavier body
(c) Both have same KE
(d) None of these
Answer:
(b) The heavier body

Analysing & Evaluating Questions

Question 16.
A car is accelerated on a levelled road and attains a velocity four times of its initial velocity. In this process the potential energy of the car
(a) does not change
(b) becomes twice to that of initial
(c) becomes 4 times that of intial
(d) becomes 16 times that of initial
Answer:
(a) does not change

Question 17.
An iron sphere of mass 10 kg has the same diameter as an aluminium sphere of mass 3.5 kg. Both spheres are dropped simultaneously from a tower. When they are 10 m above the ground, they have the same
(a) acceleration
(b) momenta
(c) potential energy
(d) kinetic energy
Answer:
(a) acceleration

Question 18.
A girl is carrying a school bag of 3 kg mass on her back and moves 200 m on a levelled road. The work done against the gravitational force will be (g = 10 m^-2)
(a) 6 × 10³J
(b) 6J
(c) 0.6J
(d) zero
Answer:
(d) zero

Assertion Reason Questions

Directions: In the following questions, the Assertions and the Reasons have been put forward. Read the statements carefully and choose the correct alternative from the following:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.
(B) The assertion and the reason are correct but the reason is not the correct explanation of the assertion.
(C) The assertion is true but the reason is false.
(D) Both the statements are false.
1. Assertion: Work, the product of force and displacement, is a vector quantity.
Reason: Product of two vector quantities is always a vector quantity.
Answer:
(D) Both the statements are false.

2. Assertion: When a book is moved from a table to the top of an almirah, its potential energy increases.
Reason: Higher the height of a body from the ground level, higher is its potential energy.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.

3. Assertion: A person carrying a suitcase on his head is not doing any work. Reason: The force applied by the person is acting in the downward direction.
Answer:
(C) The assertion is true but the reason is false.

4. Assertion: The work done by the force of gravity on the moon revolving around the earth is zero.
Reason: The gravitational force and the displacement of moon are at right angles to each other.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.

5. Assertion: Work done on an object can be positive, negative or zero.
Reason: Work done is a scalar quantity.
Answer:
(B) The assertion and the reason are correct but the reason is not the correct explanation of the assertion.

Very Short Answer Type Questions

Question 1.
Define work.
Answer:
Work is said to be done when a force applied on a body produces a displacement of the body. It is given by W = F x s where ‘F’ is the force applied and ‘s’ is the displacement caused.

Question 2.
State reason why work is a scalar quantity.
Answer:
Work is the product of force (F) and displacement (s). Since both F and s are vector quantities and the dot product of vector quantities produces a scalar quantity, therefore, work is a scalar quantity.

Question 3.
Name two kinds of potential energies.
Answer:
Gravitational potential energy and elastic potential energy.

Question 4.
If the work done is 20J and displacement is 2m, find the force applied.
Answer:
Given, W = 20J and s = 2m.
W = F × s
20 = F × 2
F= 10 N

Question 5.
Name the energy stored in a rubber band when it is stretched?
Answer:
On stretching a rubber band, potential energy is stored in it.

Question 6.
State the law of conservation of energy.
Answer:
It states that energy can neither be created nor destroyed. It can only change its form.

Question 7.
When a book is lifted from a table, against which force is the work done?
Answer:
Work is done against the force of gravity.

Question 8.
Define the commercial unit of energy.
Answer:
The commercial unit of energy is kW h (kilowatt hour). 1 kW h is the energy used in one hour at the rate of 1000 J per second.
1 kWh = 1 kW × 1 h = 3.6 × 10⁶j

Question 9.
A light and a heavy body have equal kinetic energies. Which one is moving faster?
Answer:
The lighter body is moving faster because for the same kinetic energy, velocity is inversely proportional to the mass.
Analysing & Evaluating Question uestions

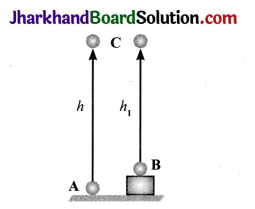
Question 10.
Two objects of same mass are placed at positions A and B as shown in the figure. Both of them are raised to the position C. In which case, the potential energy is more?
Answer:
The object at A will gain more potential energy than the object at B. But the final potential energy of both A and B will be equal when raised to position C.

Question 11.
A rocket is moving up with a velocity v. If the velocity of this rocket is suddenly tripled, what will be the ratio of the itwo kinetic energies?
Answer:
K.E. °c (velocity)²
When the velocity is tripled, K.E. increases by a factor of 9 ( = 3²)
Thus, the ratio of the two kinetic energies is 1 : 9.

Question 12.
Can any object have momentum even if its mechanical energy is zero? Explain.
Answer:
No. Zero mechanical energy means no potential energy and no kinetic energy. Zero kinetic energy means, zero velocity. As a result, momentum is also zero (as P = mv).

Short Answer Type Questions

Question 1.
Calculate the work done by a man in rotating a wheel of an amusement slide in a fair 40 times in 1 minute?
Answer:
The man is rotating the wheel of an amusement slide by just standing at a place. This concludes that the wheel is not undergoing any displacement. Since displacement is zero, therefore, work done is zero.

Question 2.
Define positive work done and negative work done.
Answer:

1. Positive work (done: Work done is positive when the displacement occurs in the direction of force.
2. Negative work done: Work done is negative when the displacement occurs opposite to the direction of force.

Question 3.
In which of the following cases, work is said to be done?
1. When we push a table and the table is displaced.
2. When a person holds a book in his hand and keeps it stationary.
3. When a wire is twisted.

Answer:

1. When we push a table and the force applied by us is large enough to move it from its original position, then work is said to be done.
2. When a person holds a book in his hand and keeps it stationary, there occurs no movement of the book. In this case, though a force is constantly being applied, there is no displacement and hence work done is zero.
3. When a wire is twisted, the shape of the wire changes which concludes that work is done as there occurred changes in the configuration of the wire.

Question 4.
What will be the nature of work done when the force acting on a body retards its motion? Justify your answer by quoting examples.
Answer:
When force retards the motion of a body, the motion is stopped, i.e., a force opposite to the direction of the motion is applied. Thus, a negative work is done by the force.
For example:

1. In tug of war, the work done by the losing team is negative.
2. When a ball is thrown up in the air, the gravitational force acting downwards upon the ball does negative work on the ball.

Question 5.
What is gravitational potential energy?
Answer:
The gravitational potential energy of an object at a point above the ground
is defined as the work done in raising an object from the ground to that point against gravity.
G_PE = mgh

Question 6.
Differentiate between potential energy and kinetic energy.
Answer:

Potential Energy	Kinetic Energy
(a) Energy possessed by a body due to its position, shape or configuration.	(a) Energy possessed by a body due to its motion.
(b) P.E. = mgh where, m = mass, g = acceleration due to gravity, h = height.	(b) K.E. = \(\frac{1}{2}\) mv2 where, m = mass, v = velocity.

Question 7.
State two situations where energy is supplied but no work is done.
Answer:
(a) A person pushing a heavy rock is using all the energy but if the rock does not move, no work is done, (b) A person standing with heavy load on his head is spending energy in doing this, but no work is done.

Question 8.
How are work and energy related to each other?
Answer:
An object having a capability to do work is said to possess energy. The object which does work loses energy and the object on which work is done, gains energy. The unit of both energy and work is joule.

Question 9.
On what factor does the gravitational potential energy depend?
Answer:
Gravitational potential energy depends on the height of object from the ground level zero level we choose. Example: A ball tossed from the second floor of a building will attain a height, say h, from its roof, but from the first floor its height will be h ‘where h > h’.
Hence, the potential energy of the ball on the first floor level is less as compared to that on the second floor.

Question 10.
Write the form of energy possessed by the body in the following situations:
(a) A coconut falling from tree
(b) An object raised to a certain height
(c) Blowing wind
(d) A child driving a bicycle on the road
Answer:
(a) Kinetic energy + Potential energy
(b) Potential energy
(c) Kinetic energy
(d) Kinetic energy

Question 11.
What is energy? Give the unit of energy. Name the different forms of energy.
Answer:
Energy of a body is defined as its capacity or ability to do work. When a body is capable of doing more work, it is said to possess more energy.
The SI unit of energy is joule (J).
Energy has many forms: potential energy, kinetic energy, heat energy, chemical energy, electrical energy, light energy, solar energy, etc.

Question 12.
Derive an equation for kinetic energy of an object?
Answer:
The kinetic energy of a body can be determined by calculating the amount of work required to set the body into motion with the velocity ‘v’ from its state of rest. Suppose,
m = mass of the body
u = 0 = initial velocity of the body
F = force applied on the body
a = acceleration produced in the body in
the direction of force
v = final velocity of the body
s = distance covered by the body
As v² – u² = 2as
= v² – 0² = 2as
a= \(\frac{v^{2}}{2 s}\)
As the force and displacement are in the same direction, the work done on the body is
W = Fs = mas = m \( \frac{\mathrm{v}^{2}}{2 \mathrm{~s}}\)s = \(\frac{1}{2}\) mv²
This work done appears as the kinetic energy of the body.
∴ KE = \(\frac{1}{2}\) mv²

Question 13.
Derive an equation for potential energy?
Answer:
Let the work done on the object against gravity be W.
Work done, W = force × displacement
Work done, W = mg × h
Work done, W = mgh
Since work done on the object is equal to mgh, an energy equal to mgh units is gained by the object. This is the potential energy (E_p) of the object.
E_p = mgh

Question 14.
An electric heater of 1000 W is used for 2 hours a day. What is the cost of using it for a month of 28 days, if 1 unit costs ₹ 3.00?
Answer:
Here, P = 1000W = lkW
Total time, t = 2 × 28 hours = 56 hours
Total energy consumed = P × t
= 1 kW × 56 h = 56 kW h
Cost of 1 kWh = ₹ 3.00
Cost of 56 kWh = 3 × 56 = ₹ 168.

Analysing & Evaluating Questions

Question 15.
Two identical pointed objects made from iron and wood are allowed to fall on a heap of sand from the same height. The iron object penetrates more in sand than the wooden object. Which of the objects has more potential energy?
Answer:
Of the two identical objects, the one made from iron will have greater mass. So when it falls from a height, it will possess greater kinetic energy as compared to the wooden object. As a result,
(a) the iron object will penetrate more in sand.
(b) the iron object will have more potential energy.

Question 16.
The weight of a person on a planet A is about half that on the earth. He can jump upto 0.4 m height on the surface of the earth. How high can he jump on the planet A?
Answer:
The weight of a person on planet A is about half that on the earth. This means, the acceleration due to gravity of the planet A is half that of the earth. So, Height of the jump on the surface of planet A = \(\frac{0.4 \mathrm{~m}}{1 / 2}\) = 0.8 m

Long Answer Type Questions

Question 1.
How is work done measured when a body moves in a direction inclined to the direction of the applied force?
Answer:
In the figure, a force F pulls a block making angle 0 with the horizontal surface. Under this force, suppose the block moves from position A to B after covering a distance ‘s’.

Let, F₁ = Component of force in the direction of displacement ‘s’
Then, \(\frac{F_{1}}{F}\) = cos θ or F₁ = F cos θ
Work done = Component of force in the direction of displacement × displacement
W = F₁ × s = F cos θ x s
W = Fs cos θ
Special cases:
(a) When θ = 0°,
cos θ = 1 and W = Fs
Thus, work done is maximum when the displacement of the body is along the direction of the force.

(b) When θ = 90°,
cos θ = 0 and W = 0
Thus, work done is zero when the displacement of the body is perpendicular to the direction of force.

(c) When θ = 180°,
cos θ = -1 and W = – Fs
Thus, work done is negative when displacement is opposite to the direction of force.

(d) When s = 0, W = 0 Thus, work done on a stationary body is zero.

Question 2.
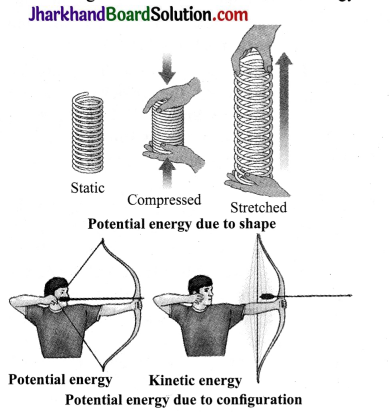
What is meant by potential energy of a body? Give some examples.
Answer:
The energy possessed by a body by the virtue of its position, shape or configuration is called its potential energy.

1. Examples of P.E. due to position:
   • Water stored in a dam at a height has potential energy.
   • A stone lying on the roof of the building has potential energy.
2. Examples of P.E. due to shape:
   • In a toy car, the wound spring possesses potential energy. As the spring is released, its potential energy changes into kinetic energy which moves the toy car.
   • Energy possessed by a stretched rubber band is potential energy.
3. Example of P.E. due to configuration:
   • A stretched bow possesses potential energy. As soon as it is released, it shoots the arrow in the forward direction with a large velocity.
   • The potential energy of the stretched bow gets converted into the kinetic energy of the arrow.
     

Question 3.
A 100 W electric bulb is lighted for 2 hours every day and five 40 W tubes are lighted for 4 hours every day. Calculate:
(a) the energy consumed for 60 days and
(b) the cost of electricity consumed at the rate of ₹3 per kW h.
Answer:
(a) Energy consumed by a 100 W bulb each day = 100 W × 2 h
= 200 Wh = \(\frac{200}{1000}\)= 0.2 kW h
Energy consumed by five 40 W tubes each day = 5 × 40 W × 4h
= 800 Wh = \(\frac{800}{1000}\) = 0.8 kW h
Total energy consumed each day = 0.2 + 0.8 = 1.0 kWh
Total energy consumed in 60 days = 1.0 x 60 = 60 kWh

(b) Cost of 1 kW h = ₹ 3
Cost of 60 kW h = 3 × 60 = 180

Question 4.
Answer the following:
(a) List any three situations in your daily life where you can say that work has been done.
(b) How much work is done in increasing the velocity of a car from 15 km/h to 30 km/h if the mass of the car is 1000 kg?
Answer:
(a) Three situations where work is done are:

1. Pushing a pebble lying on the ground. The pebble moves through some distance. Here, we apply a force and the pebble gets displaced. So, we have done work on the pebble.
2. We apply a force to lift a book through a height. The book rises up. We have done work in moving up the book.
3. A bullock is pulling a cart and the cart moves. There is a force on the cart and the cart has moved. The bullock has done work on the cart.

(b) According to the question,
u = 15 km/h = 4 m/s
v = 30 km/h = 8 m/s
Mass = 1000 kg
W = ?
W = K.E. = \(\frac{1}{2}\) m(v² – u²)
\(\frac{1}{2}\) × 1000 × ((8)² – (4)²)
= \(\frac{1}{2}\) × 1000 × (64 – 16)
= \(\frac{1}{2}\) × 1000 × (675) = 24,000J
Hence, work done is 24,000J.

Analysing & Evaluating Questions

Question 5.
A boy is moving on a straight road against a frictional force of 5N. After traveling a distance of 1.5 km he forgot the correct path at a roundabout of radius 100 m. However, he moves on that circular path for one and half cycle and then he moves forward up to 2.0 km. Calculate the work done by him.
Answer:
Work done by the boy while moving on a straight road
W = F × s
W = 5N × 1.5 km
= 5 kg m s^-2 × 1500 m = 7500J
Work done during moving around circular path
= 5N × (2 × 100 m) = 1000J
Work done during moving further by
2.0 km = 5N × (2 × 1000 m) = 10,000J
Total work done by the boy = 7500J + 1000J + 10,000J
= 18500J

Activity 1

• Take a heavy ball. Drop it on a thick bed of sand. A wet bed of sand would be better. Drop the ball on the sand bed from a height of about 25 cm and observe the results.
• Repeat this activity from heights of 50 cm, lm and 1.5 m.
• Ensure that all the depressions are distinctly visible.
• Mark the depressions to indicate the height from which the ball was dropped.
• Compare their depths.

Observations

• The ball that falls from the height of 1.5 m creates the deepest depression.
• The ball that falls from the height of 50 cm creates the shallowest depression.
• Larger the height from which the ball is dropped, larger is the kinetic energy gained by the ball on reaching the ground and more is its capability of doing work.

Activity 2

1. Set up the apparatus as shown in the figure.
2. Place a wooden block of known mass in front of the trolley at a convenient fixed distance.
3. Place a known mass on the pan so that the trolley starts moving.
4. The trolley moves forward and hits the wooden block.
5. Fix a stop on the table in such a manner that the trolley stops after hitting the block. The block gets displaced.
6. Note down the displacement of the block.
7. Repeat this activity by increasing the mass on the pan. Observe, in which case is the displacement more.
   

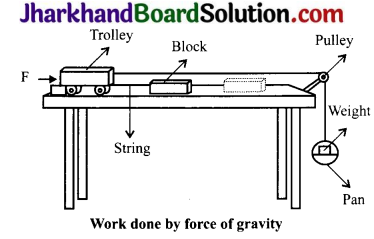
Observations

1. The force of gravity pulls the mass in the pan in the downward direction. This force gets transferred to the trolley through the string.
2. The trolley moves and hits the block with a force.
3. The larger the mass in the pan, the larger is the force with which the trolley hits the block.
4. Consequently, larger will be the displacement and larger will be the work done. The moving trolley possess energy and hence does work on the block.

Activity 3

• Take a slinky as shown below.
• Ask a friend to hold one of its ends. You hold the other end and move away from your friend. Now, you release the slinky and observe.
  

Observations

• When released, the slinky regains its original length. The slinky has acquired potential energy due to the work done on it during stretching. On releasing, potential energy is converted into kinetic energy.
• The slinky will also acquire energy when it is compressed.

Value Based Questions

Question 1.
Apoorva saw few planter pots kept on the balcony sill of fourth floor in her building. She makes an effort and keeps all the planter pots down the sill.
1. What type of energy is present in the pot kept on the balcony sill of fourth floor?
2. If the pot falls from the fourth floor, what type of energy will be seen in the falling pot?
3. What value of Apoorva is reflected in the above act?
Answer:
1. The pot on the sill possesses potential energy.
2. The falling pot possesses both the kinetic energy and the potential energy.
3. Apporva showed the value of moral responsibility and awareness.

Question 2.
Siddharth saw a lady labourer who carried bricks on her head from one point of the construction site to the other end which was some 500 m away. He prepares a trolley for the labourer to carry the bricks to make her work easier.
1. In carrying the bricks from point A to point B on the head by the lady labourer in the construction site, is any work done by the labourer?
2. By pulling the trolley of bricks from point A to point B, is any work done?
3. What value of Siddharth is seen in the above act?
Answer:
1. In carrying the bricks from point A to point B on head by the lady, no work is said to be done.
2. By pulling the trolley of bricks, work is said to be done.
3. Siddharth showed kindness, general awareness and sympathy.

JAC Class 9 Science Important Questions