JAC Board Class 9th Science Important Questions Chapter 8 Motion
Multiple Choice Questions
Question 1.
Which of the following is correct for a car which travels a distance of 100 km in 2 hours?
(a) Its average speed is 50 km/h
(b) The car did not travel at 50 km/h all the time
(c) The car travelled at 50 km/h all the time
(d) All of the above
Answer:
(a) Its average speed is 50 km/h
Question 2.
The distance-time graph of an object shown in the given figure represents that the object is
(a) at rest position
(b) moving with constant speed
(c) moving with constant velocity
(d) moving with constant acceleration
Answer:
(a) at rest position
Question 3.
The SI unit of velocity is
(a) ms-1
(b) ms-2
(c) ms-3
(d) Nn-1
Answer:
(a) ms-1
Question 4.
Deceleration of a body is expressed in
(a) m
(b) ms-1
(c) ms-2
(d) ms-3
Answer:
(c) ms-2
![]()
Question 5.
The initial velocity of a body is ‘u’. It is under uniform acceleration ‘a’. Its velocity ‘v’ at any time ‘t’ is given by
(a) v = u + at2
(b) v = u + \(\frac{1}{2}\) at2
(c) v = u + at
(d) v = u
Answer:
(c) v = u + at
Question 6.
A wooden slab starting from rest, slides down a 10m long inclined plane with an acceleration of 5 ms-2 What would be its speed at the bottom of the inclined plane?
(a) 10 ms-1
(b) 12ms-1
(c) 10 cm-1
(d) 12 cm-1
Answer:
(a) 10 ms-1
Question 7.
The velocity of a particle increases from ‘u’ to ‘v’ in time’t’ during which it covers a distance ‘s’. If the particle has a uniform acceleration, which of the following equations does not apply to the motion?
(a) 2s = (v + u) t
(b) v2 = u2 – 2as
(c) a = v – u/t
(d) s = (u + \(\frac{1}{2}\) at) t
Answer:
(b) v2 = u2 – 2as
Question 8.
In 12 minutes, a car whose speed is 35 km/h travels a distance of
(a) 7 km
(b) 3.5 km
(c) 2.4 km
(d) none of these
Answer:
(a) 7 km
Question 9.
The area under the distance – time graph gives
(a) uniform speed
(b) non – uniform speed
(c) velocity and speed
(d) both (a) and (b)
Answer:
(d) both (a) and (b)
Question 10.
The odometer of a car measures
(a) speed
(b) velocity
(d) acceleration
(d) distance
Answer:
(d) distance
Question 11.
If a particle moves with a constant speed, the distance time graph is a
(a) straight line
(b) curved line
(c) straight line parallel to time axis
(d) straight line parallel to velocity axis
Answer:
(a) straight line
Question 12.
An object moving with uniform circular motion shows
(a) constant acceleration in speed
(b) constant velocity
(c) constant acceleration in direction
(d) constant change in type of motion
Answer:
(c) constant acceleration in direction
Question 13.
The slope of speed – time graph gives
(a) speed
(b) velocity
(c) acceleration
(d) momentum
Answer:
(c) acceleration
Question 14.
The distance travelled by a freely falling body is proportional to the
(a) mass of body
(b) square of the time of fall
(c) square of the acceleration due to
Answer:
(b) square of the time of fall
![]()
Question 15.
The figure shows the displacement time graph of a body moving in a straight line. The velocity of the body during the
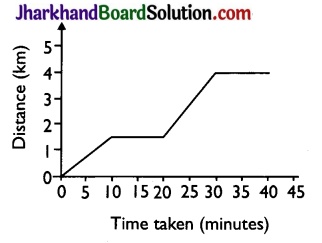
(a) 2 ms-2
(b) zero
(c) 3 ms-1
(d) 2.5 ms-1
Answer:
(b) zero
Analysing & Evaluating Questions
Question 16.
In which of the following cases of motion, the distance moved and the magnitude of displacement are equal?
(a) If the car is moving on a straight road
(b) If the car is moving in a circular path
(c) The pendulum is moving to and fro
(d) The earth is revolving around the Sun
Answer:
(a) If the car is moving on a straight road
Question 17.
Four cars A, B, C and D are moving on a levelled road. Their distance versus time graphs are shown here. Choose the correct statement.
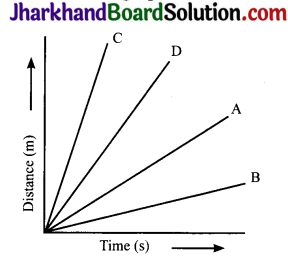
(a) Car A is faster than car D
(b) Car B is the slowest
(c) Car D is faster than car C
(d) Car C is the slowest
Answer:
(b) Car B is the slowest
Question 18.
Suppose a boy is enjoying a ride on a merry – go – round which is moving with a constant speed of 10 ms-1. It implies that the boy is
(a) at rest
(b) moving with no acceleration
(c) in accelerated motion
(d) moving with uniform velocity
Answer:
(c) in accelerated motion
Assertion Reason Questions
Directions: In the following questions, the Assertions and the Reasons have been put forward. Read the statements carefully and choose the correct alternative from the following:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.
(B) The assertion and the reason are correct but the reason is not the correct explanation of the assertion.
(C) The assertion is true but the reason is false.
(D) Both the statements are false.
1. Assertion: Velocity is a scalar quantity.
Reason: Velocity cannot be zero.
Answer:
(D) Both the statements are false.
2. Assertion: A body moving in a circular path is in non – uniform motion.
Reason: The direction of a body moving in a circular path changes at every point.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.
3. Assertion: A stone thrown vertically upwards has negative acceleration.
Reason: The acceleration of the stone thrown upward is in the direction opposite to the direction of its motion.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.
4. Assertion: A freely falling body is in uniform motion.
Reason: A freely falling body covers equal distances in equal intervals of time.
Answer:
(D) Both the statements are false.
5. Assertion: An object under acceleration can have a uniform speed.
Reason: Both speed and acceleration are scalar quantities.
Answer:
(C) The assertion is true but the reason is false.
Very Short Answer Type Questions
Question 1.
Define uniform motion.
Answer:
If an object covers equal distances in equal intervals of time, however small the time intervals may be, the motion of the object is said to be uniform motion.
Question 2.
Define non – uniform motion.
Answer:
If an object covers unequal distances in equal intervals of time, it is said to be in ‘non – uniform motion’.
Question 3.
Define speed.
Answer:
It is the distance travelled by a body per unit time.
Speed. = \(\vec{a}\)
Question 4.
Define average speed.
Answer:
The total distance travelled by an object divided by the total time taken is called its average speed.
![]()
Question 5.
Define acceleration.
Answer:
It is defined as the rate of change of velocity with time.
Acceleration = \(\frac{Change in velocity}{Time Taken}\)
or a = \(\frac{v-\mathbf{u}}{t}\)
The SI unit of acceleration is m/s2.
Question 6.
Draw a distance – time graph that represents uniform speed.
Answer:
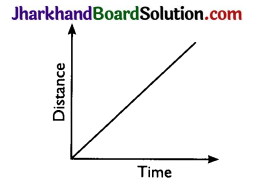
Question 7.
With the help of a distance – time graph show that the object is stationary.
Answer:
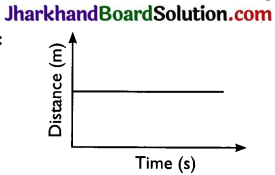
Question 8.
Define uniform circular motion.
Answer:
When a body moves in a circular path with uniform speed, its motion is called uniform circular motion.
Question 9.
Define scalar quantities. Give examples.
Answer:
The physical quantities which require only magnitude, and not the direction, for their complete description are called ‘scalars’ or ‘scalar quantities’. Distance, speed, time, area, etc., are all scalar quantities.
Question 10.
Define vector quantities. Give examples.
Answer:
The physical quantities which need both magnitude and direction for their complete description are called ‘vectors’ or vector quantities. Displacement, velocity, force, etc., are all vector quantities.
Question 11.
What is the SI unit of displacement?
Answer:
Metre (m).
Question 12.
A particle moves over three – quarters of a circle of radius. What is the magnitude of its displacement?
Answer:
When the particle covers three quarters of a circle, the magnitude of its displacement is
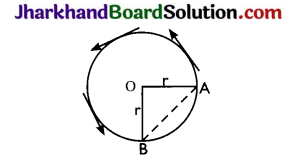
AB = \(\sqrt{\mathrm{OA}^{2}+\mathrm{OB}^{2}}\) = \(\sqrt{r^{2}+r^{2}}\)
= \(\sqrt{2 r}\) = √2 r
Question 13.
Can the average speed of a moving body ever be zero?
Answer:
Speed is a scalar quantity and is always positive. So the average speed of a moving body can never be zero.
Question 14.
What is the relationship between the distance travelled and the time elapsed for motion with uniform velocity?
Answer:
Distance is directly proportional to the time elapsed. In fact,
Distance travelled = Uniform velocity × Time elapsed
Question 15.
What is the SI unit of acceleration?
Answer:
The SI unit of acceleration is m/s2.
Question 16.
What is acceleration of a body moving with uniform velocity?
Answer:
The acceleration of a body moving with uniform velocity is zero.
Question 17.
State a relationship connecting u, v, a and t for an accelerated motion. Give an example of motion in which acceleration is uniform.
Answer:
The relationship between u, v, a and t is v = u + at A body falling freely towards the earth has a uniform acceleration of 9.8 ms-2.
Question 18.
Express the velocity of a body in uniform circular motion in terms of its time period T.
Answer:
Suppose a body of mass m rotates in a circle of radiusr with velocity v. It completes one revolution in time T. Then,
Velocity = \(\frac{Distance}{Time}\)[/latex] = \(\frac{Circumference}{Time period }\)[/latex]
or v = \(\frac{2 \pi \mathrm{r}}{\mathrm{T}}\)
Analysing & Evaluating Questions
Question 19.
The cars A, B, C and D are moving on a levelled road. Their distance versus time graphs are shown in the figure. Which car is the slowest?
Answer:
Speed = Slope of distance – time graph. The smaller the slope, the smaller is the speed
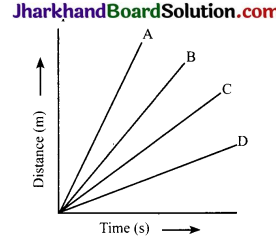
From the given figure, slope is minimum for car D. So, D is the slowest car.
Question 20.
A rubber ball dropped from a certain height bounce to certain height. This height keeps decreasing in subsequent bounces. What type of motion does the ball exhibit?
Answer:
The ball exhibits non – uniform motion.
![]()
Question 21.
A vehicle is moving at a constant velocity of 10 km/h in the north – south direction. It turns and starts moving towards east. What is the velocity of the vehicle towards east before taking the turn?
Answer:
Zero. The component of velocity at right angle to the original direction of motion is zero.
Short Answer Type Questions
Question 1.
Define the term rest and motion.
Answer:
- Rest: If a body does not change its position with respect to its surroundings, the body is said to be at rest, e.g., a table lying in a room is at rest with respect to the walls of the room.
- Motion: A body is said to be in motion if it changes its position with respect to its surroundings, e.g., a car running on the road is in motion with respect to the lamp posts, trees or bus stop on the roadside.
Question 2.
What is meant by a point object? Give some examples.
Answer:
Whenever the size of the object is much smaller than the distance it moves in a given time interval, the size of the object can be neglected. The object can be regarded as a point object in such cases.
Examples:
- A car covering a distance of 10km can be treated as a point object.
- Earth can be regarded as a point object for studying its motion around the sun.
Question 3.
Give some examples of straight line motion.
Answer:
Examples:
- A bus moving on a straight road
- A train moving on a straight track
- A runner running along a straight track
- A ball moving along a straight path
- An object falling vertically downwards towards the surface of the earth.
Question 4.
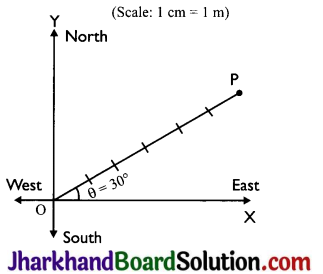
How can we specify the position of an object?
Answer:
1. The position of an object can be specified by choosing:
- a fixed point called ‘origin’ or reference point, and
- a fixed line passing through the origin, called reference axis.
2. So the position of an object can be fully described by knowing:
- its distance from origin O and
- the angle 0 which the line joining the origin ‘O’ and the object makes with the reference axis.
In the figure shown below, the position of an object located at point P is 6 cm from the origin and 30° north of east. v (Scale: 1cm = 1m)
Question 5.
A body moves in a circle of radius ‘2R’. What is the distance covered and displacement of the body after 2 complete rounds?
Answer:
Distance covered after 2 complete rounds = 2 × circumference
= 2 × 2π (2R) = 8πR
Displacement = zero, because initial and final positions of the body are the same and displacement is the shortest distance between initial and final positions.
Question 6.
Define the term velocity. What is its SI unit? Is it a scalar or a vector quantity?
Answer:
Velocity is a physical quantity that gives both speed and direction of motion of the body.
Definition: Velocity of a body is defined as the displacement produced per unit time. Velocity is also defined as the speed of a body in a givendirection. If ‘s’ is the distance travelled by a body in a given direction and ‘t’ is the time taken to travel that distance, then the velocity V is given by,
Velocity = \(\frac{Displacement}{Time}\)[/latex]
SI unit of velocity is m/s. Velocity is a vector quantity because it requires both magnitude and direction of a body.
Question 7.
Give the difference between distance and displacement.
| Distance | Displacement |
| (a) It is the total path covered by an object. | (a) It is the shortest path from initial position to the final position. |
| (b) It does not have any direction. | (b) It has direction. |
| (c) It cannot be zero.V | (c) It can be positive, negative or zero. |
Question 8.
Differentiate between speed and velocity.
Answer:
| Speed | Velocity |
| (a) It is the distance travelled by an object per unit of time. | (a) It is the displacement of the body per unit time. |
| (b) It is a scalar quantity, direction not required. | (b) It is a vector quantity, direction is required. |
| (c) It is always positive. | (c) It can be positive, negative or zero. |
Question 9.
A cheetah is the fastest land animal and can achieve a peak velocity of 100 km/h upto distances less than 500 m. If a cheetah spots his prey at a distance of 100 m, what is the minimum time it will take to get its prey, if the average velocity attained by it is 90 km/h?
Answer:
Here v = 90Km/h = \(\frac{90 \times 1000 \mathrm{~m}}{3600 \mathrm{~s}}\)
= 25m/s
s = 100m
Minimum time, t = \(\frac{s}{v}\) = \(\frac{100}{25}\) = 4s
Question 10.
The Rajdhani Express travels a distance of 1384 km from Mumbai to Delhi. It starts from Mumbai at 4.00 p.m. and reaches Delhi at 9.00 a.m. the next day. What is its average speed?
Answer:
Total distance travelled = 1384 km
Total time taken = 17 hours
Average speed =\(\frac{Total distance travelled}{Total time taken}\)= \(\frac{1384}{17}\)
= 81.4 km/h
Question 11.
A body starts initially with a velocity ‘u’ and is accelerated at constant rate ‘a’. Find an expression for final velocity after time ‘t’
Answer:
First equation of motion : Let a body start with initial velocity ‘u’ and after time ‘t’, its velocity becomes ‘v’ due to uniform acceleration ‘a’. From the definition of acceleration,
Acceleration = \(\frac{Change in velocity }{Time taken}\)
= \(\frac{Final velocity – Initial velocity}{Time taken}\)
a = \(=\frac{\mathrm{V}-\mathrm{u}}{\mathrm{t}}\)
at = v – u
v = u + at.
Question 12.
Deduce the expression for the distance travelled by a body moving with uniform acceleration in a given time.
Answer:
Second equation of motion:
Suppose a body starts with initial velocity ‘u’ and due to uniform acceleration ‘a’ its final velocity becomes ‘v’ after time ‘t’ Then,
Average velocity = \(\frac{Initial velocity + Final velocity}{2}\)
=\(\frac{u+v}{2}\)
So, the distance covered by the body in time t is
s = Average velocity × Time =\(\frac{u+v}{2}\) × t = \(\frac{\mathrm{u}+(\mathrm{u}+\mathrm{at}) \times \mathrm{t}}{2}\)
= \(\frac{2 u t + a t^{2}}{2}\)
or s = ut + \(\frac{1}{2}\) at 2
![]()
Question 13.
Establish the relation v2 – u2 = 2as, where ‘u’ is the initial velocity, ‘v’ is the final velocity, ‘a’ is the uniform acceleration and ‘s’ is the distance covered by the body.
Answer:
Third equation of motion:
Let a body start with initial velocity ‘u’ and after covering distance ‘s’ under uniform acceleration ‘a’, its velocity becomes ‘v’ in ‘t’ seconds. Then
Average velocity = \(\frac{\mathrm{u}+\mathrm{v}}{2 \mathrm{}}\)
So the distance covered in time t is given by
s = Average velocity x Time
= \(\frac{u+v}{2}\) × t
or v + u = \(\frac{2 s}{t}\) …………..(1)
Using the first equation of motion: v = u + at
or v – u = at … (ii)
Multiplying equations (i) and (ii), we get
(v + u) (v – u) = \(2 \frac{s}{t}\) × at
or v2 – u2 = 2as
Question 14.
Show that the slope of distance – time graph gives velocity of the body.
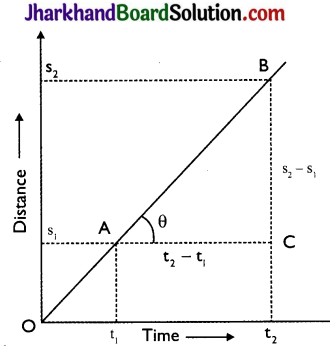
Answer:
Given figure shows distance – time graph for a body moving with uniform velocity. Clearly, it covers distances s1 and s2 in times t1 and t2 respectively.
Slope of line AB = tan θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
= \(\frac{s_{2}-s_{1}}{t_{2}-t_{1}}\) = \(\frac{Displacement}{Time}\) = velocity
Hence, the slope of the distance-time graph gives velocity of the body.
Question 15.
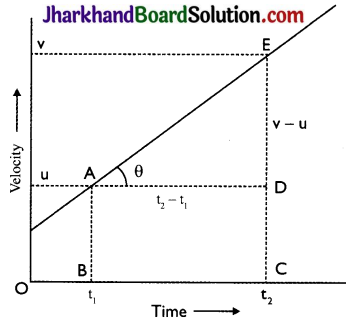
Show that the slope of velocity time graph gives acceleration of the body.
Answer:
Given figure shows the velocity – time graph for a body in uniform acceleration. It is a straight line inclined to the time – axis. Body has velocities ‘u’ and ‘v’ at times ‘t1’ and ‘t2’ respectively
Img-1
Slope of line AE = tan θ = \( \frac{E D}{A D}\)
\(\frac{v-u}{t_{2}-t_{1}}\) = \( \frac{Change in velocity}{Time taken}\)
= Acceleration of the body
Hence, the slope of the velocity – time graph gives the acceleration of the body.
Question 16.
Draw velocity – time graph for a body moving with uniform velocity. Hence show that the area under the velocity time graph gives the distance travelled by the body in a given time interval.
Answer:
In the given figure, line PQ is the velocity – time graph of a body moving with a uniform velocity such that OP = v Area of rectangle ABCD = AD × AB
= OP × AB
= v × (t2 – t1)
= Velocity × Time
= Distance travelled in time interval (t2 – t1)
Hence, the area under the velocity – time graph gives the distance travelled by the body in the given time interval.
Question 17.
The odometer of a car reads 1800 km at the start of a trip and 2400 km at the end of the trip. If the trip took 10h, calculate the average speed of the car in km/h and m/s.
Answer:
Distance covered by the car (s)
= 2400 – 1800 = 600 km.
Trip time = 10h
Average speed = ?
(i) Vav = \(\frac{s}{t}\) = \(\frac{600}{10}\) km = 60 km/h
(ii) In m/s : (60 km/h) = \(\frac{60 \times 1000}{60 \times 60}\)
= 16.7 m/s
The average speed of the car in km/h is 60 km/h and in m/s is 16.7 m/s.
Question 18.
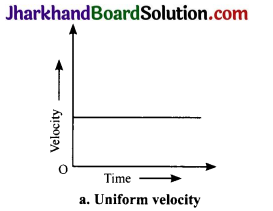
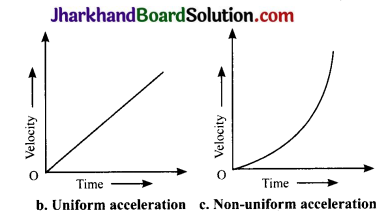
Draw velocity – time graphs to show the following:
(a) Uniform velocity
(b) Uniform acceleration
(c) Non – uniform acceleration
Answer:
Analysing & Evaluating Questions
Question 19.
The table given below shows distance (in km) travelled by bodies A, B and C. Read the data carefully and answer the following questions.
| Distance (in km) covered by different bodies | |||
| Time (s) | Body(A) | Body (B) | Body (C) |
| 1st second | 20 | 20 | 20 |
| 2nd second | 20 | 36 | 60 |
| 3rd second | 20 | 24 | 100 |
| 4th second | 20 | 30 | 140 |
| 5 th second | 20 | 48 | 180 |
(a) Which of the bodies is moving with
(i) constant speed?
(ii) constant acceleration?
(b) Which of the bodies covers
(i) maximum distance in 3rd second?
(ii) minimum distance in 3rd second?
Answer:
(a) (i) Body A
(ii) Body C
(b) (i) Body C
(ii) Body A
Question 20.
An electron moving with a velocity of 5 × 104ms-1 enters a uniform electric field and acquires a uniform acceleration of 104ms-2 in the direction of its initial motion.
(a) Calculate the time in which the electron would acquire a velocity double of its initial velocity.
(b) How much distance the electron would cover in this time?
Answer:
(i) Acceleration = \(\frac{ Change in velocity}{Time taken}\)
or Time taken, t = \(\frac{5 \times 10^{4} \mathrm{~m} \mathrm{~s}^{-1}}{10^{4} \mathrm{~m} \mathrm{~s}^{-2}}\)
= 5 s
(ii) s = ut + \(\frac{1}{2}\) at2
= (5 × 104 m s-1 × 5 s) + \(\frac{1}{2}\) × 104m s-2 × (5s)2
= 37.5 × 104 m
Long Answer Type Questions
Question 1.
Describe the various types of motion observed in bodies.
Answer:
Various types of motion as observed in bodies are:
- Translatory motion: When a body moves, as a whole, along a straight or curved path, it is said to be in translatory motion. Translatory motion is again of two types:
- Rectilinear motion : Here a body moves as a whole along a straight path. For example, a train moving on a straight track has translatory rectilinear motion.
- Curvilinear motion : In this case a body moves as a whole along a curved path. For example, motion of a bicycle taking a turn along a curved path.
- Rotatory motion: When a body rotates about a fixed point or axis. it exhibits a rotatory motion. For example, motion of a flywheel about a shaft
- Vibratory or oscillatory motion: When a body moves to and fro about a mean position, the motion is said to be vibratory or oscillatory motion. For example, the motion of the pendulum of a wall – clock.
- Complex motion: When the motion of a body may be a combination of more than one type of motion, it is said to be a complex motion. For example, a ball rolling down an inclined plane has both translatory and rotatory motions.
Question 2.
Define average velocity when the velocity of a body changes at a non – uniform rate and a uniform rate.
Answer:
Average velocity : When the velocity of a body changes at a non – uniform rate, its average velocity is defined as the net displacement covered divided by the total time taken.
Average velocity = \(\frac{Net displacement}{Total time taken}\)
When the velocity of a body changes at a uniform rate, the average velocity is given by the arithmetic mean of initial velocity and final velocity for a given period of time.
Average velocity = \(\frac{Initial velocity + Final velocity}{2}\) :
If u is the initial velocity and v is the final velocity, the average velocity vay is given by,
vay = \(=\frac{u+v}{2}\)
Question 3.
Explain the difference regarding the nature of acceleration of the three moving bodies as expressed by the following velocity – time graphs:
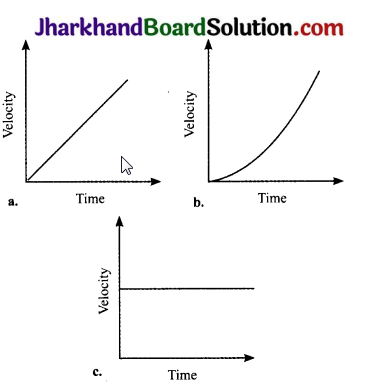
(a) Uniform acceleration: A body increases velocity by equal amounts in equal intervals of time.
(b) Non – uniform acceleration: A body travels unequal distances in equal intervals of time.
(c) Uniform motion or zero acceleration: A body moves with constant
Analysing & Evaluating Questions
Question 4.
Two stones are thrown vertically upwards simultaneously with their initial velocities u1 and u2 respectively. Prove that the heights reached by them would be in the ratio of \(\mathbf{u}_{1}^{2}\) : \(\mathbf{u}_{2}^{2}\) (Assume upward acceleration is – g and downward acceleration to be + g).
Answer:
Stone 1
Initial velocity = u1
Acceleration = – g
Height = h,
Final velocity, v = 0
Using the equation, v2 – u2 =2as
0 – \(\vec{a}\) = 2 (- g) × h1
h1 = \(\frac{-u_{1}^{2}}{-2 g}\) = \(\frac{u_{1}^{2}}{2 g}\) ……..(1)
Stone 2
Initial velocity = u1
Acceleration = – g
Height = h2
Final velocity, v = 0
02 \(-u_{2}^{2}\) = 2 (- g) × h2
h2 = \(\frac{-u_{2}^{2}}{-2 g}\) =\(\frac{u_{2}^{2}}{2 g}\) ……..(ii)
This gives; h1 : h2 = \(\vec{a}\) : \(\vec{a}\)
= \(=\frac{u_{1}^{2}}{2 g}\) : \(\frac{\mathrm{u}_{2}^{2}}{2 \mathrm{~g}}\)
=\(u_{1}^{2}\) : \(\vec{a}\)
Activity 1
- In your everyday life, you come across a range of motions in which:
- acceleration is in the direction of motion
- acceleration is against the direction of motion
- acceleration is uniform
- acceleration is non – uniform
- Observe these motions carefully and identify one example each of the above type of motions.
Observations
- A car moving on a road.
- A ball thrown up.
- Fan blades rotating
- Windmill at time moves fast when the wind speed is more and becomes slow when the wind speed decreases.
Activity 2
- Take piece of thread and tie a small piece of stone at one of its end. Move the stone to describe a circular path with constant speed by holding the thread at the other end.
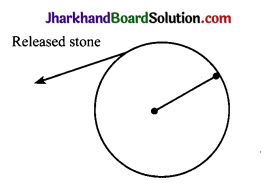
- Now, let the stone go by releasing the thread.
- Observe the direction in which the stone moves after it is released.
- By repeating the activity for a few more times and releasing the stone at different positions of the circular path, carefully observe whether the direction in which the stone moves remains the same or not.
Observations
- When the stone is released, it moves along a straight line, tangential to the circular path.
- By repeating the activity and releasing the stone at different positions of the circular path, the direction in which the stone moves does not remain the same. It changes every time.
Value Based Questions
Question 1.
The speed limits are prescribed for vehicles running on highways. Why is it essential to follow the speed limit rules?
Answer:
Speed limits are prescribed on the highways/expressways because:
1. When a vehicle is made to run at height speeds, its tyres get hot (due to friction). This makes them softer and the air inside the tubes hotter Both. these factors may lead to bursting of tyre/tube.
2. Reflex time varies from person to person. Any running vehicle needs a certain time period to stop after the brakes are applied. At higher speeds, this time period becomes shorter.
3. As a result, the chances of collision increase. Because of these reasons, one should strictly follow the speed limit regulations. Also, it is safer to drive in your lane depending upon the speed of your vehicle.
4. Moral: Drive below the speed limit and in your lane.
Question 2.
Most drivers involved in road accidents are found to be drunk. Give reason.
Answer:
The reflex time of a person increases when drunk, (average reflex time of a normal person is about 1/15s). Therefore, such a driver of vehicle will take more time in applying brakes. As a result, the vehicle may not stop well in time and cause an accident.