Bhagya

JAC Jharkhand Board Class 9th Maths Important Questions in Hindi & English Medium

JAC Board Class 9th Maths Important Questions in English Medium

• Chapter 1 Number Systems Important Questions
• Chapter 2 Polynomials Important Questions
• Chapter 3 Coordinate Geometry Important Questions
• Chapter 4 Linear Equations in Two Variables Important Questions
• Chapter 5 Introduction to Euclid’s Geometry Important Questions
• Chapter 6 Lines and Angles Important Questions
• Chapter 7 Triangles Important Questions
• Chapter 8 Quadrilaterals Important Questions
• Chapter 9 Areas of Parallelograms and Triangles Important Questions
• Chapter 10 Circles Important Questions
• Chapter 11 Constructions Important Questions
• Chapter 12 Heron’s Formula Important Questions
• Chapter 13 Surface Areas and Volumes Important Questions
• Chapter 14 Statistics Important Questions
• Chapter 15 Probability Important Questions

JAC Board Class 9th Maths Important Questions in Hindi Medium

• Chapter 1 संख्या पद्धति Important Questions
• Chapter 2 बहुपद Important Questions
• Chapter 3 निर्देशांक ज्यामिति Important Questions
• Chapter 4 दो चरों वाले रैखिक समीकरण Important Questions
• Chapter 5 युक्लिड के ज्यामिति का परिचय Important Questions
• Chapter 6 रेखाएँ और कोण Important Questions
• Chapter 7 त्रिभुज Important Questions
• Chapter 8 चतुर्भुज Important Questions
• Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Important Questions
• Chapter 10 वृत्त Important Questions
• Chapter 11 रचनाएँ Important Questions
• Chapter 12 हीरोन का सूत्र Important Questions
• Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Important Questions
• Chapter 14 सांख्यिकी Important Questions
• Chapter 15 प्रायिकता Important Questions

Jharkhand Board JAC Class 10 Maths Solutions Chapter 12 Areas Related to Circles Ex 12.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 12 Areas Related to Circles Exercise 12.3

Unless stated otherwise, use π = \(\frac{22}{7}\)

Question 1.
Find the area of the shaded region in the figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.

Solution:
Given, PQ = 24 cm, PR = 7 cm.
We know any triangle drawn from diameter RQ to the circle is 90°.
Here, ∠RPQ = 90°
In right ΔRPQ, RQ² = PR² + PQ² (By Pythagoras theorem)
RQ² = 7² + 24²
RQ² = 49 + 576
RQ² = 625
RQ = 25 cm
∴ Area of ΔRPQ = \(\frac{1}{2}\) × RP × PQ
= \(\frac{1}{2}\) × 7 × 24 = 84 cm²
∴ Area of semi-circle = \(\frac{\pi r^2}{2}=\frac{22}{7 \times 2}\left(\frac{25}{2}\right)^2\) (∵ r = \(\frac{\mathrm{PQ}}{2}=\frac{25}{2}\) cm)
= \(\frac{11 \times 625}{28}=\frac{6875}{28} \mathrm{~cm}^2\)
∴ Area of the shaded region = Area of the semi-circle – Area of right ΔRPQ
= \(\frac{6875}{28}-84\)
= \(\frac{6875-2352}{28}=\frac{4523}{28}\) cm².

Question 2.
Find the area of the shaded region in the figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.

Solution:
R – radius of the bigger circle, r – radius of the smaller circle.
Area of the shaded portion = Area of sector OAC – Area of sector OBD

Question 3.
Find the area of the shaded region in the figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.

Solution:
Area of the shaded portion = Area of the square – 2 × Area of one semicircle
= (14 × 14) – 2 × \(\frac{\pi r^2}{2}\) [∵ r = 7]
= 14 × 14 – 2 × \(\frac{22}{7} \times \frac{7 \times 7}{2}\)
= 196 – 154 = 42 cm².

Question 4.
Find the area of the shaded region in the figure, where a circular are of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.

Solution:
Area of the shaded portion = Area of the circle of radius 6 cm + Area of equilateral ΔABC – Area of the sector

Question 5.
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the figure. Find the area of the remaining portion of the square.

Solution:
Area of the shaded portion = Area of the square – Area of the 4 quadrants – Area of the circle
= (4 × 4) – 4 × area of one quadrant – area of the circle

Question 6.
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the figure. Find the area of the design.

Solution:
Area of the design (shaded region) = Area of the circle – Area of ΔABC
Area of equilateral triangle ABC = \(\frac{\sqrt{3} a^2}{4}\)
In ΔABC, AL ⊥ BC.

Alternative Method:

Area of shaded region
= 3[Area of segments]
= 3[Area of sector – Area of ΔOBC]
= 3[\(\pi r^2 \frac{\theta}{360^{\circ}}-\frac{1}{2}\) × BC × OL]

Question 7.
In the figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region.

Solution:
Area of the shaded region = Area of the square – Area of the 4 quadrants
= Area of the square – 4 × area of one quadrant
= (14)² – 4 × \(\frac{1}{4}\)πr²
= (14)² – 4 × \(\frac{1}{4} \times \frac{22}{7}\) × 7 × 7
= 196 – 154
= 42 cm².

Question 8.
The figure depicts a racing track whose left and right ends are semicircular.
The distance between the two inner parallel line segments is 60 m and they are each 106 m. long. If the track is 10 m wide, find:
(i) the distance around the track along its inner edge.
(ii) the area of the track.

Solution:
i) Distance around the inner track

ii) Area of the track:

Area of the track = l × b + l × b + 2\(\left[\frac{\pi \mathrm{R}^2}{2}-\frac{\pi \mathrm{r}^2}{2}\right]\) r = 30 mts, R = (30 + 10) = 40 mts.
= 106 × 10 + 106 × 10 + 2 × \(\frac{\pi}{2}\)(R² – r²)
= 1060 + 1060 + \(\frac{22}{7}\)[40² – 30²]
= 2120 + \(\frac{22}{7}\)[1600 – 900]
= 2120 + \(\frac{22}{7}\)[700]
= 2120 + 2200
= 4320 m².

Question 9.
In the figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.

Solution:
Given,
OA = 7 cm
∴ OD = 7 cm
Now, area of smaller circle whose diameter (OD) = 7 cm is

Now,
Area of ΔABC = \(\frac{1}{2}\) × AB × OC
= \(\frac{1}{2}\) × 2 × OA × OC
= \(\frac{1}{2}\) × 14 × 7 (∵ OA = OC)
= 49 cm².
Area of semi-circle ABCA = \(\frac{\pi r^2}{2}=\frac{22}{7 \times 2}(7)^2\)
= 77 cm²
∴ Area of segments BC and AC = Area of semi-circle – Area of AABC
= 77 – 49 = 28 cm²
∴ Area of total shaded region = Area of small circle + Area of segments BC and AC
= \(\frac{77}{2}\) + 28
= 38.5 + 28
= 66.5 cm².

Question 10.
The area of an equilateral triangle ABC is 17320.5 cm². With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle. Find the area of the shaded region. (Use π = 3.14 and \(\sqrt{3}\) = 1.73205).

Solution:
Area of the shaded portion = Area of equilateral ΔABC – Area of sector Axy – Area of sector Bxz – Area of sector Cyz.
π = 3.14, θ = 60°, r = ?, r = \(\frac{a}{2}\)
Area of the shaded portion = Area of the equilateral Δ – 3 × Area of one sector

Area of the shaded region = Area of ΔABC – \(\frac{3 \times \pi r^2 \theta}{360}\)
= 17320.5 – \(\frac{3 \times 3.14 \times 100 \times 100 \times 60}{360}\)
= 17320.5 – 1.57 × 10000
= 17320.5 – 15700.0
= 1620.5 sq.cm.

Question 11.
On a square handkerchief, nine circular designs each of radius 7 cm are made. Find the area of the remaining portion of the handkerchief.

Solution:
Number of circular designs = 9
Radius of the circular design = 7 cm
There are three circles in one side of the square handkerchief.
∴ Side of the square = 3 × diameter of circle = 3 × 14 = 42 cm
Area of the square = 42 × 42 cm² = 1764 cm²
Area of the circle = πr² = \(\frac{22}{7}\) × 7 × 7 = 154 cm²
Total area of the design = 9 × 154 = 1386 cm²
Area of the remaining portion of the handkerchief = Area of the square – Total area of the design
= 1764 – 1386
= 378 cm².

Question 12.
In the figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm find the area of the (i) quadrant OACB, (ii) shaded region.

Solution:

Question 13.
In the figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)

Solution:
Radius of the quadrant = Diagonal of the square (OB)
OB² = OA² + AB²
= 20² + 20²
= 400 + 400
= 800
OB2 = 400 × 2
OB = \(\sqrt{400 \times 2}\) = 20\(\sqrt{2}\)
Area of the shaded region = Area of the quadrant OPBQ – Area of the square OABC
= \(\frac{1}{4}\) πr² – (OA)²
= \(\frac{1}{4}\) × 3.14 × 20\(\sqrt{2}\) × 20\(\sqrt{2}\) – (20)²
= \(\frac{1}{4}\) × 3.14 × 400 × \(\sqrt{4}\) – 400
= \(\frac{1}{4}\) × 3.14 × 400 × 2 – 400
= 100 × 2 × 3.14 – 400
= 100 × 2(3.14 – 2)
= 200 × 1.14
= 228 sq.cm.

Question 14.
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O. If ∠AOB = 30°, find the area of the shaded region.

Solution:
R = 21, r = 7, θ = 30°, π = \(\frac{22}{7}\)
Area of the shaded region = Area of sector OAB – Area of sector OCD

Question 15.
In the figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

Solution:
BC² = 14² + 14²
BC² = 196 + 196 = 392
BC = \(\sqrt{392}\) = \(\sqrt{196 \times 2}\) = 14\(\sqrt{2}\) = d
r = \(\frac{14 \sqrt{2}}{2}=7 \sqrt{2}\)
Radius of the sector = 14.
Area of the shaded region Area of the semicircle BEC – Area of the segment BDCB

Question 16.
Calculate the area of the designed region in the figure common between the two quadrants of circles of radius 8 cm each.

Solution:
Area of the design = Area of sector DXB + Area of ΔDCB
Area of the segment DXB = Area of the sector DXBC – Area of ΔDCB

JAC Jharkhand Board Class 12th Maths Solutions in Hindi & English Medium

JAC Board Class 12th Maths Solutions in English Medium

JAC Class 12 Maths Chapter 1 Relations and Functions

• Chapter 1 Relations and Functions Ex 1.1
• Chapter 1 Relations and Functions Ex 1.2
• Chapter 1 Relations and Functions Ex 1.3
• Chapter 1 Relations and Functions Ex 1.4
• Chapter 1 Relations and Functions Miscellaneous Exercise

JAC Class 12 Maths Chapter 2 Inverse Trigonometric Functions

• Chapter 2 Inverse Trigonometric Functions Ex 2.1
• Chapter 2 Inverse Trigonometric Functions Ex 2.2
• Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise

JAC Class 12 Maths Chapter 3 Matrices

• Chapter 3 Matrices Ex 3.1
• Chapter 3 Matrices Ex 3.2
• Chapter 3 Matrices Ex 3.3
• Chapter 3 Matrices Ex 3.4
• Chapter 3 Matrices Miscellaneous Exercise

JAC Class 12 Maths Chapter 4 Determinants

• Chapter 4 Determinants Ex 4.1
• Chapter 4 Determinants Ex 4.2
• Chapter 4 Determinants Ex 4.3
• Chapter 4 Determinants Ex 4.4
• Chapter 4 Determinants Ex 4.5
• Chapter 4 Determinants Ex 4.6
• Chapter 4 Determinants Miscellaneous Exercise

JAC Class 12 Maths Chapter 5 Continuity and Differentiability

• Chapter 5 Continuity and Differentiability Ex 5.1
• Chapter 5 Continuity and Differentiability Ex 5.2
• Chapter 5 Continuity and Differentiability Ex 5.3
• Chapter 5 Continuity and Differentiability Ex 5.4
• Chapter 5 Continuity and Differentiability Ex 5.5
• Chapter 5 Continuity and Differentiability Ex 5.6
• Chapter 5 Continuity and Differentiability Ex 5.7
• Chapter 5 Continuity and Differentiability Ex 5.8
• Chapter 5 Continuity and Differentiability Miscellaneous Exercise

JAC Class 12 Maths Chapter 6 Application of Derivatives

• Chapter 6 Application of Derivatives Ex 6.1
• Chapter 6 Application of Derivatives Ex 6.2
• Chapter 6 Application of Derivatives Ex 6.3
• Chapter 6 Application of Derivatives Ex 6.4
• Chapter 6 Application of Derivatives Ex 6.5
• Chapter 6 Application of Derivatives Miscellaneous Exercise

JAC Class 12 Maths Chapter 7 Integrals

• Chapter 7 Integrals Ex 7.1
• Chapter 7 Integrals Ex 7.2
• Chapter 7 Integrals Ex 7.3
• Chapter 7 Integrals Ex 7.4
• Chapter 7 Integrals Ex 7.5
• Chapter 7 Integrals Ex 7.6
• Chapter 7 Integrals Ex 7.7
• Chapter 7 Integrals Ex 7.8
• Chapter 7 Integrals Ex 7.9
• Chapter 7 Integrals Ex 7.10
• Chapter 7 Integrals Ex 7.11
• Chapter 7 Integrals Miscellaneous Exercise

JAC Class 12 Maths Chapter 8 Application of Integrals

• Chapter 8 Application of Integrals Ex 8.1
• Chapter 8 Application of Integrals Ex 8.2
• Chapter 8 Application of Integrals Miscellaneous Exercise

JAC Class 12 Maths Chapter 9 Differential Equations

• Chapter 9 Differential Equations Ex 9.1
• Chapter 9 Differential Equations Ex 9.2
• Chapter 9 Differential Equations Ex 9.3
• Chapter 9 Differential Equations Ex 9.4
• Chapter 9 Differential Equations Ex 9.5
• Chapter 9 Differential Equations Ex 9.6
• Chapter 9 Differential Equations Miscellaneous Exercise

JAC Class 12 Maths Chapter 10 Vector Algebra

• Chapter 10 Vector Algebra Ex 10.1
• Chapter 10 Vector Algebra Ex 10.2
• Chapter 10 Vector Algebra Ex 10.3
• Chapter 10 Vector Algebra Ex 10.4
• Chapter 10 Vector Algebra Miscellaneous Exercise

JAC Class 12 Maths Chapter 11 Three Dimensional Geometry

• Chapter 11 Three Dimensional Geometry Ex 11.1
• Chapter 11 Three Dimensional Geometry Ex 11.2
• Chapter 11 Three Dimensional Geometry Ex 11.3
• Chapter 11 Three Dimensional Geometry Miscellaneous Exercise

JAC Class 12 Maths Chapter 12 Linear Programming

• Chapter 12 Linear Programming Ex 12.1
• Chapter 12 Linear Programming Ex 12.2
• Chapter 12 Linear Programming Miscellaneous Exercise

JAC Class 12 Maths Chapter 13 Probability

• Chapter 13 Probability Ex 13.1
• Chapter 13 Probability Ex 13.2
• Chapter 13 Probability Ex 13.3
• Chapter 13 Probability Ex 13.4
• Chapter 13 Probability Ex 13.5
• Chapter 13 Probability Miscellaneous Exercise

JAC Board Class 12th Maths Solutions in Hindi Medium

JAC Class 12 Maths Chapter 1 संबंध एवं फलन

• Chapter 1 संबंध एवं फलन Ex 1.1
• Chapter 1 संबंध एवं फलन Ex 1.2
• Chapter 1 संबंध एवं फलन Ex 1.3
• Chapter 1 संबंध एवं फलन Ex 1.4
• Chapter 1 संबंध एवं फलन विविध प्रश्नावली

JAC Class 12 Maths Chapter 2 प्रतिलोम त्रिकोणमितीय फलन

• Chapter 2 प्रतिलोम त्रिकोणमितीय फलन Ex 2.1
• Chapter 2 प्रतिलोम त्रिकोणमितीय फलन Ex 2.2
• Chapter 2 प्रतिलोम त्रिकोणमितीय फलन विविध प्रश्नावली

JAC Class 12 Maths Chapter 3 आव्यूह

• Chapter 3 आव्यूह Ex 3.1
• Chapter 3 आव्यूह Ex 3.2
• Chapter 3 आव्यूह Ex 3.3
• Chapter 3 आव्यूह Ex 3.4
• Chapter 3 आव्यूह विविध प्रश्नावली

JAC Class 12 Maths Chapter 4 सारणिक

• Chapter 4 सारणिक Ex 4.1
• Chapter 4 सारणिक Ex 4.2
• Chapter 4 सारणिक Ex 4.3
• Chapter 4 सारणिक Ex 4.4
• Chapter 4 सारणिक Ex 4.5
• Chapter 4 सारणिक Ex 4.6
• Chapter 4 सारणिक विविध प्रश्नावली

JAC Class 12 Maths Chapter 5 सांतत्य तथा अवकलनीयता

• Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.1
• Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.2
• Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.3
• Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.4
• Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.5
• Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.6
• Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.7
• Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.8
• Chapter 5 सांतत्य तथा अवकलनीयता विविध प्रश्नावली

JAC Class 12 Maths Chapter 6 अवकलज के अनुप्रयोग

• Chapter 6 अवकलज के अनुप्रयोग Ex 6.1
• Chapter 6 अवकलज के अनुप्रयोग Ex 6.2
• Chapter 6 अवकलज के अनुप्रयोग Ex 6.3
• Chapter 6 अवकलज के अनुप्रयोग Ex 6.4
• Chapter 6 अवकलज के अनुप्रयोग Ex 6.5
• Chapter 6 अवकलज के अनुप्रयोग विविध प्रश्नावली

JAC Class 12 Maths Chapter 7 समाकलन

• Chapter 7 समाकलन Ex 7.1
• Chapter 7 समाकलन Ex 7.2
• Chapter 7 समाकलन Ex 7.3
• Chapter 7 समाकलन Ex 7.4
• Chapter 7 समाकलन Ex 7.5
• Chapter 7 समाकलन Ex 7.6
• Chapter 7 समाकलन Ex 7.7
• Chapter 7 समाकलन Ex 7.8
• Chapter 7 समाकलन Ex 7.9
• Chapter 7 समाकलन Ex 7.10
• Chapter 7 समाकलन Ex 7.11
• Chapter 7 समाकलन विविध प्रश्नावली

JAC Class 12 Maths Chapter 8 समाकलनों के अनुप्रयोग

• Chapter 8 समाकलनों के अनुप्रयोग Ex 8.1
• Chapter 8 समाकलनों के अनुप्रयोग Ex 8.2
• Chapter 8 समाकलनों के अनुप्रयोग विविध प्रश्नावली

JAC Class 12 Maths Chapter 9 अवकल समीकरण

• Chapter 9 अवकल समीकरण Ex 9.1
• Chapter 9 अवकल समीकरण Ex 9.2
• Chapter 9 अवकल समीकरण Ex 9.3
• Chapter 9 अवकल समीकरण Ex 9.4
• Chapter 9 अवकल समीकरण Ex 9.5
• Chapter 9 अवकल समीकरण Ex 9.6
• Chapter 9 अवकल समीकरण विविध प्रश्नावली

JAC Class 12 Maths Chapter 10 सदिश बीजगणित

• Chapter 10 सदिश बीजगणित Ex 10.1
• Chapter 10 सदिश बीजगणित Ex 10.2
• Chapter 10 सदिश बीजगणित Ex 10.3
• Chapter 10 सदिश बीजगणित Ex 10.4
• Chapter 10 सदिश बीजगणित विविध प्रश्नावली

JAC Class 12 Maths Chapter 11 त्रि-विमीय ज्यामिति

• Chapter 11 त्रिविमीय ज्यामिति Ex 11.1
• Chapter 11 त्रिविमीय ज्यामिति Ex 11.2
• Chapter 11 त्रिविमीय ज्यामिति Ex 11.3
• Chapter 11 त्रिविमीय ज्यामिति विविध प्रश्नावली

JAC Class 12 Maths Chapter 12 रैखिक प्रोग्रामन

• Chapter 12 रैखिक प्रोग्रामन Ex 12.1
• Chapter 12 रैखिक प्रोग्रामन Ex 12.2
• Chapter 12 रैखिक प्रोग्रामन विविध प्रश्नावली

JAC Class 12 Maths Chapter 13 प्रायिकता

• Chapter 13 प्रायिकता Ex 13.1
• Chapter 13 प्रायिकता Ex 13.2
• Chapter 13 प्रायिकता Ex 13.3
• Chapter 13 प्रायिकता Ex 13.4
• Chapter 13 प्रायिकता Ex 13.5
• Chapter 13 प्रायिकता विविध प्रश्नावली

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 Quadratic Equations Ex 4.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 Quadratic Equations Exercise 4.3

Question 1.
Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
1. 2x² – 7x + 3 = 0
2. 2x² + x – 4 = 0
3. 4x² + 4\(\sqrt{3}\)x + 3 = 0
4. 2x² + x + 4 = 0
Solution:
1. 2x² – 7x + 3 = 0
Dividing throughout by 2, we get

Thus, the roots of the given quadratic equation are 3 and \(\frac{1}{2}\).

2. 2x² + x – 4 = 0
Dividing throughout by 2, we get

Thus, the roots of the given quadratic equation are \(\frac{-1+\sqrt{33}}{4}\) and \(\frac{-1-\sqrt{33}}{4}\)

3. 4x² + 4\(\sqrt{2}\)x + 3 = 0
4x² + 4\(\sqrt{3}\)x + (\(\sqrt{3}\))² = 0
(2x + \(\sqrt{3}\))² = 0
(2x + \(\sqrt{3}\)) (2x + \(\sqrt{3}\)) = 0
2x + \(\sqrt{3}\) = 0 or 2x + \(\sqrt{3}\) =0
x = \(-\frac{\sqrt{3}}{2}\) or x = \(-\frac{\sqrt{3}}{2}\)
Thus, the roots of the given quadratic equation are \(-\frac{\sqrt{3}}{2}\) and \(-\frac{\sqrt{3}}{2}\)

4. 2x² + x + 4 = 0
Dividing throughout by 2, we get

But, the square of any real number cannot be negative.
Hence, the real roots of the given quadratic equation do not exist.

Question 2.
Find the roots of the quadratic equations given in Q.1 by applying the quadratic formula.
1. 2x² – 7x + 3 = 0
Here, a = 2, b = -7 and c = 3.
Then, b² – 4ac = (-7)² – 4(2)(3) = 25
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ x = \(\frac{7 \pm \sqrt{25}}{2(2)}\)
∴ x = \(\frac{7 \pm 5}{4}\)
∴ x = 3 or x = \(\frac{1}{2}\)
Thus, the roots of the given quadratic equation are 3 and \(\frac{1}{2}\).

2. 2x² + x – 4 = 0
Here, a = 2, b = 1 and c = -4.
Then, b² – 4ac = (1)² – 4(2)(-4) = 33
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ x = \(\frac{-1 \pm \sqrt{33}}{2(2)}\)
∴ x = \(\frac{-1 \pm \sqrt{33}}{4}\)
Thus, the roots of the given quadratic equation are \(\frac{-1 \pm \sqrt{33}}{4}\) and \(\frac{-1-\sqrt{33}}{4}\)

3. 4x² + 4\(\sqrt{3}\)x + 3 = 0
Here, a = 4, b = 4\(\sqrt{3}\) and c = 3.
Then, b² – 4ac = (4\(\sqrt{3}\))² – 4(4)(3) = 0
Then, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ x = \(\frac{-4 \sqrt{3} \pm \sqrt{0}}{2(4)}\)
∴ x = \(-\frac{\sqrt{3}}{2}\) or x = \(-\frac{\sqrt{3}}{2}\)
Thus, the roots of the given quadratic equation are \(-\frac{\sqrt{3}}{2}\) and \(-\frac{\sqrt{3}}{2}\).

4. 2x² + x + 4 = 0
Here, a = 2, b = 1 and c = 4.
Then, b² – 4ac = (1)² – 4 (2)(4) = -31 < 0
Since b² – 4ac < 0 for the given quadratic equation, the real roots of the given quadratic equation do not exits.

Question 3.
Find the roots of the following equations:
1. x – \(\frac{1}{x}\) = 3, x ≠ 0
2. \(\frac{1}{x+4}-\frac{1}{x-7}=\frac{11}{30}\); x ≠ -4, 7
Solution:
1. x – \(\frac{1}{x}\) = 3, x ≠ 0
∴ x² – 1 = 3x
∴ x² – 3x – 1 = 0
Here, a = 1, b = -3 and c = -1.
Then, b² – 4ac = (-3)² – 4(1)(-1) = 13
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{3 \pm \sqrt{13}}{2(1)}\)
x = \(\frac{3 \pm \sqrt{13}}{2}\)
Thus, the roots of the given equation are \(\frac{3+\sqrt{13}}{2}\) and \(\frac{3-\sqrt{13}}{2}\).

2. \(\frac{1}{x+4}-\frac{1}{x-7}=\frac{11}{30}\); x ≠ -4, 7
∴ \(\frac{(x-7)-(x+4)}{(x+4)(x-7)}=\frac{11}{30}\)
∴ \(\frac{-11}{x^2-3 x-28}=\frac{11}{30}\)
∴ \(\frac{-1}{x^2-3 x-28}=\frac{1}{30}\)
∴ -30 = x² – 3x – 28
∴ x² – 3x + 2 = 0
Here, a = 1, b = -3 and c = 2.
Then, b² – 4ac = (-3)² – 4(1)(2) = 1
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ x = \(\frac{3 \pm \sqrt{1}}{2(1)}\)
∴ x = \(\frac{3 \pm 1}{2}\)
∴ x = 2 or x = 1
Thus, the roots of the given equation are 2 and 1.
Note: Here, the method of factorisation would turn out to be more easier.

Question 4.
The sum of the reciprocals of Rehman’s ages (in years), 3 years ago and 5 years from now is \(\frac{1}{3}\). Find his present age.
Solution:
Let the present age of Rehman be x years.
So, his age 3 years ago was (x – 3) years and his age 5 years hence will be (x + 5) years.
The sum of the reciprocals of these two ages (in years) is given to be \(\frac{1}{3}\).
∴ \(\frac{1}{x-3}+\frac{1}{x+5}=\frac{1}{3}\)
∴ \(\frac{x+5+x-3}{(x-3)(x+5)}=\frac{1}{3}\)
∴ 3(2x + 2) = (x – 3)(x + 5)
∴ 6x + 6 = x² + 2x – 15
∴ x² – 4x – 21 = 0
∴ x² – 7x + 3x – 21 = 0
∴ x(x – 7) + 3(x – 7) = 0
∴ (x – 7)(x + 3) = 0
∴ x – 7 = 0 or x + 3 = 0
∴ x = 7 or x = -3
Now, since x represents the present age of Rehman, it cannot be negative, i,e., x ≠ -3.
∴ x = 7
Thus, the present age of Rehman is 7 years.

Question 5.
In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of those marks would have been 210. Find her marks in the two subjects.
Solution:
Let Shefali’s marks in Mathematics be x.
Then, her marks in English = 30 – x, as her total marks in Mathematics and English is 30.
Had she scored 2 marks more in Mathematics and 3 marks less in English, her score in Mathematics would be x + 2 and in English would be 30 – x – 3 = 27 – x.
∴ (x + 2) (27 – x) = 210
∴ 27x – x² + 54 – 2x = 210
∴ -x² + 25x + 54 – 210 = 0
∴ -x² + 25x – 156 = 0
∴ x² – 25x + 156 = 0
∴ x² – 13x – 12x + 156 = 0
∴ x(x – 13) – 12(x – 13) = 0
∴ (x – 13)(x – 12) = 0
∴ x – 13 = 0 or x – 12 = 0
∴ x = 13 or x = 12
Then, 30 – x = 30 – 13 = 17 or
30 – x = 30 – 12 = 18
Thus, Shefall’s marks in Mathematics and in English are 13 and 17 respectively or 12 and 18 respectively.

Question 6.
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Solution:
Let the shorter side of the rectangular field be x m.
Then, it diagonal is (x + 60) m and the longer side is (x + 30) m.
In a rectangle, all the angles are right angles.
Hence, by Pythagoras theorem,
(Shorter side)² + (Longer side)² = (Diagonal)²
∴ x² + (x + 30)² = (x + 60)²
∴ x² + x² + 60x + 900 = x² + 120x + 3600
∴ x² – 60x – 2700 = 0
Here, a = 1, b = -60 and c = -2700.
Then, b² – 4ac = (-60)² – 4(1)(-2700)
= 3600 + 10800
= 14400
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{60 \pm \sqrt{14400}}{2(1)}\)
= \(\frac{60 \pm 120}{2}\)
∴ x = \(\frac{60+120}{2}\) or x = \(\frac{60-120}{2}\)
∴ x = 90 or x = -30
Since x denotes the shorter side of the rectangular field, x cannot be negative.
∴ x = 90
Then, x + 30 = 90 + 30 = 120
Thus, the shorter side (breadth) of the rectangular field is 90 m and the longer side (length) of the rectangular field is 120 m.

Question 7.
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
Solution:
Let the smaller number be x.
Then, the larger number = \(\frac{x^2}{8}\)
Now, the difference of their squares is 180.
∴ \(\left(\frac{x^2}{8}\right)^2-(x)^2=180\)
∴ \(\frac{x^4}{64}-x^2=180\)
∴ x⁴ – 64x² – 11520 = 0
Let x² = y
∴ x⁴ = y²
∴ y² – 64y – 11520 = 0
Here, a = 1, b = -64 and c = -11520.
Then, b² – 4ac = (-64)² – 4(1)(-11520)
= 4096 + 46080
= 50176
Now, y = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{64 \pm \sqrt{50176}}{2(1)}\)
= \(\frac{64 \pm 224}{2}\)
∴ y = \(\frac{64+224}{2}\) or y = \(\frac{64-224}{2}\)
∴ y = 144 or y = -80
∴ x² = 144 or x² = -80
But, x² = -80 is not possible.
∴ x² = 144
∴ x = 12 or x = -12
Then, \(\frac{x^2}{8}=\frac{144}{8}=18\)
Thus, the required numbers are 12 and 18 or -12 and 18.

Question 8.
A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution:
Let the usual uniform speed of the train be x km/h.
∴ Time taken to travel 360 km at the speed of x km/h = \(\frac{\text { distance }}{\text { speed }}\) = \(\frac{360}{x}\) hours.
If the speed had been 5 km/h more, the new speed would be (x + 5) km/h and the time taken to travel 360 km at this increased speed would be \(\frac{360}{x+5}\) hours.
Now, New time = Usual time – 1
∴ \(\frac{360}{x+5}=\frac{360}{x}-1\)
∴ 360x = 360x + 1800 – x(x + 5) (Multiplying by x(x + 5))
∴ 0 = 1800 – x² – 5x
∴ x² + 5x – 1800 = 0
∴ x² + 45x – 40x – 1800 = 0
∴ x(x + 45) – 40(x + 45) = 0
∴ (x + 45) (x – 40) = 0
∴ x + 45 = 0 or x – 40 = 0
∴ x = -45 or x = 40
As, x is the speed (in km/h) of the train, x = -45 is not possible.
∴ x = 40
Thus, the usual uniform speed of the train is 40 km/h.

Question 9.
Two water taps together can fill a tank in \(9 \frac{3}{8}\) hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution:
Let the time taken by the tap with smaller diameter to fill the tank be x hours.
Then, the time taken by the tap with larger diameter = (x – 10) hours.
So, the part of the tank filled in one hour by the tap with smaller diameter = \(\frac{1}{x}\) and by the tap with larger diameter = \(\left(\frac{1}{x-10}\right)\)
So, the part of tank filled in one hour by both the taps together = \(\frac{1}{x}+\frac{1}{x-10}\)
Both the taps together can fill the tank in \(9 \frac{3}{8}\) hours, i.e., \(\frac{75}{8}\) hours.
∴ The part of tank filled in one hour by both the tank together = \(\frac{8}{75}\)
∴ \(\frac{1}{x}+\frac{1}{x-10}=\frac{8}{75}\).
∴ 75(x – 10) + 75x = 8x (x – 10) (Multiplying by 75x(x – 10))
∴ 75x – 750 + 75x = 8x² – 80x
∴ 8x² – 230x + 750 = 0
Here, a = 8, b = -230 and c = 750.
∴ b² – 4ac = (-230)² – 4 (8)(750)
= 52900 – 24000
= 28900
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ x = \(\frac{230 \pm \sqrt{28900}}{2(8)}\)
∴ x = \(\frac{230 \pm 170}{16}\)
∴ x = \(\frac{400}{16}\) or x = \(\frac{60}{16}\)
∴ x = 25 or x = 3.75
But, x ≠ 3.75, because for x = 3.75, x – 10 < 0.
∴ x = 25 and x – 10 = 15
Thus, the time taken by the tap with smaller diameter is 25 hours and that by the tap. with larger diameter is 15 hours.

Question 10.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.
Solution:
Let the average speed of the passenger train be x km/h.
Then, the average speed of the express train is (x + 11) km/h.
∴ Time taken by passenger train to cover 132 km = \(\frac{132}{x}\) hours.
∴ Time taken by express train to cover 132 km = \(\frac{132}{x+11}\) hours.
Time taken by express train = Time taken by passenger train – 1
\(\frac{132}{x+11}=\frac{132}{x}-1\)
∴ 132x = 132(x + 11) – x(x + 11) (Multiplying by x(x + 11))
∴ 132x = 132x + 1452 – x² – 11x
∴ x² + 11x – 1452 = 0
Here, a = 1, b = 11 and c = -1452.
∴ b² – 4ac = (11)² – 4(1)(-1452)
= 121 + 5808 = 5929
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ x = \(\frac{-11 \pm \sqrt{5929}}{2(1)}\)
∴ x = \(\frac{-11 \pm 77}{2}\)
x = 33 or x = -44
x = -44 is inadmissible as x represents the speed of the passenger train.
∴ x = 33 and x + 11 = 44
Thus, the speed of the passenger train is 33 km/h and the speed of the express train is 44 km/h.

Question 11.
Sum of the areas of two squares is 468 m². If the difference of their perimeters is 24 m, find the sides of the two squares.
Solution:
Let the side of the smaller square be x m.
Then, the perimeter of the smaller square = 4x m
and the area of the smaller square = x² m².
From the given, the perimeter of the bigger square = (4x + 24) m.
∴ Side of the bigger square = \(\frac{4 x+24}{4}\) = (x + 6) m and hence, the area of the bigger square = (x + 6)² m².
∴ x² + (x + 6)² = 468
∴ x² + x² + 12x + 36 – 468 = 0
∴ 2x² + 12x – 432 = 0
∴ x² + 6x – 216 = 0
∴ x² + 18x – 12x – 216 = 0
∴ x(x + 18) – 12(x + 18) = 0
∴ (x + 18) (x – 12) = 0
∴ x + 18 = 0 or x – 12 = 0
∴ x = -18 or x = 12
Here, x = -18 is not possible as x represents the side of a square.
∴ x = 12 and x + 6 = 18
Thus, the side of the smaller square is 12 m and the side of the bigger square is 18 m.

JAC Board Class 9th Science Important Questions Chapter 13 Why Do We Fall Ill

Multiple Choice Questions

Question 1.
The disease that affects our lungs is
(a) jaundice
(b) tuberculosis
(c) scabies
(d) herpes
Answer:
(b) tuberculosis

Question 2.
The BCG vaccine provides immunity against
(a) dengue
(b) influenza
(c) ebola
(d) tuberculosis
Answer:
(d) tuberculosis

Question 3.
Malaria is caused by
(a) Anopheles mosquito
(b) Bacteria
(c) Protozoa
(d) Virus
Answer:
(a) Anopheles mosquito

Question 4.
Trypanosoma, Leishmania and Plasmodium are the examples of
(a) protozoa
(b) worms
(c) fleas
(d) viruses
Answer:
(a) protozoa

Question 5.
Diarrhoea, cholera, typhoid are the diseases that have one thing in common, which is
(a) all of them are air-borne
(b) all of them are caused by a virus
(c) all of them are caused by contaminated food and water
(d) all of them cause headache
Answer:
(c) all of them are caused by contaminated food and water

Question 6.
HIV virus attacks which one of the following cells in our body?
(a) Liver cells
(b) Neurons
(c) Nephrons
(d) White blood cells
Answer:
(d) White blood cells

Question 7.
Pathogens of disease are
(a) viruses
(b) bacteria
(c) protozoa
(d) all of the above
Answer:
(d) all of the above

Question 8.
Which of the following is a worm – caused disease?
(a) Herpes
(b) Filariasis
(c) Rabies
(d) Conjunctivitis
Answer:
(b) Filariasis

Question 9.
Which of the following is not a viral disease?
(a) AIDS
(b) Rabies
(c) Polio
(d) Tuberculosis
Answer:
(b) Rabies
(d) Tuberculosis

Question 10.
Which of the following is caused by Plasmodium parasite?
(a) Hepatitis
(b) Jaundice
(c) Tuberculosis
(d) Malaria
Answer:
(d) Malaria

Analysing & Evaluating Questions

Question 11.
If you live in an overcrowded and poorly ventilated house, you may probably suffer from which of the following diseases?
(a) Cancer
(b) AIDS
(c) Air-borne diseases
(d) Cholera
Answer:
(c) Air – borne diseases

Question 12.
During infection or injuries, inflammation of body organs occurs due to the activation of
(a) nerves
(b) muscles
(c) immune system
(d) breathing
Answer:
(c) immune system

Question 13.
Suppose you are experiencing the symptoms of cough and breathlessness. Which organ of your body do you think might be affected?
(a) Kidney
(b) Lung
(c) Heart
(d) Stomach
Answer:
(b) Lung

Assertion-Reason Questions

Directions. In the following questions, the Assertions and the Reasons have been put forward. Read the statements carefully and choose the correct alternative from the following.
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.
(B) The assertion and the reason are correct but the reason is not the correct explanation of the assertion.
(C) The assertion is true but the reason is false.
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.

1. Assertion: DPT is a triple antigen.
Reason: DPT is administered against three diseases namely diphtheria, pertussis and tetanus.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.

2. Assertion: Antibiotics are effective against both the bacteria and the viruses.
Reason:  Viruses have many biochemical mechanisms of their own.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.

3. Assertion: Male Anopheles mosquitoes do not spread malaria.
Reason: Male Anopheles mosquitoes do not feed on human blood.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.

4. Assertion: Typhoid spreads through contaminated food and water.
Reason: Typhoid can never become an epidemic in a locality.
Answer:
(C) The assertion is true but the reason is false.

5. Assertion: HIV attacks the immune system of a person.
Reason: HIV is responsible for AIDS in people infected with it.
Answer:
(B) The assertion and the reason are correct but the reason is not the correct explanation of the assertion.

Very Short Answer Type Questions

Question 1.
What do you understand by symptoms of a disease?
Answer:
Symptoms are the signs of a disease which indicate the presence of that particular disease.

Question 2.
What are acute diseases?
Answer:
Acute diseases are diseases that last for a very short period of time.

Question 3.
What are chronic diseases?
Answer:
Chronic diseases are diseases that last for a very long period of time.

Question 4.
What are infectious diseases?
Answer:
Infectious diseases are diseases that can spread from an infected person to another healthy person, e. g., ebola.

Question 5.
Name any one disease caused due to genetic abnormality.
Answer:
Sickle-cell anaemia.

Question 6.
Name two diseases caused by protozoa.
Answer:
Trichomoniasis and malaria.

Question 7.
Name two diseases each caused by bacteria, viruses and fungi.
Answer:
Bacteria – typhoid, cholera; Viruses – ebola, mumps; Fungi – Jock-itch, ringworm.

Question 8.
Write the full form of AIDS.
Answer:
Acquired Immunodeficiency Syndrome.

Question 9.
Which organism causes sleeping sickness?
Answer:
A protozoan called Trypanosoma causes sleeping sickness.

Question 10.
Name the causative agent of kala – azar?
Answer:
Leishmania.

Question 11.
Name two air-borne diseases.
Answer:
Anthrax and smallpox.

Question 12.
Name two organ specific diseases.
Answer:
Autoimmune hepatitis which affects the liver and Grave’s disease which affects the thyroid.

Question 13.
Which virus is responsible for AIDS?
Answer:
HIV virus is responsible for AIDS.

Question 14.
State the organs affected by the following diseases. jaundice, malaria, typhoid.
Answer:
Jaundice: liver; malaria – liver and RBCs; typhoid – infects the blood.

Question 15.
How do we kill microbes that enter our bodies?
Answer:
We kill disease: causing microbes with the help of medicines that block the synthesis pathways of microbes.

Question 16.
What are disease specific means of prevention?
Answer:
Disease specific means of prevention is the use of vaccine which prevents specific diseases from affecting us, e.g., tetanus vaccine, rabies vaccine, etc.

Question 17.
Why is the creation of antiviral drugs hard?
Answer:
Viruses grow inside the host and use the host cell machinery and pathways for all its biological processes. Hence, antibiotics are not able to target the virus-specific pathways. Moreover, viruses can alter their mechanisms at a very high rate, so it becomes difficult to target a specific mechanism.

Analysing & Evaluating Questions

Question 18.
Suppose your friend is suffering from severe cold and it makes him sneeze frequently heavily. What would you suggest him as a precautionary measure so that you do not become infected with the disease?
Answer:
Severe cold or cough are airborne diseases which spread through inhalation of respiratory droplets that are released by sneezing and coughing by an infected individual. Therefore, I would suggest my friend to cover his mouth while sneezing or coughing so that virus responsible for causing this disease does not infect others.

Question 19.
A person is suffering from fever and headache from quite a period of time. He is suspecting that it may be typhoid. What should he do to confirm whether it is the same disease?
Answer:
Confirmation of a particular disease can be done by undergoing proper medical check up and laboratory tests under the supervision of a doctor.

Question 20.
Suppose a person is suffering from jaundice. Whether prescribing him penicillin will be useful or not? Name the target organ for jaundice.
Answer:
No, penicillin would not be useful in the treatment of jaundice because it is a viral diseases. Target organ for jaundice is liver.

Short Answer Type Questions

Question 1.
Define health, disease, pathogens and antibiotics.
Answer:
Health. It is a state of mental, physical and social well-being.
Disease. It is the deviation from the normal healthy well-being of an individual.
Pathogens. They are disease-causing microbes, e.g., bacteria, worms, fungi, etc.
Antibiotics. These are drugs that block the biochemical pathways important to bacteria, thereby killing them.

Question 2.
What are the two main causes of a disease?
Answer:
The two main causes are immediate and contributory causes. Immediate cause-this is due to pathogens entering our bodies. Contributory cause-these are the secondary factors which allow these pathogens to enter our bodies through dirty water, contaminated food, infected surroundings, etc.

Question 3.
Define and give examples of vaccines.
Answer:
Vaccine is an antigenic substance prepared from the agent causing the disease, which is given in advance to a body to provide immunity against that specific disease, e.g., chickenpox vaccine, hepatitis vaccine, polio vaccine.

Question 4.
What is antibiotic penicillin? Give its function.
Answer:
Penicillin is a drug prepared from the fungus Penicillium, which does not allow bacteria to build its protective cell wall, thus it dies off easily. It is used to cure diseases and infections caused by bacteria.

Question 5.
A bacterium is a cell which is destroyed by an antibiotic. Our body is also made up of cells. How come antibiotics do not affect our bodies as well?
Answer:
An antibiotic blocks the biochemical pathway through which bacteria build a protective cell wall. Human body cells do not have this cell wall, so antibiotics cannot have any such effect on our body.

Question 6.
How can cholera become an epidemic in a locality?
Answer:
Cholera is a communicable disease that spreads through contaminated water and food. Let’s say, a person living in a locality contaminates the local water supply with cholera through his excreta. Now, all the people of that locality who drink that water will get infected with cholera.

Question 7.
Why are sick patients asked to take bed rest?
Answer:
Sick patients are asked to take bed rest so that they can conserve their energy which can be used to heal their recovering organs. Moreover, if they move around, there are higher chances of them getting infected with other diseases as their immune system is already weak.

Question 8.
Write a short note on malaria, its symptoms and control.
Answer:
Malaria is caused by a protozoan that lives in blood. The parasite enters our bodies when a female Anopheles mosquito, having the protozoa named Plasmodium, sucks our blood. This protozoan affects our liver and blood cells.

• Symptoms: muscular pain, headache and very high fever.
• Control: keeping the surroundings clean with no stagnant water, using mosquito repellents, use of quinine drug.

Question 9.
What is AIDS? How does a person contract AIDS?
Answer:
AIDS or Acquired Immunodeficiency Syndrome is a disease caused by the Human immuno deficiency virus. A person with AIDS has severely affected immune system. Hence, he or she dies from other diseases that thrive from the lack of Acquired WBCs in the HIV infected body.
A person contracts AIDS in the following ways:

1. Blood transfusion
2. Sexual intercourse
3. From infected mother to a baby (in the womb)
4. Sharing of needles with infected people
5. Breast feeding (if the feeder is infected).

Question 10.
Becoming infected by an infectious microbe does not always develop into a disease. Why?
Answer:
This is because our immune system is always active and when foreign particles (microbes) enter our body, the immune system instantly attacks it, trying to kill it. So, in cases where our immune system is successful in killing the infectious microbe, we don’t develop the disease it was supposed to cause.

Question 11.
(a) Why is a balanced diet necessary for maintaining a healthy body?
(b) Name two diseases caused by junk food.
Answer:
(a) A balanced diet provides all the nutrients required by our body in the correct amount. It helps to keep our immune system healthy,

(b) Two diseases caused by junk food are obesity and high blood pressure.

Analysing & Evaluating Questions

Question 12.
No polio cases have been reported from India since the last three years. On that basis, WHO has presented certification of poliofree status to India.
1. Which pathogen is responsible for causing polio in children?
2. How the principle of immunisation is implemented for eliminating polio?
3. What is OPV?
Answer:

1. Poliomyelitis virus.
2. Oral vaccines for polio are given periodically to children under five years to age to eliminate the occurrence of the disease. These vaccines are the preparations of weak forms of polio virus strains. These preparations stimulate the body to produce antibodies in response to the exposure to polio viruses. Thus, body becomes immune to the polio disease.
3. Oral Polio Vaccine.

Question 13.
Sachin’s younger brother was suffering from diarrhoea and vomiting. So he made Oral Rehydration Solution (ORS) and gave it to his brother to drink frequently. Then he thought to take him to the doctor for medical checkup.
1. What may be the cause of diarrhoea and vomiting?
2. Name the causative agents for these diseases?
3. Why Sachin gave ORS to his brother?
Answer:

1. Diarrhoea and vomiting may occur due to the consumption of contaminated food and water.
2. The causative agents for these are mainly bacteria, but some protozoa and viruses can also cause diarrhoea and vomiting.
3. Due to diarrhoea and vomiting, the body loses excess of water and other salts leading to dehydration of the body. Therefore, Sachin used his knowledge to save his brother from the discomfort of dehydration by giving him ORS.

Long Answer Type Questions

Question 1.
If someone in the family gets an infectious disease, what precautionary steps will you take to help that person recover fast and prevent other family members from getting infected?
Answer:
(a) The infected person should be kept isolated in a separate room.
(b) The surroundings and the house need to be kept clean.
(c) His (the patient) clothes and utensils should be sanitised regularly.
(d) Separate towels, sheets and blankets should be used by the patient.
(e) Clean and boiled drinking water should be given to the patient.
(f) A balanced and nutritious meal should be provided to the patient.
(g) The patient should be allowed enough rest to recover fully.

Question 2.
What are the different methods used for the treatment and prevention of diseases?
Answer:
Principles of treatment for diseases are:
(a) To reduce the symptoms of the disease.
(b) To kill the cause of the disease, i.e., to kill the disease-causing microbes like bacteria, fungi, protozoa.

Principles of prevention are:
(a) General ways: It relates to preventing exposure to the microbes, which can be done in the following ways.

1. For air – borne infections. Avoid public spaces, cover your nose while coughing and sneezing.
2. For water – borne infections. Drink safe and filtered water.
3. For vector – borne diseases. Keep the surroundings clean, cover your food and water, do not allow stagnant water to collect.
4. Self – immunity. Exercise regularly to keep your immune system strong.

(b) Specific ways: By getting vaccination, regular checkups and medications.

Question 3.
State the mode of transmission for the following diseases. malaria, AIDS, jaundice, typhoid, cholera, rabies, tuberculosis, diarrhoea, hepatitis, influenza.
Answer:

Disease	Mode of transmission
1. Malaria	Mosquito bite (female Anopheles mosquito)
2. AIDS	Infected blood, semen, mother’s milk, sharing needle of an infected person
3. Jaundice	Contaminated water
4. Typhoid	Contaminated food and water
5. Cholera	Contaminated food and water
6. Rabies	Bite of a rabid animal
7. Tuberculosis	Cough and sneeze droplets
8. Diarrhoea	Contaminated food and water
9. Hepatitis	Contaminated food and water
10. Influenza	Cough and sneeze droplets

Question 4.
(a) What causes chickenpox?
(b) State a few precautionary measures for it.
Answer:
(a) Chickenpox is caused by a virus called varicella-zoster virus,
(b) Some precautionary steps for chicken pox are.

• The infected person should avoid direct contact with people.
• His clothes should be soaked in boiling water before washing so as to kill the virus.
• Vaccination should be taken in advance to prevent the disease.

Analysing & Evaluating Questions

Question 5.
Children living in slum areas frequently suffer from symptoms such as abdominal pain, diarrhoea, loose motions, vomiting and loss of appetite.
(a) Name the target organ or organ system for the occurrence of these symptoms.
(b) Why children are frequently suffering from these symptoms?
(c) What should be done to improve the health status of these children?
Answer:
(a) The target organ or organ system for the occurrence of these symptoms is alimentary canal.

(b) These symptoms appear frequently in the children because they live in unhygienic environment where there is non availability of clean drinking water. Hence, making them prone to infections of alimentary canal.

(c) The local authorities responsible for providing public health services should be informed regarding these health problems in the children. There should be provision of clean drinking water supply and proper sanitation in the area, so that the spread of water-borne infections can be prevented.

Activity 1

• Find out what provisions are made by your local authority (Panchayat/ Municipal Corporation) for the supply of clean drinking water.
• Find out if all the people in your locality are able to access this.

Observations:

• Local authority, i.e., Municipal Corporation of our area recycles the water. Used water is treated in water treatment plants, chlorinated and supplied through pipes to people. Water taken from river is also cleaned and made potable.
• People, who live outside municipal limits use underground water, which is supposed to be safe, by drawing water through handpumps, wells and tube-wells.

Activity 2

• Rabies virus is spread by the bite of infected dogs and other animals. There are anti-rabies vaccines for both humans and animals.
• Find out the plan of your local authority for the control of rabies in your neighbourhood. Also find if these measures are adequate or not. Suggest some improvements.

Observations:

• Local authorities have plan to provide free anti-rabies vaccination at health centres, dispensaries, etc., and also catch the stray dogs. But animal loving organisations force to let them free. Pet owners are required to get anti-rabies vaccination to their dogs/ cats. But this rule is not strictly followed.
• Suggestions.
  • People should be educated through campaigns about anti-rabies vaccination for both humans and animals.
  • Stray dogs/cats/other animals should be provided with anti-rabies vaccination.
  • Pet owners should be strictly instructed to get themselves and their pets vaccinated against rabies.

Value Based Questions

Question 1.
Radha’s brother, who is 5 years old, had high fever for two days. Doctor prescribes him antibiotics. Radha hesitantly asks for the name of the disease his brother had and why he was advised to take antibiotics without any diagnosis.
1.  Is fever a disease?
2. What is the role of antibiotics?
3. What values of Radha are reflected in the above act?
Answer:

1. Fever is not a disease; it is a symptom.
2. Antibiotics are medicines advised to be taken only when the immune system of a patient is unable to fight against the microbes.
3. Radha showed moral responsibility and general awareness.

Question 2.
Jyoti was suffering from chickenpox and was advised to stay at home by her doctor. Jyoti’s friend persuades her to go for class picnic along with her and have fun. But Jyoti refuses and stays at home.
1. What is the cause of chickenpox?
2. Give one precaution for it.
3. What value of Jyoti is reflected in not going for picnic?
Answer:

1. Virus causes chickenpox.
2. One precaution for avoiding spread of chickenpox is to stay away from public places when one is suffering from it and take vaccination.
3. Jyoti showed moral responsibility and self-awareness.

JAC Class 9 Science Important Questions

JAC Board Class 9th Science Important Questions Chapter 12 Sound

Multiple Choice Questions

Question 1.
Which part of the human ear converts sound vibrations into electrical signals?
(a) Malleus
(b) Incus
(c) Tympanic membrane
(d) Cochlea
Answer:
(d) Cochlea

Question 2.
What do dolphins, bats, and tortoises use to hear the sound?
(a) Ultrasound
(b) Infrasound
(c) Both (a) and (b)
(d) None of these
Answer:
(a) Ultrasound

Question 3.
Children under the age of 5 can hear upto
(a) 25 Hz
(b) 25 kHz
(c) 20 Hz
(d) 20 kHz
Answer:
(b) 25 kHz

Question 4.
Multiple reflections of sound are used in
(a) stethoscope
(b) trumpet
(c) megaphone
(d) all of these
Answer:
(d) all of these

Question 5.
To hear a distinct echo, the time interval between the original sound and the reflected sound must be at least
(a) 0.2s
(b) 1s
(c) 2s
(d) 0.1s
Answer:
(d) 0.1s

Question 6.
Speed (v), wavelength (l) and the frequency (v) of a sound wave are related as
(a) λ = v × λ
(b) v = λ – v
(c) v = λ × v
(d) v = λ/v
Answer:
(c) v = λ × v

Question 7.
Speed of sound depends upon
(a) temperature of the medium
(b) density of the medium
(c) temperature of source producing sound
(d) temperature and density of the medium
Answer:
(d) temperature and density of the medium

Question 8.
Using which characteristic of sound can we distinguish between the sounds having same pitch and loudness?
(a) Tone
(b) Note
(c) Pitch
(d) Timber
Answer:
(d) Timber

Question 9.
Loud sound can travel a larger distance, due to
(a) higher amplitude
(b) higher energy
(c) higher frequency
(d) higher speed
Answer:
(a) higher amplitude

Question 10.
A wave in slinky travelled to and fro in 5 s. The length of the slinky is 5 m. What is the velocity of the wave?
(a) 10 m/s
(b) 5 m/s
(c) 2 m/s
(d) 25 m/s
Answer:
(b) 5 m/s

Question 11.
The reciprocal of frequency is
(a) amplitude
(b) wavelength
(c) time – period
(d) wave velocity
Answer:
(c) time – period

Question 12.
To and fro motion of an object is called
(a) wave
(b) vibrations
(c) amplitude
(d) all of the above
Answer:
(b) vibrations

Question 13.
Which of the following frequencies will be audible to the human ear?
(a) 5 Hz
(b) 5000 Hz
(c) 27000 Hz
(d) 50000 Hz
Answer:
(b) 5000 Hz

Question 14.
If the distance between a crest and its consecutive trough is L, then the wavelength of the wave is given by
(a) L
(b) 2L
(c) L/2
(d) 4L
Answer:
(b) 2L

Question 15.
What is the nature of the ocean waves in deep water?
(a) Transverse
(b) Longitudinal
(c) Both transverse and longitudinal
(d) None of these
Answer:
(c) Both transverse and longitudinal

Analysing & Evaluating Questions

Question 16.
A key of a mechanical piano is struck gently and then struck again but much harder this time. In the second case
(a) sound will be louder but pitch will not be different
(b) sound will be louder and pitch will also be higher
(c) sound will be louder but pitch will be lower
(d) both loudness and pitch will remain unaffected
Answer:
(a) sound will be louder but pitch will not be different

Question 17.
Which kind of sound is produced by an earthquake before the main shock wave begins?
(a) ultrasound
(b) infrasound
(c) audible sound
(d) none of these
Answer:
(b) infrasound

Question 18.
Before playing the orchestra in a musical concert, a sitarist tries to adjust the tension and pluck the string suitably. By doing so, he is adjusting
(a) intensity of sound only
(b) amplitude of sound only
(c) frequency of the sitar string with the frequency of other musical instruments
(d) loudness of sound
Answer:
(c) frequency of the sitar string with the frequency of other musical instruments

Assertion Reason Questions

Directions: In the following questions, the Assertions and the Reasons have been put forward. Read the statements carefully and choose the correct alternative from the following:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.
(B) The assertion and the reason are correct but the reason is not the correct explanation of the assertion.
(C) The assertion is true but the reason is false.
(D) Both the statements are false.
1. Assertion:
Sound travels as a longitudinal wave in air.
Reason: Sound wave needs a medium for its propagation.
Answer:
(B) The assertion and the reason are correct but the reason is not the correct explanation of the assertion.

2. Assertion: Speed of sound increases on increasing the temperature of the medium through which its propagates.
Reason: On increasing the temperature, kinetic energy of the particles of medium increases.
Answer:
(B) The assertion and the reason are correct but the reason is not the correct explanation of the assertion.

3. Assertion: Stage of an auditorium has a curved sound board behind the stage.
Reason: Curved wall spreads sound in all directions evenly.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.

4. Assertion: Sound travels faster in solids than in liquids.
Reason: Particles of solids are closely packed as compared to those of liquids.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.

5. Assertion: Pitch of a sound wave depends on its frequency.
Reason: Higher the frequency, lesser is the pitch of the sound wave.
Answer:
(C) The assertion is true but the reason is false.

Very Short Answer Type Questions

Question 1.
What is SONAR?
Answer:
SONAR (Sound Navigation And Ranging) is a technique used for determining water depth and locating underwater objects, such as reefs, submarines and school of fish.

Question 2.
Define one hertz.
Answer:
One hertz is one vibration per second.

Question 3.
Name the two types of mechanical waves.
Answer:
The two types of mechanical waves are:

1. Transverse wave
2. Longitudinal wave

Question 4.
What is a wave?
Answer:
A wave is a disturbance that travels in a medium due to repeated periodic motion of particles about their mean position, such that the disturbance is handed over from one particle to the other without the actual movement of the particles of the medium.

Question 5.
What is a longitudinal wave?
Answer:
It is a wave in which the particles of the medium vibrate in the direction of propagation of the wave.

Question 6.
What is a transverse wave?
Answer:
It is a wave in which the particles of the medium vibrate perpendicular to the direction of propagation of the wave.

Question 7.
What do you understand by the term ‘echo’?
Answer:
The sound heard after reflection from a rigid obstacle back to the listener is called ‘echo’.

Question 8.
What is ‘pitch’?
Answer:
The way our brain interprets the frequency of an emitted sound is called ‘pitch’.

Question 9.
What is ‘note’ of a sound?
Answer:
The sound produced due to a mixture of several frequencies is called a ‘note’.

Question 10.
What are ‘ultrasonic’ and ‘infrasonic’ sound waves?
Answer:
Sound waves with frequencies below the audible range (less than 20 Hz) are termed as ‘infrasonic sound waves’ and sound waves with frequencies above the audible range (more than 20,000 Hz) are termed as ‘ultrasonic sound waves’.

Analysing & Evaluating Questions

Question 11.
The speed of sound in vulcanised rubber is much lower than in the common solids. Give a proper explanation.
Answer:
Rubber is soft, porous and sound absorber.

Question 12.
A sound wave corresponds to larger number of compressions and rarefaction passing through a fixed point per unit of time. Should it have higher pitch or lower pitch?
Answer:
Such a sound wave will have higher pitch, (i.e., higher frequency).

Question 13.
An echo is heard on a day when temperature is about 22°C. Will the echo be heard sooner or later if the temperature falls to 4°C?
Answer:
At lower temperature, the speed of sound will decrease. Therefore, to travel through the same distance, it will take more time. So the echo will be heard later.

Short Answer Type Questions

Question 1.
What are mechanical or elastic waves? Give examples.
Answer:
The waves which require a material medium for their propagation are called f mechanical waves. They are also called elastic waves because their propagation depends on the elastic properties of the medium.

Examples of mechanical waves:
(a) Sound waves in air.
(b) Waves over water surface.
(c) Waves produced during earthquake (seismic waves).

Question 2.
What are electromagnetic waves? Cite examples.
Answer:
The waves which do not require a material medium for their propagation are called electromagnetic waves. Such waves travel through vacuum with a speed of 3 × 108 m/s.
Examples of electromagnetic waves:
(a) Light waves
(b) X – rays
(c) Radio waves
(d) Microwaves

Question 3.
Define ‘crests’ and ‘troughs’ of a wave.
Answer:
In transverse waves, the particles of the medium which have maximum displacement in the positive Y – direction are called ‘crests’ while those which have maximum displacement in the negative Y – direction are called ‘troughs’.

Question 4.
Define the terms ‘compressions’ and ‘rarefactions’.
Answer:
When longitudinal waves pass through a medium, these cause pressure variations in different parts of the medium. The regions of increased pressure are called ‘compressions’ and the regions of decreased pressure are called ‘rarefactions’.

Question 5.
Differentiate between sound and light waves.

Sound wave	Light wave
(a) Travels in the form of longitudinal wave.	(a) Travels in the form of transverse wave.
(b) Requires a medium for its propagation.	(b) Does not require a medium for its propa – gation.
(c) Travels through air with a speed of 332 m/s at 0°C.	(c) Travels through air with a speed of nearly 3 × 108 m/s.

Question 6.
Why are the longitudinal waves also called pressure waves?
Answer:
Longitudinal waves travel in a medium as a series of alternate compressions and rarefactions, i.e., as they travel, there is a variation in pressure across the medium. Therefore, they are called pressure waves.

Question 7.
Derive a relation between wavelength, frequency and velocity of a wave.
Answer:
Frequency, wavelength and wave velocity are related as follows: Wavelength is the distance travelled by the wave during the time a particle of the medium takes to complete one vibration. Therefore, if λ be the wavelength and T be the time – period, the wave travels a distance λ in time T.
Hence, Wave velocity = \(\frac{Distance}{Time}\)
⇒ v = \(\frac{\lambda}{\mathrm{T}}\)
⇒ v = λ v
∵ {\(\frac{1}{T}\) = frequency (v)}
∴ Wave velocity = Frequency × Wavelength
The wave velocity in a medium remains constant under the same physical conditions.

Question 8.
On what factor does the frequency of a wave depend?
Answer:
Frequency of a wave is given by,
v = \(\frac{\mathrm{v}}{\lambda}\)
Where,
v is the speed with which the wave propagates, and λ is the wavelength of the wave. Different sources produce oscillations of different frequencies depending on the wavelength of the sources. Frequency changes such that the speed remains constant.

Question 9.
A boat at anchor is rocked by waves whose consecutive crests are 100 m apart. The wave velocity of the mocking crests is 20 m/s. What is the frequency of rocking of the boat?
Answer:
Wavelength, λ = Distance between two successive crests = 100 m
Velocity, v = 20 m/s
Frequency, v = \(\frac{\mathrm{v}}{\lambda}\) = \(\frac{20}{100}\) = 0.20 Hz.

Question 10.
Why do the animals behave in apeculiar manner before an earthquake?
Answer:
When the earthquake strikes, it produces low frequency infrasounds before the main shock waves. These infrasonic waves are not audible to the human ears. But animals are able to detect these waves and hence some animals get disturbed before earthquakes and start behaving in a different manner.

Question 11.
Differentiate between longitudinal wave and transverse wave.
Answer:

Longitudinal wave	Transverse wave
(a) It needs a medium for propagation.	(a) It may or may not need a medium for propagation.
(b) Particles of the medium move in a direction parallel to the direction of propagation of the disturbance.	(b) Particles of the medium move in a direction perpendicular to the direction of propagation of the disturbance.
Example: Sound wave.	Examples: Light wave and seismic wave.

Question 12.
What are multiple echoes? Give examples.
Answer:
The successive reflection of a sound wave from a number of obstacles results in hearing the echo of the sound transmitted one after the other. When a sound is repeatedly reflected between two parallel distant buildings or cliffs, multiple echoes are produced. For example, rolling of thunder is due to successive reflections between clouds and land surfaces.

Question 13.
A sound wave causes the density of air at a place to oscillate 1200 times in 2 minutes. Find the time period and frequency of the wave.
Answer:
Frequency = \(\frac{1200}{2 \times 60}\) = 10 Hz.
Time period = ?
Frequency = \(\frac{1}{\mathrm{~T}}\)
T = \(\frac{1}{Frequency}\) = \(\frac{1}{10}\) = 0. 1s.

Analysing & Evaluating Questions

Question 14.
The speed of certain waves depends on the source and the medium through which they travel.
1. What kind of waves are these?
2. Give one example of the answer to (a).
Answer:

1. These waves are mechanical waves.
2. Sound waves, water waves, string waves are mechanical waves.

Question 15.
The sound of an explosion on the surface of a lake is heard by a boatman 100 m away and by a diver 100 m below the point of explosion.
1. Who will hear the sound of explosion first?
2. If sound takes time t seconds to reach the boatman, how much time (approximately) will it take to reach the diver?
Answer:
1. The diver who is 100 m below the point of explosion will hear the sound of explosion first because sound travels much faster in water than in air.

2. Time taken by sound to reach the diver
= \(\frac{ Speed of sound in air × t}{Speed of sound in Water }\)
= \(\frac{344 \mathrm{~m} \mathrm{~s}^{-1}}{1533 \mathrm{~m} \mathrm{~s}^{-1}} \times \mathrm{ts}\)
= 0.22 t seconds

Long Answer Type Questions

Question 1.
State the factors on which the speed of sound in a gaseous medium depends.
Answer:
The speed of sound in a gas depends on the following factors:
(a) Effect of density: At constant pressure, the speed of sound in a gas is inversely proportional to the square root of its density.
Speed of sound ∝ = \(\frac{1}{\sqrt{\text { Density of gas }}}\)

(b) Effect of humidity: Sound travels faster in moist air than in dry air.

(c) Effect of temperature: The speed of sound in a gas is directly proportional to the square root of its absolute temperature.
Speed of sound ∝= \(\sqrt{\text { Absolute temperature of gas }}\)
So, the speed of sound increases with the increase in temperature of the gas. For example, the speed of sound in air is 331 ms^-1 at 0°C and 344 ms^-1 at 20°C.

(d) Effect of wind: Sound is carried by air, so the speed of sound increases when the wind blows in the direction of sound and speed of sound decreases when the wind blows in the direction opposite to the direction of sound.

Question 2.
Explain some important applications of ultrasound in industry and medicine.
Answer:
Applications of ultrasound in industry and medicine are as follows:

• Industrial applications:
  1. The construction of big structures like buildings, bridges, machines, scientific equipment, etc., use metallic components.
  2. The cracks or holes inside the block reduce the strength of the structure. Such defects are not visible from outside. Ultrasonic waves can be used to detect such defects.
  3. Ultrasonic waves are allowed to pass through the metal block and detectors are used to detect the transmitted waves. If there is even a small defect, the ultrasound gets reflected back and does not reach the detector. This is how the presence of a flaw or defect is detected.
• Medical applications:

1. Echocardiography: In this technique, ultrasonic waves are made to reflect from various parts of the heart to form the image of the heart.
2. Ultrasonography: Ultrasonic waves can be used to develop three dimensional photographs of different parts of the human body. This technique is called ultrasonography.
   • This technique is also used to monitor the growth of a foetus inside its mother’s womb In this technique, the ultrasonic waves travel through the tissues of the body and get reflected from a region where there is a change of tissue density.
   • These waves are then converted into electrical signals that are used to generate images of the organ. These images are then displayed on a monitor or printed on a film.
3. In surgery: Ultrasonic waves are commonly used in cataract removal. Ultrasonic waves are also used to grind small stones formed in the kidneys. These grinded grains are flushed with urine.

Question 3.
State some important characteristics of wave motion.
Answer:
Characteristics of wave motion are as follows:

1. It is the disturbance which travels forward through the medium and not the particles of the medium. The particles of the medium merely vibrate about their mean positions.
2. Each particle receives vibrations a little later than its preceding particle.
3. The velocity with which wave travels is different from the velocity of the particles with which they vibrate about their mean positions.
4. The wave velocity remains constant in a given medium while the particle velocity changes continuously during its vibration about the mean position.

Question 4.
How can a longitudinal wave be represented graphically?
Answer:
Graphical representation of a longitudinal wave:

Sound propagates as density or pressure variations as shown in (a), (b) and (c).

1. When a longitudinal wave passes through a medium, the particles of the medium come closer together and move away from one another alternately. Thus, alternate regions of increased and decreased density are created. These regions are called compressions and rarefactions respectively.
2. The figures (a) and (b) represent the density and pressure variations, respectively, as the sound wave propagates through a medium.
   Figure (c) represents the variations of density and pressure graphically.
3. The variation of density increases or decreases as the pressure of the medium at a given time increases or decreases with distance, above and below the average value of density and pressure.
4. The distance between two successive compressions (C) or two successive rarefactions (R) is called wavelength. It is usually represented by λ (lambda).

Question 5.
Explain the formation of waves with the help of an example.
Answer:
A wave is a pattern of disturbance which travels through a medium due to repeated vibrations of the particles of the medium, the disturbance being handed over from one particle to the next. The motion of the disturbance is called wave motion. If we drop a pebble into a pond of still water, a circular pattern of alternate crests and troughs spreads out from the point where the pebble strikes the water surface. The kinetic energy of the pebble makes the particles which come in contact with it oscillate.

These particles, in turn, transfer energy to the particles of next layer which begin to oscillate. Energy is further transferred to the particles of the next layer which also begin to oscillate and so on. In this way, energy is carried by the waves from one part to another. Further, if we throw pieces of paper or a cork on the water surface, it will oscillate up and down about its mean position and will not move forward with the wave. This shows that it is the disturbance of the wave which travels forward and not the particles of the medium.

Question 6.
A ship sends out ultrasound that returns from the seabed and is detected after 4 s. If the speed of ultrasound through seawater is 1550 m/s, what is the distance of the seabed from the ship?
Answer:
Time between transmission and detection, t = 4s
Speed of ultrasound in sea water,
v = 1550 m/s
Distance travelled by the ultrasound
= 2 × depth of the sea = 2d
where d is the depth of the sea.
2d = Speed of sound × time = 1550 m/s × 4s = 6200m
d =\(\frac{6200}{2}\) m = 3100 m = 3.1 km.
Thus, the distance of the seabed from the ship is 3100 m or 3.1 km.

Analysing & Evaluating Questions

Question 7.
A sound were travelling in a medium is represented as shown in the figure

(a) Which letter represents the amplitude of the sound wave?
(b) Which letter represents the wavelength of wave?
(c) What is the frequency of the source of sound if the vibrating source of sound makes 360 oscillations in 2 minutes?
Answer:
In the figure,
(a) The amplitude is represented by X.
(b) The wavelength is represented by Y.
(c) Frequency
= \(\frac{No. of oscillations }{ Time in sec onds}\) = \(\frac{360}{2 \mathrm{~min}}\)
= \(\frac{360}{2 \times 60 \mathrm{~s}}\) = 3s^-1 = Hz

Activity-1

• Take a tuning fork and set it vibrating by striking its prong on a rubber pad. Bring it near your ear and observe.
• Touch one of the prongs of the vibrating tuning fork with your finger and see what happens.
• Take a table tennis ball or a small plastic ball Now,Take a big needle and a thread, put a knot at one end of the thread, and then with the help of the needle, pass the thread through the ball. Suspend the ball from a support. Now, touch the ball gently with the prong of a vibrating tuning fork. Observe what happens.
  

Observations

• A sound is heard on bringing the vibrating fork near the ear.
• If we touch the ball with a turning fork set into vibration, the ball gets displaced from its mean position and starts oscillating.

Activity 2

• Fill water in a beaker or a glass up to the brim. Gently touch the water surface with one of the prongs of the vibrating tuning fork, as shown in the figure.
• Next, dip the prongs of the vibrating tuning fork in water, as shown in the figure.
• Observe what happens in both the cases.
  

Observations
In both the cases, sound will be produced by the turning fork which produces ripples in water. But in case (1), ripples are produced which will move up and down and in case (2), ripples are produced which will move sideways.

Activity 3

• Take a spring. Ask your friend to hold one of its end. You hold the other end. Now stretch the slinky as shown in the figure. Then give it a sharp push towards your friend and observe.
• Move your hand pushing and pulling the slinky alternatively and observe again.
  

Observations

• When we give a small jerk, a hump is produced and this travels forward. It represents a transverse wave.
• When we give a sharp push, a continuous disturbance is produced. This disturbance starts moving in the forward and backward direction parallel to the direction of propagation of the disturbance. It represents a longitudinal wave.
• If you mark a dot on the slinky, you will observe that the dot on the slinky will move back and forth parallel to the direction of the propagation of the disturbance.

Activity 4

• Take two identical pipes, as shown in the figure. You can make pipes using a chart paper. The length of the pipes should be sufficiently long as shown.
• Arrange them on a table near a wall.
• Keep a clock near the open end of one of the pipes and try to hear the sound of the clock through the other pipe.
• Adjust the position of the pipes, so that you can hear the best sound of the clock.
• Now, measure the angles of incidence and reflection and see the relationship between the angles.
• Lift the pipe on the right, vertically to a small height and observe what happens.
  

Observations

• Reflection of sound is similar to the reflection of light, i.e., angle of incidence = angle of reflection.
• If we lift the pipe vertically to a small height, we will not be able to hear the sound through the other end of the pipe because the incident sound wave, the reflected sound wave and the normal, all he in the same plane.

Value Based Questions

Question 1.
Sahil noticed that his pet dog was frightened and trying to hide in a safe place in his house when some crackers were burst in the neighbourhood. He realised the problem and he decided not to burst crackers during diwali or for any other celebrations.
1. What must be the range of sound of crackers?
2. Name two diseases that can be caused due to noise pollution.
3. Name the values of Sahil reflected in the above act.
Answer:

1. The range of crackers sound must be between 20 Hz and 20 kHz.
2. Two diseases that can occur due to noise pollution are heart attack and high blood pressure.
3. Sahil reflects the value of respect and sensitivity for animals and caring for animals.

Question 2.
It is not advisable to construct houses near airports. Inspite of that, many new apartments are constructed near airports. Rahul files RTI and also complains to the municipal office about the same?
1. Why should we not reside near airport?
2. Name two other places where there is noise pollution.
3. What value of Rahul is reflected in this act?
Answer:

1. The landing and taking off of the airplanes cause a lot of noise pollution which may lead to deafness, high blood pressure, and other health problems.
2. The other two places where there is noise pollution are heavy traffic routes and railway stations or lines.
3. Rahul shows the values of a responsible citizen and shows awareness.

JAC Class 9 Science Important Questions

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 Quadratic Equations Ex 4.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 Quadratic Equations Exercise 4.2

Question 1.
Find the roots of the following quadratic equations by factorisation:
1. x² – 3x – 10 = 0
2. 2x² + x – 6 = 0
3. \(\sqrt{2}\)x² + 7x + 5\(\sqrt{2}\) = 0
4. 2x² – x + \(\frac{1}{8}\) = 0
5. 100x² – 20x + 1 = 0
Solution:
1. x² – 3x – 10 = 0
∴ x² – 5x + 2x – 10 = 0
∴ x(x – 5) + 2(x – 5) = 0
∴ (x – 5)(x + 2) = 0
Hence, x – 5 = 0 or x + 2 = 0
∴ x = 5 or x = -2
Thus, the roots of the given equation are 5 and -2.
Verification:
For x = 5,
LHS = (5)² – 3(5) – 10
= 25 – 15 – 10
= 0
= RHS
For x = -2,
LHS = (2)² – 3(-2) – 10
= 4 + 6 – 10
= 0
= RHS
Hence, both the roots are verified.
Note that verification is not a part of the solution. It is meant only for your confirmation of receiving correct solution.

2. 2x² + x – 6 = 0
∴ 2x² + 4x – 3x – 6 = 0
∴ 2x (x + 2) – 3(x + 2) = 0
∴ (x + 2) (2x – 3) = 0
∴ x + 2 = 0 or 2x – 3 = 0
∴ x = -2 or x = \(\frac{3}{2}\)
Thus, the roots of the given equation are -2 and \(\frac{3}{2}\)

3. \(\sqrt{2}\)x² + 7x + 5\(\sqrt{2}\) = 0
∴ \(\sqrt{2}\)x² + 2x + 5x + 5\(\sqrt{2}\) = 0
∴ \(\sqrt{2}\)x(x + \(\sqrt{2}\)) + 5(x + \(\sqrt{2}\)) = 0
∴ (x + \(\sqrt{2}\))(\(\sqrt{2}\)x + 5) = 0
∴ x + \(\sqrt{2}\) = 0 or \(\sqrt{2}\)x + 5 = 0
∴ x = –\(\sqrt{2}\) or x = \(-\frac{5}{\sqrt{2}}\)
Thus, the roots of the given equation are –\(\sqrt{2}\) and \(-\frac{5}{\sqrt{2}}\)

4. 2x² – x + \(\frac{1}{8}\) = 0
∴ 16x² – 8x + 1 = 0 (Multiplying by 8)
∴ 16x² – 4x – 4x + 1 = 0
∴ 4x(4x – 1) -1 (4x – 1) = 0
∴ (4x – 1) (4x – 1) = 0
∴ 4x – 1 = 0 or 4x – 1 = 0
∴ x = \(\frac{1}{4}\) or x = \(\frac{1}{4}\)
Thus, the repeated roots of the given equation are \(\frac{1}{4}\) and \(\frac{1}{4}\)

5. 100x² – 20x + 1 = 0
100x² – 10x – 10x + 1 = 0
10x(10x – 1) -1 (10x – 1) = 0
(10x – 1)(10x – 1) = 0
10x – 1 = 0 or 10x – 1 = 0
x = \(\frac{1}{10}\) or x = \(\frac{1}{10}\)
Thus, the repeated roots of the given equation are \(\frac{1}{10}\) and \(\frac{1}{10}\).

Question 2.
Solve the problems given in Textual Examples:
1. John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. Find out how many marbles they had to start with.
2. A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was ₹ 750. Find out the number of toys. produced on that day.
Solution:
1. Let the number of marbles that John had be x.
Then, the number of marbles that Jivanti had is (45 – x).
After losing 5 marbles, the number of marbles left with John = x – 5.
After losing 5 marbles, the number of marbles left with Jivanti = (45 – x) – 5 = 40 – x.
Therefore, the product of marbles with them is (x – 5) (40 – x), which is given to be 124.
Hence, we get the following equation:
(x – 5)(40 – x) = 124.
∴ 40x – x² – 200 + 5x = 124
∴ -x² + 45x – 324 = 0
∴ x² – 45x + 324 = 0
∴ x² – 36x – 9x + 324 = 0
∴ x(x – 36) – 9(x – 36) = 0
∴ (x – 36)(x – 9) = 0
∴ x – 36 = 0 or x – 9 = 0
∴ x = 36 or x = 9
Here, both the answers are admissible.
∴ 45 – x = 45 – 36 = 9 or
45 – x = 45 – 9 = 36
Thus, the number of marbles with John and Jivanti to start with are 36 and 9 respectively or 9 and 36 respectively.

2. Let the number of toys produced on that day be x.
Therefore, the cost of production (in rupees) of each toy on that day = 55 – x.
So, the total cost of production (in rupees) on that day = x (55 – x).
Hence, x(55 – x) = 750
∴ 55x – x² – 750 = 0
∴ x² – 55x + 750 = 0
∴ x² – 30x – 25x + 750 = 0
∴ x(x – 30) – 25(x – 30) = 0
∴ (x – 30)(x – 25) = 0
∴ x – 30 = 0 or x – 25 = 0
∴ x = 30 or x = 25
Here, both the answers are admissible.
Hence, the number of toys produced on that day is 30 or 25.

Question 3.
Find two numbers whose sum is 27 and product is 182.
Solution:
Let the first of the two numbers whose sum is 27 be x.
Then, the second number is 27 – x and the product of those two numbers is x (27 – x).
Their product is given to be 182.
∴ x (27 – x) = 182
∴ 27x – x² – 182 = 0
∴ x² – 27x + 182 = 0
∴ x² – 14x – 13x + 182 = 0
∴ x(x – 14) – 13(x – 14) = 0
∴ (x – 14)(x – 13) = 0
∴ x – 14 = 0 or x – 13 = 0
∴ x = 14 or x = 13
Here, both the answers are admissible.
Hence, if x = 14, it gives that the first number = x = 14 and the second number = 27 – x = 27 – 14 = 13.
And if x = 13, it gives that the first number = x = 13 and the second number = 27 – x = 27 – 13 = 14.
Thus, in either case, the required numbers are 13 and 14.

Question 4.
Find two consecutive positive integers, sum of whose squares is 365.
Solution:
Let two consecutive positive integers be x and x + 1.
Then, the sum of their squares = (x)² + (x + 1)²
= x² + x² + 2x + 1
= 2x² + 2x + 1
This sum is given to be 365.
∴ 2x² + 2x + 1 = 365
∴ 2x² + 2x – 364 = 0
∴ x² + x – 182 = 0
∴ x² + 14x – 13x – 182 = 0
∴ x(x + 14) – 13(x + 14) = 0
∴ (x + 14)( x- 13) = 0
∴ x + 14 = 0 or x – 13 = 0
∴ x = -14 or x = 13
Since x is a positive integer, x = -14 is inadmissible.
∴ x = 13 and x + 1 = 13 + 1 = 14
Thus, the required consecutive positive integers are 13 and 14.

Question 5.
The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Solution:
Let the base of the right triangle be x cm.
Then, its altitude is (x – 7) cm.
The hypotenuse of the right triangle is given to be 13 cm.
Now, by Pythagoras theorem.
(Base)² + (Altitude)² = (Hypotenuse)²
∴ (x)² + (x – 7)² = (13)²
∴ x² + x² – 14x + 49 = 169
∴ 2x² – 14x – 120 = 0
∴ x² – 7x – 60 = 0
∴ x² – 12x + 5x – 60 = 0
∴ x(x – 12) + 5(x – 12) = 0
∴ (x – 12)(x + 5) = 0
∴ x – 12 = 0 or x + 5 = 0
∴ x = 12 or x = -5
As the base of a triangle cannot be negative. x = -5 is inadmissible.
Hence, x = 12.
Then, the base of the triangle = x = 12 cm and the altitude of the triangle = x – 7 = 12 – 7
= 5 cm.
Thus, the base and the altitude of the given triangle are 12 cm and 5 cm respectively.

Question 6.
A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was 90. find the number of articles produced and the cost of each article.
Solution:
Let the number of pottery articles produced on that day be x.
Then, according to the given, the cost of production (in rupees) of each article = 2x + 3.
Hence, total cost of production (in rupees) on that day = x(2x + 3) = 2x² + 3x.
This total cost of production is given to be ₹ 90.
∴ 2x² + 3x = 90
∴ 2x² + 3x – 90 = 0
∴ 2x² – 12x + 15x – 90 = 0
∴ 2x(x – 6) + 15(x – 6) = 0
∴ (x – 6) (2x + 15) = 0
∴ x – 6 = 0 or 2x + 15 = 0
∴ x = 6 or x = –\(\frac{15}{2}\)
Here, x = –\(\frac{15}{2}\) is inadmissible as x represents the number of articles produced.
Hence, x = 6 and 2x + 3 = 2(6) + 3 = 15.
Thus, the number of pottery articles produced on that day is 6 and the cost of production of each article is ₹ 15.

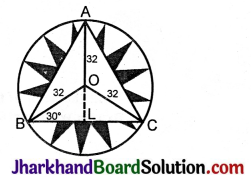
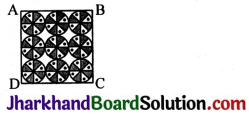
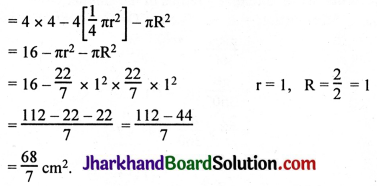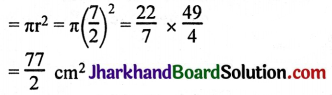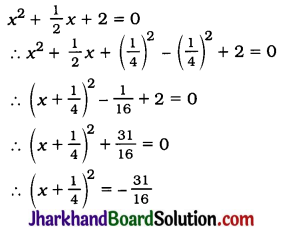JAC Board Class 9th Science Important Questions Chapter 1 Matter in Our Surroundings

Multiple Choice Questions

Question 1.
Evaporation of a liquid occurs at
(a) boiling point
(b) a fixed temperature
(c) temperature lower than boiling point
(d) all temperatures
Answer:
(c) temperature lower than boiling point

Question 2.
Intermolecular force of attraction is maximum in
(a) Solids
(b) Liquids
(c) Gases
(d) Plasma particles
Answer:
(a) Solids

Question 3.
………… will not exhibit diffusion.
(a) Hydrogen and oxygen
(b) Oxygen and water
(c) Salt and sand
(d) Sugar crystal and water
Answer:
(c) Salt and sand

Question 4.
Which of the following substances is not a solid?
(a) Air
(b) Butter
(c) Sponge
(d) Rubber band
Answer:
(a) Air

Question 5.
Which one of the following properties is not a characteristic of liquids?
(a) Fluidity
(b) Definite shape
(c) Definite volume
(d) Compressibility
Answer:
(b) Definite shape

Question 6.
Fusion is the process in which
(a) liquid changes into gas
(b) solid changes into liquid
(c) solid changes into gas
(d) gas changes into solid
Answer:
(b) solid changes into liquid

Question 7.
The density of water is maximum at
(a) 0°C
(b) 100°C
(c) 4°C
(d) 273K
Answer:
(c) 4°C

Question 8.
Choose the correct statement from the following:
(a) Two gases cannot diffuse into each other.
(b) The volume of gas expands on heating.
(c) Conversion of a gas into solid is called condensation.
(d) Gases cannot diffuse in solids.
Answer:
(b) The volume of gas expands on heating.

Question 9.
Which among the following can exist in vapour state?
(a) Oxygen
(b) Hydrogen
(c) Carbon dioxide
(d) Water
Answer:
(d) Water

Question 10.
Cooking of rice at higher altitudes is difficult because
(a) water boils at temperature <100°C
(b) water boils at 100°C
(c) boiling point of water is constant
(d) none of the above
Answer:
(a) water boils at temperature <100°C

Question 11.
At normal pressure, the boiling point of water is
(a) 98°C
(b) 100°C
(c) 110°C
(d) 90°C
Answer:
(b) 100°C

Question 12.
Gases do not have
(a) high compressibility
(b) high fluidity
(c) high density
(d) volume
Answer:
(c) high density

Question 13.
Molecules of a liquid
(a) have very strong intermolecular forces
(b) cannot move randomly
(c) have definite shape
(d) have large intermolecular spaces
Answer:
(d) have large intermolecular spaces

Question 14.
………….. decreases the rate of evaporation.
(a) Surface area
(b) Humidity
(c) Temperature
(d) Wind
Answer:
(b) Humidity

Question 15.
…………… does not convert a liquid into vapours.
(a) Boiling
(b) Evaporation
(c) Heating
(d) Condensation
Answer:
(d) Condensation

Analysing & Evaluating Questions

Question 16.
Seema visited a Natural Gas Compressing Unit and found that the gas can be liquefied under specific conditions of temperature and pressure. While sharing her experience with friends, she got confused. Help her to identify the correct set of conditions for liquefaction of gases.
(a) Low temperature, low pressure
(b) High temperature, low pressure
(c) Low temperature, high pressure
(d) High temperature, high pressure
Answer:
(c) Low temperature, high pressure

Question 17.
Under which of the following conditions, the distance between the molecules of hydrogen gas would increase?
I. Increasing pressure on hydrogen contained in a closed container.
II. Some hydrogen gas leaking out of the container.
III. Increasing the volume of the container of hydrogen gas.
IV. Adding more hydrogen gas to the container without increasing the volume of the container.
(a) I and III
(b) I and IV
(c) II and III
(d) II and IV
Answer:
(c) II and III

Question 18.
A substance has a definite shape, fixed volume, distinct boundary and cannot be compressed. What is the physical state of this substance?
(a) Solid
(b) Liquid
(c) Gas
(d) Plasma
Answer:
(a) Solid

Assertion – Reason Questions

Directions: In the following questions, the Assertions and the Reasons have been put forward. Read the statements carefully and choose the correct alternative from the following:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.
(B) The assertion and the reason are correct but the reason is not the correct explanation of the assertion.
(C) The assertion is true but the reason is false.
(D) Both statements are false.
1. Assertion: Gases diffuse faster than liquids.
Reason: Particles of gases have higher kinetic energy than those of liquids.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.

2. Assertion: Solids have negligible compressibility.
Reason: In solids, the intermolecular force of attraction is very strong.
Answer:
(B) The assertion and the reason are correct but the reason is not the correct explanation of the assertion.

3. Assertion: Evaporation always takes place at the surface of a liquid.
Reason: Molecules at the surface of liquids have higher temperature.
Answer:
(C) The assertion is true but the reason is false.

4. Assertion: On heating or cooling, the physical state of a substance gets changed.
Reason: State of matter can be changed only by changing its temperature.
Answer:
(C) The assertion is true but the reason is false.

5. Assertion: Solids generally lack the property of diffusion.
Reason: In solids, intermolecular space is negligible.
Answer:
(A) Both the assertion and the reason are correct and the reason is the correct explanation of the assertion.

Very Short Answer Type Questions

Question 1.
What is matter?
Answer:
Anything that has mass and occupies space is called matter. For examples, rocks, plants, paper. chalk, water, food. etc.

Question 2.
In what ways are all substances around us alike?
Answer:
All the substances are matter, i.e., they all have mass and occupy space. Therefore, they are all alike.

Question 3.
Why is the rate of diffusion faster in gases?
Answer:
Because the intermolecular force of attraction is minimum in gases.

Question 4.
Why are light and sound not considered as matter?
Answer:
Light and sound are not considered as matter because they have no mass and they do not occupy space.

Question 5.
Name the three states of matter.
Answer:
Solid, liquid and gas are the three states of matter.

Question 6.
Ice and water are basically the same substance. Mention two differences in their properties.
Answer:

1. Ice: It has fixed volume and definite shape. It can be stored without a container.
2. Water: It is a liquid and has no definite shape. It cannot be stored without a container.

Question 7.
Classify the following materials according to the state in which they exist around us. Steel, blood, air, oil, rubber, honey, carbon dioxide, kerosene, LPG, CNG, nitrogen, oxygen
Answer:

• Solid: Steel, rubber.
• Liquid: Blood, oil, honey, kerosene, LPG.
• Gas: Air, carbon dioxide. CNG. nitrogen. oxygen.

Question 8.
Defineeflne boiling point.
Answer:
Boiling point ofa liquid is the temperature at which its pressure becomes equal to that of the atmospheric pressure and it starts vaporising into gaseous state.

Question 9.
Define melting point.
Answer:
The temperature at which a solid starts melting to become a liquid at atmospheric pressure is known as its melting point.

Question 10.
Latent heat of vaporisation of two liquids A and B is 100 kg and 150 kg respectively. What does It indicate?
Answer:
Latent heat of vaporisation depends on the nature of the liquid. Intermolecular

Question 11.
Which of the following shows the phenomenon of sublimation? Solid water, solid carbon dioxide, solid alcohol, solid oxygen
Answer:
Solid carbon dioxide.

Question 12.
How does spreading of wet clothes quicken their drying? Explain.
Answer:
Spreading of wet clothes increases surface area and so evaporation becomes faster. Thus, drying of wet clothes becomes faster by spreading them.

Question 13.
How does temperature affect the rate of evaporation?
Answer:
With increase of temperature, more number of particles get enough kinetic energy to change into the vapour state. Hence, rate of evaporation increases with increase in temperature.

Question 14.
Which will have more impact on kinetic energy: doubling mass or velocity?
Answer:
Doubling of velocity will increase kinetic energy four times. (KE = \(\frac{1}{2}\) mv²)

Question 15.
What is dry ice?
Answer:
Solid carbon dioxide obtained by cooling and applying pressure on carbon dioxide gas is called dry ice. it does not melt but directly transforms into vapour state, so it is called dry ice.

Question 16.
What is humidity?
Answer:
The air which holds water vapour is called humid air and the amount of water vapour present in the air is called humidity.

Question 17.
Define atmospheric pressure.
Answer:
The pressure exerted by the earth’s atmosphere at any given point is known as atmospheric pressure. The atmospheric pressure at sea level is atmosphere and is taken as the normal atmospheric pressure.

Analysing & Evaluating Questions

Question 18.
Alka was making tea in a kettle. Suddenly, she felt intense heat from the puff of steam gushing out of the spout of the kettle. She wondered whether the temperature of the steam was higher than that of the water boiling in the kettle. Comment.
Answer:
Temperature of steam is the same as that of boiling water. Intense heat of the steam is due to its high latent heat.

Question 19.
The energy changes in the following transformation are as follows:

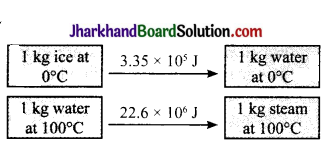
In which of the above, the intennolecu lar forces are stronger?
Answer:
The intermolecular forces are stronger in water at 100°C.

Question 20.

You are given the following substances with their melting and boiling points.

Substance	Melting Boiling point (°C)	point (°C)
X	10	25
Y	50	90
Z	15	80

Identify the physical states of X,Y and Z t the temperature of 30°C.
Answer:
‘X’ is gas at the given temperatLire.
‘Y’ is solid at the given temperature.
‘Z’ is liquid at the given temperature.

Short Answer Type Questions 

Question 1.
Common salt and sugar hase similar appearance. Why are these classified as different substances?
Answer:
The substances are not classified only by their appearance. They are classified by their properties. such as density boiling point or melting point, conductivity ther mal capacit’ and other physical and chem ical properties. Common salt and sugar have diflì.rent physical and chemical prop erties and so are different substances.

Question 2.
Why do we sec water droplets collected on the outer surface of a glass container, containing Ice?
Answer:
The water vapour present in air, comes in contact with the cold outer surface of the container and gets condensed. This causes formation of water droplets.

Question 3.
liquids and gases can be compressed hut it is difficult to compress solids. Why?
Answer:
Liquids and gases have large intermolecular space. Thus on applying pressure externally on them, the molecules can corne more close, thereby minimising the space between them. But in case of solids there is no intermolecular space to do so.

Question 4.
If you open a bottle of perfume in one comer of a room, it immediately spreads throughout the room. Explain the properly insols-ed.
Answer:
The property involved is diffusion. In a gas, the particles arc free to mese an a chaotic motion at a great speed throughout its containing vessel. Thus, when you opcn a bottle of perfume in one corner, the particles of the perfume move at random motion in all directions and mix with othergas particles in the air. Thus, they reach instantaneously to our nose.

Question 5.
Why do people perspire a lot on a hot humid day?
Answer:
On a humid day. due to the heat, our body starts sweating for thecooling mechanism by evaporation. However, the humid air cannot hold any more water on a humid das and therefore the rate of evaporation decreases. Hence. sweat or perspiration is seen.

Question 6.
Hoss does the rate of diffusion change with (a) density of liquid and (b) temperature? Gise examples.
Answer:
(a) Rate of diffusion decreases with density of s liquid. Honey is denser than ink. If you add a drop of ink and honey ‘n two separate jars filled with water, it will be ohscned that honey takes longer time to reach the bottom of the jar than by the ink.

(b) Diffision increases with rise of iempersture. For example, liquids mix faster at higher temperaiures.

Question 7.
How do you differentiate between solids, liquids and gases on the basis of their inciting poInts 2nd boiling points?
Answer:

• Solids: They hase melting and boiling points abose room temperature.
• Liquids: They hase melting pointa below room temperature and boiling point abose room temperature.
• Gases: They have both melting and boiling points below room temperature.

Question 8.
Which property of the gas is utilised when natural gas is supplied for vehicles?
Answer: A gas is highly compressible and a large quantity of it can be compressed to a small volume. Therefore, natural gas is compressed and is supplied for use by vehicles in the form ofCNG (Compressed Natural Gas).

Question 9.
On a hot das, why do people sprinkle waler on (be roof or open ground?
Answer:
On a bot das, the surface of roof or ground absorbs large amount of heat and remains bot. On sprinkling water on these surfaces, the water absorbs large amount of heai from 11w surface due to its high laient heat of sapsietsation and ewaporates. thereby allowing the hot surface to cool.

Question 10.
Esplain how dIffusion nf gases In water is essenilal?
Answer:
The gases from the atmosphere diffuse and dissolve in water. Difluasion of gases like oxygen and carbon dioxide ¡n water is essential for tIse survival ni aquatic animals and plants! Aninsals breathe – in this oxygen dissolved in watet foe their survival and planis can use carbon dioxide
dissolved in water foe photosynthesis.

Question 11.
Why are liqnids and gases called fluids?
Answer:
Liquids and gases can flow. Liquids can flow from higher pressure to lower pressure. The gases flow in all available directions. Due to this property of flowing, both of them are called fluids.

Question 12.
On a hot day, why do we feel pleasant sitting under a tree?
Answer:
Trees have a lot of leaves which constantly show transpiration. Transpiration is the loss of water through tiny pores of leaves called stomata. When this water comes on the surface of leaf the water evaporates, thereby causing a cooling effect. Therefore, we feel pleasant sitting under the tree on a hot sunny day.

Question 13.
How is the high compressibilit property of gas useful to us?
Answer:
The gases have high compressibility. This property is used in the following
situations:

1. LPG is a fuel which is made up of petroleum gas. On compressing this petroleum gas. it forms liquid.
2. Oxygen cylinders in the hospitals have compressed gas filled in it.
3. CNG is a natural gas, which is compressed and used as a fuel in vehicles.

Question 14.
What ¡s pressure? What is its unit? On what factor does the pressure of a gas depend?
Answer:
The pressure exerted by a gas is the force exerted by gas particles per unit area on the walls of the container. It is expressed in pascal (Pa). I atmosphere 101325 x 10 Pa. The pressure depends on the average kinetic energy of the particles which depends on temperature of the gas.

Question 15.
How would you show that the three states of matter are interchangeable?
Answer:
On heating a solid substance and then cooling the vapour formed, we can show that the three states of matter arc interchangeable. Take ice cubes in a beaker and heat. Ice changes into water. On further heating, water changes into steam. On cooling, water vapour again changes into water and on further cooling water changes to ice.

Question 16.
Chee freezes at room temperature but mustard oil does not freeze even in winters. Which of these has a higher melting point and lower intermolecular forces?
Answer:
Ghee freezes at room temperature but mustard oil does not, it shows that intermolecular forces in ghee are stronger than those in mustard oil. The higher the intermolecular forces, the higher is the melting point. Therefore, ghce has a higher melting point than that of mustard oil.

Question 17.
Define evaporation.
Answer:
The phenomenon of change of a liquid into vapours at any temperature below its boiling point is called evaporation. Water, if left in an open vessel at room temperature, disappears after some time due to evaporation.

Question 18.
Is it true to say that fluorescent tubes contain only plasma?
Answer:
It is not correct to say that fluorescent tube contains only plasma. Inside a fluorescent tube there is helium gas or some other gas. The gas gets ionised or charged when electrical energy flows through it.

Analysing & Evaluating Questions

Question 19.
A sample of water under study was found to boil at 102°C at normal pressure. It the water pure? Will this water freeze at 0°C? Comment.
Answer:
(a) The given sample of water is not pure.
(b) The given sample of water will not freeze 0°C. The impurities raise the boiling point and lower the freezing point of water. Therefore, the given sample of water will freeze below 0°C.

Question 20.
A strong smelling gas ¡s stored in cylinders as liquid, but it comes out of the cylinder as gas.
(a) Name the gas.
(b) Vhat causes this change in state?
(c) Name the process of this conversion.
Answer:
(a) LPG (Liquefied Peroleum Gas).
(b) LPG gets converted into gas due to lowering of pressure.
(c) Vaporisation.

Long Answer Type Questions

Question 1.
Discuss the factors which affect evaporation.
Answer:
1. Surface area: Evaporation is a surface phenomenon. Thus, escaping of particles from liquid state to vapour state depends on surface area. Therefore, the rate of evaporation increases with surface area.

2. Temperature: If the temperature is increased, the rate of evaporation also increases. Due to increase in temperature, the particles gain more kinetic energy and change their phase from liquid to gaseous. Water will evaporate faster in sun than in shade.

3. Humidity: Humidity is the amount of water vapour present in the air. At a given temperature, air cannot hold more than a fixed amount of water vapour. Therefore, the rate of evaporation decreases with increase in the humidity of air.

4. Wind speed: With the increase in wind speed, the rate of evaporation increases. The particles of water vapour move away with the wind, decreasing the amount of water vapour in the surroundings.

Question 2.
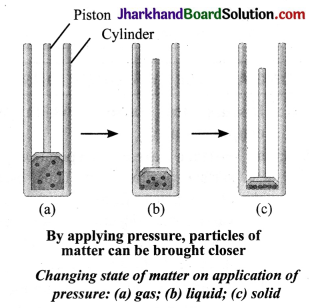
How are particles of matter affected with increasing or decreasing pressure on the matter at a given temperature?
Answer:
On increasing pressure, particles of a matter come closer and move apart when pressure is reduced at a given temperature. Thus, if pressure is increasingly applied on a gas, particles of the gas come closer and closer and eventually the gas may change into liquid and then into solid form.

Question 3.
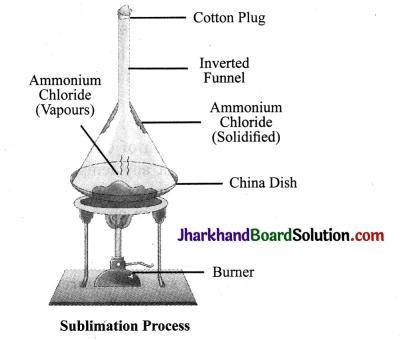
What is sublimation? With the help of an activity describe the sublimation of a solid substance. Name two substances used in our daily life that sublime on heating.
Answer:
We know that matter changes its state on heating from solid to liquid and from liquid to gas. However, there are some substances that change directly from solid state to gaseous state. This change of state from solid to gas without changing into liquid state is called sublimation. For example, camphor and ammonium chloride on heating change directly into vapour.

Activity

Take some ammonium chloride. Powder it and put in a china dish. Cover the china dish with an inverted funnel. Take some cotton and plug the stem of the funnel. Now, heat the china dish.
You will observe fine crystal particles depositing on the innerwalls ofthe funnel. Thus on heating, ammonium chloride is directly converted into ammonium chloride vapours which condense on the inner walls of the china dish.

Question 4.
Explain the diffusion of copper sulphate solution into water.
Answer:
The copper sulphate crystals dissolve slowly and form a layer of copper sulphate solution in the beaker. This blue copper sulphate solution diffuses into clear water and clear water diffuses down towards blue solution. This diffusion goes on until the whole water turns blue. So the spreading of blue colour is due to the diffusion of the blue copper sulphate solution and water into each other.

JAC Class 9 Science Important Questions

Jharkhand Board JAC Class 10 Maths Solutions Chapter 5 Arithmetic Progressions Ex 5.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 5 Arithmetic Progressions Exercise 5.1

Question 1.
In which of the following situations, does the list of numbers involved make an arithmetic progression, and why?
1. The taxi fare after each km, when the fare is ₹ 15 for the first km and ₹ 8 for each additional km.
2. The amount of air present in a cylinder when a vacuum pump removes \(\frac{1}{4}\) of the air remaining in the cylinder at a time.
3. The cost of digging a well after every metre of digging, when it costs ₹ 150 for the first metre and rises by ₹ 50 for each subsequent metre.
4. The amount of money in the account every year, when ₹ 10,000 is deposited at compound interest at 8% per annum.
Solution:
1. Here, the fare for 1 km = ₹ 15
the fare for 2 km = ₹ 15 + ₹ 8 = ₹ 23,
the fare for 3 km = ₹ 15 + 2 (₹8) = ₹ 31,
the fare for 4 km = ₹ 15 + 3 (₹8) = ₹ 39, and so on.
The list of numbers formed is 15, 23, 31, 39, …………..
Here, a₂ – a₁ = 23 – 15 = 8.
a₃ – a₂ = 31 – 23 = 8.
a₄ – a₃ = 39 – 31 = 8, and so on.
Thus, a_k+1 – a_k is the same every time.
Hence, the list of numbers forms an AP with a = 15 and d = 8.

2. Let the volume of air present in the cylinder at the beginning be V units. Then, volume of air remaining in the cylinder after first attempt = \(\frac{3}{4}\)V units. Also, volume of air remaining in the cylinder after second attempt = \(\left(\frac{3}{4}\right)^2\)V units. Here, the list of numbers formed is V, \(\frac{3}{4}\)V, \(\left(\frac{3}{4}\right)^2\)V, ………
Now, a₂ – a₁ = \(\frac{3}{4}\)V – V = –\(\frac{1}{4}\)V
a₃ – a₂ = \(\left(\frac{3}{4}\right)^2\)V – \(\frac{3}{4}\)V
= \(V\left(\frac{9}{16}-\frac{3}{4}\right)\)
= \(– \frac{3}{16}\)V
Here, a₂ – a₁ ≠ a₃ – a₂.
Hence, the list of numbers does not form an AP.

3. Cost of digging first metre = ₹ 150
Cost of digging the second metre = ₹ 150 + ₹ 50
= ₹ 200
Cost of digging the third metre = ₹ 200 + ₹ 50
= ₹ 250
Cost of digging the fourth metre = ₹ 250 + ₹ 50
= ₹ 300
The list of numbers formed is 150, 200, 250, 300,…
Here, a₂ – a₁ = 200 – 150 = 50,
a₃ – a₂ = 250 – 200 = 50,
a₄ – a₃ = 300 – 250 = 50, and so on.
Thus, a_k+1 – a_k is the same every time. Hence, the list of numbers forms an AP with a = 150 and d = 50.

4. The formula of compound interest is known to us.
A = \(P\left(1+\frac{R}{100}\right)^T\)
Here, P = ₹ 10,000; R = 8% and T = 1, 2, 3, 4, ……….
Amount at the end of 1st year = ₹ 10000 (1.08).
Amount at the end of 2nd year = ₹ 10000 (1.08)².
Amount at the end of 3rd year = ₹ 10000 (1.08)³.
The list of numbers formed is 10000 (1.08), 10000 (1.08)2, 10000 (1.08), ………..
a₂ – a₁ = 10000 (1.08)² – 10000 (1.08)³
= 10000 (1.08) (1.08 – 1)
= 10000 (1.08) (0.08)
a₃ – a₂ = 10000 (1.08)³ – 10000 (1.08)²
= 10000 (1.08)² (1.08 – 1)
= 10000 (1.08)² (0.08)
Thus, a₂ – a₁ ≠ a₃ – a₂
Hence, the list of numbers does not form an AP.

Question 2.
Write first four terms of the AP when the first term a and the common difference d are given as follows:
1. a = 10, d = 10
2. a = -2, d = 0
3. a = 4, d = -3
4. a = -1, d = \(\frac{1}{2}\)
5. a = -1.25, d = -0.25
Solution:
1. a = 10, d = 10
First term a = 10
Second term = First term + d
= 10 + 10 = 20
Third term = Second term + d
= 20 + 10 = 30
Fourth term = Third term + d
= 30 + 10 = 40
Thus, the required first four terms of the AP are 10, 20, 30, 40.

2. a = -2, d = 0
First term = a = -2
Second term = First term + d
= -2 + 0 = -2
Third term = Second term + d
= -2 + 0 = -2
Fourth term = Third term + d
= -2 + 0 = -2
Thus, the required first four terms of the AP are -2, -2, -2, -2.

3. a = 4, d = -3
First term = a = 4
Second term = First term + d
= 4 + (-3) = 1
Third term = Second term + d
= 1 + (-3) = -2
Fourth term = Third term + d
= (-2) + (-3) = -5
Thus, the required first four terms of the AP are 4, 1, -2, -5.

4. a = -1, d = \(\frac{1}{2}\)
First term = a = -1
Second term = First term + d
= -1 + \(\frac{1}{2}\) = –\(\frac{1}{2}\)
Third term = Second term + d
= \(-\frac{1}{2}+\frac{1}{2}\) = 0
Fourth term = Third term + d
= 0 + \(\frac{1}{2}\) = \(\frac{1}{2}\)
Thus, the required first four terms of the AP are -1, – \(\frac{1}{2}\), 0, \(\frac{1}{2}\).

5. a = -1.25, d = -0.25
The general form of an AP is a, a + d, a + 2d, a + 3d, …….. Then,
First term = a = -1.25
Second term = a + d
= -1.25 + (-0.25) = -1.50
Third term = a + 2d
= -1.25 + 2(-0.25) = -1.75
Fourth term = a + 3d
= -1.25 + 3(-0.25) = -2.00
Thus, the required first four terms of the AP are -1.25, -1.50, -1.75, -2.00.

Question 3.
For the following APs, write the first term and the common difference:
1. 3, 1, 1, -3, ……..
2. -5, -1, 3, 7, …….
3. \(\frac{1}{3}, \frac{5}{3}, \frac{9}{3}, \frac{13}{3}, \ldots\)
4. 0.6, 1.7, 2.8, 3.9, …
Solution:
1. 3, 1, -1, -3,….
First term a = 3
Common difference d = a₂ – a₁ = 1 – 3 = -2

2. -5, 1, 3, 7,…..
First term a = -5
Common difference d = (-1) – (-5) = 4

3. \(\frac{1}{3}, \frac{5}{3}, \frac{9}{3}, \frac{13}{3}, \ldots\)
First term a = \(\frac{1}{3}\)
Common difference d = \(\frac{5}{3}-\frac{1}{3}=\frac{4}{3}\)

4. 0.6, 1.7, 2.8, 3.9, ……
First term a = 0.6
Common difference d = 1.7 – 0.6 = 1.1

Question 4.
Which of the following are APs? If they form an AP find the common difference d and write three more terms:
1. 2, 4, 8, 16, …….
2. 2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), …….
3. -1.2, -3.2, -5.2, -7.2, …….
4. -10, -6, -2, 2, …….
5. 3, 3 + 2\(\sqrt{2}\), 3 + 2\(\sqrt{2}\), 3 + 3\(\sqrt{2}\), ….
6. 0.2, 0.22, 0.222, 0.2222, ……..
7. 0, -4, -8, -12, ……..
8. \(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \cdots\)
9. 1, 3, 9, 27, ……
10. a, 2a, 3a, 4a, …….
11. a, a², a³, a⁴, …….
12. \(\sqrt{2}\), \(\sqrt{8}\), \(\sqrt{18}\), \(\sqrt{32}\), ……
13. \(\sqrt{3}\), \(\sqrt{6}\), \(\sqrt{9}\), \(\sqrt{12}\), …..
14. 1², 3², 5², 7², …….
15. 1², 5², 7², 7², …….
Solution:
2, 4, 8, 16, ….
a₂ – a₁ = 4 – 2 = 2,
a₃ – a₂ = 8 – 4 = 4,
a₄ – a₃ = 16 – 8 = 8
Here, a₂ – a₁ ≠ a₃ – a₂
Hence, the given list of numbers does not form an AP.

2. 2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), …
a₂ – a₁ = \(\frac{5}{2}-2=\frac{1}{2}\)
a₃ – a₂ = \(3-\frac{5}{2}=\frac{1}{2}\)
a₄ – a₃ = \(\frac{7}{2}-3=\frac{1}{2}\)
Here, a_k+1 – a_k is the same everywhere.
So, the given list of numbers forms an AP with d = \(\frac{1}{2}\)
Next three terms are given by-
a₅ = \(\frac{7}{2}+\frac{1}{2}=4\),
a₆ = \(4+\frac{1}{2}=\frac{9}{2}\) and
a₇ = \(\frac{9}{2}+\frac{1}{2}=5\)

3. -1.2, -3.2, -5.2, -7.2, …..
a₂ – a₁ = -3.2 – (-1.2) = -2
a₃ – a₂ = -5.2 – (-3.2) = -2
a₄ – a₃ = -7.2 – (-5.2) = -2
Here, a_k+1 – a_k is the same everywhere. So, the given list of numbers forms an AP with d = -2.
Next three terms are given by-
a₅ = -7.2 + (-2) = -9.2.
a₆ = -9.2 + (-2) = -11.2 and
a₇ = -11.2 + (-2) = -13.2

4. -10, -6, -2, 2, ……..
a₂ – a₁ = (-6) – (-10) = 4.
a₃ – a₂ = (-2) – (-6) = 4.
a₄ – a₃ = 2 – (-2) = 4
Here, a_k+1 – a_k is the same everywhere.
So, the given list of numbers forms an AP with d = 4.
Next three terms are given by-
a₅ = 2 + 4 = 6,
a₆ = 6 + 4 = 10 and
a₇ = 10 + 4 = 14

5. 3, 3+\(\sqrt{2}\), 3 + 2\(\sqrt{2}\), 3 + 3\(\sqrt{2}\), …
a₂ – a₁ = 3 + \(\sqrt{2}\) – 3 = \(\sqrt{2}\),
a₃ – a₂ = (3 + 2\(\sqrt{2}\)) – (3 + \(\sqrt{2}\)) = \(\sqrt{2}\)
a₄ – a₃ = (3 + 3\(\sqrt{2}\)) – (3 + 2\(\sqrt{2}\)) = \(\sqrt{2}\)
Here, a_k+1 – a_k is the same everywhere.
So, the given list of numbers forms an AP with d = \(\sqrt{2}\).
Next three terms are given by-
a₅ = (3 + 3\(\sqrt{2}\)) + \(\sqrt{2}\) = 3 + 4\(\sqrt{2}\),
a₆ = (3 + 4\(\sqrt{2}\)) + \(\sqrt{2}\) = 3 + 5\(\sqrt{2}\) and
a₇ = (3 + 5\(\sqrt{2}\)) + \(\sqrt{2}\) = 3 + 6\(\sqrt{2}\)

6. 0.2, 0.22, 0.222. 0.2222,…
a₂ – a₁ = 0.22 – 0.2 = 0.02,
a₃ – a₂ = 0.222 – 0.22 = 0.002
Here, a₂ – a₁ ≠ a₃ – a₂.
Hence, the given list of numbers does not form an AP.

7. 0, -4, -8, -12, ….
a₂ – a₁ = (-4) – 0 = -4,
a₃ – a₂ = (-8) – (-4) = -4,
a₄ – a₃ = (-12) – (-8) = -4
Here, a_k+1 – a_k is the same everywhere.
Hence, the given list of numbers forms an AP with d = -4.
Next three terms are given by-
a₅ = (-12) + (-4) = -16,
a₆ = (-16) + (-4) = -20 and
a₇ = (-20) + (-4) = -24.

8.

Here, a_k+1 – a_k is the same everywhere. Hence, the given list of numbers forms an AP with d = 0.
Next three terms are given by-

9. 1, 3, 9, 27, ….
a₂ – a₁ = 3 – 1 = 2,
a₃ – a₂ = 9 – 3 = 6
Here, a₂ – a₁ ≠ a₃ – a₂
Hence, the given list of numbers does not form an AP.

10. a, 2a, 3a, 4a…
a₂ – a₁ = 2a – a = a,
a₃ – a₂ = 3a – 2a = a.
a₄ – a₃ = 4a – 3a = a
Here, a_k+1 – a_k is the same everywhere.
Hence, the given list of unknown numbers forms an AP with d = a.
Next three terms are given by-
a₅ = 4a + a = 5a,
a₆ = 5a + a = 6a and
a₇ = 6a + a = 7a

11. a, a², a³, a⁴,….
a₂ – a₁ = a² – a = a (a – 1),
a₃ – a₂ = a³ – a² = a² (a – 1)
Here, a₂ – a₁ ≠ a₃ – a₂.
Hence, the given list of unknown numbers does not form an AP.

12. \(\sqrt{2}\), \(\sqrt{8}\), \(\sqrt{18}\), \(\sqrt{32}\), ….
We know, \(\sqrt{8}\) = \(\sqrt{4 \times 2}\) = 2\(\sqrt{2}\).
\(\sqrt{18}\) = \(\sqrt{9 \times 2}\) = 3\(\sqrt{2}\) and
\(\sqrt{32}\) = \(\sqrt{16 \times 2}\) = 4\(\sqrt{2}\).
Hence, the given list of numbers is
\(\sqrt{2}\), 2\(\sqrt{2}\), 3\(\sqrt{2}\), 4\(\sqrt{2}\), ….
a₂ – a₁ = 2\(\sqrt{2}\) – \(\sqrt{2}\) = \(\sqrt{2}\),
a₃ – a₂= 3\(\sqrt{2}\) – 2\(\sqrt{2}\) = \(\sqrt{2}\)
a₄ – a₃ = 4\(\sqrt{2}\) – 3\(\sqrt{2}\) = \(\sqrt{2}\)
Here, a_k+1 – a_k is the same everywhere.
Hence, the given list of numbers forms an AP with d = \(\sqrt{2}\).
Next three terms are given by-
a₅ = 4\(\sqrt{2}\) + \(\sqrt{2}\) = 5\(\sqrt{2}\) = \(\sqrt{50}\).
a₆ = 5\(\sqrt{2}\) + \(\sqrt{2}\) = 6\(\sqrt{2}\) = \(\sqrt{72}\) and
a₇ = 6\(\sqrt{2}\) + \(\sqrt{2}\) = 7\(\sqrt{2}\) = \(\sqrt{98}\).

13. \(\sqrt{3}\), \(\sqrt{6}\), \(\sqrt{9}\), \(\sqrt{12}\), ……
a₂ – a₁ = \(\sqrt{6}\) – \(\sqrt{3}\) = \(\sqrt{3}\)(\(\sqrt{2}\) – 1)
a₃ – a₂ = \(\sqrt{9}\) – \(\sqrt{6}\) = \(\sqrt{3}\)(\(\sqrt{3}-\sqrt{2}\))
Here, a₂ – a₁ ≠ a₃ – a₂
Hence, the given list of numbers does not form an AP.

14. 1², 3², 5², 7², ….
a₂ – a₁ = 3² – 1² = 9 – 1 = 8,
a₃ – a₂ = 5² – 3² = 25 – 9 = 16
Here, a₂ – a₁ ≠ a₃ – a₂
Hence, the given list of numbers does not form an AP.

15. 1², 5², 7², 7²,…
a₂ – a₁ = 5² – 1² = 25 – 1 = 24,
a₃ – a₂ = 7² – 5² = 49 – 25 = 24,
a₄ – a₃ = 73 – 7² = 73 – 49 = 24.
Here. a_k+1 – a_k is the same everywhere.
Hence, the given list of numbers forms an AP with d = 24.
Next three terms are given by-
a₅ = 73 + 24 = 97,
a₆ = 97 + 24 = 121 and
a₇ = 121 + 24 = 145.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 Quadratic Equations Ex 4.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 Quadratic Equations Exercise 4.1

Question 1.
Check whether the following are quadratic equations:
1. (x + 1)² = 2(x – 3)
2. x² – 2x = (-2)(3 – x)
3. (x – 2)(x + 1) = (x – 1)(x + 3)
4. (x – 3)(2x + 1) = x(x + 5)
5. (2x – 1)(x – 3) = (x + 5)(x – 1)
6. x² + 3x + 1 = (x – 2)²
7. (x + 2) = 2x(x² – 1)
8. x³ – 4x² – x + 1 = (x – 2)³
Solution:
1. Here, LHS = (x + 1)² = x² + 2x + 1 and
RHS = 2(x – 3) = 2x – 6.
Hence, (x + 1)² = 2(x – 3) can be rewritten as x² + 2x + 1 = 2x – 6
∴ x² + 2x + 1 – 2x + 6 = 0
∴ x² + 7 = 0
It is of the form ax² + bx + c = 0.
(a = 1, b = 0, c = 7)
Hence, the given equation is a quadratic equation.

2. Here, RHS = (-2)(3 – x) = -6 + 2x.
Hence, x² – 2x = (-2) (3 – x) can be rewritten as
x² – 2x = -6 + 2x
∴ x² – 4x + 6 = 0
It is of the form ax² + bx + c = 0.
(a = 1, b = -4, c = 6)
Hence, the given equation is a quadratic equation.

3. Here, LHS = (x – 2) (x + 1) = x² – x – 2 and
RHS = (x – 1)(x + 3) = x² + 2x – 3.
Hence, (x – 2)(x + 1)(x – 1)(x + 3) be rewritten as
x² – x – 2 = x² + 2x – 3
∴ -3x + 1 = 0
It is not of the form ax² + bx + c = 0.
Hence, the given equation is not a quadratic equation.

4. Here, LHS = (x – 3) (2x + 1) = 2x² – 5x – 3
and RHS = x(x + 5) = x² + 5x.
Hence, (x – 3) (2x + 1) = x(x + 5) can be rewritten as
2x² – 5x – 3 = x² + 5x
∴ x² – 10x – 3 = 0
It is of the form ax² + bx + c = 0.
(a = 1, b = -10, c = -3)
Hence, the given equation is a quadratic equation.

5. Here, LHS = (2x – 1)(x – 3) = 2x² – 7x + 3 and
RHS = (x + 5) (x – 1) = x² + 4x – 5.
Hence, the given equation can be rewritten as
2x² – 7x + 3 = x² + 4x – 5
∴ x² – 11x + 8 = 0
It is of the form ax2 + bx + c = 0.
(a = 1, b = -11, c = 8)
Hence, the given equation is a quadratic equation.

6. Here, RHS = (x – 2)² = x² – 4x + 4
Hence, the given equation can be rewritten as
x² + 3x + 1 = x² – 4x + 4
∴ 7x – 3 = 0
It is not of the form ax² + bx + c = 0.
Hence, the given equation is not a quadratic equation.

7. Here, LHS = (x + 2)³ = x³ + 6x² + 12x + 8 and
RHS = 2x (x² – 1) = 2x³ – 2x.
Hence, the given equation can be rewritten as
x³ + 6x² + 12x + 8 = 2x³ – 2x
∴ -x³ + 6x² + 14x + 8 = 0
It is not of the form ax² + bx + c = 0.
Hence, the given equation is not a quadratic equation.

8. Here, RHS = (x – 2)³ = x³ – 6x² + 12x – 8.
Hence, the given equation can be rewritten as
x³ – 4x² – x + 1 = x³ – 6x² + 12x – 8
2x² – 13x + 9 = 0
It is of the form ax² + bx + c = 0.
(a = 2, b = -13, c = 9)
Hence, the given equation is a quadratic equation.

Question 2.
Represent the following situations in the form of quadratic equations:
1. The area of a rectangular plot is 528 m². The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.
Solution:
Let the breadth (in metres) of the rectangular plot be x.
Then, the length (in metres) of the rectangular plot is 2x + 1.
Area of the rectangular plot = Length × Breadth
∴ 528 = (2x + 1) × x
(∵ Area is given to be 528 m²)
∴ 528 = 2x² + x
∴ 2x² + x – 528 = 0 is the required quadratic equation to find the length (2x + 1 m) and breadth (x m) of the rectangular plot.

2. The product of two consecutive positive integers is 306. We need to find the integers.
Solution:
Let the two consecutive positive integer be x and x + 1.
Then, their product = x(x + 1) = x² + x.
This product is given to be 306.
∴ x² + x = 306
∴ x² + x – 306 = 0 is the required quadratic equation to find the consecutive positive integers x and x + 1.

3. Rohan’s mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find Rohan’s present age.
Solution:
Let Rohan’s present age (in years) be x.
Then, his mother’s present age (in years) = x + 26.
3 years from now, Rohan’s age (in years) will be x + 3 and his mother’s age (in years) will be x + 29.
The product of their ages (in years) 3 years from now is given to be 360.
Hence, (x + 3)(x + 29) = 360
∴ x² + 32x + 87 – 360 = 0
∴ x² + 32x – 273 = 0 is the required quadratic equation to find the present ages (in years) of Rohan (x) and his mother (x + 26).

4. A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
Solution:
Let the usual uniform speed of the train be x km/h.
Now, Time = \(\frac{\text { distance }}{\text { speed }}\)
∴ Time required to cover 480 km distance at usual speed = t₁ = \(\frac{480}{x}\) hours
If the speed is 8 km/hour less, the new speed would be (x – 8) km/hour.
∴ Time required to cover 480 km distance at new speed = t₂ = \(\frac{480}{x-8}\) hours
Now, the time required at new speed is 3 hours more than the usual time.
∴ t₂ = t₁ + 3
∴ \(\frac{480}{x-8}=\frac{480}{x}+3\)
∴ 480x = 480(x – 8) + 3x(x – 8)
(Multiplying by x(x – 8))
∴ 480x = 480x – 3840 + 3x² – 24x
∴ 0 = 3x² – 24x – 3840
∴ x² – 8x – 1280 = 0 is the required quadratic equation to find the usual speed (x km/h) of the train.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 Quadratic Equations Ex 4.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 Quadratic Equations Exercise 4.4

Question 1.
Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:
1. 2x² – 3x + 5 = 0
2. 3x² – 4\(\sqrt{3}\)x + 4 = 0
3. 2x² – 6x + 3 = 0
Solution:
The given equation is of the form
ax² + bx + c = 0; where a = 2, b = -3 and c = 5.
Then, the discriminant
b² – 4ac = (-3)² – 4(2)(5)
= 9 – 40
= -31 <0
So, the given equation has no real roots.

2. Comparing the given equation with the standard quadratic equation
ax² + bx + c = 0, we get a = 3, b = -4\(\sqrt{3}\) and c = 4.
Then, the discriminant
b² – 4ac = (-4\(\sqrt{3}\))² – 4(3)(4)
= 48 – 48
= 0
So, the given equation has equal real roots.
The roots are \(-\frac{b}{2 a},-\frac{b}{2 a}\)
i.e., \(-\frac{-4 \sqrt{3}}{2(3)},-\frac{-4 \sqrt{3}}{2(3)}\), i.e., \(\frac{2}{\sqrt{3}}, \frac{2}{\sqrt{3}}\)

3. The given equation is of the form
ax² + bx + c = 0, where a = 2, b = -6 and c = 3.
Then, the discriminant
b² – 4ac = (-6)² – 4(2)(3)
= 36 – 24
= 12
So, the given equation has two distinct roots.
The roots are given by
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
\(=\frac{6 \pm \sqrt{12}}{2(2)}\)
\(=\frac{6 \pm 2 \sqrt{3}}{4}=\frac{3 \pm \sqrt{3}}{2}\)
Thus, the roots of the given equation are \(\frac{3+\sqrt{3}}{2}\) and \(\frac{3-\sqrt{3}}{2}\)

Question 2.
Find the values of k for each of the following quadratic equations, so that they have two equal roots:
1. 2x² + kx + 3 = 0
2. kx (x – 2) + 6 = 0
Solution:
1. Comparing the given equation with the standard quadratic equation, we have
a = 2, b = k and c = 3.
Then, the discriminant = b² – 4ac
= (k)² – 4 (2) (3)
= k² – 24
If the equation has two equal roots, then the discriminant = 0
∴ k² – 24 = 0
∴ k² = 24
∴ k = ±\(\sqrt{24}\)
∴ k ± 2\(\sqrt{6}\)

2. kx(x – 2) + 6 = 0
∴ kx² – 2kx + 6 = 0
Here, a = k, b = -2k and c = 6.
Then, the discriminant = b² – 4ac
= (-2k)² – 4(k)(6)
= 4k² – 24k
If the equation has two equal roots, then the discriminant = 0
∴ 4k² – 24k = 0
∴ 4k (k – 6) = 0
∴ k = 0 or k = 6
But k = 0 is not possible because if k = 0, the equation reduces to 6 = 0, not a quadratic equation.
∴ k = 6

Question 3.
Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m²? If so, find its length and breadth.
Solution:
Considering that the required mango grove can be designed, let the breadth of the mango grove be x m.
Then, the length of the mango grove is 2x m. Area of rectangular mango grove
= Length × Breadth
= 2x × x
= 2x² m²
The required area is 800 m².
∴ 2x² = 800
∴ 2x² – 800 = 0
∴ x² – 400 = 0
If the above equation has real roots, then it is possible to design the required mango grove.
Here, a = 1, b = 0 and c = -400.
Then, the discriminant = b² – 4ac
= (0)² – 4(1)(-400)
= 1600 > 0
Hence, the equation has real roots. So, it is possible to design the mango grove with required measures.
Now, x² – 400 = 0
∴ (x + 20) (x – 20) = 0
∴ x + 20 = 0 or x – 20 = 0
∴ x = -20 or x = 20
Since x is the breadth of the rectangular mango grove, x = -20 is not possible.
∴ x = 20 and 2x = 40
Thus, the length of the mango grove is 40 m and its breadth is 20 m.

Question 4.
Is the following situation possible? If so, determine their present ages.
The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Solution:
Let the present ages of two friends be x years and (20 – x) years.
Four years ago, their respective ages were (x – 4) years and (20 – x – 4) years, i.e., (16 – x) years.
Then, according to given,
(x – 4) (16 – x) = 48
∴ 16x – x² – 64 + 4x = 48
∴ -x² + 20x – 64 – 48 = 0
∴ -x² + 20x – 112 = 0
∴ x² – 20x + 112 = 0
Here, a = 1, b = -20 and c = 112.
Then, the discriminant
b² – 4ac = (-20)² – 4(1)(112)
= 400 – 448
= -48 < 0
Hence, the equation has no real roots. So, the given situation is not possible.

Question 5.
Is it possible to design a rectangular park of perimeter 80 m and area 400 m² ? If so, find its length and breadth.
Solution:
Let the length of the rectangular park be x m.
Perimeter of rectangular park = 2 (Length + Breadth)
∴ 80 = 2(x + Breadth)
∴ 40 = x + Breadth
∴ Breadth = (40 – x) m
Now, area of rectangular park = Length × Breadth
∴ 400 = x (40 – x)
∴ 400 = 40x – x²
∴ x² – 40x + 400 = 0
Here, a = 1, b = -40 and c = 400.
Then, the discriminant = b² – 4ac
= (-40)² – 4(1)(400)
= 1600 – 1600
= 0
Hence, the equation has equal real roots. So, it is possible to design a rectangular park with given measures.
x² – 40x + 400 = 0
∴ x² – 20x – 20x + 400 = 0
∴ x(x – 20) – 20(x – 20) = 0
∴ (x – 20) (x – 20) = 0
∴ x – 20 = 0 or x – 20 = 0
∴ x = 20 or x = 20
Thus, the length of the rectangular park = x = 20 m and the breadth of the rectangular park = 40 – x = 40 – 20 = 20 m.
Note: Here the shape of the park turns out to be a square, but as we know, every square is a rectangle.