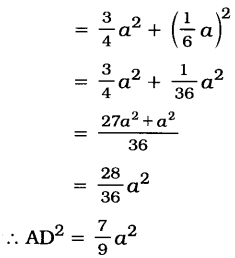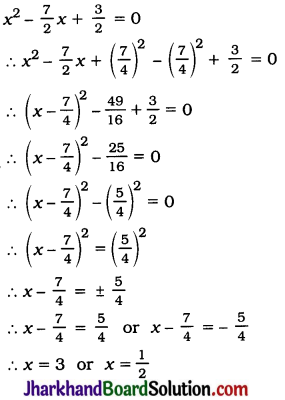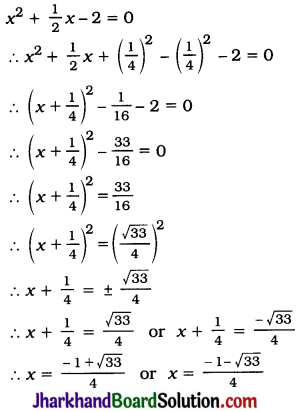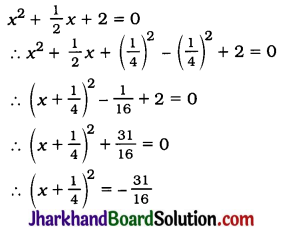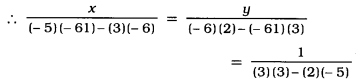Month: April 2023

Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 Triangles Ex 6.6 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 6 Triangles Exercise 6.6

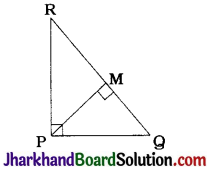
Question 1.
In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that \(\frac{QS}{SR}=\frac{PQ}{PR}\)
Solution :

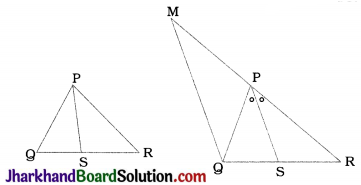
Construction: Through Q, draw a line parallel to PS which intersects RP extended at M.
Proof: In ΔMQR, S and P are points on QR and MR respectively and PS || MQ.
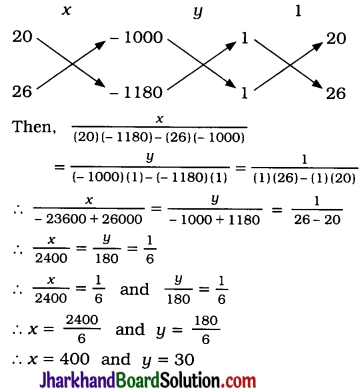
∴ \(\frac{QS}{SR}=\frac{MP}{PR}\) (BPT) ……………(1)
Now, PS || MQ and PQ is their transversal.
∴ ∠SPQ = ∠PQM (Alternate angles) ……(2)
Similarly, PS || MQ and MR is their transversal.
∴ ∠RPS = ∠PMQ (Corresponding angles) …………….(3)
PS is the bisector of ∠QPR.
∴ ∠SPQ = ∠RPS …………….(4)
From (2), (3) and (4).
∠PQM = ∠PMQ.
∴ In ΔPMQ, MP = PQ ……….(5)
From (1) and (5), we get
\(\frac{QS}{SR}=\frac{PQ}{PR}\)

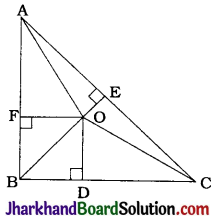
Question 2.
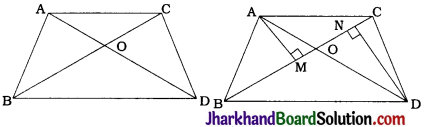
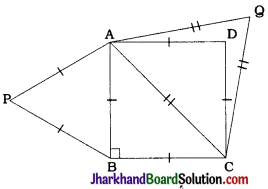
In the given figure, D is a point on hypotenuse AC of ΔABC, such that BD ⊥ AC, DM ⊥ BC and DN ⊥ AB. Prove that:
1. DM² = DN . MC
2. DN² = DM . AN
Solution :

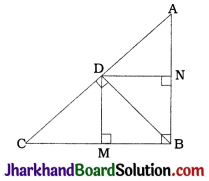
In quadrilateral DMBN, ∠B = ∠M = ∠N = 90°.
Hence, DMBN is a rectangle.
∴ DN = MB ………….. (1)
and DM = NB ………….. (2)
Now, BD ⊥ AC
∴ ∠BDC = 90° and ΔBDC is a right triangle in which DM is altitude on hypotenuse BC.
Then, ΔBMD ~ ΔDMC ~ ΔBDC. (Theorem 6.7)
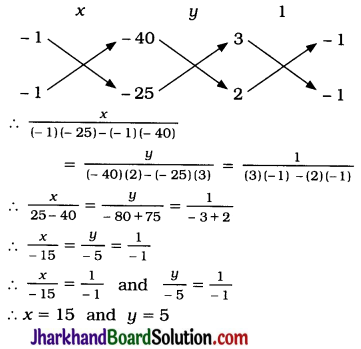
∴ \(\frac{DM}{CM}=\frac{BM}{DM}\)
∴ DM² = BM. CM
∴ DM² = DN. MC [By (1), DN = MB] [Result (1)]
Similarly, ΔADB is a right triangle in which DN is altitude on hypotenuse AB.
∴ ΔAND ~ ΔDNB ~ ΔADB (Theorem 6.7)
∴ \(\frac{DN}{BN}=\frac{AN}{DN}\)
∴ DN2 = BN. AN
∴ DN² = DM . AN [By (2), DM = NB] [Result (2)]

Question 3.
In the given figure, ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that AC² = AB² + BC² + 2BC . BD.
Solution :

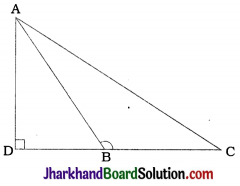
In ΔADC, ∠D = 90°
∴ AC² = AD² + DC²
∴ AD² = AC² – DC² ……………(1)
In ΔADB, ∠D = 90°
∴ AB² = AD² + DB²
∴ AD² = AB² – DB² ……………(2)
From (1) and (2).
AC² – DC² = AB² – DB²
∴ AC² = AB² + DC² – DB²
∴ AC² = AB2 + (BC + DB)² – DB²
∴ AC² = AB² + BC² + 2BC . DB + DB² – DB²
∴ AC² = AB² + BC² + 2BC . BD

Question 4.
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC² = AB² + BC² – 2BC . BD.
Solution :

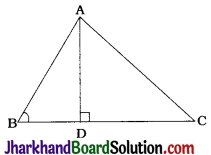
In ΔADC, ∠D = 90°
∴ AC² = AD² + CD²
∴ AD² = AC² – CD² ……………….(1)
In ΔADB, ∠D = 90°
∴ AB² = AD² + BD²
∴ AD² = AB² – BD² ……………….(2)
From (1) and (2),
AC² – CD² = AB² -BD²
∴ AC² = AB² + CD² – BD²
∴ AC² = AB² + (BC – BD)² – BD²
∴ AC² = AB² + BC² – 2BC . BD + BD² – BD²
∴ AC² = AB² + BC² – 2BC . BD

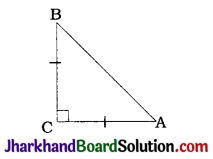
Question 5.
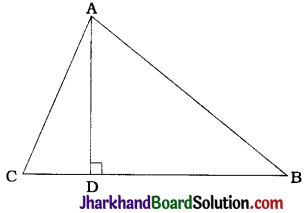
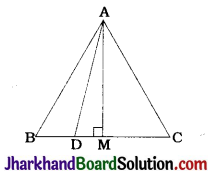
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:
1. AC² = AD² + BC. DM + (\(\frac{BC}{2}\))²
2. AB² = AD² – BC. DM + (\(\frac{BC}{2}\))²
3. AC² + AB² = 2AD² + \(\frac{1}{2}\)BC²
Solution :

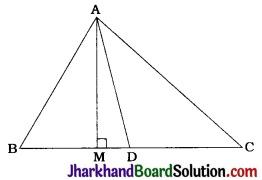
Here, ΔAMD, ΔAMC and ΔAMB are right triangles.
Also, since AD is a median, D is the midpoint of BC.
∴ CD = BD = \(\frac{BC}{2}\)
Moreover, DM = CM – CD and DM = BD – BM
1. In ΔAMC, ∠M = 90°
∴ AC² = AM² + CM²
∴ AC² = AM² + (DM + CD)²
∴ AC² = AM² + DM² + 2. DM.CD + CD²
∴ AC² = (AM² + DM²) + (2CD) (DM) + CD²
∴ AC² = AD² + BC.DM + (\(\frac{BC}{2}\))²
(∵ In ΔAMD, AD² = AM² + DM²)

2. In ΔAMB, ∠M = 90°
∴ AB² = AM² + BM²
∴ AB² = AM² + (BD – DM)²
∴ AB² = AM² + BD² – 2 BD.DM + DM²
∴ AB² = (AM² + DM²) – (2BD) · (DM) + BD²
∴ AB² = AD² – BC.DM + (\(\frac{BC}{2}\))²
(∵ In ΔAMD, AD² = AM² + DM²)

3. Now, adding the results of part (1) and (2)
AC² + AB² = AD² + BC. DM + (\(\frac{BC}{2}\))² + AD² – BC . DM + (\(\frac{BC}{2}\))²
∴ AC² + AB² = 2AD² + 2(\(\frac{\mathrm{BC}^2}{4}\))
∴ AC² + AB² = 2AD² + \(\frac{1}{2}\)BC²
[Note: In this result, if we replace BC by 2BD, we get the famous result know as Apollonius theorem : If AD is a median of ΔABC, then AB² + AC² = 2 (AD² + BD²).]

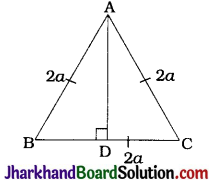
Question 6.
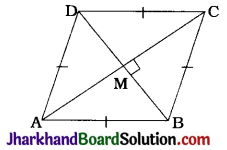
Prove that the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.
Solution :
First of all, we prove Apollonius Theorem.
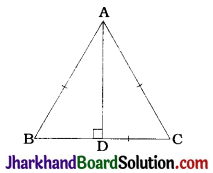
In ΔABC, let AD be a median and AM be an altitude as shown in the figure.
Then, AB² + AC²
= AM² + BM² + AM² + CM²
= 2AM² + (BD – MD)² + (CD + MD)²
= 2AM² + (BD – MD)² + (BD + MD)² (∵ CD = BD)
= 2AM² + 2BD² + 2MD²
= 2(AM² + MD²) + 2BD²
= 2AD² + 2BD²
∴ AB² + AC² = 2(AD² + BD²)

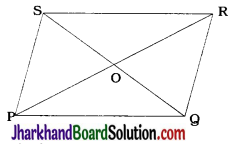
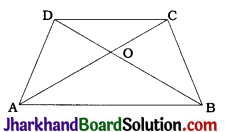
Let PQRS be a parallelogram in which the diagonals bisect each other at O.
Then, PO = RO = \(\frac{1}{2}\)PR and
QO = SO = \(\frac{1}{2}\)QS.
Now, in ΔPQR, QO is a median.
∴ PQ² + QR² = 2(QO² + PO²)
∴ PQ² + QR² = 2{(\(\frac{QS}{2}\))² + (\(\frac{PR}{2}\))²}
∴ PQ² + QR² = \(\frac{1}{2}\)(QS² + PR² ) ………….(1)
Similarly.
in ΔQRS, QR² + RS² = \(\frac{1}{2}\)(QR² + PR²) ……(2)
in ΔRSP, RS² + SP² = \(\frac{1}{2}\)(QS² + PR²) ……….(3)
in ΔSPQ, SP² + PQ² = \(\frac{1}{2}\)(QS² + PR²) ……….(4)
Adding (1), (2), (3) and (4), we get
2(PQ² + QR² + RS² + SP²) = 2(QS² + PR²)
∴ PQ² + QR² + RS² + SP² = QS² + PR²
Thus, the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.

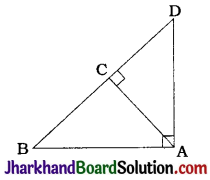
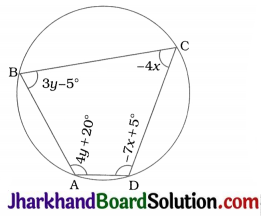
Question 7.
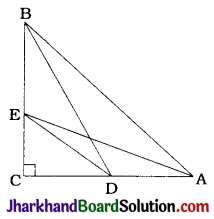
In the given figure, two chords AB and CD intersect each other at the point P. Prove that
1. ΔAPC ~ ΔDPB
2. AP . PB = CP . DP
Solution :

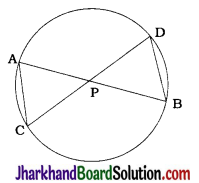
Here, ∠CAB = ∠CDB
(Angles in the same segment)
∴ ∠CAP = ∠BDP
Similarly,
∠ACD = ∠DBA
(Angles in the same segment)
∴ ∠ACP = ∠DBP
Now, in ΔAPC and ΔDPB,
∠CAP = ∠BDP and ∠ACP = ∠DBP.
∴ By AA criterion, ΔAPC ~ ΔDPB. (Result 1)
∴ \(\frac{AP}{DP}=\frac{CP}{BP}\)
∴ AP . PB = CP . DP (Result 2)

Question 8.
In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle.
Prove that
1. ΔPAC ~ ΔPDB
2. PA . PB = PC . PD
Solution :

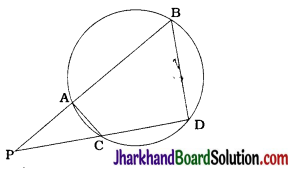
In cyclic quadrilateral ACDB,
ΔACD + ∠ABD = 180°
Again, ∠ACD + ∠ACP = 180° (Linear pair)
∴ ∠ABD = ∠ACP
∴ ∠PBD = ∠PCA.
Similarly, ∠CAB + ∠CDB = 180° (Cyclic quadrilateral)
∠CAB + ∠CAP = 180° (Linear pair)
∴ ∠CDB = ∠CAP
∴ ∠PDB = ∠PAC
Now, in ΔPDB and ΔPAC,
∠PBD = ∠PCA
∠PDB = ∠PAC
∴ By AA criterion, ΔPAC ~ ΔPDB [Result (1)]
∴ \(\frac{PA}{PD}=\frac{PC}{PB}\)
∴ PA.PB = PC.PD [Result (2)]

Question 9.
In the given figure, D is a point on side BC of ΔABC such that \(\frac{BD}{CD}=\frac{AB}{AC}\). Prove that AD is the bisector of ∠BAC.
Solution :

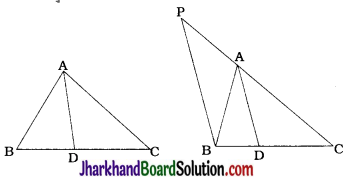
Through B. draw a line parallel to AD to intersect CA extended at P.
Then, in ΔPBC, A and D are points on PC and BC respectively and PB || AD.
∴ \(\frac{PA}{AC}=\frac{BD}{CD}\)
Also, \(\frac{BD}{CD}=\frac{AB}{AC}\) (Given)
∴ PA = AB
Now, in ΔPAB, PA = AB
∴ ∠ABP = ∠APB …………..(1)
AD || BP and AB is their transversal.
∴ ∠ABP = ∠BAD (Alternate angles) …………..(2)
AD || BP and CP is their transversal.
∴ ∠APB = ∠CAD (Corresponding angles) …………..(3)
From (1), (2) and (3),
∠BAD = ∠CAD
Moreover, ∠BAD + ∠CAD = ∠BAC.
Hence, AD is the bisector of ∠BAC.

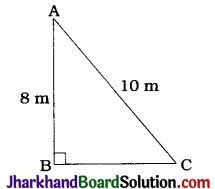
Question 10.
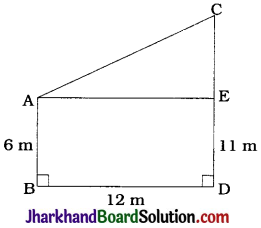
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away from her and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see the given figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?
Solution :

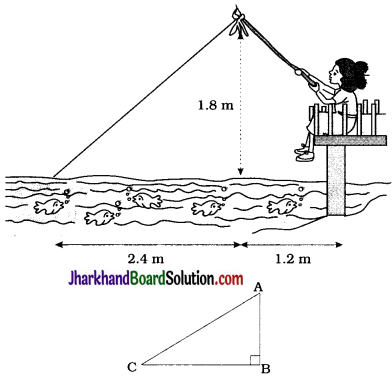
Here, ΔABC represents the initial position in which A is the tip of her fishing rod, C is the fly at the end of the string and B is the point directly under the tip of the rod.
Then, in ΔABC, ∠B = 90°, AB = 1.8m and BC = 2.4 m.
∴ AC² = AB² + BC² (Pythagoras theorem)
∴ AC² = (1.8)² + (2.4)²
∴ AC² = 3.24 + 5.76
∴ AC² = 9
∴ AC = 3 m
Hence, in the initial position, she has 3 m of string out.
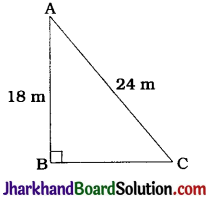
Length of string pulled-in in 1 sec = 5 cm
∴ Length of string pulled-in in 12 sec = 60 cm = 0.6 m
Now, in the second position, the length of string AC = 3m-0.6 m = 2.4 m and AB = 1.8 m.
Again, AC² = AB² + BC²
∴ (2.4)² = (1.8)² + BC²
∴ BC² = (2.4)² – (1.8)²
∴ BC² = (2.4 + 1.8) (2.4 – 1.8)
∴ BC² = 4.2 × 0.6
∴ BC² = 2.52
∴ BC = \(\sqrt{2.52}\)
∴ BC= 1.59 m (approx)
Now, the horizontal distance of the fly from her
= BC + 1.2 m
= (1.59 + 1.2) m
= 2.79 m

Jharkhand Board JAC Class 10 Maths Solutions Chapter 5 Arithmetic Progressions Ex 5.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 5 Arithmetic Progressions Exercise 5.1

Question 1.
In which of the following situations, does the list of numbers involved make an arithmetic progression, and why?
1. The taxi fare after each km, when the fare is ₹ 15 for the first km and ₹ 8 for each additional km.
2. The amount of air present in a cylinder when a vacuum pump removes \(\frac{1}{4}\) of the air remaining in the cylinder at a time.
3. The cost of digging a well after every metre of digging, when it costs ₹ 150 for the first metre and rises by ₹ 50 for each subsequent metre.
4. The amount of money in the account every year, when ₹ 10,000 is deposited at compound interest at 8% per annum.
Solution:
1. Here, the fare for 1 km = ₹ 15
the fare for 2 km = ₹ 15 + ₹ 8 = ₹ 23,
the fare for 3 km = ₹ 15 + 2 (₹8) = ₹ 31,
the fare for 4 km = ₹ 15 + 3 (₹8) = ₹ 39, and so on.
The list of numbers formed is 15, 23, 31, 39, …………..
Here, a₂ – a₁ = 23 – 15 = 8.
a₃ – a₂ = 31 – 23 = 8.
a₄ – a₃ = 39 – 31 = 8, and so on.
Thus, a_k+1 – a_k is the same every time.
Hence, the list of numbers forms an AP with a = 15 and d = 8.

2. Let the volume of air present in the cylinder at the beginning be V units. Then, volume of air remaining in the cylinder after first attempt = \(\frac{3}{4}\)V units. Also, volume of air remaining in the cylinder after second attempt = \(\left(\frac{3}{4}\right)^2\)V units. Here, the list of numbers formed is V, \(\frac{3}{4}\)V, \(\left(\frac{3}{4}\right)^2\)V, ………
Now, a₂ – a₁ = \(\frac{3}{4}\)V – V = –\(\frac{1}{4}\)V
a₃ – a₂ = \(\left(\frac{3}{4}\right)^2\)V – \(\frac{3}{4}\)V
= \(V\left(\frac{9}{16}-\frac{3}{4}\right)\)
= \(– \frac{3}{16}\)V
Here, a₂ – a₁ ≠ a₃ – a₂.
Hence, the list of numbers does not form an AP.

3. Cost of digging first metre = ₹ 150
Cost of digging the second metre = ₹ 150 + ₹ 50
= ₹ 200
Cost of digging the third metre = ₹ 200 + ₹ 50
= ₹ 250
Cost of digging the fourth metre = ₹ 250 + ₹ 50
= ₹ 300
The list of numbers formed is 150, 200, 250, 300,…
Here, a₂ – a₁ = 200 – 150 = 50,
a₃ – a₂ = 250 – 200 = 50,
a₄ – a₃ = 300 – 250 = 50, and so on.
Thus, a_k+1 – a_k is the same every time. Hence, the list of numbers forms an AP with a = 150 and d = 50.

4. The formula of compound interest is known to us.
A = \(P\left(1+\frac{R}{100}\right)^T\)
Here, P = ₹ 10,000; R = 8% and T = 1, 2, 3, 4, ……….
Amount at the end of 1st year = ₹ 10000 (1.08).
Amount at the end of 2nd year = ₹ 10000 (1.08)².
Amount at the end of 3rd year = ₹ 10000 (1.08)³.
The list of numbers formed is 10000 (1.08), 10000 (1.08)2, 10000 (1.08), ………..
a₂ – a₁ = 10000 (1.08)² – 10000 (1.08)³
= 10000 (1.08) (1.08 – 1)
= 10000 (1.08) (0.08)
a₃ – a₂ = 10000 (1.08)³ – 10000 (1.08)²
= 10000 (1.08)² (1.08 – 1)
= 10000 (1.08)² (0.08)
Thus, a₂ – a₁ ≠ a₃ – a₂
Hence, the list of numbers does not form an AP.

Question 2.
Write first four terms of the AP when the first term a and the common difference d are given as follows:
1. a = 10, d = 10
2. a = -2, d = 0
3. a = 4, d = -3
4. a = -1, d = \(\frac{1}{2}\)
5. a = -1.25, d = -0.25
Solution:
1. a = 10, d = 10
First term a = 10
Second term = First term + d
= 10 + 10 = 20
Third term = Second term + d
= 20 + 10 = 30
Fourth term = Third term + d
= 30 + 10 = 40
Thus, the required first four terms of the AP are 10, 20, 30, 40.

2. a = -2, d = 0
First term = a = -2
Second term = First term + d
= -2 + 0 = -2
Third term = Second term + d
= -2 + 0 = -2
Fourth term = Third term + d
= -2 + 0 = -2
Thus, the required first four terms of the AP are -2, -2, -2, -2.

3. a = 4, d = -3
First term = a = 4
Second term = First term + d
= 4 + (-3) = 1
Third term = Second term + d
= 1 + (-3) = -2
Fourth term = Third term + d
= (-2) + (-3) = -5
Thus, the required first four terms of the AP are 4, 1, -2, -5.

4. a = -1, d = \(\frac{1}{2}\)
First term = a = -1
Second term = First term + d
= -1 + \(\frac{1}{2}\) = –\(\frac{1}{2}\)
Third term = Second term + d
= \(-\frac{1}{2}+\frac{1}{2}\) = 0
Fourth term = Third term + d
= 0 + \(\frac{1}{2}\) = \(\frac{1}{2}\)
Thus, the required first four terms of the AP are -1, – \(\frac{1}{2}\), 0, \(\frac{1}{2}\).

5. a = -1.25, d = -0.25
The general form of an AP is a, a + d, a + 2d, a + 3d, …….. Then,
First term = a = -1.25
Second term = a + d
= -1.25 + (-0.25) = -1.50
Third term = a + 2d
= -1.25 + 2(-0.25) = -1.75
Fourth term = a + 3d
= -1.25 + 3(-0.25) = -2.00
Thus, the required first four terms of the AP are -1.25, -1.50, -1.75, -2.00.

Question 3.
For the following APs, write the first term and the common difference:
1. 3, 1, 1, -3, ……..
2. -5, -1, 3, 7, …….
3. \(\frac{1}{3}, \frac{5}{3}, \frac{9}{3}, \frac{13}{3}, \ldots\)
4. 0.6, 1.7, 2.8, 3.9, …
Solution:
1. 3, 1, -1, -3,….
First term a = 3
Common difference d = a₂ – a₁ = 1 – 3 = -2

2. -5, 1, 3, 7,…..
First term a = -5
Common difference d = (-1) – (-5) = 4

3. \(\frac{1}{3}, \frac{5}{3}, \frac{9}{3}, \frac{13}{3}, \ldots\)
First term a = \(\frac{1}{3}\)
Common difference d = \(\frac{5}{3}-\frac{1}{3}=\frac{4}{3}\)

4. 0.6, 1.7, 2.8, 3.9, ……
First term a = 0.6
Common difference d = 1.7 – 0.6 = 1.1

Question 4.
Which of the following are APs? If they form an AP find the common difference d and write three more terms:
1. 2, 4, 8, 16, …….
2. 2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), …….
3. -1.2, -3.2, -5.2, -7.2, …….
4. -10, -6, -2, 2, …….
5. 3, 3 + 2\(\sqrt{2}\), 3 + 2\(\sqrt{2}\), 3 + 3\(\sqrt{2}\), ….
6. 0.2, 0.22, 0.222, 0.2222, ……..
7. 0, -4, -8, -12, ……..
8. \(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \cdots\)
9. 1, 3, 9, 27, ……
10. a, 2a, 3a, 4a, …….
11. a, a², a³, a⁴, …….
12. \(\sqrt{2}\), \(\sqrt{8}\), \(\sqrt{18}\), \(\sqrt{32}\), ……
13. \(\sqrt{3}\), \(\sqrt{6}\), \(\sqrt{9}\), \(\sqrt{12}\), …..
14. 1², 3², 5², 7², …….
15. 1², 5², 7², 7², …….
Solution:
2, 4, 8, 16, ….
a₂ – a₁ = 4 – 2 = 2,
a₃ – a₂ = 8 – 4 = 4,
a₄ – a₃ = 16 – 8 = 8
Here, a₂ – a₁ ≠ a₃ – a₂
Hence, the given list of numbers does not form an AP.

2. 2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), …
a₂ – a₁ = \(\frac{5}{2}-2=\frac{1}{2}\)
a₃ – a₂ = \(3-\frac{5}{2}=\frac{1}{2}\)
a₄ – a₃ = \(\frac{7}{2}-3=\frac{1}{2}\)
Here, a_k+1 – a_k is the same everywhere.
So, the given list of numbers forms an AP with d = \(\frac{1}{2}\)
Next three terms are given by-
a₅ = \(\frac{7}{2}+\frac{1}{2}=4\),
a₆ = \(4+\frac{1}{2}=\frac{9}{2}\) and
a₇ = \(\frac{9}{2}+\frac{1}{2}=5\)

3. -1.2, -3.2, -5.2, -7.2, …..
a₂ – a₁ = -3.2 – (-1.2) = -2
a₃ – a₂ = -5.2 – (-3.2) = -2
a₄ – a₃ = -7.2 – (-5.2) = -2
Here, a_k+1 – a_k is the same everywhere. So, the given list of numbers forms an AP with d = -2.
Next three terms are given by-
a₅ = -7.2 + (-2) = -9.2.
a₆ = -9.2 + (-2) = -11.2 and
a₇ = -11.2 + (-2) = -13.2

4. -10, -6, -2, 2, ……..
a₂ – a₁ = (-6) – (-10) = 4.
a₃ – a₂ = (-2) – (-6) = 4.
a₄ – a₃ = 2 – (-2) = 4
Here, a_k+1 – a_k is the same everywhere.
So, the given list of numbers forms an AP with d = 4.
Next three terms are given by-
a₅ = 2 + 4 = 6,
a₆ = 6 + 4 = 10 and
a₇ = 10 + 4 = 14

5. 3, 3+\(\sqrt{2}\), 3 + 2\(\sqrt{2}\), 3 + 3\(\sqrt{2}\), …
a₂ – a₁ = 3 + \(\sqrt{2}\) – 3 = \(\sqrt{2}\),
a₃ – a₂ = (3 + 2\(\sqrt{2}\)) – (3 + \(\sqrt{2}\)) = \(\sqrt{2}\)
a₄ – a₃ = (3 + 3\(\sqrt{2}\)) – (3 + 2\(\sqrt{2}\)) = \(\sqrt{2}\)
Here, a_k+1 – a_k is the same everywhere.
So, the given list of numbers forms an AP with d = \(\sqrt{2}\).
Next three terms are given by-
a₅ = (3 + 3\(\sqrt{2}\)) + \(\sqrt{2}\) = 3 + 4\(\sqrt{2}\),
a₆ = (3 + 4\(\sqrt{2}\)) + \(\sqrt{2}\) = 3 + 5\(\sqrt{2}\) and
a₇ = (3 + 5\(\sqrt{2}\)) + \(\sqrt{2}\) = 3 + 6\(\sqrt{2}\)

6. 0.2, 0.22, 0.222. 0.2222,…
a₂ – a₁ = 0.22 – 0.2 = 0.02,
a₃ – a₂ = 0.222 – 0.22 = 0.002
Here, a₂ – a₁ ≠ a₃ – a₂.
Hence, the given list of numbers does not form an AP.

7. 0, -4, -8, -12, ….
a₂ – a₁ = (-4) – 0 = -4,
a₃ – a₂ = (-8) – (-4) = -4,
a₄ – a₃ = (-12) – (-8) = -4
Here, a_k+1 – a_k is the same everywhere.
Hence, the given list of numbers forms an AP with d = -4.
Next three terms are given by-
a₅ = (-12) + (-4) = -16,
a₆ = (-16) + (-4) = -20 and
a₇ = (-20) + (-4) = -24.

8.

Here, a_k+1 – a_k is the same everywhere. Hence, the given list of numbers forms an AP with d = 0.
Next three terms are given by-

9. 1, 3, 9, 27, ….
a₂ – a₁ = 3 – 1 = 2,
a₃ – a₂ = 9 – 3 = 6
Here, a₂ – a₁ ≠ a₃ – a₂
Hence, the given list of numbers does not form an AP.

10. a, 2a, 3a, 4a…
a₂ – a₁ = 2a – a = a,
a₃ – a₂ = 3a – 2a = a.
a₄ – a₃ = 4a – 3a = a
Here, a_k+1 – a_k is the same everywhere.
Hence, the given list of unknown numbers forms an AP with d = a.
Next three terms are given by-
a₅ = 4a + a = 5a,
a₆ = 5a + a = 6a and
a₇ = 6a + a = 7a

11. a, a², a³, a⁴,….
a₂ – a₁ = a² – a = a (a – 1),
a₃ – a₂ = a³ – a² = a² (a – 1)
Here, a₂ – a₁ ≠ a₃ – a₂.
Hence, the given list of unknown numbers does not form an AP.

12. \(\sqrt{2}\), \(\sqrt{8}\), \(\sqrt{18}\), \(\sqrt{32}\), ….
We know, \(\sqrt{8}\) = \(\sqrt{4 \times 2}\) = 2\(\sqrt{2}\).
\(\sqrt{18}\) = \(\sqrt{9 \times 2}\) = 3\(\sqrt{2}\) and
\(\sqrt{32}\) = \(\sqrt{16 \times 2}\) = 4\(\sqrt{2}\).
Hence, the given list of numbers is
\(\sqrt{2}\), 2\(\sqrt{2}\), 3\(\sqrt{2}\), 4\(\sqrt{2}\), ….
a₂ – a₁ = 2\(\sqrt{2}\) – \(\sqrt{2}\) = \(\sqrt{2}\),
a₃ – a₂= 3\(\sqrt{2}\) – 2\(\sqrt{2}\) = \(\sqrt{2}\)
a₄ – a₃ = 4\(\sqrt{2}\) – 3\(\sqrt{2}\) = \(\sqrt{2}\)
Here, a_k+1 – a_k is the same everywhere.
Hence, the given list of numbers forms an AP with d = \(\sqrt{2}\).
Next three terms are given by-
a₅ = 4\(\sqrt{2}\) + \(\sqrt{2}\) = 5\(\sqrt{2}\) = \(\sqrt{50}\).
a₆ = 5\(\sqrt{2}\) + \(\sqrt{2}\) = 6\(\sqrt{2}\) = \(\sqrt{72}\) and
a₇ = 6\(\sqrt{2}\) + \(\sqrt{2}\) = 7\(\sqrt{2}\) = \(\sqrt{98}\).

13. \(\sqrt{3}\), \(\sqrt{6}\), \(\sqrt{9}\), \(\sqrt{12}\), ……
a₂ – a₁ = \(\sqrt{6}\) – \(\sqrt{3}\) = \(\sqrt{3}\)(\(\sqrt{2}\) – 1)
a₃ – a₂ = \(\sqrt{9}\) – \(\sqrt{6}\) = \(\sqrt{3}\)(\(\sqrt{3}-\sqrt{2}\))
Here, a₂ – a₁ ≠ a₃ – a₂
Hence, the given list of numbers does not form an AP.

14. 1², 3², 5², 7², ….
a₂ – a₁ = 3² – 1² = 9 – 1 = 8,
a₃ – a₂ = 5² – 3² = 25 – 9 = 16
Here, a₂ – a₁ ≠ a₃ – a₂
Hence, the given list of numbers does not form an AP.

15. 1², 5², 7², 7²,…
a₂ – a₁ = 5² – 1² = 25 – 1 = 24,
a₃ – a₂ = 7² – 5² = 49 – 25 = 24,
a₄ – a₃ = 73 – 7² = 73 – 49 = 24.
Here. a_k+1 – a_k is the same everywhere.
Hence, the given list of numbers forms an AP with d = 24.
Next three terms are given by-
a₅ = 73 + 24 = 97,
a₆ = 97 + 24 = 121 and
a₇ = 121 + 24 = 145.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 Quadratic Equations Ex 4.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 Quadratic Equations Exercise 4.4

Question 1.
Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:
1. 2x² – 3x + 5 = 0
2. 3x² – 4\(\sqrt{3}\)x + 4 = 0
3. 2x² – 6x + 3 = 0
Solution:
The given equation is of the form
ax² + bx + c = 0; where a = 2, b = -3 and c = 5.
Then, the discriminant
b² – 4ac = (-3)² – 4(2)(5)
= 9 – 40
= -31 <0
So, the given equation has no real roots.

2. Comparing the given equation with the standard quadratic equation
ax² + bx + c = 0, we get a = 3, b = -4\(\sqrt{3}\) and c = 4.
Then, the discriminant
b² – 4ac = (-4\(\sqrt{3}\))² – 4(3)(4)
= 48 – 48
= 0
So, the given equation has equal real roots.
The roots are \(-\frac{b}{2 a},-\frac{b}{2 a}\)
i.e., \(-\frac{-4 \sqrt{3}}{2(3)},-\frac{-4 \sqrt{3}}{2(3)}\), i.e., \(\frac{2}{\sqrt{3}}, \frac{2}{\sqrt{3}}\)

3. The given equation is of the form
ax² + bx + c = 0, where a = 2, b = -6 and c = 3.
Then, the discriminant
b² – 4ac = (-6)² – 4(2)(3)
= 36 – 24
= 12
So, the given equation has two distinct roots.
The roots are given by
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
\(=\frac{6 \pm \sqrt{12}}{2(2)}\)
\(=\frac{6 \pm 2 \sqrt{3}}{4}=\frac{3 \pm \sqrt{3}}{2}\)
Thus, the roots of the given equation are \(\frac{3+\sqrt{3}}{2}\) and \(\frac{3-\sqrt{3}}{2}\)

Question 2.
Find the values of k for each of the following quadratic equations, so that they have two equal roots:
1. 2x² + kx + 3 = 0
2. kx (x – 2) + 6 = 0
Solution:
1. Comparing the given equation with the standard quadratic equation, we have
a = 2, b = k and c = 3.
Then, the discriminant = b² – 4ac
= (k)² – 4 (2) (3)
= k² – 24
If the equation has two equal roots, then the discriminant = 0
∴ k² – 24 = 0
∴ k² = 24
∴ k = ±\(\sqrt{24}\)
∴ k ± 2\(\sqrt{6}\)

2. kx(x – 2) + 6 = 0
∴ kx² – 2kx + 6 = 0
Here, a = k, b = -2k and c = 6.
Then, the discriminant = b² – 4ac
= (-2k)² – 4(k)(6)
= 4k² – 24k
If the equation has two equal roots, then the discriminant = 0
∴ 4k² – 24k = 0
∴ 4k (k – 6) = 0
∴ k = 0 or k = 6
But k = 0 is not possible because if k = 0, the equation reduces to 6 = 0, not a quadratic equation.
∴ k = 6

Question 3.
Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m²? If so, find its length and breadth.
Solution:
Considering that the required mango grove can be designed, let the breadth of the mango grove be x m.
Then, the length of the mango grove is 2x m. Area of rectangular mango grove
= Length × Breadth
= 2x × x
= 2x² m²
The required area is 800 m².
∴ 2x² = 800
∴ 2x² – 800 = 0
∴ x² – 400 = 0
If the above equation has real roots, then it is possible to design the required mango grove.
Here, a = 1, b = 0 and c = -400.
Then, the discriminant = b² – 4ac
= (0)² – 4(1)(-400)
= 1600 > 0
Hence, the equation has real roots. So, it is possible to design the mango grove with required measures.
Now, x² – 400 = 0
∴ (x + 20) (x – 20) = 0
∴ x + 20 = 0 or x – 20 = 0
∴ x = -20 or x = 20
Since x is the breadth of the rectangular mango grove, x = -20 is not possible.
∴ x = 20 and 2x = 40
Thus, the length of the mango grove is 40 m and its breadth is 20 m.

Question 4.
Is the following situation possible? If so, determine their present ages.
The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Solution:
Let the present ages of two friends be x years and (20 – x) years.
Four years ago, their respective ages were (x – 4) years and (20 – x – 4) years, i.e., (16 – x) years.
Then, according to given,
(x – 4) (16 – x) = 48
∴ 16x – x² – 64 + 4x = 48
∴ -x² + 20x – 64 – 48 = 0
∴ -x² + 20x – 112 = 0
∴ x² – 20x + 112 = 0
Here, a = 1, b = -20 and c = 112.
Then, the discriminant
b² – 4ac = (-20)² – 4(1)(112)
= 400 – 448
= -48 < 0
Hence, the equation has no real roots. So, the given situation is not possible.

Question 5.
Is it possible to design a rectangular park of perimeter 80 m and area 400 m² ? If so, find its length and breadth.
Solution:
Let the length of the rectangular park be x m.
Perimeter of rectangular park = 2 (Length + Breadth)
∴ 80 = 2(x + Breadth)
∴ 40 = x + Breadth
∴ Breadth = (40 – x) m
Now, area of rectangular park = Length × Breadth
∴ 400 = x (40 – x)
∴ 400 = 40x – x²
∴ x² – 40x + 400 = 0
Here, a = 1, b = -40 and c = 400.
Then, the discriminant = b² – 4ac
= (-40)² – 4(1)(400)
= 1600 – 1600
= 0
Hence, the equation has equal real roots. So, it is possible to design a rectangular park with given measures.
x² – 40x + 400 = 0
∴ x² – 20x – 20x + 400 = 0
∴ x(x – 20) – 20(x – 20) = 0
∴ (x – 20) (x – 20) = 0
∴ x – 20 = 0 or x – 20 = 0
∴ x = 20 or x = 20
Thus, the length of the rectangular park = x = 20 m and the breadth of the rectangular park = 40 – x = 40 – 20 = 20 m.
Note: Here the shape of the park turns out to be a square, but as we know, every square is a rectangle.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 Triangles Ex 6.5 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 6 Triangles Exercise 6.5

Question 1.
Sides of triangles are given below, Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse:
1. 7 cm, 24 cm, 25 cm
2. 3 cm, 8 cm, 6 cm
3. 50 cm, 80 cm, 100 cm
4. 13 cm, 12 cm, 5 cm
Solution :
1. 7 cm, 24 cm, 25 cm.
Here, the longest side is 25 cm.
25² = 625 and 7² + 24² = 49 + 576 = 625
∴ 25² = 7² + 24²
Here, the square of the longest side equals the sum of squares of the other two sides. Hence, the triangle with sides 7 cm, 24 cm and 25 cm is a right triangle and the length of its hypotenuse, is 25 cm.

2. 3 cm, 8 cm, 6 cm
Here, the longest side is 8 cm.
8² = 64 and 3² + 6² = 9 + 36 = 45
∴ 8² ≠ 3² + 6²
Hence, the triangle with sides 3 cm, 8 cm and 6 cm is not a right triangle.

3. 50 cm, 80 cm, 100 cm
Here, the longest side is 100 cm.
100² = 10000 and
50² + 80² = 2500 + 6400 = 8900
∴ 100² ≠ 50² + 80²
Hence, the triangle with sides 50 cm, 80 cm and 100 cm is not a right triangle.

4. 13 cm, 12 cm, 5 cm
Here, the longest side is 13 cm.
13² = 169 and 12² + 5² = 144 + 25 = 169
∴ 13² = 12² + 5²
Here, the square of the longest side equals the sum of squares of the other two sides. Hence, the triangle with sides 13 cm. 12 cm and 5 cm is a right triangle and the length of its hypotenuse is 13 cm.

Question 2.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM² = QM. MR.
Solution :

PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR.
∴ ΔRMP ~ ΔPMQ ~ ΔRPQ (Theorem 6.7)
Now, ΔRMP ~ ΔPMQ
∴ \(\frac{PM}{QM}=\frac{RM}{PM}\)
∴ PM² = QM. MR

Question 3.
In the given figure, ABD is a triangle right-angled at A and AC ⊥ BD. Show that
1. AB² = BC.BD
2. AC² = BC.DC
3. AD² = BD.CD
Solution :

ABD is a triangle right angled at A and AC ⊥ BD.
∴ ΔBCA ~ ΔACD ~ ΔBAD (Theorem 6.7)
1. ΔBCA ~ ΔBAD
∴ \(\frac{AB}{DB}=\frac{CB}{AB}\)
∴ AB² = BC. BD

2. ΔBCA ~ ΔACD
∴ \(\frac{AC}{DC}=\frac{BC}{AC}\)
∴ AC² = BC. DC

3. ΔACD ~ ΔBAD
∴ \(\frac{AD}{BD}=\frac{CD}{AD}\)
∴ AD² = BD . CD

Question 4.
ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².
Solution :
ABC is an isosceles triangle right angled at C.
Hence, AB is the hypotenuse and the other two sides are equal, i.e., BC = AC
In ΔABC, ∠C = 90°

∴ By Pythagoras theorem,
AB² = BC² + AC²
∴ AB² = AC² + AC² (∵ BC = AC)
∴ AB² = 2AC²

Question 5.
ABC is an isosceles triangle with AC = BC. If AB² = 2AC², prove that ABC is a right triangle.
Solution :
In ΔABC, AC = BC and AB² = 2AC²
AB² = 2AC²
∴ AB² = AC² + AC²
∴ AB² = AC² + BC² (∵ AC = BC)
Hence, by the converse of Pythagoras theorem, ΔABC is right triangle in which ∠C is a right angle.

Question 6.
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution :

In ΔABC, AB = BC = CA = 2a.
Let AD be its altitude
∴ ∠ADB = ∠ADC = 90°
In ΔADB and ΔADC,
∠ADB = ∠ADC = 90°
AB = AC
AD = AD
∴ By RHS criterion,
= ΔADC
∴ BD = CD
But, BD + CD = BC
∴ BD = CD = \(\frac{1}{2}\)BC = \(\frac{1}{2}\)(2a) = a
Now, in ΔADB, ∠D = 90°
∴ By Pythagoras theorem,
AB² = AD² + BD²
∴ (2a)² = AD² + (a)²
∴ 4a² – a² = AD²
∴ AD² = 3a²
∴ AD = \(\sqrt{3}\)a
All the altitudes of an equilateral triangle are equal.
Hence, each of the altitudes of equilateral ΔABC with side 2a is \(\sqrt{3}\)a.

Question 7.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Solution :
Given: ABCD is a rhombus.
To prove : AB² + BC² + CD² + DA² = AC² + BD²

Proof: ABCD is a rhombus.
∴ AB = BC = CD = DA ……………(1)
Let its diagonals AC and BD intersect at M.
Then, MA = MC = \(\frac{1}{2}\)AC.
MB = MD = \(\frac{1}{2}\)BD and
∠AMB = ∠BMC = ∠CMD = ∠DMA = 90°
In ΔAMB, ∠AMB = 90°
∴ AB² = MA² + MB² (Pythagoras theorem)
∴ AB² = (\(\frac{AC}{2}\))² + (\(\frac{BD}{2}\))²
∴ AB² = (\(\frac{AC}{2}\))² + (\(\frac{BD}{2}\))²
∴ 4AB² = \(\frac{\mathrm{AC}^2}{4}+\frac{\mathrm{BD}^2}{4}\)
∴ 4AB² = AC² + BD²
∴ AB² + AB² + AB² + AB² = AC² + BD²
∴ AB² + BC² + CD² + DA² = AC² + BD²

Question 8.
In the given figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:
1. OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
2. AF² + BD² + CE² = AE² + CD² + BF².
Solution :

Join OA, OB and OC.
Here, in ΔOFA and ΔOFB, ∠F = 90°, in ΔODB and ΔODC, ∠D = 90° and in ΔOEC and ΔOEA. ∠E = 90°.
Then, Pythagoras theorem is applicable in all the triangles.
1. In ΔOFA, ∠F = 90°
∴ OA² = OF² + AF²
∴ AF² = OA² – OF² …………..(1)
In ΔODB, ∠D = 90°
∴ OB² = OD² + BD²
∴ BD² = OB² – OD² …………..(2)
In ΔOEC, OE² + CE²
∴ CE² = OC² – OE² …………..(3)
Adding (1), (2) and (3).
AF² + BD² + CE² = OA² – OF² + OB² – OD² + OC² – OE²
∴ OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²

2. AF² + BD² + CE² = OA² + OB² + OC² – OD² – OE² – OF²
∴ AF² + BD² + CE² = (OA² – OE²) + (OB² – OF²) + (OC² – OD²)
∴ AF² + BD² + CE² = AE² + BF² + CD² (∵ ΔOAE, ΔOBF and ΔOCD are right triangles)
∴ AF² + BD² + CE² = AE² + CD² + BF²

Question 9.
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Solution :

Here, AB is the wall with window at point A and AC is the ladder.
Then, AC = 10m and AB = 8 m.
In ΔABC, ∠B = 90°.
∴ AC² = AB² + BC² (Pythagoras theorem)
∴ 10² = 8² + BC²
∴ BC² = 10² – 8²
∴ BC² = 100 – 64
∴ BC² = 36
∴ BC = 6 m
Thus, the distance of the foot of the ladder from the base of the wall is 6 m.

Question 10.
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Solution :

Here, AB is the vertical pole in which the guy wire is attached at point A and AC is the guy wire and 18 m the stake is attached to its end C.
Then, AC = 24 m and AB = 18 m.
In ΔABC, ∠B = 90°
∴ AC² = AB² + BC² (Pythagoras theorem)
∴ 24² = 18² + BC²
∴ BC² = 576 – 324
∴ BC² = 252
∴ BC² = 4 × 9 × 7
∴ BC = 2 × 3 × \(\sqrt{7}\)
∴ BC = 6\(\sqrt{7}\) m
Thus, the stake should be driven 6\(\sqrt{7}\)m far from the base of the pole, so as to make the wire taut.

Question 11.
An airplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another airplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1\(\frac{1}{2}\) hours?
Solution :

Here, A is the airport, B is the position of the first plane flying due north after 1\(\frac{1}{2}\) hours and C is the position of the second c- plane flying due west after 1\(\frac{1}{2}\) hours.
[Note: For the sake of simplicity, we consider that both the planes are flying at the same height and point A representing the airport is also imagined to be at the same height.]
Then, AB = distance covered by the first plane in 1\(\frac{1}{2}\) hours
= Speed × Time
= 1000 × \(\frac{3}{2}\)
= 1500 km
Similarly, AC = distance covered by the second plane in 1\(\frac{1}{2}\) hours
= Speed × Time
= 1200 × \(\frac{3}{2}\)
= 1800 km
Also, ∠BAC is the angle formed by north direction and west direction.
Hence ∠BAC = 90°
Now, in ΔABC, ∠A = 90°
∴ BC² = AB² + AC² (Pythagoras theorem)
∴ BC² = (1500)² + (1800)²
∴ BC² = 22500 + 32400
∴ BC² = 54900
∴ BC = \(\sqrt{100 \times 9 \times 61}\)
∴ BC = 300\(\sqrt{61}\) km
Thus, the two planes will be 300\(\sqrt{61}\) km apart from each other after 1\(\frac{1}{2}\) hours.

Question 12.
Two poles of heights 6m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Solution :

Here, AB and CD are two erect poles of height 6 m and 11 m respectively.
The distance between the feet of the poles is 12 m.
Then, AB = 6 m, BD = 12 m, CD = 11 m, ∠B = 90° and ∠D = 90°.
Draw AE || BC.
Then, in quadrilateral ABDE.
∠B = ∠D = ∠E = ∠A = 90°.
Hence, ABDE is a rectangle.
∴ ED = AB = 6m and AE = BD = 12 m.
Then, CE = CD – DE = 11 – 6 = 5m
Now, in ΔAEC, ∠E = 90°.
∴ AC² = AE² + CE² (Pythagoras theorem)
∴ AC² = 12² + 5²
∴ AC² = 144 + 25
∴ AC² = 169
∴ AC = 13 m
Thus, the distance between the tops of the vertical poles is 13 m.

Question 13.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE²
Solution :
In ΔABC, ∠C is a right angle, point D lies on CA and point E lies on CB.

Then, all the four triangles BCD, BCA, ECD and ECA are right triangles and in each of them C is a right angle.
Hence, Pythagoras theorem is applicable in all the four triangles.
In ΔECA, AE² = EC² + CA² ……………..(1)
In ΔBCD, BD² = BC² + CD² ……………..(2)
In ΔBCA, AB² = BC² + CA² ……………..(3)
In ΔECD, DE² = EC² + CD² ……………..(4)
Adding (1) and (2).
AE² + BD² = EC² + CA² + BC² + CD²
= (BC² + CA²) + (EC² + CD²)
= AB² + DE² [By (3) and (4)]
Thus, AE² + BD² = AB² + DE²

Question 14.
The perpendicular from A on side BC of a ΔABC intersects BC at D such that DB = 3CD (see the given figure). Prove that 2AB² = 2AC² + BC².
Solution :

DB = 3CD
∴ BC = DB + CD = 3CD + CD
∴ BC = 4CD …………..(1)
In ΔADB, ∠D = 90°
∴ AB² = AD² + DB² (Pythagoras theorem) …………..(2)
In ΔADC, ∠D = 90°
∴ AC² = AD² + CD² (Pythagoras theorem) …………..(3)
Subtracting (3) from (2),
AB² – AC² = (AD² + DB²) – (AD² + CD²)
∴ AB² – AC² = DB² – CD²
∴ AB² – AC² = (DB + CD) (DB – CD)
∴ AB² – AC² = (BC) (3CD – CD)
∴ AB² – AC² = (BC) (2CD)
Multiplying the equation by 2, we get
2AB² – 2AC² = (BC) (4CD)
∴ 2AB² – 2AC² = (BC) (BC)
∴ 2AB² = 2AC² + BC² [By (1)]

Question 15.
In an equilateral triangle ABC, D is a point on side BC such that BD = \(\frac{1}{3}\)BC. Prove that 9AD² = 7AB².
Solution :
Given: In equilateral ΔABC, D is a point on BC such that BD = \(\frac{1}{3}\)BC.
To prove: 9AD² = 7AB²

Construction: Draw AM ⊥ BC, such that M lies on BC.
Proof: ΔABC is an equilateral triangle. Suppose, AB = BC = AC = a
In equilateral ΔABC, AM is an altitude.
∴ AM is a median.
∴ BM = \(\frac{1}{2}\)BC = \(\frac{1}{2}\)a
∴ BD = \(\frac{1}{3}\)BC. Hence, DC = \(\frac{2}{3}\)BC
BD = \(\frac{1}{3}\)BC = \(\frac{1}{3}\)a
DM = BM – BD = \(\frac{1}{2}\)a – \(\frac{1}{3}\)a = \(\frac{1}{6}\)a
In ΔAMB, ∠M = 90°
∴ AB² = AM² + BM²
∴ a² = AM² + \(\frac{1}{4}\)a²
∴ AM² = \(\frac{3}{4}\)a²
In ΔAMD, ∠M = 90°
∴ AD² = AM² + DM²

∴ 9AD² = 7a²
∴ 9AD2 = 7AB² (∵ AB = a)

Question 16.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution :

ABC is an equilateral triangle in which AD is an altitude.
Let AB = BC CA- a units.
In an equilateral triangle, an altitude is a median also.
∴ AD is a median.
∴ BD = \(\frac{1}{2}\)BC = \(\frac{a}{2}\)units
In ΔADB, ∠D = 90°
∴ AB² = AD² + BD²
∴ (a)² = AD² + (\(\frac{a}{2}\))²
∴ a² = AD² + \(\frac{a^2}{4}\)
∴ \(\frac{3}{4}\)a² = AD²
∴ 3a² = 4AD²
∴ 3 (side)² = 4 (altitude)²

Question 17.
Tick the correct answer and justify: In ΔABC, AB = 6\(\sqrt{3}\) cm, AC = 12 cm and BC= 6 cm. The angle B is:
(A) 120°
(B) 60°
(C) 90°
(D) 45°
Solution :
In ΔABC, AB = 6\(\sqrt{3}\) cm = 10.38 cm (approx),
AC = 12 cm and BC = 6 cm
Here, AC is the longest side.
Then, 12² = 144 and
(6\(\sqrt{3}\))² + (6)² – 108 + 36 = 144
Thus, 12² = (6\(\sqrt{3}\))² + (6)²
Hence, by the converse of Pythagoras theorem, ΔABC is a right triangle in which the longest side AC is the hypotenuse and its opposite angle ∠B is a right angle.
Hence, the correct answer is (C) 90°.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 Quadratic Equations Ex 4.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 Quadratic Equations Exercise 4.3

Question 1.
Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
1. 2x² – 7x + 3 = 0
2. 2x² + x – 4 = 0
3. 4x² + 4\(\sqrt{3}\)x + 3 = 0
4. 2x² + x + 4 = 0
Solution:
1. 2x² – 7x + 3 = 0
Dividing throughout by 2, we get

Thus, the roots of the given quadratic equation are 3 and \(\frac{1}{2}\).

2. 2x² + x – 4 = 0
Dividing throughout by 2, we get

Thus, the roots of the given quadratic equation are \(\frac{-1+\sqrt{33}}{4}\) and \(\frac{-1-\sqrt{33}}{4}\)

3. 4x² + 4\(\sqrt{2}\)x + 3 = 0
4x² + 4\(\sqrt{3}\)x + (\(\sqrt{3}\))² = 0
(2x + \(\sqrt{3}\))² = 0
(2x + \(\sqrt{3}\)) (2x + \(\sqrt{3}\)) = 0
2x + \(\sqrt{3}\) = 0 or 2x + \(\sqrt{3}\) =0
x = \(-\frac{\sqrt{3}}{2}\) or x = \(-\frac{\sqrt{3}}{2}\)
Thus, the roots of the given quadratic equation are \(-\frac{\sqrt{3}}{2}\) and \(-\frac{\sqrt{3}}{2}\)

4. 2x² + x + 4 = 0
Dividing throughout by 2, we get

But, the square of any real number cannot be negative.
Hence, the real roots of the given quadratic equation do not exist.

Question 2.
Find the roots of the quadratic equations given in Q.1 by applying the quadratic formula.
1. 2x² – 7x + 3 = 0
Here, a = 2, b = -7 and c = 3.
Then, b² – 4ac = (-7)² – 4(2)(3) = 25
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ x = \(\frac{7 \pm \sqrt{25}}{2(2)}\)
∴ x = \(\frac{7 \pm 5}{4}\)
∴ x = 3 or x = \(\frac{1}{2}\)
Thus, the roots of the given quadratic equation are 3 and \(\frac{1}{2}\).

2. 2x² + x – 4 = 0
Here, a = 2, b = 1 and c = -4.
Then, b² – 4ac = (1)² – 4(2)(-4) = 33
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ x = \(\frac{-1 \pm \sqrt{33}}{2(2)}\)
∴ x = \(\frac{-1 \pm \sqrt{33}}{4}\)
Thus, the roots of the given quadratic equation are \(\frac{-1 \pm \sqrt{33}}{4}\) and \(\frac{-1-\sqrt{33}}{4}\)

3. 4x² + 4\(\sqrt{3}\)x + 3 = 0
Here, a = 4, b = 4\(\sqrt{3}\) and c = 3.
Then, b² – 4ac = (4\(\sqrt{3}\))² – 4(4)(3) = 0
Then, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ x = \(\frac{-4 \sqrt{3} \pm \sqrt{0}}{2(4)}\)
∴ x = \(-\frac{\sqrt{3}}{2}\) or x = \(-\frac{\sqrt{3}}{2}\)
Thus, the roots of the given quadratic equation are \(-\frac{\sqrt{3}}{2}\) and \(-\frac{\sqrt{3}}{2}\).

4. 2x² + x + 4 = 0
Here, a = 2, b = 1 and c = 4.
Then, b² – 4ac = (1)² – 4 (2)(4) = -31 < 0
Since b² – 4ac < 0 for the given quadratic equation, the real roots of the given quadratic equation do not exits.

Question 3.
Find the roots of the following equations:
1. x – \(\frac{1}{x}\) = 3, x ≠ 0
2. \(\frac{1}{x+4}-\frac{1}{x-7}=\frac{11}{30}\); x ≠ -4, 7
Solution:
1. x – \(\frac{1}{x}\) = 3, x ≠ 0
∴ x² – 1 = 3x
∴ x² – 3x – 1 = 0
Here, a = 1, b = -3 and c = -1.
Then, b² – 4ac = (-3)² – 4(1)(-1) = 13
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
x = \(\frac{3 \pm \sqrt{13}}{2(1)}\)
x = \(\frac{3 \pm \sqrt{13}}{2}\)
Thus, the roots of the given equation are \(\frac{3+\sqrt{13}}{2}\) and \(\frac{3-\sqrt{13}}{2}\).

2. \(\frac{1}{x+4}-\frac{1}{x-7}=\frac{11}{30}\); x ≠ -4, 7
∴ \(\frac{(x-7)-(x+4)}{(x+4)(x-7)}=\frac{11}{30}\)
∴ \(\frac{-11}{x^2-3 x-28}=\frac{11}{30}\)
∴ \(\frac{-1}{x^2-3 x-28}=\frac{1}{30}\)
∴ -30 = x² – 3x – 28
∴ x² – 3x + 2 = 0
Here, a = 1, b = -3 and c = 2.
Then, b² – 4ac = (-3)² – 4(1)(2) = 1
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ x = \(\frac{3 \pm \sqrt{1}}{2(1)}\)
∴ x = \(\frac{3 \pm 1}{2}\)
∴ x = 2 or x = 1
Thus, the roots of the given equation are 2 and 1.
Note: Here, the method of factorisation would turn out to be more easier.

Question 4.
The sum of the reciprocals of Rehman’s ages (in years), 3 years ago and 5 years from now is \(\frac{1}{3}\). Find his present age.
Solution:
Let the present age of Rehman be x years.
So, his age 3 years ago was (x – 3) years and his age 5 years hence will be (x + 5) years.
The sum of the reciprocals of these two ages (in years) is given to be \(\frac{1}{3}\).
∴ \(\frac{1}{x-3}+\frac{1}{x+5}=\frac{1}{3}\)
∴ \(\frac{x+5+x-3}{(x-3)(x+5)}=\frac{1}{3}\)
∴ 3(2x + 2) = (x – 3)(x + 5)
∴ 6x + 6 = x² + 2x – 15
∴ x² – 4x – 21 = 0
∴ x² – 7x + 3x – 21 = 0
∴ x(x – 7) + 3(x – 7) = 0
∴ (x – 7)(x + 3) = 0
∴ x – 7 = 0 or x + 3 = 0
∴ x = 7 or x = -3
Now, since x represents the present age of Rehman, it cannot be negative, i,e., x ≠ -3.
∴ x = 7
Thus, the present age of Rehman is 7 years.

Question 5.
In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of those marks would have been 210. Find her marks in the two subjects.
Solution:
Let Shefali’s marks in Mathematics be x.
Then, her marks in English = 30 – x, as her total marks in Mathematics and English is 30.
Had she scored 2 marks more in Mathematics and 3 marks less in English, her score in Mathematics would be x + 2 and in English would be 30 – x – 3 = 27 – x.
∴ (x + 2) (27 – x) = 210
∴ 27x – x² + 54 – 2x = 210
∴ -x² + 25x + 54 – 210 = 0
∴ -x² + 25x – 156 = 0
∴ x² – 25x + 156 = 0
∴ x² – 13x – 12x + 156 = 0
∴ x(x – 13) – 12(x – 13) = 0
∴ (x – 13)(x – 12) = 0
∴ x – 13 = 0 or x – 12 = 0
∴ x = 13 or x = 12
Then, 30 – x = 30 – 13 = 17 or
30 – x = 30 – 12 = 18
Thus, Shefall’s marks in Mathematics and in English are 13 and 17 respectively or 12 and 18 respectively.

Question 6.
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Solution:
Let the shorter side of the rectangular field be x m.
Then, it diagonal is (x + 60) m and the longer side is (x + 30) m.
In a rectangle, all the angles are right angles.
Hence, by Pythagoras theorem,
(Shorter side)² + (Longer side)² = (Diagonal)²
∴ x² + (x + 30)² = (x + 60)²
∴ x² + x² + 60x + 900 = x² + 120x + 3600
∴ x² – 60x – 2700 = 0
Here, a = 1, b = -60 and c = -2700.
Then, b² – 4ac = (-60)² – 4(1)(-2700)
= 3600 + 10800
= 14400
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{60 \pm \sqrt{14400}}{2(1)}\)
= \(\frac{60 \pm 120}{2}\)
∴ x = \(\frac{60+120}{2}\) or x = \(\frac{60-120}{2}\)
∴ x = 90 or x = -30
Since x denotes the shorter side of the rectangular field, x cannot be negative.
∴ x = 90
Then, x + 30 = 90 + 30 = 120
Thus, the shorter side (breadth) of the rectangular field is 90 m and the longer side (length) of the rectangular field is 120 m.

Question 7.
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
Solution:
Let the smaller number be x.
Then, the larger number = \(\frac{x^2}{8}\)
Now, the difference of their squares is 180.
∴ \(\left(\frac{x^2}{8}\right)^2-(x)^2=180\)
∴ \(\frac{x^4}{64}-x^2=180\)
∴ x⁴ – 64x² – 11520 = 0
Let x² = y
∴ x⁴ = y²
∴ y² – 64y – 11520 = 0
Here, a = 1, b = -64 and c = -11520.
Then, b² – 4ac = (-64)² – 4(1)(-11520)
= 4096 + 46080
= 50176
Now, y = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{64 \pm \sqrt{50176}}{2(1)}\)
= \(\frac{64 \pm 224}{2}\)
∴ y = \(\frac{64+224}{2}\) or y = \(\frac{64-224}{2}\)
∴ y = 144 or y = -80
∴ x² = 144 or x² = -80
But, x² = -80 is not possible.
∴ x² = 144
∴ x = 12 or x = -12
Then, \(\frac{x^2}{8}=\frac{144}{8}=18\)
Thus, the required numbers are 12 and 18 or -12 and 18.

Question 8.
A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution:
Let the usual uniform speed of the train be x km/h.
∴ Time taken to travel 360 km at the speed of x km/h = \(\frac{\text { distance }}{\text { speed }}\) = \(\frac{360}{x}\) hours.
If the speed had been 5 km/h more, the new speed would be (x + 5) km/h and the time taken to travel 360 km at this increased speed would be \(\frac{360}{x+5}\) hours.
Now, New time = Usual time – 1
∴ \(\frac{360}{x+5}=\frac{360}{x}-1\)
∴ 360x = 360x + 1800 – x(x + 5) (Multiplying by x(x + 5))
∴ 0 = 1800 – x² – 5x
∴ x² + 5x – 1800 = 0
∴ x² + 45x – 40x – 1800 = 0
∴ x(x + 45) – 40(x + 45) = 0
∴ (x + 45) (x – 40) = 0
∴ x + 45 = 0 or x – 40 = 0
∴ x = -45 or x = 40
As, x is the speed (in km/h) of the train, x = -45 is not possible.
∴ x = 40
Thus, the usual uniform speed of the train is 40 km/h.

Question 9.
Two water taps together can fill a tank in \(9 \frac{3}{8}\) hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution:
Let the time taken by the tap with smaller diameter to fill the tank be x hours.
Then, the time taken by the tap with larger diameter = (x – 10) hours.
So, the part of the tank filled in one hour by the tap with smaller diameter = \(\frac{1}{x}\) and by the tap with larger diameter = \(\left(\frac{1}{x-10}\right)\)
So, the part of tank filled in one hour by both the taps together = \(\frac{1}{x}+\frac{1}{x-10}\)
Both the taps together can fill the tank in \(9 \frac{3}{8}\) hours, i.e., \(\frac{75}{8}\) hours.
∴ The part of tank filled in one hour by both the tank together = \(\frac{8}{75}\)
∴ \(\frac{1}{x}+\frac{1}{x-10}=\frac{8}{75}\).
∴ 75(x – 10) + 75x = 8x (x – 10) (Multiplying by 75x(x – 10))
∴ 75x – 750 + 75x = 8x² – 80x
∴ 8x² – 230x + 750 = 0
Here, a = 8, b = -230 and c = 750.
∴ b² – 4ac = (-230)² – 4 (8)(750)
= 52900 – 24000
= 28900
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ x = \(\frac{230 \pm \sqrt{28900}}{2(8)}\)
∴ x = \(\frac{230 \pm 170}{16}\)
∴ x = \(\frac{400}{16}\) or x = \(\frac{60}{16}\)
∴ x = 25 or x = 3.75
But, x ≠ 3.75, because for x = 3.75, x – 10 < 0.
∴ x = 25 and x – 10 = 15
Thus, the time taken by the tap with smaller diameter is 25 hours and that by the tap. with larger diameter is 15 hours.

Question 10.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.
Solution:
Let the average speed of the passenger train be x km/h.
Then, the average speed of the express train is (x + 11) km/h.
∴ Time taken by passenger train to cover 132 km = \(\frac{132}{x}\) hours.
∴ Time taken by express train to cover 132 km = \(\frac{132}{x+11}\) hours.
Time taken by express train = Time taken by passenger train – 1
\(\frac{132}{x+11}=\frac{132}{x}-1\)
∴ 132x = 132(x + 11) – x(x + 11) (Multiplying by x(x + 11))
∴ 132x = 132x + 1452 – x² – 11x
∴ x² + 11x – 1452 = 0
Here, a = 1, b = 11 and c = -1452.
∴ b² – 4ac = (11)² – 4(1)(-1452)
= 121 + 5808 = 5929
Now, x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
∴ x = \(\frac{-11 \pm \sqrt{5929}}{2(1)}\)
∴ x = \(\frac{-11 \pm 77}{2}\)
x = 33 or x = -44
x = -44 is inadmissible as x represents the speed of the passenger train.
∴ x = 33 and x + 11 = 44
Thus, the speed of the passenger train is 33 km/h and the speed of the express train is 44 km/h.

Question 11.
Sum of the areas of two squares is 468 m². If the difference of their perimeters is 24 m, find the sides of the two squares.
Solution:
Let the side of the smaller square be x m.
Then, the perimeter of the smaller square = 4x m
and the area of the smaller square = x² m².
From the given, the perimeter of the bigger square = (4x + 24) m.
∴ Side of the bigger square = \(\frac{4 x+24}{4}\) = (x + 6) m and hence, the area of the bigger square = (x + 6)² m².
∴ x² + (x + 6)² = 468
∴ x² + x² + 12x + 36 – 468 = 0
∴ 2x² + 12x – 432 = 0
∴ x² + 6x – 216 = 0
∴ x² + 18x – 12x – 216 = 0
∴ x(x + 18) – 12(x + 18) = 0
∴ (x + 18) (x – 12) = 0
∴ x + 18 = 0 or x – 12 = 0
∴ x = -18 or x = 12
Here, x = -18 is not possible as x represents the side of a square.
∴ x = 12 and x + 6 = 18
Thus, the side of the smaller square is 12 m and the side of the bigger square is 18 m.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 Quadratic Equations Ex 4.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 Quadratic Equations Exercise 4.2

Question 1.
Find the roots of the following quadratic equations by factorisation:
1. x² – 3x – 10 = 0
2. 2x² + x – 6 = 0
3. \(\sqrt{2}\)x² + 7x + 5\(\sqrt{2}\) = 0
4. 2x² – x + \(\frac{1}{8}\) = 0
5. 100x² – 20x + 1 = 0
Solution:
1. x² – 3x – 10 = 0
∴ x² – 5x + 2x – 10 = 0
∴ x(x – 5) + 2(x – 5) = 0
∴ (x – 5)(x + 2) = 0
Hence, x – 5 = 0 or x + 2 = 0
∴ x = 5 or x = -2
Thus, the roots of the given equation are 5 and -2.
Verification:
For x = 5,
LHS = (5)² – 3(5) – 10
= 25 – 15 – 10
= 0
= RHS
For x = -2,
LHS = (2)² – 3(-2) – 10
= 4 + 6 – 10
= 0
= RHS
Hence, both the roots are verified.
Note that verification is not a part of the solution. It is meant only for your confirmation of receiving correct solution.

2. 2x² + x – 6 = 0
∴ 2x² + 4x – 3x – 6 = 0
∴ 2x (x + 2) – 3(x + 2) = 0
∴ (x + 2) (2x – 3) = 0
∴ x + 2 = 0 or 2x – 3 = 0
∴ x = -2 or x = \(\frac{3}{2}\)
Thus, the roots of the given equation are -2 and \(\frac{3}{2}\)

3. \(\sqrt{2}\)x² + 7x + 5\(\sqrt{2}\) = 0
∴ \(\sqrt{2}\)x² + 2x + 5x + 5\(\sqrt{2}\) = 0
∴ \(\sqrt{2}\)x(x + \(\sqrt{2}\)) + 5(x + \(\sqrt{2}\)) = 0
∴ (x + \(\sqrt{2}\))(\(\sqrt{2}\)x + 5) = 0
∴ x + \(\sqrt{2}\) = 0 or \(\sqrt{2}\)x + 5 = 0
∴ x = –\(\sqrt{2}\) or x = \(-\frac{5}{\sqrt{2}}\)
Thus, the roots of the given equation are –\(\sqrt{2}\) and \(-\frac{5}{\sqrt{2}}\)

4. 2x² – x + \(\frac{1}{8}\) = 0
∴ 16x² – 8x + 1 = 0 (Multiplying by 8)
∴ 16x² – 4x – 4x + 1 = 0
∴ 4x(4x – 1) -1 (4x – 1) = 0
∴ (4x – 1) (4x – 1) = 0
∴ 4x – 1 = 0 or 4x – 1 = 0
∴ x = \(\frac{1}{4}\) or x = \(\frac{1}{4}\)
Thus, the repeated roots of the given equation are \(\frac{1}{4}\) and \(\frac{1}{4}\)

5. 100x² – 20x + 1 = 0
100x² – 10x – 10x + 1 = 0
10x(10x – 1) -1 (10x – 1) = 0
(10x – 1)(10x – 1) = 0
10x – 1 = 0 or 10x – 1 = 0
x = \(\frac{1}{10}\) or x = \(\frac{1}{10}\)
Thus, the repeated roots of the given equation are \(\frac{1}{10}\) and \(\frac{1}{10}\).

Question 2.
Solve the problems given in Textual Examples:
1. John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. Find out how many marbles they had to start with.
2. A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was ₹ 750. Find out the number of toys. produced on that day.
Solution:
1. Let the number of marbles that John had be x.
Then, the number of marbles that Jivanti had is (45 – x).
After losing 5 marbles, the number of marbles left with John = x – 5.
After losing 5 marbles, the number of marbles left with Jivanti = (45 – x) – 5 = 40 – x.
Therefore, the product of marbles with them is (x – 5) (40 – x), which is given to be 124.
Hence, we get the following equation:
(x – 5)(40 – x) = 124.
∴ 40x – x² – 200 + 5x = 124
∴ -x² + 45x – 324 = 0
∴ x² – 45x + 324 = 0
∴ x² – 36x – 9x + 324 = 0
∴ x(x – 36) – 9(x – 36) = 0
∴ (x – 36)(x – 9) = 0
∴ x – 36 = 0 or x – 9 = 0
∴ x = 36 or x = 9
Here, both the answers are admissible.
∴ 45 – x = 45 – 36 = 9 or
45 – x = 45 – 9 = 36
Thus, the number of marbles with John and Jivanti to start with are 36 and 9 respectively or 9 and 36 respectively.

2. Let the number of toys produced on that day be x.
Therefore, the cost of production (in rupees) of each toy on that day = 55 – x.
So, the total cost of production (in rupees) on that day = x (55 – x).
Hence, x(55 – x) = 750
∴ 55x – x² – 750 = 0
∴ x² – 55x + 750 = 0
∴ x² – 30x – 25x + 750 = 0
∴ x(x – 30) – 25(x – 30) = 0
∴ (x – 30)(x – 25) = 0
∴ x – 30 = 0 or x – 25 = 0
∴ x = 30 or x = 25
Here, both the answers are admissible.
Hence, the number of toys produced on that day is 30 or 25.

Question 3.
Find two numbers whose sum is 27 and product is 182.
Solution:
Let the first of the two numbers whose sum is 27 be x.
Then, the second number is 27 – x and the product of those two numbers is x (27 – x).
Their product is given to be 182.
∴ x (27 – x) = 182
∴ 27x – x² – 182 = 0
∴ x² – 27x + 182 = 0
∴ x² – 14x – 13x + 182 = 0
∴ x(x – 14) – 13(x – 14) = 0
∴ (x – 14)(x – 13) = 0
∴ x – 14 = 0 or x – 13 = 0
∴ x = 14 or x = 13
Here, both the answers are admissible.
Hence, if x = 14, it gives that the first number = x = 14 and the second number = 27 – x = 27 – 14 = 13.
And if x = 13, it gives that the first number = x = 13 and the second number = 27 – x = 27 – 13 = 14.
Thus, in either case, the required numbers are 13 and 14.

Question 4.
Find two consecutive positive integers, sum of whose squares is 365.
Solution:
Let two consecutive positive integers be x and x + 1.
Then, the sum of their squares = (x)² + (x + 1)²
= x² + x² + 2x + 1
= 2x² + 2x + 1
This sum is given to be 365.
∴ 2x² + 2x + 1 = 365
∴ 2x² + 2x – 364 = 0
∴ x² + x – 182 = 0
∴ x² + 14x – 13x – 182 = 0
∴ x(x + 14) – 13(x + 14) = 0
∴ (x + 14)( x- 13) = 0
∴ x + 14 = 0 or x – 13 = 0
∴ x = -14 or x = 13
Since x is a positive integer, x = -14 is inadmissible.
∴ x = 13 and x + 1 = 13 + 1 = 14
Thus, the required consecutive positive integers are 13 and 14.

Question 5.
The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Solution:
Let the base of the right triangle be x cm.
Then, its altitude is (x – 7) cm.
The hypotenuse of the right triangle is given to be 13 cm.
Now, by Pythagoras theorem.
(Base)² + (Altitude)² = (Hypotenuse)²
∴ (x)² + (x – 7)² = (13)²
∴ x² + x² – 14x + 49 = 169
∴ 2x² – 14x – 120 = 0
∴ x² – 7x – 60 = 0
∴ x² – 12x + 5x – 60 = 0
∴ x(x – 12) + 5(x – 12) = 0
∴ (x – 12)(x + 5) = 0
∴ x – 12 = 0 or x + 5 = 0
∴ x = 12 or x = -5
As the base of a triangle cannot be negative. x = -5 is inadmissible.
Hence, x = 12.
Then, the base of the triangle = x = 12 cm and the altitude of the triangle = x – 7 = 12 – 7
= 5 cm.
Thus, the base and the altitude of the given triangle are 12 cm and 5 cm respectively.

Question 6.
A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was 90. find the number of articles produced and the cost of each article.
Solution:
Let the number of pottery articles produced on that day be x.
Then, according to the given, the cost of production (in rupees) of each article = 2x + 3.
Hence, total cost of production (in rupees) on that day = x(2x + 3) = 2x² + 3x.
This total cost of production is given to be ₹ 90.
∴ 2x² + 3x = 90
∴ 2x² + 3x – 90 = 0
∴ 2x² – 12x + 15x – 90 = 0
∴ 2x(x – 6) + 15(x – 6) = 0
∴ (x – 6) (2x + 15) = 0
∴ x – 6 = 0 or 2x + 15 = 0
∴ x = 6 or x = –\(\frac{15}{2}\)
Here, x = –\(\frac{15}{2}\) is inadmissible as x represents the number of articles produced.
Hence, x = 6 and 2x + 3 = 2(6) + 3 = 15.
Thus, the number of pottery articles produced on that day is 6 and the cost of production of each article is ₹ 15.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 4 Quadratic Equations Ex 4.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 4 Quadratic Equations Exercise 4.1

Question 1.
Check whether the following are quadratic equations:
1. (x + 1)² = 2(x – 3)
2. x² – 2x = (-2)(3 – x)
3. (x – 2)(x + 1) = (x – 1)(x + 3)
4. (x – 3)(2x + 1) = x(x + 5)
5. (2x – 1)(x – 3) = (x + 5)(x – 1)
6. x² + 3x + 1 = (x – 2)²
7. (x + 2) = 2x(x² – 1)
8. x³ – 4x² – x + 1 = (x – 2)³
Solution:
1. Here, LHS = (x + 1)² = x² + 2x + 1 and
RHS = 2(x – 3) = 2x – 6.
Hence, (x + 1)² = 2(x – 3) can be rewritten as x² + 2x + 1 = 2x – 6
∴ x² + 2x + 1 – 2x + 6 = 0
∴ x² + 7 = 0
It is of the form ax² + bx + c = 0.
(a = 1, b = 0, c = 7)
Hence, the given equation is a quadratic equation.

2. Here, RHS = (-2)(3 – x) = -6 + 2x.
Hence, x² – 2x = (-2) (3 – x) can be rewritten as
x² – 2x = -6 + 2x
∴ x² – 4x + 6 = 0
It is of the form ax² + bx + c = 0.
(a = 1, b = -4, c = 6)
Hence, the given equation is a quadratic equation.

3. Here, LHS = (x – 2) (x + 1) = x² – x – 2 and
RHS = (x – 1)(x + 3) = x² + 2x – 3.
Hence, (x – 2)(x + 1)(x – 1)(x + 3) be rewritten as
x² – x – 2 = x² + 2x – 3
∴ -3x + 1 = 0
It is not of the form ax² + bx + c = 0.
Hence, the given equation is not a quadratic equation.

4. Here, LHS = (x – 3) (2x + 1) = 2x² – 5x – 3
and RHS = x(x + 5) = x² + 5x.
Hence, (x – 3) (2x + 1) = x(x + 5) can be rewritten as
2x² – 5x – 3 = x² + 5x
∴ x² – 10x – 3 = 0
It is of the form ax² + bx + c = 0.
(a = 1, b = -10, c = -3)
Hence, the given equation is a quadratic equation.

5. Here, LHS = (2x – 1)(x – 3) = 2x² – 7x + 3 and
RHS = (x + 5) (x – 1) = x² + 4x – 5.
Hence, the given equation can be rewritten as
2x² – 7x + 3 = x² + 4x – 5
∴ x² – 11x + 8 = 0
It is of the form ax2 + bx + c = 0.
(a = 1, b = -11, c = 8)
Hence, the given equation is a quadratic equation.

6. Here, RHS = (x – 2)² = x² – 4x + 4
Hence, the given equation can be rewritten as
x² + 3x + 1 = x² – 4x + 4
∴ 7x – 3 = 0
It is not of the form ax² + bx + c = 0.
Hence, the given equation is not a quadratic equation.

7. Here, LHS = (x + 2)³ = x³ + 6x² + 12x + 8 and
RHS = 2x (x² – 1) = 2x³ – 2x.
Hence, the given equation can be rewritten as
x³ + 6x² + 12x + 8 = 2x³ – 2x
∴ -x³ + 6x² + 14x + 8 = 0
It is not of the form ax² + bx + c = 0.
Hence, the given equation is not a quadratic equation.

8. Here, RHS = (x – 2)³ = x³ – 6x² + 12x – 8.
Hence, the given equation can be rewritten as
x³ – 4x² – x + 1 = x³ – 6x² + 12x – 8
2x² – 13x + 9 = 0
It is of the form ax² + bx + c = 0.
(a = 2, b = -13, c = 9)
Hence, the given equation is a quadratic equation.

Question 2.
Represent the following situations in the form of quadratic equations:
1. The area of a rectangular plot is 528 m². The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.
Solution:
Let the breadth (in metres) of the rectangular plot be x.
Then, the length (in metres) of the rectangular plot is 2x + 1.
Area of the rectangular plot = Length × Breadth
∴ 528 = (2x + 1) × x
(∵ Area is given to be 528 m²)
∴ 528 = 2x² + x
∴ 2x² + x – 528 = 0 is the required quadratic equation to find the length (2x + 1 m) and breadth (x m) of the rectangular plot.

2. The product of two consecutive positive integers is 306. We need to find the integers.
Solution:
Let the two consecutive positive integer be x and x + 1.
Then, their product = x(x + 1) = x² + x.
This product is given to be 306.
∴ x² + x = 306
∴ x² + x – 306 = 0 is the required quadratic equation to find the consecutive positive integers x and x + 1.

3. Rohan’s mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find Rohan’s present age.
Solution:
Let Rohan’s present age (in years) be x.
Then, his mother’s present age (in years) = x + 26.
3 years from now, Rohan’s age (in years) will be x + 3 and his mother’s age (in years) will be x + 29.
The product of their ages (in years) 3 years from now is given to be 360.
Hence, (x + 3)(x + 29) = 360
∴ x² + 32x + 87 – 360 = 0
∴ x² + 32x – 273 = 0 is the required quadratic equation to find the present ages (in years) of Rohan (x) and his mother (x + 26).

4. A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
Solution:
Let the usual uniform speed of the train be x km/h.
Now, Time = \(\frac{\text { distance }}{\text { speed }}\)
∴ Time required to cover 480 km distance at usual speed = t₁ = \(\frac{480}{x}\) hours
If the speed is 8 km/hour less, the new speed would be (x – 8) km/hour.
∴ Time required to cover 480 km distance at new speed = t₂ = \(\frac{480}{x-8}\) hours
Now, the time required at new speed is 3 hours more than the usual time.
∴ t₂ = t₁ + 3
∴ \(\frac{480}{x-8}=\frac{480}{x}+3\)
∴ 480x = 480(x – 8) + 3x(x – 8)
(Multiplying by x(x – 8))
∴ 480x = 480x – 3840 + 3x² – 24x
∴ 0 = 3x² – 24x – 3840
∴ x² – 8x – 1280 = 0 is the required quadratic equation to find the usual speed (x km/h) of the train.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.7

Question 1.
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
Solution:
Let the age of Ani be x years and the age of Biju be y years.
Then, from the given,
x – y = 3 ………….(1)
or y – x = 3 ………(2)
Dharam is twice as old as Ani.
∴ Age of Dharam = 2x years
Biju is twice as old as his sister Cathy. Hence, the age of Cathy is half the age of Biju.
∴ Age of Cathy = \(\frac{y}{2}\) years
Naturally, Dharam is older than Cathy by 30 years.
2x – \(\frac{y}{2}\) = 30
∴ 4x – y = 60 ………..(3)
1. We solve equation (1) and equation (3).
Subtracting equation (1) from equation (3),
we get
(4x – y) – (x – y) = 60 – 3
∴ 3x = 57
∴ x = 19
Substituting x = 19 in equation (1), we get
19 – y = 3
∴ 19 – 3 = y
∴ y = 16
Hence, the age of Ani is 19 years and the age of Biju is 16 years.

2. We now solve equation (2) and equation (3). Adding equations (2) and (3), we get
(y – x) + (4x – y) = 3 + 60
∴ 3x = 63
∴ x = 21
Substituting x = 21 in equation (2), we get
∴ y – 21 = 3
∴ y = 24
Hence, the age of Ani is 21 years and the age of Biju is 24 years.
Thus, the ages of Ani and Biju are 19 years and 16 years respectively or 21 years and 24 years respectively.

Question 2.
One says, “Give me a hundred, friend! I shall then become twice as rich as you.” The other replies, “If you give me ten, I shall be six times as rich as you.” Tell me what is the amount of their (respective) capital? (From the Bijaganita of Bhaskara II) [Hint: x + 100 = 2(y – 100), y + 10 = 6(x – 10)].
Solution:
Let the amount with the first person (say A) be ₹ x and the amount with the second person (say B) be ₹ y.
If B gives ₹ 100 to A. then A will have ₹(x + 100) and B will have ₹(y – 100).
Then, from the first condition, we get
x + 100 = 2(y – 100)
∴ x + 100 = 2y – 200
∴ x – 2y = -300 ………..(1)
If A gives ₹ 10 to B, then A will have ₹(x – 10) and B will have ₹(y + 10).
Then, from the second condition, we get
y + 10 = 6(x – 10)
∴ y + 10 = 6x – 60
∴ 10 + 60 = 6x – y
∴ 6x – y = 70 ………..(2)
Multiplying equation (2) by 2, we get
12x – 2y = 140 ………..(3)
Subtracting equation (1) from equation (3),
we get
(12x – 2y) – (x – 2y) = 140 – (-300)
∴ 11x = 440
∴ x = 40
Substituting x = 40 in equation (1), we get
40 – 2y = -300
∴ 40 + 300 = 2y
∴ 2y = 340
∴ y = 170
Thus, the first person has got ₹ 40 and the second person has got ₹ 170.

Question 3.
A train covered a certain distance at a uniform speed. If the train would have. been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Solution:
Let the regular uniform speed of the train be x km/h and regular time taken by the train be y hours. Then, the total distance of the journey = speed × time = xy km.
Now, according to the first information, the new speed = (x + 10) km/h and new time = (y – 2) hours. Then, speed × time = distance gives
(x + 10) (y – 2) = xy
∴ xy – 2x + 10y – 20 = xy
∴ -2x + 10y = 20 …………..(1)
Again, according to the second condition. the new speed = (x – 10) km/h and new time = (y + 3) hours.
Then, (x – 10) (y + 3) = xy
∴ xy + 3x – 10y – 30 = xy
∴ 3x – 10y = 30 …………..(2)
Adding equations (1) and (2), we get
(-2x + 10y) + (3x – 10y) = 20 + 30
∴ x = 50
Substituting x = 50 in equation (1), we get
-2(50) + 10y = 20
∴ -100 + 10y = 20
∴ 10y = 120
∴ y = 12
Now, the total distance covered by the train = xy = 50 × 12 = 600 km.
Thus, the distance covered by the train is 600 km.

Question 4.
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
Solution:
Let the number of students in each row be x and the number of rows be y. Then total number of students = xy.
From the first condition, number of students in each row = x + 3 and the number of rows = y – 1.
∴ (x + 3)(y – 1) = xy
∴ xy – x + 3y – 3 = xy
∴ -x + 3y = 3 …………..(1)
From the second condition, number of students in each row = x – 3 and the number of rows = y + 2.
∴ (x – 3) (y + 2) = xy
∴ xy + 2x – 3y – 6 = xy
∴ 2x – 3y = 6 ……….. (2)
Adding equations (1) and (2), we get
(-x + 3y) + (2x – 3y) = 3 + 6
∴ x = 9
Substituting x = 9 in equation (1), we get
-9 + 3y = 3
∴ 3y = 12
∴ y = 4
Now, total number of students = xy = 9 × 4 = 36. Thus, the number of students in the class is 36.

Question 5.
In a ΔABC, ∠C = 3∠B = 2 (A + B). Find the three angles.
Solution:
In ΔABC, we have
∠A + ∠B + ∠C = 180°
∴ ∠A + ∠B + 3∠B = 180° (∵ ∠C = 3∠B)
∴ ZA + 4∠B = 180° …………..(1)
Again, ∠A + ∠B + ∠C = 180°
∠A + ∠B + 2(∠A + ∠B) = 180° (∵ ∠C = 2 (∠A + ∠B))
∴ 3(∠A + ∠B) = 180°
∴ ∠A + ∠B = 60° ……….(2)
Subtracting equation (2) from equation (1),
we get
(∠A + 4∠B) – (∠A + ∠B) = 180° – 60°
∴ 3∠B = 120°
∴ ∠B = 40°
Substituting ∠B = 40° in equation (2), we get
∠A + 40° = 60°
∴ ∠A = 20°
Substituting ∠B = 40° in ∠C = 3∠B, we get
∠C = 3(40°)
∴ ∠C = 120°
Thus, in ΔABC, ∠A = 20°; ∠B = 40°; ∠C = 120°
Note: Replacing ∠A + ∠B = \(\frac{\angle \mathrm{C}}{2}\) in ∠A + ∠B + ∠C = 180°, we get a simple equation in one variable is \(\frac{3}{2}\)∠C = 180°.
After solving it for ∠C, ∠B and ∠A can be found easily.

Question 6.
Draw the graphs of the equations 5x – y = 5 and 3x – y = 3. Determine the co-ordinates of the vertices of the triangle formed by these lines and the y-axis.
Solution:
5x – y = 5 gives y = 5x – 5

x	1	2
y	0	5

3x – y = 3 gives y = 3x – 3

x	1	2
y	0	3

Now, we draw the graphs of both the equations.

From the graph, we observe that the co-ordinates of the vertices of the triangle formed by the graphs of 5x – y = 5 and 3x – y = 3 and the y-axis are (1, 0), (0, -3) and (0, -5).

Question 7.
Solve the following pair of linear equations:
1. px + qy = p – q
qx – py = p + q
2. ax + by = c
bx + ay = 1 + c
3. \(\frac{x}{a}-\frac{y}{b}=0\)
ax + by = a² + b²
4. (a – b)x + (a + b) y = a² – 2ab – b²
(a + b) (x + y) = a² + b²
5. 152x – 378y = -74
-378x + 152y = -604
Solution:
1. px + qy = p – q ……….(1)
qx – py = p + q ……….(2)
Multiplying equation (1) by p and equation (2) by q, we get
p²x + pqy = p² -pq ……….(3)
q²x – pqy = pq + q² ……….(4)
Adding equations (3) and (4), we get
(p²x + pqy) + (q²x – pqy) = (p² – pq) + (pq + q²)
∴ x(p² + q²) = p² + q²
∴ x = 1
Substituting x = 1 in equation (1), we get
p(1) + qy = p – q
∴ qy = -q
∴ y = -1
Thus, the solution of the given pair of linear equations is x = 1, y = -1.

2. ax + by = c ……….(1)
bx + ay = 1 + c ……….(2)
Multiplying equation (1) by a and equation (2) by b, we get
a²x + aby = ac ……….(3)
b²x + aby = b + bc ……….(4)
Subtracting equation (4) from equation (3), we get
(a²x + aby) – (b²x + aby) = ac – (b + bc)
x(a² – b²) = ac – b – bc
x = \(\frac{c(a-b)-b}{a^2-b^2}\)
Substituting x = \(\frac{c(a-b)-b}{a^2-b^2}\) in equation (1), we get

Thus, the solution of the given pair of linear equations is
x = \(\frac{c(a-b)-b}{a^2-b^2}\), y = \(\frac{c(a-b)+a}{a^2-b^2}\)

3. \(\frac{x}{a}-\frac{y}{b}=0\) ……….(1)
ax + by = a² + b² ……….(2)
From equation (1), we get
\(\frac{x}{a}=\frac{y}{b}\)
y = \(\frac{b}{a}\)x
Substituting y = \(\frac{b}{a}\)x in equation (2), we get

Substituting x = a in y = \(\frac{b}{a}\)x, we get
y = \(\frac{b}{a}\)(a)
∴ y = b
Thus, the solution of the given pair of linear equations is x = a, y = b.

4. (a – b)x + (a + b)y = a² – 2ab – b² ……….(1)
(a + b) (x + y) = a² + b²
∴ (a + b)x + (a + b)y = a² + b² ……….(2)
Subtracting equation (1) from equation (2), we get
[(a + b)x + (a + b)y] – [(a – b)x + (a + b)y] = (a² + b²) – (a² – 2ab – b²)
∴ x(a + b – a + b) = a² + b² – a² + 2ab + b²
∴ x (2b) = 2ab + 2b²
∴ x = \(\frac{2 b(a+b)}{2 b}\)
∴ x = a + b
Substituting x = a + b in equation (1), we get
(a – b)(a + b) + (a + b)y = a² – 2ab – b²
∴ a² – b² + (a + b) y = a² – 2ab – b²
∴ (a + b)y = -2ab
∴ y = \(-\frac{2 a b}{a+b}\)
Thus, the solution of the given pair of linear equations is x = a + b, y = \(-\frac{2 a b}{a+b}\)

5. 152x – 378y = -74 ……….(1)
-378x + 152y = -604 ……….(2)
Adding equations (1) and (2), we get
-226x – 226y = -678
∴ x + y = 3 (Dividing by -226) ……….(3)
Subtracting equation (2) from equation (1),
we get
(152x – 378y) – (-378x + 152y) = (-74) – (-604)
∴ 530x – 530y = 530
x – y = 1 (Dividing by 530) ……….(4)
Adding equations (3) and (4), we get
2x = 4
∴ x = 2
Substituting x = 2 in equation (3), we get 2 + y = 3
∴ y = 1
Thus, the solution of the given pair of linear equations is x = 2, y = 1.

Question 8.
ABCD is a cyclic quadrilateral (See the given figure). Find the angles of the cyclic quadrilateral.

Solution:
ABCD is a cyclic quadrilateral.
∠A + ∠C = 180° and ∠B + ∠D = 180°
∠A + ∠C = 180° gives 4y + 20° – 4x = 180°
∴ 4y – 4x = 160
∴ y – x = 40° (Dividing by 4) …………..(1)
∠B + ∠D = 180° gives 3y – 5° – 7x + 5° = 180°
∴ 3y – 7x = 180° …………..(2)
From equation (1), we get y = x + 40°
Substituting y = x + 40° in equation (2), we get
3(x + 40°) – 7x = 180°
∴ 3x + 120° – 7x = 180°
∴ -4x = 60°
∴ x = -15°
Substituting x = -15° in equation (1), we get
y – (-15) = 40°
∴ y + 15° = 40°
∴ y = 25°
Now, ∠A = 4y + 20° = 4(25°) + 20° = 120°,
∠B = 3y – 5° = 3 (25°) – 5° = 70°,
∠C = -4x = -4(-15) = 60° and
∠D = -7x + 5° = -7(-15°) + 5° = 110°
Thus, in the given cyclic quadrilateral ABCD.
∠A = 120°, ∠B = 70°, ∠C = 60°, ∠D = 110°.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.6

Question 1.
Sovle the following pairs of equations by reducing them to a pair of linear equations:

Solution:
1. The given pair of equations is

Taking \(\frac{1}{x}=a\) and \(\frac{1}{y}=b\) in both the equations, we get
\(\frac{1}{2}\)a + \(\frac{1}{3}\)b = 2 ……….(3)
\(\frac{1}{3}\)a + \(\frac{1}{2}\)b = \(\frac{13}{6}\) ………..(4)
Multiplying both the equations by 6, we get
3a + 2b = 12 ……(5)
2a + 3b = 13 ……(6)
Adding equations (5) and (6), we get
5a + 5b = 25
∴ a + b = 5 ……….(7)
Subtracting equation (6) from equation (5), we get
a – b = -1 ………..(8)
Equations (7) and (8) can be solved easily to get a = 2 and b = 3.
Then a = \(\frac{1}{x}\) = 2 and b = \(\frac{1}{y}\) = 3
∴ x = \(\frac{1}{2}\) and y = \(\frac{1}{3}\)
Thus, the solution of the given pair of equations is x = \(\frac{1}{2}\), y = \(\frac{1}{3}\)

2. The given pair of equations is
\(\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}=2\) ……….(1)
\(\frac{4}{\sqrt{x}}-\frac{9}{\sqrt{y}}=-1\) ……….(2)
Taking \(\frac{1}{\sqrt{x}}=a\) and \(\frac{1}{\sqrt{y}}=b\) in both the equations, we get
2a + 3b = 2 ……….(3)
4a – 9b = -1 ……….(4)
Multiplying equation (3) by 3, we get
6a + 9b = 6 ……….(5)
Adding equations (4) and (5). we get
(4a – 9b) + (6a + 9b) = -1 + 6
∴ 10a = 5
∴ a = \(\frac{1}{2}\)
Substituting a = \(\frac{1}{2}\) in equation (3), we get
2(\(\frac{1}{2}\)) + 3b = 2
∴ 1 + 3b = 2
∴ 3b = 1
∴ b = \(\frac{1}{3}\)
Now, a = \(\frac{1}{\sqrt{x}}=\frac{1}{2}\)
∴ 2 = \(\sqrt{x}\)
∴ x = 4
Again b = \(\frac{1}{\sqrt{y}}=\frac{1}{3}\)
∴ 3 = \(\sqrt{y}\)
∴ y = 9
Thus, the solution of the given pair of equations is x = 4, y = 9,

3. The given pair of equations is
\(\frac{4}{x}\) + 3y = 14 ……….(1)
\(\frac{3}{x}\) – 4y = 23 ……….(2)
Taking \(\frac{1}{x}\) = a in both the equations, we get
4a + 3y = 14 ……….(3)
3a – 4y = 23 ……….(4)
Multiplying equation (3) by 4 and equation (4) by 3 and adding them, we get
4(4a + 3y) + 3(3a – 4y) = 4(14) + 3(23)
∴ 16a + 12y + 9a – 12y = 56 + 69
∴ 25a = 125
∴ a = 5
Now, a = \(\frac{1}{x}\) = 5
∴ x = \(\frac{1}{5}\)
Substituting x = \(\frac{1}{5}\) in equation (1), we get
\(\frac{4}{\frac{1}{5}}\) + 3y = 14
∴ 20 + 3y = 14
∴ 3y = -6
∴ y = -2
Thus, the solution of the given pair of equations is x = \(\frac{1}{5}\), y = -2.

4. The given pair of equations is
\(\frac{5}{x-1}+\frac{1}{y-2}=2\) ………..(1)
\(\frac{6}{x-1}-\frac{3}{y-2}=1\) …………(2)
Taking \(\frac{1}{x-1}=a\) and \(\frac{1}{y-2}=b\) in both the equations, we get
5a + b = 2 ………..(3)
6a – 3b = 1 ………..(4)
Multiplying equation (3) by 3 and then additing equation (4) to it, we get
3(5a + b) + (6a – 3b) = 3(2) + 1
∴ 15a + 3b + 6a – 3b = 6 + 1
∴ 21a = 7
a = \(\frac{1}{3}\)
Substituting a = \(\frac{1}{3}\) in equation (4), we get
6(\(\frac{1}{3}\)) – 3b = -1
∴ 2 – 3b = 1
∴ 1 = 3b
∴ b = \(\frac{1}{3}\)
Now, a = \(\frac{1}{x-1}=\frac{1}{3}\)
∴ x – 1 = 3
∴ x = 4
Again, b = \(\frac{1}{y-2}=\frac{1}{3}\)
∴ y – 2 = 3
∴ y = 5
Thus, the solution of the given pair of equations is x = 4, y = 5.

5. The given pair of equations is \(\frac{7 x-2 y}{x y}=5\) and \(\frac{8 x+7 y}{x y}=15\)
Hence, \(\frac{7}{y}-\frac{2}{x}=5\) ………..(1)
and \(\frac{8}{y}+\frac{7}{x}=15\) ………..(2)
Taking \(\frac{1}{y}\) = a and \(\frac{1}{y}\) = b in both the equations, we get
7a – 2b = 5 ………..(3)
8a + 7b = 15 ………..(4)
Expressing the equation in the standard form, we get
7a – 2b – 5 = 0 and 8a + 7b – 15 = 0

Now, a = \(\frac{1}{y}\) = 1 ∴ y = 1
and b = \(\frac{1}{x}\) = 1 ∴ x = 1
Thus, the solution of the given pair of equations is x = 1, y = 1.

6. The given pair of equations is 6x + 3y = 6xy and 2x + 4y = 5xy
Dividing both the equations by xy, we get
\(\frac{6}{y}+\frac{3}{x}=6\) ………..(1)
\(\frac{2}{y}+\frac{4}{x}=5\) ………..(2)
Taking \(\frac{1}{y}\) = a and \(\frac{1}{x}\) = b,
we get
6a + 3b = 6
i.e., 2a + b = 2 ……(3)
2a + 4b = 5 ……(4)
Subtracting equation (3) from equation (4),
we get
(2a + 4b) – (2a + b) = 5 – 2
∴ 3b = 3
∴ b = 1
Substituting b = 1 in equation (3), we get
2a + 1 = 2
∴ 2a = 1
∴ a = \(\frac{1}{2}\)
Now, a = \(\frac{1}{y}=\frac{1}{2}\) ∴ y = 2
and b = \(\frac{1}{x}\) = 1 ∴ x = 1
Thus, the solution of the given pair of equations is x = 1, y = 2.

7. The given pair of equations is
\(\frac{10}{x+y}+\frac{2}{x-y}=4\) ………..(1)
\(\frac{15}{x+y}-\frac{5}{x-y}=-2\) ………..(2)
Taking \(\frac{1}{x+y}=a\) and \(\frac{1}{x-y}=b\) in both the equations, we get
10a + 2b = 4
i.e., 5a + b = 2 ……(3)
15a – 5b = -2 ……(4)
Multiplying equation (3) by 5 and then adding equation (4) to it, we get
5(5a + b) + (15a – 5b) = 5(2) + (-2)
∴ 25a + 5b + 15a – 5b = 10 – 2
∴ 40a = 8
∴ a = \(\frac{1}{5}\)
Substituting a = \(\frac{1}{5}\) in equation (3), we get
5(\(\frac{1}{5}\)) + b = 2
∴ 1 + b = 2
∴ b = 1
Now, a = \(a=\frac{1}{x+y}=\frac{1}{5}\)
∴ x + y = 5 ……(5)
and b = \(\frac{1}{x-y}=1\)
∴ x – y = 1 ………(6)
Adding equations (5) and (6), we get
2x = 6
∴ x = 3
Substituting x = 3 in equations (5), we get
3 + y = 5
∴ y = 2
Thus, the solution of the given pair of equations is x = 3, y = 2.

8. The given pair of equations is
\(\frac{1}{3 x+y}+\frac{1}{3 x-y}=\frac{3}{4}\) ………(1)
\(\frac{1}{2(3 x+y)}-\frac{1}{2(3 x-y)}=-\frac{1}{8}\) ………(2)
Taking \(\frac{1}{3 x+y}=a\) and \(\frac{1}{3 x-y}=b\) in both the equations, we get
a + b = \(\frac{3}{4}\) ………(3)
\(\frac{a}{2}-\frac{b}{2}=-\frac{1}{8}\)
i.e., a – b = –\(\frac{2}{8}\)
i.e., a – b = –\(\frac{1}{4}\) ………….(4)
Adding equations (3) and (4), we get
2a = \(\frac{2}{4}\)
∴ a = \(\frac{1}{4}\)
Substituting a = \(\frac{1}{4}\) in equation (3), we get
\(\frac{1}{4}+b=\frac{3}{4}\)
∴ b = \(\frac{1}{2}\)
Now, a = \(\frac{1}{3 x+y}=\frac{1}{4}\)
3x + y = 4 ………….(5)
and b = \(\frac{1}{3 x-y}=\frac{1}{2}\)
∴ 3x – y = 2 ………….(6)
Adding equations (5) and (6), we get
6x = 6
∴ x = 1
Substituting x = 1 in equations (5), we get
3(1) + y = 4
∴ y = 1
Thus, the solution of the given pair of equations is x = 1, y = 1.

2. Formulate the following problems as a pair of equations, and hence find their solutions:

Question 1.
Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
Solution:
Let Ritu’s speed of rowing in still water be x km/h and the speed of the current by y km/h.
Then, her net speed going down-stream = (x + y) km/h and her net speed going upstream = (x – y) km/h.
Also, time = \(\frac{\text { distance }}{\text { speed }}\)
Then, form the first condition, we get
2 = \(\frac{20}{x+y}\)
∴ x + y = 10 ……(1)
And, from the second condition, we get
2 = \(\frac{4}{x-y}\)
∴ x – y = 2 ………..(2)
Adding equations (1) and (2), we get
2x = 12
∴ x = 6
Substituting x = 6 in equation (1), we get
6 + y = 10
∴ y = 4
Thus, Ritu’s speed of rowing in still water is 6 km/h and the speed of the current is 4 km/h.

Question 2.
2 women and 5 men can together finish an embroidery work in 4 days. while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
Solution:
Suppose that 1 woman alone can finish the work in x days and 1 man alone can finish the work in y days.
∴ Work done by 1 woman in 1 day = \(\frac{1}{x}\) part and work done by 1 man in 1 day \(\frac{1}{y}\) part.
Then, work done by 2 women and 5 men together in 1 day = \(\left(\frac{2}{x}+\frac{5}{y}\right)\) part.
But, according to the first information given, 2 women and 5 men together finish the work in 4 days, i.e., in one day they can finish \(\frac{1}{4}\) part of the work.
Hence, we get the following equation:
\(\frac{2}{x}+\frac{5}{y}=\frac{1}{4}\) ……(1)
Similarly, from the second information given, we get
\(\frac{3}{x}+\frac{6}{y}=\frac{1}{3}\) ……(2)
Taking \(\frac{1}{x}\) = a and \(\frac{1}{y}\) = b in both the equations, we get
2a + 5b = \(\frac{1}{4}\) ……(3)
3a + 6b = \(\frac{1}{3}\) ……(4)
Multiplying equation (3) by 6 and equation (4) by 5, we get
12a + 30b = \(\frac{6}{4}\) ……(5)
15a + 30b = \(\frac{5}{3}\) ……(6)
Subtracting equation (5) from equation (6), we get
(15a + 30b) – (12a + 30b) = \(\frac{5}{3}-\frac{6}{4}\)
15a + 30b – 12a – 30b = \(\frac{20-18}{12}\)
∴ 3a = \(\frac{2}{12}\)
∴ a = \(\frac{1}{18}\)
Substituting a = \(\frac{1}{18}\) in equation (3), we get
2(\(\frac{1}{18}\)) + 5b = 4
∴ 5b = \(\frac{1}{4}-\frac{1}{9}\)
∴ 5b = \(\frac{5}{36}\)
∴ b = \(\frac{1}{36}\)
Now, a = \(\frac{1}{x}=\frac{1}{18}\) ∴ x = 18
and b = \(\frac{1}{y}=\frac{1}{36}\) ∴ y = 36
Thus, 1 woman alone can finish the work in 18 days and 1 man alone can finish the work in 36 days.

Question 3.
Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Solution:
Let the speed of the train be x km/h and the speed of the bus be y km/h.
Also, time = \(\frac{\text { distance }}{\text { speed }}\)
In the first case, she travels 60 km by train and the remaining 240 km (300 – 60) by bus.
∴ Time taken for journey by train = \(\frac{60}{x}\)h and time taken for journey by bus \(\frac{240}{y}\)h.
∴ Total time taken = \(\left(\frac{60}{x}+\frac{240}{y}\right)\)h
In the first case, total time taken = 4 h.
Hence, we get the following equation:
\(\frac{60}{x}+\frac{240}{y}=4\) ………..(1)
Similarly, in the second case, the distances she travels by train and bus are 100 km and 200 km respectively and time taken by those journies are \(\frac{100}{x}\)h and \(\frac{200}{y}\)h respectively.
In this case, the total time taken = 4 hours + 10 minutes = 4\(\frac{1}{6}\) hours.
Hence, we get the following equation:
\(\frac{100}{x}+\frac{200}{y}=4 \frac{1}{6}\)
∴ \(\frac{100}{x}+\frac{200}{y}=\frac{25}{6}\) ………..(2)
Taking \(\frac{1}{x}\) = a and \(\frac{1}{y}\) = b in both the equations, we get
60a + 240b = 4 ………..(3)
100a + 200b = \(\frac{25}{6}\) ………..(4)
Multiplying equation (3) by 5 and equation (4) by 6, we get
300a + 1200b = 20 ………..(5)
600a + 1200b = 25 ………..(6)
Subtracting equation (5) from equation (6), we get
(600a + 1200b) – (300a + 1200b) = 25 – 20
∴ 300a = 5
∴ a = \(\frac{1}{60}\)
Substituting a = \(\frac{1}{60}\) in (3), we get
60(\(\frac{1}{60}\)) + 240b = 4
∴ 1 + 240b = 4
∴ 240b = 3
∴ b = \(\frac{1}{80}\)
Now, a = \(\frac{1}{x}\) = \(\frac{1}{60}\)
∴ x = 60
and b = \(\frac{1}{y}\) = \(\frac{1}{80}\)
∴ y = 80
Thus, the speed of the train is 60 km/h and the speed of the bus is 80 km/h.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.5

Question 1.
Which of the following pairs of linear equations has a unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross-multiplication method:
1. x – 3y – 3 = 0
3x – 9y – 2 = 0
2. 2x + y = 5
3x + 2y = 8
3. 3x – 5y = 20
6x – 10y = 40
4. x – 3y – 7 = 0
3x – 3y – 15 = 0
Solution:
1. x – 3y – 3 = 0 and 3x – 9y – 2 = 0
Here, a₁ = 1; a₂ = 3; b₁ = -3; b₂ = -9; c₁ = -3 and c₂ = -2.
Now, \(\frac{a_1}{a_2}=\frac{1}{3}, \quad \frac{b_1}{b_2}=\frac{-3}{-9}=\frac{1}{3}\) and \(\frac{c_1}{c_2}=\frac{-3}{-2}=\frac{3}{2}\)
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Hence, the given pair of linear equations has no solution.

2. 2x + y – 5 = 0 and 3x + 2y – 8 = 0
Here, a₁ = 2; a₂ = 3; b₁ = 1; b₂ = 2; c₁ = -5 and c₂ = -8.
Now, \(\frac{a_1}{a_2}=\frac{2}{3}, \quad \frac{b_1}{b_2}=\frac{1}{2}\) and \(\frac{c_1}{c_2}=\frac{-5}{-8}=\frac{5}{8}\)
Here, \(\frac{1}{2}\)
Hence, the given pair of linear equations has a unique solution.
Now,


Thus, the unique solution of the given pair of linear equations is x = 2, y = 1.

3. 3x – 5y – 20 = 0 and 6x – 10y – 40 = 0
Here, a₁ = 3, a₂ = 6, b₁ = -5, b₂ = -10, c₁ = -20 and c₂ = -40.
Now, \(\frac{a_1}{a_2}=\frac{3}{6}=\frac{1}{2}\), \(\frac{b_1}{b_2}=\frac{-5}{-10}=\frac{1}{2}\) and \(\frac{c_1}{c_2}=\frac{-20}{-40}=\frac{1}{2}\)
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Hence, the given pair of linear equations has infinitely many solutions.

4. x – 3y – 7 = 0 and 3x – 3y – 15 = 0
Here, a₁ = 1, a₂ = 3, b₁ = -3, b₂ = -3, c₁ = -7 and c₂ = -15.
Now, \(\frac{a_1}{a_2}=\frac{1}{3}, \frac{b_1}{b_2}=\frac{-3}{-3}=1\) and \(\frac{c_1}{c_2}=\frac{-7}{-15}=\frac{7}{15}\)
Here, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
Hence, the given pair of linear equations has a unique solution.
Now,

Thus, the unique solution of the given pair of linear equations is x = 4, y = -1.

Question 2.
1. For which values of a and b does the following pair of linear equations have an infinite number of solutions?
2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
2. For which value of k will the following pair of linear equations have no solution ?
3x + y = 1
(2k – 1)x + (k – 1) y = 2k + 1
Solution:
1. For the given pair of equations, we express them in the standard form as:
2x + 3y – 7 = 0 and
(a – b)x + (a + b)y – (3a + b – 2) = 0
Here, A₁ = 2; A₂ = a – b; B₁ = 3; B₂ = a + b; C₁ = -7 and C₂ = -(3a + b – 2)
Then, \(\frac{\mathrm{A}_1}{\mathrm{~A}_2}=\frac{2}{a-b}, \frac{\mathrm{B}_1}{\mathrm{~B}_2}=\frac{3}{a+b}\) and \(\frac{C_1}{C_2}=\frac{-7}{-(3 a+b-2)}=\frac{7}{3 a+b-2}\)
For the pair of equations to have infinite number of solution, we must have

∴ 2(a + b) = 3(a – b)
∴ 2a + 2b = 3a – 3b
∴ 5b = a
∴ a = 5b ………..(1)
Again, \(\frac{3}{a+b}=\frac{7}{3 a+b-2}\)
∴ 3 (3a + b – 2) = 7(a + b)
∴ 9a + 3b – 6 = 7a + 7b
∴ 2a – 4b = 6
∴ 2 (5b) – 4b = 6 [from (1), a = 5b]
∴ 6b = 6
∴ b = 1
Now, a = 5b
∴ a = 5(1)
∴ a = 5
Thus, for a = 5 and b = 1, the given pair of linear equations will have an infinite number of solutions.

2. We express the given equations in the standard form as:
3x + y – 1 = 0 and
(2k – 1)x + (k – 1)y – (2k + 1) = 0.
Here, a₁ = 3; a₂ = 2k – 1; b₁ = 1; b₂ = k – 1; c₁ = -1 and c₂ = -(2k + 1).
Then, \(\frac{a_1}{a_2}=\frac{3}{2 k-1}, \quad \frac{b_1}{b_2}=\frac{1}{k-1}\) and \(\frac{c_1}{c_2}=\frac{-1}{-(2 k+1)}=\frac{1}{2 k+1}\)
For the pair of equations to have not solution, we must have
\(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
∴ \(\frac{3}{2 k-1}=\frac{1}{k-1} \neq \frac{1}{2 k+1}\)
\(\frac{3}{2 k-1}=\frac{1}{k-1}\)
∴ 3(k – 1) = 2k – 1
∴ 3k – 3 = 2k – 1
∴ k = 2
For k = 2.
\(\frac{a_1}{a_2}=\frac{3}{2(2)-1}=1\), \(\frac{b_1}{b_2}=\frac{1}{2-1}=1\) and \(\frac{c_1}{c_2}=\frac{1}{2(2)+1}=\frac{1}{5}\)
Thus, k = 2 satisfies \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Thus, for k = 2, the given pair of linear equations has no solution.

Question 3.
Solve the following pair of linear equations by the substitution and cross-multiplication methods:
8x + 5y = 9
3x + 2y = 4
Solution:
1. Substitution method:
8x + 5y = 9 ……….(1)
3x + 2y = 4 ……….(2)
From equation (2), we get y = \(\frac{4-3 x}{2}\)
Substituting y = \(\frac{4-3 x}{2}\) in equation (1).
we get
8x + 5(\(\frac{4-3 x}{2}\)) = 9
∴ 16x + 5(4 – 3x) = 18 (Multiplying by 2)
∴ 16x + 20 – 15x = 18
∴ x = -2
Substituting x = -2 in y = \(\frac{4-3 x}{2}\), we get
∴ y = \(\frac{4-3(-2)}{2}\)
∴ y = 5
Thus, the solution of the given pair of linear equations is x = -2, y = 5.

2. Cross-multiplication method:
We express both the equations in the standard form as:
8x + 5y – 9 = 0 and 3x + 2y – 4 = 0
Here, a₁ = 8; b₁ = 5; c₁ = -9; a₂ = 3; b₂ = 2 and c₂ = -4.
Now, we arrange the coefficients as required in cross-multiplication method as:

Thus, the solution of the given pair of linear equations is x = -2, y = 5.

4. Form the pair of linear equations in the following problems and find their solutions. (if they exist) by any algebraic method:

Question 1.
A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days she has to pay ₹ 1000 as hostel charges whereas a student B, who takes food for 26 days, pays ₹ 1180 as hostel charges. Find the fixed charges and the cost of food per day.
Solution:
Let the fixed monthly charge be ₹ x and the cost of food per day be ₹ y.
Then, from the give data, we get the following pair of linear equations:
x + 20y = 1000 ……….(1)
x + 26y = 1180 ………..(2)
These equations in standard form are:
x + 20y – 1000 = 0 ……….(3)
x + 26y – 1180 = 0 ……….(4)
Now, we solve the equation by cross-multiplication method.

Thus, monthly fixed charge is ₹ 400 and the cost of food per day is ₹ 30.
Note: Here, the elimination method would be much easter, but we have solved. it by cross-multiplication method to show more applications of that method.

Question 2.
A fraction becomes \(\frac{1}{3}\) when 1 is subtracted from the numerator and it becomes \(\frac{1}{4}\) when 8 is added to its denominator. Find the fraction.
Solution:
Let the numerator and the denominator of the required fraction be x and y respectively.
Then, the required fraction = \(\frac{x}{y}\)
By the given data, we get
\(\frac{x-1}{y}=\frac{1}{3}\)
∴ 3x – 3 = y
∴ 3x – y = 3 ……….(1)
Also, \(\frac{x}{y+8}=\frac{1}{4}\)
∴ 4x = y +8
∴ 4x – y = 8 …………(2)
Subtracting equation (1) from equation (2),
we get
(4x – y) – (3x – y) = 8 – 3
∴ 4x – y – 3x + y = 5
∴ x = 5
Substituting x = 5 in equation (1),
we get
3(5) – y = 3
∴ 15 – 3 = y
∴ y = 12
Hence, the required fraction = \(\frac{x}{y}=\frac{5}{12}\)

Question 3.
Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?
Solution:
Suppose Yash gave x right answers and y wrong answers.
Then, from the given data, we get
3x – y = 40 ………(1)
and 4x – 2y = 50, i.e.. 2x – y = 25 ……….(2)
We express the equations in the standard form as
3x – y – 40 = 0 ………(3)
2x – y – 25 = 0 ………(4)
Then,

Then, the total number of questions in the test = x + y = 15 + 5 = 20.
Thus, there were 20 questions in the test.

Question 4.
Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?
Solution:
Let the speed of the car starting from A be x km/hour and the speed of the car starting from B be y km/hour such that x > y. If the cars travel in the same direction and meet, they should be travelling in the direction from A towards B as the car starting from A is faster than the car starting from B.

Suppose the cars meet at place P after 5 hours, when they travel in the same direction. Then, the distance travelled in 5 hours by the car starting from A= 5x km = AP (Distance = Speed × Time) Similarly, the distance travelled in 5 hours by the car starting from B = 5y km = BP.
Now, AB = 100 km
∴ AP – BP = 100
∴ 5x – 5y = 100
∴ x – y = 20 (Dividing by 5) ………(1)

Suppose the cars meet at place Q after 1 hour when they travel in opposite directions.
Then, distance travelled in 1 hour by the car starting from A = x km = AQ
Similarly, distance travelled in 1 hour by the car starting from B = y km = BQ.
Now, AB = 100 km
∴ AQ + BQ = 100
∴ x + y = 100 ………(2)
Adding equations (1) and (2), we get
(x – y) + (x + y) = 20 + 100
∴ 2x = 120
∴ x = 60
Substituting x = 60 in equation (2), we get
60 + y = 100
∴ y = 40
Thus, the speeds of the cars starting from A and B are 60 km/hour and 40 km/hour respectively under the assumption that x > y.

Question 5.
The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.
Solution:
Let the length of the rectangle be x units and its breadth be units.
Area of a rectangle = Length × Breadth
∴ Area of given rectangle = xy square units
According to the first condition given,
new reduced length = (x – 5) units,
new increased breadth = (y + 3) units and new reduced area = (xy – 9) square units.
Then, Length × Breadth = Area of a rectangle gives
(x – 5) (y + 3) = xy – 9
∴ xy + 3x – 5y – 15 = xy – 9
∴ 3x – 5y – 6 = 0 ……….(1)
Similarly, from the second condition given,
new increased length = (x + 3) units.
new increased breadth = (y + 2) units and
new increased area = (xy + 67) square units.
Again, Length × Breadth = Area of a rectangle gives
(x + 3)(y + 2) = xy + 67
∴ xy + 2x + 3y + 6 = xy + 67
∴ 2x + 3y – 61 = 0 ………..(2)
We solve these equations (1) and (2) by cross-multiplication method.


∴ x = \(\frac{323}{19}\) and y = \(\frac{171}{19}\)
∴ x = 17 and y = 9
Thus, the length and the breadth of the given rectangle are 17 units and 9 units respectively.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 Triangles Ex 6.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 6 Triangles Exercise 6.4

Question 1.
Let ΔABC ~ ΔDEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.
Solution :
ΔABC ~ ΔDEF

Question 2.
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Solution :

In trapezium ABCD, AB || CD and diagonals AC and BD intersect at O.
Then, in ΔAOB and ΔCOD.
∠OAB = ∠OCD (Alternate angles)
∠OBA = ∠ODC (Alternate angles)
∠AOB = ∠COD (Vertically opposite angles)
∴ By AAA criterion, ΔAOB ~ ΔCOD.

Question 3.
In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar (ABC) / ar (DBC) = \(\frac{AO}{DO}\)
Solution :

Draw AM ⊥ BC and DN ⊥ BC.
Then, ar (ABC) = \(\frac{1}{2}\) × BC × AM and
ar (DBC) = \(\frac{1}{2}\) × BC × DN

In ΔAMO and ΔDNO
∠AMO = ∠DNO (Right angles)
∠AOM = ∠DON (Vertically opposite angles)
∴ By AA criterion, ΔAMO ~ ΔDNO.
∴ \(\frac{AM}{DN}=\frac{AO}{DO}\) ……………….(2)
From (1) and (2), ar (ABC) / ar (DBC) = \(\frac{AO}{DO}\)

Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution :
Given: ΔABC ~ ΔPQR and ar (ABC) = ar (PQR)
To prove : ΔABC ≅ ΔPQR

Proof: ΔABC ~ ΔPQR

∴ AB = PQ, BC = QR and CA = RP
∴ By SSS criterion for congruence of triangles, ΔABC = ΔPOR.

Question 5.
D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
Solution :

In ΔABC, D, E and F are the mid-points of sides AB, BC and CA respectively.
Then, EF || AB and DE || AC
∴ EF || AD and DE || AF
∴ ADEF is a parallelogram.
∴ ∠A = ΔDEF
(Opposite angles of parallelogram)
Similarly, we can prove that ∠B = ∠EFD and ∠C = ∠EDF
Now, in ΔABC and ΔEFD,
∠A = ∠E, ∠B = ∠F and ∠C = ∠D
∴ By AAA criterion, ΔABC ~ ΔEFD.
∴ ar (DEF) / ar(ABC) = (\(\frac{EF}{AB}\))² ………………(1)
In ΔABC, E and F are the mid-points of BC and CA respectively.
∴ EF = \(\frac{1}{2}\)AB ………………(2)
(Alternately: ADEF is a parallelogram.
∴ EF = AD = \(\frac{1}{2}\)AB)
From (1) and (2),

Question 6.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution :
Given: ΔABC ~ ΔPQR, AD and PM are medians of triangles ABC and PQR respectively.

Proof :
In ΔABC, AD is a median ∴ BD = \(\frac{1}{2}\)BC
In ΔPQR, PM is a median ∴ QM = \(\frac{1}{2}\)QR.
ΔABC ~ ΔPQR
∴ ∠B = ∠Q and \(\frac{AB}{PQ}=\frac{BC}{QR}\)
∴ ∠ABD = ∠PQM and \(\frac{AB}{PQ}=\frac{BD}{QM}\)
So, by SAS criterion ΔABD ~ ΔPQM.
∴ \(\frac{AB}{PQ}=\frac{AD}{PM}\) ……………(1)
Now, ΔABC ~ ΔPQR
∴ ar (ABC) / ar (PQR) = (\(\frac{AB}{PQ}\))²
∴ ar (ABC) / ar (PQR) = (\(\frac{AD}{PM}\))² [By (1)]

Question 7.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of an equilateral triangle described on one of its diagonals.
Solution :

ABCD is a square. PAB, is an equilateral triangle described on side AB and QAC is an equilateral triangle described on diagonal AC.
In ΔABC, ∠B = 90° and AB = BC (Properties of a square)
Then, AC² = AB² + BC² (Pythagoras theorem)
∴ AC² = AB² + AB²
∴ AC² = 2AB²
∴ \(\frac{\mathrm{AB}^2}{\mathrm{AC}^2}\) = \(\frac{1}{2}\)
∴ (\(\frac{18}{36}\))
ΔPAB is an equilateral triangle.
∴ ∠P = ∠A = ∠B = ∠60°
ΔQAC is an equilateral triangle.
∴ ∠Q = ∠A = ∠C = 60°
Thus, in ΔPAB and ΔQAC,
∠P = ∠Q and ∠A = ∠A and ∠B = ∠C
∴ By AAA criterion, ΔPAB ~ ΔQAC.
∴ ar (PAB) / ar(QAC) = (\(\frac{AB}{AC}\))²
∴ ar (PAB) / ar(QAC) = \(\frac{1}{2}\) [By (1)]
∴ ar (PAB) = \(\frac{1}{2}\)ar (QAC)
Thus, the area of an equilateral triangle described on a side of a square is half the area of an equilateral triangle described on one of its diagonals.

Tick the correct answer and justify:

Question 8.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
Solution :
The correct answer is (C) 4 : 1.
ΔABC and ΔBDE are equilateral triangles.
Hence, any of their correspondences is a similarity.

Question 9.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
Solution :
The correct answer is (D) 16 : 81.
By theorem 6.6.
Ratio of areas of two similar triangles
= (Ratio of their corresponding sides)²
= (4 : 9)²
= (\(\frac{4}{9}\))²
= 16 : 81