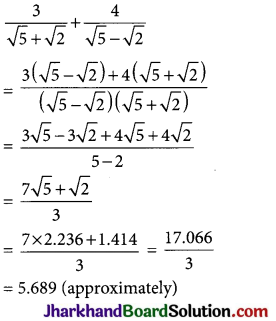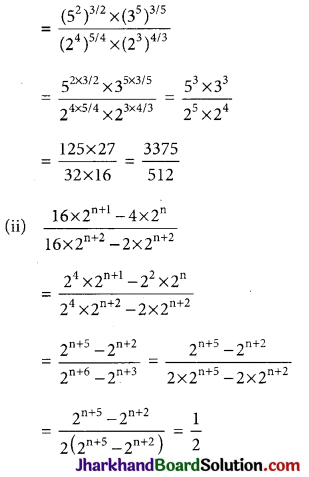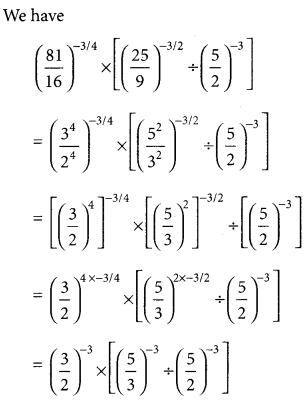Jharkhand Board JAC Class 10 Sanskrit Solutions व्याकरणम् अव्ययपदानि Questions and Answers, Notes Pdf.
JAC Board Class 10th Sanskrit व्याकरणम् अव्ययपदानि
संस्कृतभाषायां शब्दप्रकारद्वयमस्ति – विकारी अविकारी च। ये शब्दः विभक्तिप्रत्यय-उपसर्गः मिलित्वा रूपपरिवर्तनं कुर्वन्ति ते ‘विकारी’ इति शब्देन निर्दिश्यन्ते। अविकारिणः तु कदापि रूपपरिवर्तनं न कुर्वन्ति। एते ‘अव्यय’-शब्देन कथ्यन्ते। अर्थात् येषु शब्देषु लिङ्गवचनकारकादि-सम्बन्धेन रूपपरिवर्तनां न भवति ते अव्ययानि सन्ति। उक्तं च-(संस्कृत भाषा में शब्द के दो प्रकार हैं- विकारी और अविकारी। जो शब्द विभक्ति-प्रत्यय-उपसर्ग से मिलकर रूप परिवर्तन करते हैं वे ‘विकारी’ इस शब्द से निर्देशित किये जाते हैं। अविकारी तो कभी भी रूप परिवर्तन नहीं करते हैं। ये अव्यय शब्द कहे जाते हैं। अर्थात् इन शब्दों में लिङ्ग, वचन, कारक आदि के सम्बन्ध से रूप परिवर्तन नहीं होता है, वे अव्यय पद हैं। जैसा कि कहा है-)
सदृशं त्रिषु लिङ्गेषु सर्वासु स विभक्तिषु।
वचनेषु च सर्वेषु यन्त्र व्येति तदव्ययम्।।
अव्ययानां अन्ते आगतानां र-स्-वर्णानां स्थाने विसर्गः प्रयुज्यते यथा-उच्चैस-उच्चैः, नीचैस नीचैः, अन्तर=अन्त: पुनर-पुनः इति। (अव्ययों के अन्त में आये हुए ‘र’ और ‘स्’ वर्गों के स्थान पर विसर्ग प्रयुक्त किया जाता है जैसे-उच्चैस्-उच्चैः, नीचैस्-नीचैः, अन्तर्-अन्तः, पुनर्=पुनः आदि।)

अव्ययानामपि प्रकार द्वयमस्ति – प्रथमं तावत् रूढ़म्, अव्युत्पन्न वा। यथा-च, वा, विना, पृथगादीनि धातोः अव्युत्पन्नानि। द्वितीयं यौगिकं व्युत्पन्नं वा। यथा पठित्वा, पठितुमादीनि धातोः व्युत्पन्नानि कृदन्दताव्ययानि। सर्वदा, चतुर्धादीनि नाम्न: व्युत्पन्नानि तद्विताव्ययानि च। तद्धिताव्ययानां भेदा अपि सन्ति। यथा- (अव्ययों के दो प्रकार हैं- पहला अधिकार रूढम् अथवा अव्युत्पन्नम् है। जैसे- च, वा, विना, पृथगादीनि धातु से अव्युत्पन्न हैं। दूसरा अधिकार यौगिक अथवा व्युत्पन्न है। पठितुम् आदि धातु से व्युत्पन्न कृदन्त अव्यय हैं। और सर्वदा, चतुर्धा आदि नाम से व्युत्पन्न तद्धित अव्यय हैं। तद्धित अव्ययों के भेद भी हैं। जैसे-)
विभक्ति बोधकानि – कुतः, ग्रामतः, कुत्र अत्रादीनि।
कालबोधकानि – यदा, कदा, सर्वदादीनि।
प्रकारबोधकानि – यथा, तथा, कथम्, इत्थम्, द्वेधादीनि।
विविधानि – अनेकशः पञ्चत्व आदीनि।
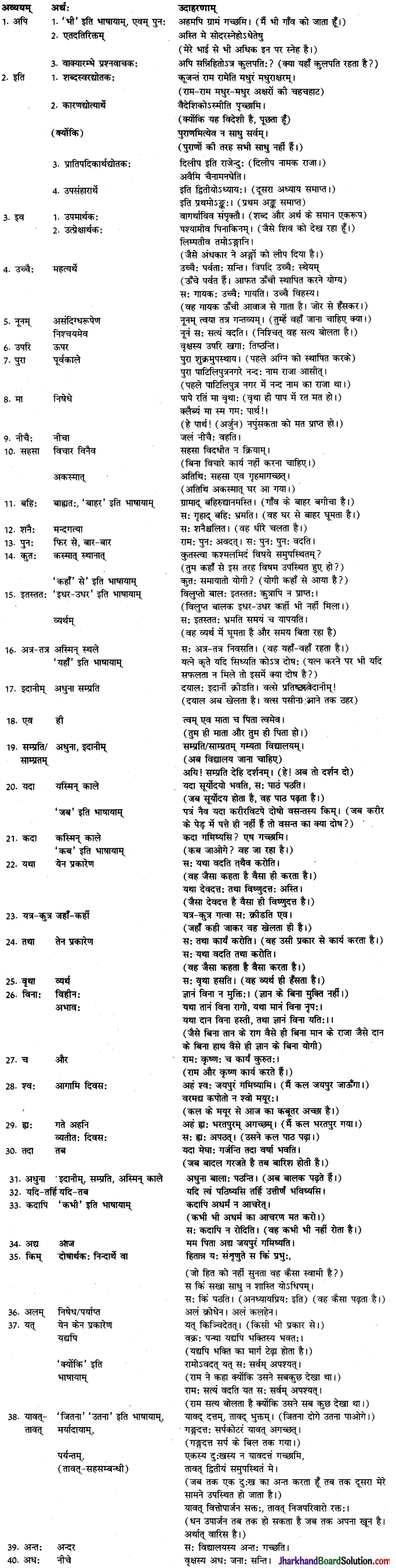
अत्र केषाञ्चिदव्ययानां अर्थोः उदाहरणानि च प्रस्तूयन्ते- (यहाँ कुछ अव्ययों के अर्थ और उदाहरण प्रस्तुत किये जा ‘ रहे हैं-)
ध्यातव्यम् –
अव्ययानां पञ्च भेदा सन्ति (अव्ययों के पाँच भेद हैं-)
(i) क्रिया-विशेषण
(ii) सम्बन्धबोधक
(iii) समुच्चयबोधकः
(iv) विस्मयादिबोधकः
(v) उपसर्गाः।
1. क्रिया-विशेषण अव्यय – जो अव्यय शब्द क्रिया की विशेषता बतलाते हैं, उन्हें क्रिया-विशेषण अव्यय कहा जाता है। इन्हें मुख्यतः तीन भागों में विभाजित किया जा सकता है – (i) कालवाचक (ii) स्थानवाचक (ii) रीतिवाचक (iii) रीतिवाचक क्रियाविशेषण।
2. सम्बन्धबोधक अव्यय – जो अव्यय शब्द संज्ञा, सर्वनाम आदि शब्दों के सम्बन्ध का बोध कराते हैं, उन्हें सम्बन्धबोधक अव्यय कहते हैं। यथा
(i) नगरस्य मध्ये एव चिकित्सालयः अस्ति। (नगर के मध्य ही चिकित्सालय है।)
(ii) ग्रामस्य समीपे एव नदी प्रवहति। (गाँव के समीप ही नदी बहती है।) यहाँ ‘मध्ये’ और ‘समीपे’ सम्बन्धबोधक अव्यय हैं।

3. समुच्चयबोधक अव्यय-जो अव्यय शब्द दो पदों या वाक्यों को परस्पर जोड़ने का काम करते हैं, उन्हें समुच्चय– बोधक अव्यय कहते हैं। जैसे-च (और) वा (अथवा) आदि।
(i) सुरभितः शीतलः च पवन: वहति। (सुगन्धित और शीतल हवा चल रही है।)
(i) महेशः दिनेशः वा गायति। (महेश अथवा दिनेश गा रहा है।)
4. विस्मयादिबोधक अव्यय-जो अव्यय शब्द हर्ष, विषाद, सम्बोधन, दुःख, खेद, घृणा, आश्चर्य, आशीर्वाद, भय, लज्जा आदि भावों या मनोविकारों को प्रकट करते हैं, उन्हें विस्मयादिबोधक या मनोविकारसूचक अव्यय कहते हैं, जैसे –
आः, अहो, आम्, अहह, धिक्, हा, हन्त आदि।
(i) आ:! स्वयं मृतोऽसि। (अरे! स्वयं मर गये हो।)
(ii) अहो ! देशस्य दुर्भाग्यम्। (अरे! देश का दुर्भाग्य।)
(iii) अहो ! बलीयः खलु भीतोऽस्मि। (अरे ! बहुत अधिक डर गया हूँ।)।
5. उपसर्ग अव्यय-उपसर्ग वे अव्यय शब्दांश हैं जो क्रियादि पदों से पूर्व जुड़कर उनके अर्थ को बदल देते हैं या उसमें कुछ विशेषता ला देते हैं। ये प्र आदि 22 होते हैं अत: इन्हें ‘प्रादयः’ कहते हैं। इनका अपना कोई अर्थ या स्वतन्त्र प्रयोग नहीं होता। ये हैं – प्र (अधिक), परा (पीछे), अप (दूर), सम् (अच्छी तरह), अनु (पीछे), अव (दूर, नीचे), निस् (बिना), निर् (बाहर), दुस् (कठिन), दुर् (बुरा), वि (बिना), आङ् (तक), नि (नीचे), अधि (ऊपर), अपि (भी), अति (बहुत), सु (अच्छा), उद् (ऊपर), अभि (ओर), प्रति (ओर, उल्टा), परि (चारों ओर), उप (निकट)। यथा – प्रणामः, पराजयः, अपमानः, संयोगः, अनुरागः, अवमानना, निस्सन्देहः, निराकारः, दुस्साहसः, दुर्जयः, वियोगः, आवासः, निरोधः, अधिकारः, अपिधानम् (पिधानम्), अतिक्रमणम्, सुभगः, उत्थानम्, अभिमानम्, प्रत्युत्तरम्, परितः, उपयोगः।
नोट – उपर्युक्त स्थूलांकित शब्दांश उपसर्ग हैं।
अभ्यासः
प्रश्न 1.
अधोलिखित प्रश्नानाम् उचित विकल्पं चित्वा लिखत –
1. ……………. स्वर्णमयी लङ्का लक्ष्मण मे न रोचते।
(अ) अपि
(ब) इति
(स) इव
(द) एव
उत्तरम् :
(अ) अपि

2. तस्य स्वत्वं. ……….. राष्ट्रे भवितुं न किलार्हति।
(अ) तु
(ब) तत्र
(स) कुत्र
(द) यत्र।
उत्तरम् :
(ब) तत्र
3. स्थाने खलु ऋषिजनेन सर्वदमन ……………. कृतनामधेयोऽसि।
(अ) अपि
(ब) इति
(स) यत्
(द) तत्र
उत्तरम् :
(ब) इति
4. ……………. वा मम माता?
(अ) तत्र
(ब) कुत्र
(स) तत्र
(द) यत्
उत्तरम् :
(ब) कुत्र
5. प्रतापस्य राज्ये ………….. जनक्षतिः धनक्षति च सजाता।
(अ) एवं
(ब) यत्
(स) अपि
(द) इति
उत्तरम् :
(स) अपि

6. ……………. तु मातुः सहयोगाय वीरमा गोचारण कार्यमारभत।
(अ) इदानीम्
(ब) अत्र
(स) इति
(द) एन
उत्तरम् :
(अ) इदानीम्
7. अयं पुनः गण्डस्योपरि पिटकः संवृत्तः…………….भयङ्करो दुर्भिक्षकालः समापन्नः।
(अ) इति
(ब) अपि
(स) यत्
(द) एव
उत्तरम् :
(स) यत्
8. ……………. केनापि कृपालना अनाथालये प्रवेशितः।
(अ) यत्र
(ब) तत्र
(स) अत्र
(द) कुत्र
उत्तरम् :
(ब) तत्र
9. ……………. तस्य हृदि संस्कृताध्ययनेच्छा।
(अ) तत्र
(ब) यत्र
(स) अत्र
(द) अपि
उत्तरम् :
(स) अत्र

10. जिज्ञासे सति कथितं ……………. जाटस्य तव संस्कृतं क्व सुलभम्?
(अ) यतः
(ब) यत्
(ब) चेत्।
(स) इति
उत्तरम् :
(अ) यतः
प्रश्न 2.
अधोलिखिताव्ययपदेषु उचितमव्ययपदं चित्वा रिक्त-स्थानं पूरयत।
(निम्न अव्यय पदों में से उचित अव्यय चुनकर रिक्त-स्थान की पूर्ति कीजिए।)
(क) शिखराणि ……………… लताभिः पुष्पिताग्रामिरूपगूढानि। (पुरुतः/सर्वतः)
(ख) वीरो …………….गर्वित कुञ्जस्थः। (तथा/यथा)
(ग) बोधिसत्वः …………. कस्मिंश्चित् सरसि मत्स्याधिपतिः बभूव। (किल/खलु)
(घ) वर्षनिवृत्ति साशङ्कः …………….. पर्जन्यमाबभाषे। (मुहुर्मुहुः पुनः पुनः)
(ङ) तवैव …………….. एषः सत्यातिशयप्रभावः। (किल/खलु)
(च) सः नैव स्त्री न …………. पुमान्। (ततः/पुनः)
(छ) हा ……………… ! अयमपि नाम परसम्पत्त्या सन्तप्यते ? (धिक्/हन्त)
(ज) हम्मीरदेवेन ……………… युद्धं कृतवान्। (साकं/प्रति)
(झ) महिमासाहिना ………….. त्वामनतकपरं नेष्यामि। (पुर:/सद्)
(ब) ………… परश्वोः वा दुर्गं ग्राहमिषवः। (ह्य/श्व:)
(ट) यवनराजेन ……………… योत्स्यामि। (सम/प्रति)
(ठ) यूयं सर्वे दुर्गाद् …………….. स्थानान्तरं गच्छत। (अन्तः/बहिः)
(ड) ………………… अलावरीनो नाम यवनराजो बभूव। (कुत्र/तत्र)
(ढ) पलायनमयि नोचितं (ततः/यतः)
(ण) नो चेदितो ………………. गच्छामि। (यत्र/अन्यत्र)
(त) यवनराजेन हम्मीरदेवं ………… दूतः प्रहितः। (प्रति/यदि)
(थ) …………… एनं न दास्यति तदा श्वस्तने तव दुर्गं विनशिष्यामि। (यदि/तदा)
(द) ………… निर्भसिते दूते गते। (यत:/ततः)
उत्तराणि :
(क) सर्वतः
(ख) यथा
(ग) किल
(घ) पुनः पुनः
(ङ) खलु
(च) पुनः
(छ) धिक्
(ज) साकम्
(झ) सह
(ज) श्वः
(ट) समम्
(ठ) बहिः
(ड) तत्र
(ढ) यतः
(ण) अन्यत्र
(त) प्रति
(थ) यदि
(द) ततः।

प्रश्न 3.
उचितेन अव्ययपदेन रिक्त-स्थानं पूरयत। (उचित अव्यय पद से रिक्त-स्थान की पूर्ति कीजिये।)
(क) मयि जीवति यमः ……………….. त्वां पराभवितुं न शक्नोति।
(ख) हम्मीरदेवेन साकं युद्धं कृतवान् ………………….. जयं न लब्धवान्।
(ग) यद्येनं न दास्यति …………………… श्वस्तने प्रभाते तव दुर्गं नाशयिष्यामि।
(घ) श्वः ………. वा दुर्गं ग्राहयिष्यावः।
(ङ) किञ्च यदि मन्यसे ……. निर्भय स्थानं त्वां प्रापयामि।
(च) ………………. एव क्रीडित्वा सोऽपि समागतः।
(छ) स्वामिन्याः …………………. भविष्यति।
(ज) कियद्वारं निर्दिष्टोऽसि ……………. प्रवचनं न कार्यम्।
(झ) अद्यागत ……………… एव वात्याचक्रमुत्थापयसि।
(ब) तव पिता …………… किं करोति ?
उत्तराणि :
(क) अपि
(ख) परं
(ग) तदा
(घ) परश्वः
(ङ) तदा
(च) इदानीम्
(छ) पार्वे
(ज) यत्
(झ) प्राय
(ब) च।
प्रश्न 4.
मञ्जूषायां प्रदत्तैः अव्ययपदैः रिक्तस्थानानि पूरयित्वा उत्तरपुस्तिकायां लिखत –
(मञ्जूषा में दिये हुए अव्यय पदों से रिक्त-स्थानों की पूर्ति करके उत्तर-पुस्तिका में लिखिए -)
1. तावत्, यत्र, तत्र, यदा, श्वः ह्यः, पुरा
(क) ह्यः सोमवासरः आसीत …………… बधवासरः भविष्यति।
(ख) …………. त्वम् आगमिष्यसि तदा अहम् आगमिष्यामि।।
(ग) यावत् त्वम् अत्र स्थास्यसि : ……………………… अहम् न आगमिष्यामि।
उत्तराणि :
(क) ह्यः सोमवासरः आसीत्, श्वः बुधवासरः भविष्यति।
(ख) यदा त्वम् आगमिष्यसि तदा अहम् आगमिष्यामि।
(ग) यावत् त्वम् अत्र स्थास्यसि तावत् अहं न आगमिष्यामि।

2. विना, सह, नूनम्, यदा, अधुना, अत्र, तत्र ।
रामः – अहं त्वां (i) …………. न गमिष्यामि।
मोहनः – किमर्थं मया एव (ii) …………. गमिष्यसि ?
रामः – (iii) ………….. रात्रिः अस्ति। अहम् अंधकारात् त्रस्यामि।
उत्तराणि :
रामः – अहं त्वां विना न गमिष्यामि।
मोहनः – किमर्थं मया एव सह गमिष्यसि ?
रामः – अधुना रात्रिः अस्ति। अहम् अंधकारात् त्रस्यामि।
3. किमर्थम्, तत्र, बहिर्, अधुना; इतस्ततः, कुतः, यत्।
नैतिक – गर्वित ! गृहाद् (i) ………… गत्वा उद्यानात् पुष्पाणि आनय।
गर्वित – भ्रातः ! अहं (i) ………… एकाकी न गमिष्यामि।
नैतिक – (iii) …………. एकाकी न गमिष्यसि।
उत्तराणि :
नैतिक – गर्वित ! गृहाद बहिर् गत्वा उद्यानात् पुष्पाणि आनय।
गर्वित – भ्रातः! अहं तत्र एकाकी न गमिष्यामि।
नैतिक – किमर्थम् एकाकी न गमिष्यसि ?
4. अन्यत्र, अपि, कुत्र, किमर्थम्, तदा, यदा, मा।
सीमा – सुरेखे! त्वं प्रभाते (i) ………… गच्छसि?
सुरेखा – अहं (ii) ………… भ्रमितुं गच्छामि।
सीमा – तिष्ठ, अहम् (iii) …………… त्वया सह चलिष्यामि।
उत्तराणि :
सीमा – सुरेखे! त्वं प्रभाते कुत्र गच्छसि ?
सुरेखा – अहं अन्यत्र भ्रमितुं गच्छामि।
सीमा – तिष्ठ, अहम् अपि त्वया सह चलिष्यामि।

5. तत्र, श्वः, ह्यः, कुत्र, यत्र, शनैः शनैः, इतस्ततः
राम – श्याम! सुनील: (i) …………… गतः ?
श्याम – (ii) …………. अहं तम् आपणे अपश्यम्।
राम – सः (iii) ………….. किं करोति स्म ?
उत्तराणि :
राम – श्याम! सुनील: कुत्र गतः ?
श्याम – ह्यः अहं तम् आपणे अपश्यम्।
राम – सः तत्र किं करोति स्म ?
6. इतस्ततः, मा, तावत्, बहिः, सहसा, यदा, तदा।।
(i) यावत् अहम् अत्र तिष्ठामि …………. मा गच्छ।
(ii) सिंहस्य अभावे वने जीवाः …………… भ्रमन्ति।
(iii) ………….. कदापि कार्याणि न कुर्यात्।
उत्तराणि :
(i) यावत् अहम् अत्र तिष्ठामि तावत् मा गच्छ।
(ii) सिंहस्य अभावे वने जीवाः इतस्ततः भ्रमन्ति।
(iii) सहसा कदापि कार्याणि न कुर्यात्।
7. एव, अलम्, उच्चैः, अधुना, शनैः, च, अपि।
अनिलः – आगतः अस्मि, श्रीमन्त: (i) ………… किं करवाणि ?
अध्यापकः – (ii) ………..” भ्रमणेन। अत्र उपविश।
अनिल: – आम्, उपविशामि। यद् भवन्तः कथयिष्यन्ति तद् (iii) ……….. …. करिष्यामि।
उत्तराणि :
अनिलः – आगतः अस्मि, श्रीमन्तः अधुना किं करवाणि ?
अध्यापकः – अलं भ्रमणेन। अत्र उपविश।
अनिलः – आम्, उपविशामि। यद् भवन्तः कथयिष्यन्ति तद् एव करिष्यामि।
8. अपि, पुरा, विना, बहिः, कुत्र, वृथा, शनैः।
भानुप्रिया – त्वम् अधुना (i) …………… गच्छसि ?
भानुप्रताप – अहं ग्रामाद (ii) …………… भ्रमणाय गच्छमि।
भानुप्रिया – अहम् (iii) …………. त्वया सह गन्तुम् इच्छामि।
उत्तराणि :
(i) कुत्र
(ii) बहिः
(iii) अपि

9. बहिः, एव, अपि, कुत्र, यत्र, तत्र, किमर्थम्।
माता – वत्स! एषः कोलाहलः (i) …………. भवति।
पुत्रः – मातः! (ii) …………… एकः अहितुण्डकः आयातः।
माता – एते अहितुण्डकाः सर्पान् (iii) ………….. प्रदर्शयन्ति।
उत्तराणि :
माता – वत्स ! एषः कोलाहलः कुत्र भवति।
पुत्रः – माता:! बहिर् एकः अहितुण्डकः आयातः।
माता – एते अहितुण्डकाः सर्पान् किमर्थं प्रदर्शयन्ति ?
10. ननु, नूनम्, एव, श्वः, अपि, खलु, तत्र
शिक्षकः – छात्राः! (i) …………. विद्यालये वृक्षारोपणं भविष्यति।
मोहनः – अहं गृहाद् (ii) …………… एकं पादपम् आनेष्यामि।
शिक्षकः – निर्मले! त्वम् (iii) …………… पादपम् आनेष्यति।
उत्तराणि :
शिक्षकः – छात्राः! श्वः विद्यालये वृक्षारोपणं भविष्यति।
मोहनः – अहं गृहाद् एव एक पादपम् आनेष्यामि।
शिक्षकः – निर्मले ! त्वम् अपि पादपम् आनेष्यति।
11. शनैः शनैः, इतस्ततः, तथा, यदा, यदि, अत्र, अपि।
अपूर्वः – (i) …………. एकं विशालम् उपवनम् अस्ति।
प्रत्यूषः – पश्य, वृक्षेषु वानराः (ii) ………… कूर्दन्ति।
अपूर्वः – तत्र तु मयूरा: (iii) …………… नृत्यन्ति।
उत्तराणि :
अपूर्वः – अत्र एक विशालम् उपवनम् अस्ति।
प्रत्यूषः – पश्य, वृक्षेषु वानराः इतस्ततः कूर्दन्ति।
प्रत्यूषः – तत्र तु मयूराः अपि नृत्यन्ति।

12. यथा, अलम्, इदानीम्, इतः
शिक्षकः – सचिन ! (i) …………..” आगच्छ।
सचिन – आगतः श्रीमन् (i) ………….. किं करणीयम्। भ्रमणाय गच्छामि।
शिक्षकः – (iii) ………… भ्रमणेन, पाठं स्मर।
उत्तराणि :
शिक्षकः – सचिन! इतः आगच्छ।
सचिन – आगतः श्रीमन् ! इदानीं किं करणीयम्। भ्रमणाय गच्छामि।
शिक्षक – अलं भ्रमणेन पाठं स्मर।
13. उच्चैः, अधुना, अद्य, ह्यः, बहिः, श्वः, तदा।
(क) विद्यालये ……….. वार्षिकोत्सवः अस्ति।
(ख) छात्राः विद्यालयात् ………… प्रवेशद्वारे अतिथीनां स्वागतं करिष्यन्ति।
(ग) केचन …………… जयघोषं करिष्यन्ति।
उत्तराणि :
(क) विद्यालये अध वार्षिकोत्सवः अस्ति।
(ख) छात्राः विद्यालयात् बहिः प्रवेशद्वारे अतिथीनां स्वागतं करिष्यन्ति।
(ग) केचन उच्चैः जयघोषं करिष्यन्ति।
14. ह्यः, मा, यत्र, विना, श्वः, अपि, एव।
(क) बालाः ……………… क्रीडन्ति, तत्र जनाः अपि भ्रमन्ति।
(ख) परिश्रमं ……………….. कुत्र साफल्यम् ?
(ग) भवन्तः ……………….. किमर्थं गमिष्यन्ति ?
उत्तराणि :
(क) बालाः यत्र क्रीडन्ति, तत्र जनाः अपि भ्रमन्ति।
(ख) परिश्रमं विना कुत्र साफल्यम् ?
(ग) भवन्तः श्वः किमर्थं गमिष्यन्ति ?

15. पुनः, इति, अपि, विना, ह्यः, इतस्ततः, उच्चैः।
(i) ………..” वयं जन्तुशालां द्रष्टुं काननवनम् अगच्छाम। सर्वे पशवः (i) ……………. भ्रमन्ति स्म। सिंहाः (ii) …………. गर्जन्ति स्म।
उत्तराणि :
ह्यः वयं जन्तुशालां द्रष्टुं काननवनम् अगच्छाम। सर्वे पशवः इतस्ततः भ्रमन्ति स्म। सिंहाः उच्चैः गर्जन्ति स्म।
16. विना, पुनः, एव, तत्र-तत्र, इति, शनैः, अतः
वस्तुत: मयूरं (i) …………. कुत्र जन्तुशालायाः शोभा। तत्र आम्रवृक्षाः आसन् (i) …………. कोकिलाः अपि आसन्। यत्र-यत्र आम्रवृक्षाः (iii) ………….. कोकिला: तु भविष्यन्ति एव।
उत्तराणि :
वस्तुत: मयूरं विना कुत्र जन्तुशालायाः शोभा। तत्र आम्रवृक्षाः आसन् अतः कोकिलाः अपि आसन्। यत्र-यत्र आम्रवृक्षाः तत्र-तत्र कोकिला: तु भविष्यन्ति एव।
17. अधुना, सदैव, वृथा, एव, यत्र-यत्र, इव, नूनम्।।
ते जनाः (i) ……….. धन्याः, ये कदापि निरुत्साहिताः न भवन्ति। ते सदैव धन्याः, ये (ii) …………. न …………. वदन्ति। ते (iii) …………… गच्छन्ति, तत्र-तत्र सफलाः भवन्ति।
उत्तराणि :
ते जनाः नूनं धन्याः, ये कदापि निरुत्साहिताः न भवन्ति। ते सदैव धन्याः, ये वृथा न वदन्ति। ते यत्र-यत्र गच्छन्ति, तत्र-तत्र सफलाः भवन्ति।

18. सह, उच्चैः, बहिः, इतस्ततः, अपि, एव, शीघ्रम्।
नगरात् (i) ………….. एकं वनम् अस्ति। तत्र दिने (ii) …………… अन्धकारः भवति। जनाः प्रायः कुक्कुरैः (iii) ……….. एव तत्र प्रविशन्ति।
उत्तराणि :
नगरात् बहिर् एकं वनम् अस्ति। तत्र दिने अपि अन्धकारः भवति। जनाः प्रायः कुक्कुरैः सह एव तत्र प्रविशन्ति।
19. इतस्ततः, तत्र, परम्, विना, तु, ह्यः सदैव।
(i) ………….. वयं बुद्धोद्याने भ्रमितुम् अगच्छाम। जनाः तत्र (ii) …………… भ्रमन्ति स्म। (iii) …………… छात्राः पुस्तकानि अपठन्।
उत्तराणि :
ह्यः वयं बुद्धोद्याने भ्रमितुम् अगच्छाम। जनाः तत्र इतस्ततः भ्रमन्ति स्म। तत्र छात्राः पुस्तकानि अपठन्।
20. मा, इतस्ततः, उपरि, अधः, अद्य, विना, सर्वत्र।
(i) ………….. वने पशु महोत्सवः अस्ति। मञ्चस्य (ii) …………… वनराजः सिंहः तिष्ठति। आकाशे (iii) …………. मेघाः सन्ति।
उत्तराणि :
अद्य वने पशु महोत्सवः अस्ति। मञ्चस्य उपरि वनराजः सिंह: तिष्ठति। आकाशे सर्वत्र मेघाः सन्ति।
21. सहसा, उच्चै, एव, पुरा।
(i) …………. गायति सः गायकः। (ii) सदा सत्यम् विजयति। (iii) ………….. संस्कृतं जनभाषा आसीत्।
उत्तराणि :
(i) उच्चै। (ii) एव। (iii) पुरा।
22. बहिः, अपि, यथा, कुत्र।
(i) सः क्रीडति अहम् …………… क्रीडामि। (i) भवती …………… पठति। (iii) ………. गुरुः तथा शिष्यः।
उत्तराणि :
(i) अपि। (ii) कुत्र। (iii) यथा।

23. एव, सहसा, वृथा, बिना।
(i) ……….. विदधीत न क्रियाम्। (ii) क्रियां ………… नरः अकर्मण्यः भवति। (iii) कर्मणा …………. नरः पूज्यते।
उत्तराणि :
(i) सहसा। (ii) बिना। (iii) एव।
प्रश्न 5.
अधोलिखितानाम् अव्यय शब्दानां स्वरचित संस्कृत वाक्येषु प्रयोगं कुरुत।
(निम्नलिखित अव्यय शब्दों का स्वरचित संस्कृत वाक्यों में प्रयोग कीजिए।)
उच्चैः, शनैः, अधः, अद्य, ह्यः, सायं, चिरम्, ईषत्, तूष्णीम् सहसा, पुरा, नूनम्, भूयः, खलु, धिक्।
उत्तर :
- बालकः दृश्यम् अवलोक्य उच्चैः हसति। (बालक दृश्य को देखकर जोर से हँसता है।)
- कच्छपः शनैः शनैः चलति। (कछुआ धीरे-धीरे चलता है।)
- वृक्षस्य अधः एव साधोः उटजम्। (वृक्ष के नीचे ही साधु की कुटिया है।)
- अद्य अहं विद्यालयं न गमिष्यामि। (आज मैं विद्यालय नहीं जाऊँगा।)
- ह्यः सत्यदेवः जयपुरम् अगच्छत्। (कल सत्यदेव जयपुर गया।)
- सायंकाले खगाः स्व स्व नीडं प्रत्यागच्छन्ति। (सायंकाल पक्षी अपने-अपने घोंसले में आ जाते हैं।)
- चिरं जीवतु रामः। (रमा चिरायु हों)
- मह्यम् ईषद् जलं देहि। (मुझे थोड़ा जल दो।)
- तूष्णीं भव नोचेदाचार्य निवेदयिष्यामि। (चुप हो जा नहीं तो आचार्य से कह दूँगा।)
- सहसैव सः तत्र प्राप्तः। (अकस्मात् ही वह वहाँ पहुँच गया।)
- पुरा आदिकविः वाल्मीकिः रामचरितमलिखत्। (पहले आदिकवि वाल्मीकि ने रामचरित लिखा।)
- अद्य सः नूनम् आगमिष्यति। (आज वह अवश्य आयेगा।)
- भूयो भूयः नमाम्यहम्। (मैं बार-बार नमस्कार करता हूँ।)
- नीचैः विघ्न भयेन खलु न प्रारभ्यते। (नीच (अधम) लोगों द्वारा विघ्नों के भय के कारण निश्चय ही कार्य प्रारम्भ नहीं किया जाता है।)
- धिक् मूर्खम्। (मूर्ख को धिक्कार है)

प्रश्न 6.
अधोलिखिताव्ययानामर्थं हिन्दीभाषायां लिखित्वा संस्कृत वाक्येषु प्रयोगं कुरुत।
(निम्न अव्ययों का हिन्दी में अर्थ लिखकर संस्कृत वाक्यों में प्रयोग कीजिए।
तथा, नीचैः, युगपत, मिथ्या, श्वः, अचिरम, पार्वे, किल, यत्र, यत्।
उत्तराणि :
- तथा – (वैसा) यथा मेघाः गर्जन्ति तथा एव जलं वर्षति। (जैसे मेघ गर्जते हैं वैसे ही जल बरसता है।)
- नीचैः – (धीमे) त्वं सर्वदा नीचैः एव वदसि। (तम हमेशा धीमे बोलते हो।)
- युगपत् – (एक साथ) चक्रेण युगपत्। (चक्र के साथ)
- मिथ्या – (झूठ) मिथ्या वचनं पापमूलम्। (मिथ्या वचन पाप का मूल है।)
- श्वः – (आने वाला कल) अहं श्वः एव विदेशं गमिष्यामि। (मैं कल ही विदेश जाऊँगा।)
- अचिरम् – (शीघ्र) अचिरमेव सः अरोदत्। (वह शीघ्र रो पड़ा)
- पार्श्वे – (पास, बगल में) मातुः पार्वे भविष्यति। (माँ के पास होगा।)
- किल – (निश्चय, अवश्य ही) गायन्ति देवाः किल गीतकानि। (निश्चित ही देवता गीत गाते हैं।)
- यत्र – (जहाँ) सः तत्र गच्छति यत्र त्वं गच्छसि। (वह वहाँ जाता है जहाँ तू जाता है।)
- यत् – (कि) अहं जानामि यत् त्वं मूर्योऽसि। (मैं जानता हूँ कि तुम मूर्ख हो)।
![]()
![]()