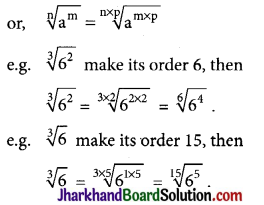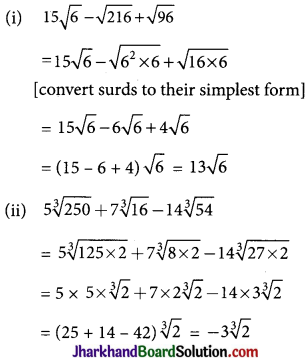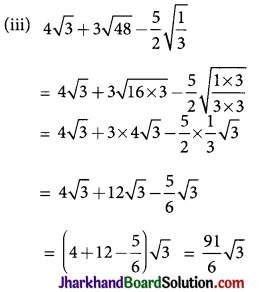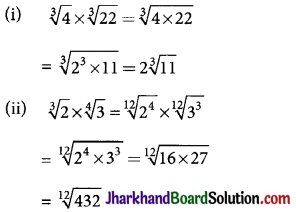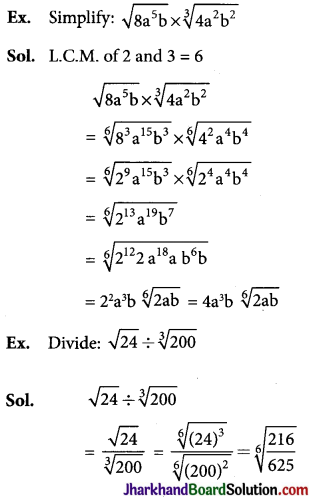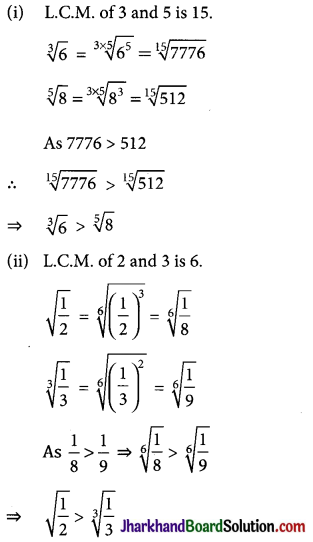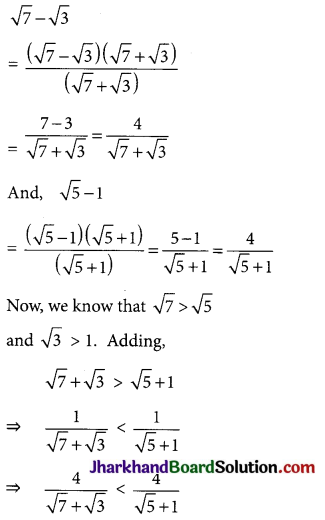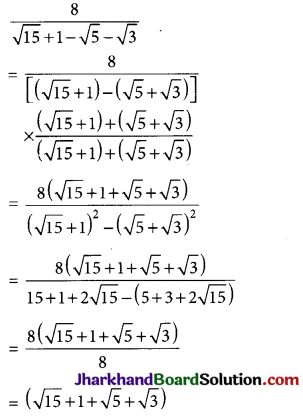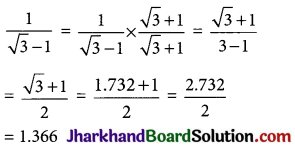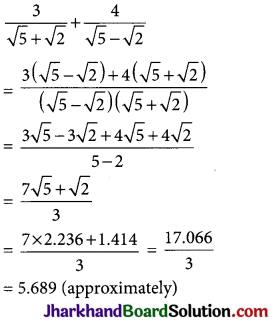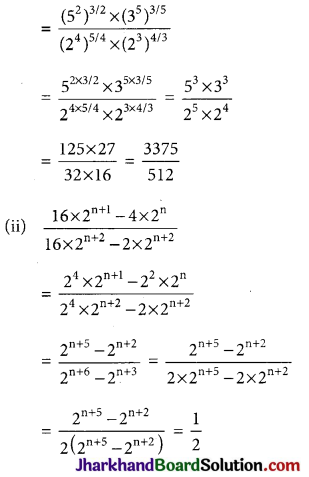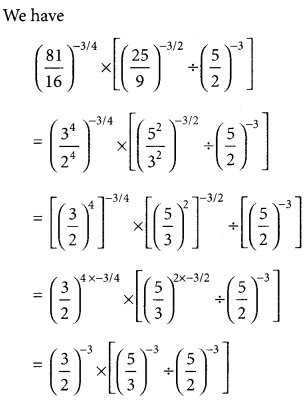Students should go through these JAC Class 9 Maths Notes Chapter 1 Number Systems will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 1 Number Systems
Classification Of Numbers:
→ Natural numbers: The numbers used for counting are called natural numbers. So, the number 1 and any other number obtained by adding 1 to it repeatedly. Hence 1, 2, 3 … represent natural numbers. Set of natural numbers is denoted by N.
→ Whole numbers: Natural numbers along with 0 are termed as whole numbers. So, the smallest whole number is 0. The set of whole numbers is represented by W.
→ Integers: All positive and negative whole numbers that do not include any fractional or decimal parts are called integers. The set of integers is expressed as Z = {……-3, -2, -1, 0, 1, 2, 3, ……}, where Z is the symbol used to denote the set of integers.
→ Rational numbers: These are numbers which can be expressed in the form of p/q, where p and q are integers and q ≠ 0. e.g. 2/3, 37/15, -17/19. The set of rational numbers is represented by the symbol Q.
- All natural numbers, whole numbers and integers are rational numbers.
- Rational numbers include all Integers (without any decimal part to it), terminating decimals (e.g. 0.75, -0.02 etc.) and also non-terminating but recurring decimals (e.g. 0.666…, -2.333…… etc.)
- All fractions are rational numbers but every rational number is not a fraction, Since both numerator and denominator are always positive in a fraction but a rational number can have both numerator and denominator as negative.
Fractions:
→ Common fraction: A common fraction is a fraction in which numerator and denominator are both integers, eg, \(\frac{2}{5}\), \(\frac{1}{2}\) etc.
→ Decimal fraction: Fractions whose denominator is 10 or any power of 10.
→ Proper fraction: It is a fraction whose numerator is smaller than its denominator eg. \(\frac{3}{5}\).
→ Improper fraction: It is a fraction whose numerator is greater than its denominator eg. \(\frac{5}{3}\).
→ Mixed fraction: A combination of a proper fraction and a whole number is called mixed fraction eg. 3\(\frac{2}{7}\) etc. Improper fraction can be written in the form of mixed fractions.
→ Compound fraction: A fraction in which the numerator or the denominator or both contain one or more fractions eg \(\frac{2 / 3}{5 / 7}\).
→ Irrational numbers. These are numbers which cannot be expressed in the form of p/q, where p and q are integers and q≠0. These are non-recurring as well as non-terminating type of decimal numbers eg \(\sqrt{2}\), π, 0.202002000…… etc.
→ Real numbers: Numbers which can represent actual physical quantities in a meaningful way are known as real numbers. These can be represented on the number line Number line is geometrical straight line with arbitrarily defined zero (origin). The set of real number is denoted by the symbol R.
→ Prime numbers: All natural numbers that have one and themselves only as their factors are called prime numbers le prime numbers are divisible by 1 and themselves only e.g. 2 3, 5, 7, 11, 13, 17, 19, 23….etc.
→ Composite numbers: All natural numbers, which has three or more different factors are called composite numbers. E.g. 4, 6, 8, 9, 10, 12,… etc.
- 1 is neither prime nor composite.
→ Co-prime numbers: If the H.C.F. of the given numbers (not necessarily prime) is 1 then they are known as co-prime numbers. e.g. 4, 9 are Co-prime as H.C.F of (4, 9) = 1.
- Any two consecutive integer numbers will always be co-prime.
→ Even numbers: All integers which are divisible by 2 are called even numbers. Even numbers are denoted by the expression 2n, where n is any integer. e.g ….., 4, -2, 0, 2, 4…..
→ Odd numbers: All integers which are not divisible by 2 are called odd numbers. Odd numbers are denoted by the general expression 2n – 1 or 2n + 1, where is any integer. e.g. ……,-5, -3, -1, 1, 3, 5,….

Identification Of Prime Number:
Step 1: Find approximate square root of given number.
Step 2: Divide the given number by prime numbers less than approximate square root of number. If given number is not divisible by any of these prime numbers then the number is prime otherwise not.
Example:
571, is it prime?
Solution:
Approximate square foot of 571 = 24.
Prime number < 24 are 2, 3, 5, 7, 11, 13, 17, 19 and 23. But 571 is not divisible by any of these prime numbers, so 571 is a prime number.
Example:
Is 1 prime or composite number?
Solution:
1 is neither a prime nor a composite number.
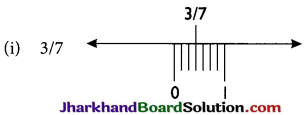
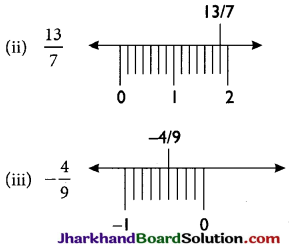
Representation For Rational Number On A Real Number Line:
Divide 0 to 1 into 7 equal parts on real number line.
Note:
- In a positive rational number, if numerator is smaller than its denominator then it lies between 0 and 1 on the number line.
- In a negative rational number if absolute value of numerator less than its denominator then it lies between -1 and 0.
Decimal Number (Terminating):
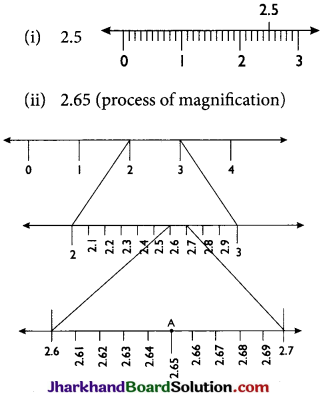
Here, A represents 2.65 on the number line.
Example:
Visualize the representation of \(5.3 \overline{7}\) on the number line upto 5 decimal places. i.e. 5.37777.
Solution:
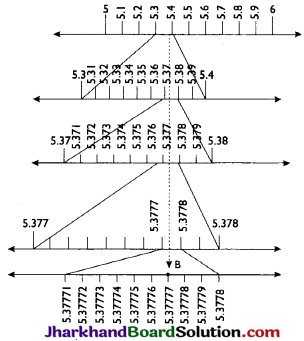
Here, B represents 5.7777 on the number line upto 5 places of decimal.

Rational Number In Decimal Representation:
→ Terminating Decimal:
In this, a finite number of digits occurs after decimal point i.e. 0.5, 0.6875, 0.15 etc.
→ Non-Terminating and Repeating (Recurring) Decimal:
In this a set of digits or a digit is repeated continuously
Ex. \(\frac{2}{3}\) = 0.6666… = \(0 . \overline{6}\)
Ex. \(\frac{1}{2}\) = 0.454545… = \(0 . \overline{45}\).
Properties Of Rational Numbers:
Let a, b, c be three rational numbers.
- Commutative property of addition: a + b = b + a
- Associative property of addition: (a + b) + c = a + (b + c)
- Additive identity: a + 0 = a is called an identity element of a.
- Additive inverse a + (-a) = 0, 0 is identity element, -a is called additive inverse of a.
- Commutative property of multiplications: a.b = b.a
- Associative property of multiplication: (a × b) × c = a × (b × c)
- Multiplicative Identity: 2 × 1 = 2, 1 is called multiplicative identity of a.
- Multiplicative inverse: (a) × (\(\frac{1}{a}\)) = 1. 1 is called multiplicative identity and \(\frac{1}{a}\) is called multiplicative inverse of a or reciprocal of a.
- Distributive property: a × (b + c) = a × b + a × c
Example:
Prove that \(\sqrt{3}-\sqrt{2}\) is an irrational number.
Solution:
Let, \(\sqrt{3}-\sqrt{2}\) = r where r, be a rational number.
Squaring both sides,
(\(\sqrt{3}-\sqrt{2}\))2 = r2
⇒ 3 + 2 – 2\(\sqrt{6}\) = r2
⇒ 5 – 2\(\sqrt{6}\) = r2
⇒ \(\frac{5-r^2}{2}\) = \(\sqrt{6}\)
Here, \(\sqrt{6}\) is an irrational number but \(\frac{5-r^2}{2}\) is a rational number
∴ LH.S. ≠ R.H.S.
Hence, it contradicts our assumption that \(\sqrt{3}-\sqrt{2}\) is a rational number.
Therefore, \(\sqrt{3}-\sqrt{2}\) is an irrational number.
Irrational Numbers:
These are real numbers which cannot be expressed in the form of p/q, where p and q are integers and q ≠ 0.
→ Irrational Number in Decimal Form:
\(\sqrt{2}\) = 1.414213..ie. it is non-recurring as well as non-terminating
\(\sqrt{3}\) = 1.732050807….. i.e. It is non-recurring as well as non-terminating.
Example:
Insert an irrational number between 2 and 3.
Solution:
\(\sqrt{2 \times 3}=\sqrt{6}\) is an irrational number between 2 and 3.
→ Irrational Numbers on a Number Line:
Example:
Plot \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{5}\), \(\sqrt{6}\) on the same number line.
Solution:
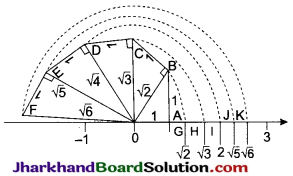
→ Properties of Irrational Numbers:
- Negative of an irrational number is an irrational number eg. \(\sqrt{3}\) and –\(\sqrt{3}\) are irrational numbers.
- Sum and difference of a rational and an irrational number is always an irrational number.
- Sum and difference of two irrational numbers is either rational or irrational number.
- Product of a rational number with an irrational number is either rational or irrational number.
- Product of an irrational with an irrational is not always irrational.
Ex. Two numbers are 2 and \(\sqrt{3}\). then Sum = 2 + \(\sqrt{3}\), is an irrational number Difference = 2 – \(\sqrt{3}\) is an irrational number
Also \(\sqrt{3}\) – 2 is an irrational number.
Ex. Two numbers are 4 and \(\sqrt[3]{3}\), then Sum = 4 + \(\sqrt[3]{3}\), is an irrational number. Difference = 4 – \(\sqrt[3]{3}\), is an irrational number.
Ex. Two irrational numbers are 13, –\(\sqrt{3}\), then
Sum = \(\sqrt{3}\) + (-\(\sqrt{3}\)) = 0, which is rational.
Difference = \(\sqrt{3}\) – (-\(\sqrt{3}\)) = 2\(\sqrt{3}\), which is irrational.

Geometrical Representation Of Irrational Numbers On The Number Line
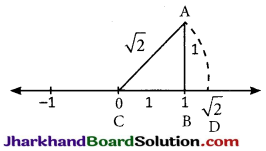
To represent \(\sqrt{2}\) on number line we follow the following steps:
Step I: Draw a number line and mark the centre point as zero.
Step II: Mark right side of the zero as (1) and the left side as (-1).
Step III: We won’t be considering (-1) for our purpose.
Step IV: With same length as between 0 and 1, draw a line perpendicular to point (1), such that new line has a length of 1 unit.
Step V: Now join the point (0) and the end of new line of unit length.
Step VI: A right angled triangle is constructed.
Step VII: Now let us name the triangle as ABC such that AB is the beight (perpendicular), BC is the base of triangle and AC is the hypotenuse of the right angled triangle ABC.
Step VIII: Now length of hypotenuse, i.e., AC can be found by applying pythagoras theorem to the right triangle ABC.
AC2 = AB2 + BC2
⇒ AC2 = 12 + 12
⇒ AC2 = 2
⇒ AC = \(\sqrt{2}\)
Step IX: Now with AC as radius and C as the centre cut an arc on the same number line and name the point as D.
Step X: Since AC is the radius of the arc and hence, CD will also be the radius of the arc whose length is \(\sqrt{2}\).
Step XI: Hence, D is the representation of \(\sqrt{2}\) on the number line.
Surds:
Any irrational number of the form \(\sqrt[n]{a}\) is given a special name surd, where is called radicand it should always be a positive rational number. Also the symbol \(\sqrt[n]{ }\) is called the radical sign and the index n is called order of the surd.
\(\sqrt[n]{a}\) is read as ‘nth root d’ and can also be written as an \(\mathrm{a}^{\frac{1}{n}}\)
→ Some Identical Surds:
- \(\sqrt[3]{4}\) is a surd as radicand is a rational number.
Similar examples \(\sqrt[3]{5}, \sqrt[4]{12}, \sqrt[5]{7}, \sqrt{12} . .\) - 2 + 2\(\sqrt{3}\) is a surd (as rational + surd number will give a surd)
Similar examples: \(\sqrt{3}+1, \sqrt[3]{3}+1, \ldots\) - \(\sqrt{7-4 \sqrt{3}}\) is a surd as 7-4\(\sqrt{3}\) is a perfect square of (2 – \(\sqrt{3}\)).
Similar examples: \(\sqrt{7+4 \sqrt{3}}, \sqrt{9-4 \sqrt{5}}, \sqrt{9+4 \sqrt{5}}, \ldots\) - \(\sqrt[3]{\sqrt{3}}\) is a surd as \(\sqrt[3]{\sqrt{3}}=\left(3^{\frac{1}{2}}\right)^{\frac{1}{3}}\)
= \(3^{\frac{1}{6}}=\sqrt[6]{3}\)
Similar examples : \(15 \sqrt{6}-\sqrt{216}+\sqrt{96}\)
→ Some Expressions are not Surds:
- \(\sqrt[3]{8}\) is not a surd because \(\sqrt[3]{8}=\sqrt[3]{2^3}\) = 2. which is a rational number.
- \(\sqrt{2+\sqrt{3}}\) is not a surd because 2 + \(\sqrt{3}\) is not a perfect square.
- \(\sqrt[3]{1+\sqrt{3}}\) is not a surd because radicand is an irrational number.
Laws Of Surds:

[Important for changing order of surds]
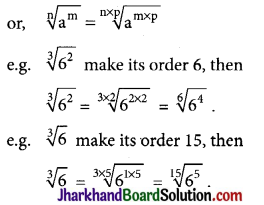

Operation Of Surds:
→ Addition and Subtraction of Surds: Addition and subtraction of surds are possible only when order and radicand are same i.e. only for surds.
Example: Simplify
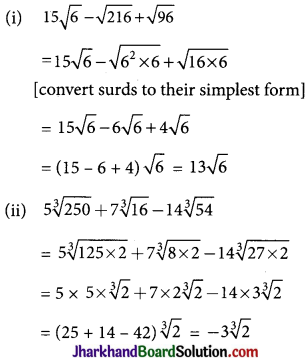
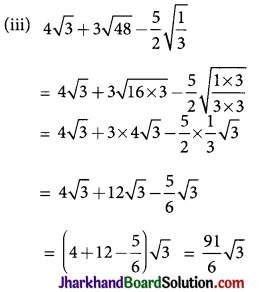
→ Multiplication and Division of Surds:
Example:
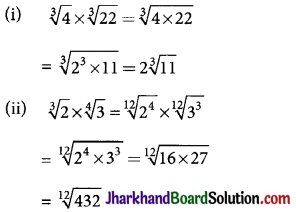
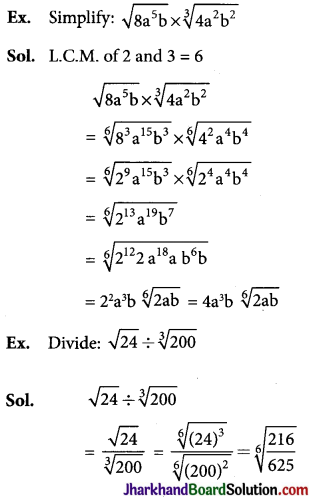
→ Comparison of Surds: It is clear that if x > y > 0 and n > 1 is a positive integer then \(\sqrt[n]{x}>\sqrt[n]{y}\).
Example:
Which is greater in each of the following:
(i) \(\sqrt[3]{6} \text { and } \sqrt[5]{8}\)
(ii) \(\sqrt{\frac{1}{2}} \text { and } \sqrt[3]{\frac{1}{3}}\)
Solution:
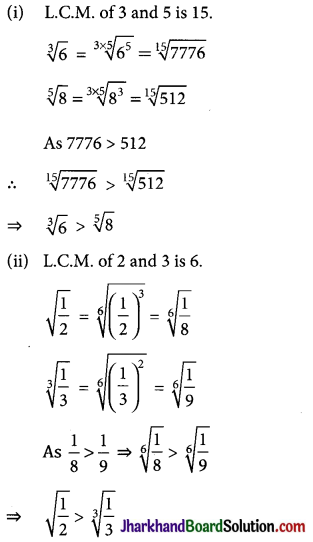
Exponents Of Real Number:
→ Positive Integral Power: For any real number a and a positive integer ‘n’ we define: an = a × a × a × … × a (n times).
an is called nth power of a. The real number ‘a’ is called the base and ‘n’ is called power of a.
e.g. 23 = 2 × 2 × 2 = 8
Note: For any non-zero real number ‘a’ we define a0 = 1.
e.g, thus 30 = 1, 50 = 1, \(\left(\frac{3}{4}\right)^0\) = 1 and so on.
→ Negative Integral Power: For any non-zero real number ‘a’ and a positive integer ‘n’ we define \(a^{-\mathrm{n}}=\frac{1}{a^n}\).

Rational Exponents Of A Real Number:
→ Principal nth Root of a Positive Real Number: If ‘a’ is a positive real number and ‘n’ is a positive integer, then the principal nth root of a is the unique positive real number x such that xn = a.
The principal root of a positive real number a1/n denoted by \(\sqrt[n]{a}\).
→ Principal nth Root of a Negative Real Number: If ‘a’ is a negative real number and ‘n’ is an odd positive integer, then the principal nth root of a is define as \(-|\mathrm{a}|^{1 / \mathrm{n}}\) i.e. the principal nth root of -a is negative of the principal nth root of |a|.
Remark: If ‘a’ is negative real number and ‘n’ is an even positive integer, then the principal nth root of a is not defined, because an even power of real number is always positive. Therefore, (-9)1/2 is a meaningless quantity, if we confine ourselves to the set of real numbers only.
→ Rational Power (Exponents): For any positive real number ‘a’ and a rational number \(\frac{p}{q}\) where q ≠ 0, p, q ∈ Z. We define ap/q = (ap)1/q i.e. ap/qis the principal qth root of ap.
Laws Of Rational Exponents:
The following laws hold for the rational exponents


where a, b are positive real numbers and m, n are rational numbers.